基于RNN-LSTM 的船舶位置预测分析∗

张玉人 龚志猛

（1.中国科学院福建物质结构研究所 福州 350608）（2.华信咨询设计研究院有限公司 杭州 310052）

1 引言

船舶在开阔的航道区间内航行时，很难用一个确定的线性关系去描述船舶的运动情况。通常，研究人员采用马尔科夫过程来建立船舶航行轨迹预测非线性系统模型，但该模型结合轨迹数据建立多特征模型的复杂度较高，也无法记忆较长历史时间跨度的信息［1］。而神经网络通过模拟人脑的神经网络基本结构进行自主学习与训练，能够较好地完成非线性数据的处理工作，具有优异的非线性拟合能力。船舶航行过程中，由于GPS设备采集到的数据具有时序性，而且地理位置之间存在着上下文关联，使得循环神经网络（RNN）应用成为可能。利用RNN 学习当前环境和既有时刻基础上的船舶运动规律，然后进行航迹预测。这既避免了传统算法中繁杂的建模过程，又保证了所建立的模型符合实际逻辑。一个完善的RNN 模型可以预测任意复杂、期望的序列，但标准的循环神经网络模型不能存储过多的历史信息［2～3］。在一定的历史时间跨度下，历史记忆的长短关乎模型预测的准确度。基于上述考虑，为了能够记忆更长历史时间跨度的信息，并能在一定误差范围内运行稳定，本文采用了基于长短型记忆循环神经网络（RNN-LSTM）模型来预测船舶下一位置。并不是每个历史轨迹点位都是重要的，只有在一段时间内有诸多点位数据聚集在某个区域才有意义，这个区域也称为目标位置。为降低系统的复杂度，本文采用了DBSCAN聚类算法来提取历史轨迹中的目标位置序列作为预测模型的输入，并利用Embedding 与LSTM 双层预测模型训练出船舶位置预测模型。

2 船舶位置预测技术概述

2.1 RNN-LSTM模型

循环神经网络在进行训练时，往往为降低模型的复杂度，只会选取若干个隐藏层，而非整个隐藏层作为记忆单元，这样会导致在长时段历史数据上下文语义信息挖掘应用方面存在缺陷，无法做长时序数据挖掘。基于上述原因，Hochreiter 和Schmidhu⁃ber等提出了长短型循环神经网络（RNN-LSTM）［4～5］。RNN-LSTM相较于传统循环神经网络，它从设计上就避免了时序数据预测过程中长短时依赖问题，而设计的关键就是隐藏层中独特的记忆单元结构。如图1 所示，为RNN-LSTM 隐藏层记忆单元结构，该结构包含了三种门，分别是输入门（Input Gate）、遗忘门（Forget Gate）、输出门（Output Gate）。

图1 RNN-LSTM隐藏层记忆单元结构

将RNN-LSTM 隐藏层记忆单元结构比作一个记忆细胞（memory cell），该细胞控制着记忆单元中信息的传播途径。其中A区域表示遗忘区，其中遗忘门（Forget Gate）接收来自上一时刻隐藏层的输出（ht-1）和当前时刻输入（xt）并决定丢弃当前状态下部分信息；B 区域表示更新区，它决定了当前状态需要存储哪些新的信息，并完成记忆细胞的信息更新；C区域表示输出区，其中输出门（Output Gate）决定了当前状态下细胞输出的内容。

根据以上分析，在t时刻，为了计算传给下一个记忆细胞的Ct,ht，现列出记忆单元中输入状态和三个门状态：

Input Gate：

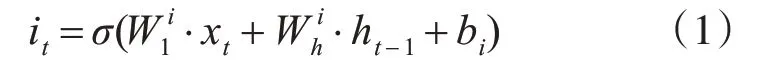
Forget Gate：

Output Gate：

状态输入：

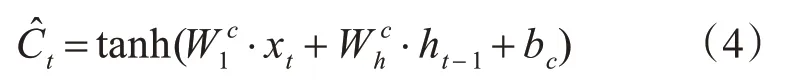
进而求出输出状态Ct和隐藏层输出ht

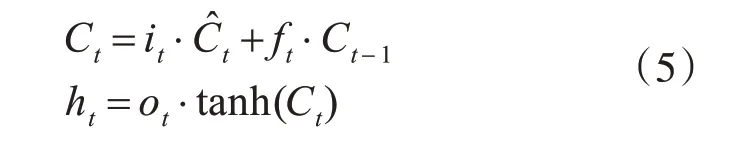
综上，RNN-LSTM 通过门的控制，解决了时序数据预测过程中长短时依赖问题，这对于长时段历史数据预测研究有很好的帮助。

2.2 DBSCAN聚类算法

1996 年Ester M 等［6］提 出 了DBSCAN 聚 类 算法，该算法是一种基于点的周围密度形成集群的聚类方法。在每个聚类的中，可以利用聚类的密度特点，找出任意形态的簇，它们满足簇内的点密度明显高于簇外点的密度这一条件。即DBSCAN 聚类算法可表述为：在一个集合中，定义一个半径为Eps的圆，如果这个圆内落入的点的数目多于所给定最小点数MinPts，则可通过Eps 和MinPts 这两个参数来定义聚类的密度。

关于DBSCAN聚类算法相关的概念定义［7～8］。

定义1给定一个点a，以点a 为圆心，Eps 为半径得到的圆所在的区域叫做Eps邻域。

定义2核心对象（Core objects），如果点a的Eps邻域内样本点数b 大于所给定最小点数Minpts，则称a 为核心对象，b 称为核心点。若样本点落在在Eps邻域的边界上，则称b为边界点。

定义3直接密度可达（Directly density reach⁃able），给定一个样本集合D={d1,d2,…,dn}，如果点di的Eps 邻域内样本点数为b，且d1为核心对象，那么Eps邻域内样本点到di直接密度可达。

定义4密度可达（Density reachable），对于一个样本集合D={d1,d2,…,dn} ，给定数据样本集{p1,p2,…,pn}其中p=p1,q=pn，又假设样本点pi至pi-1直接密度可达，则对象q至对象p密度可达。

定义5密度相连（Density connected），对于一个样本集合D={d1,d2,…,dn}，假设在数据样本集P={p1,p2,…,pn}样本点pi至pj在样本集合P 中的一点d 密度可达，那么样本点pi和pj密度相连。假设样本集合D 中存在一个对象a，使得样本对象p 至q 从对象a 密度可达，则对象q 和p 密度相连。由此可知，密度相连是对称关系，密度可达是直接密度可达的传递闭包。

以上基本介绍了DBSCAN相关定义、聚类原则等。DBSCAN 具有良好的去噪声能力，能够根据点位的疏密程度去除掉其中的噪声区域。此外，DB⁃SCAN 初始值对聚类结果影响不大。基于上述优点，本文选用DBSCAN作为船舶位置停留点聚类提取方法。

3 船舶位置预测分析

3.1 船舶位置预测框架

RNN-LSTM相较于传统循环神经网络，它从设计上就避免了时序数据预测过程中长短时依赖问题，而设计的关键就是隐藏层中独特的记忆单元结构。该结构在增长了记忆范围的同时，能适当的抛弃旧信息。图2 为本文基于RNN-LSTM 神经网络构建的船舶轨迹预测框架。

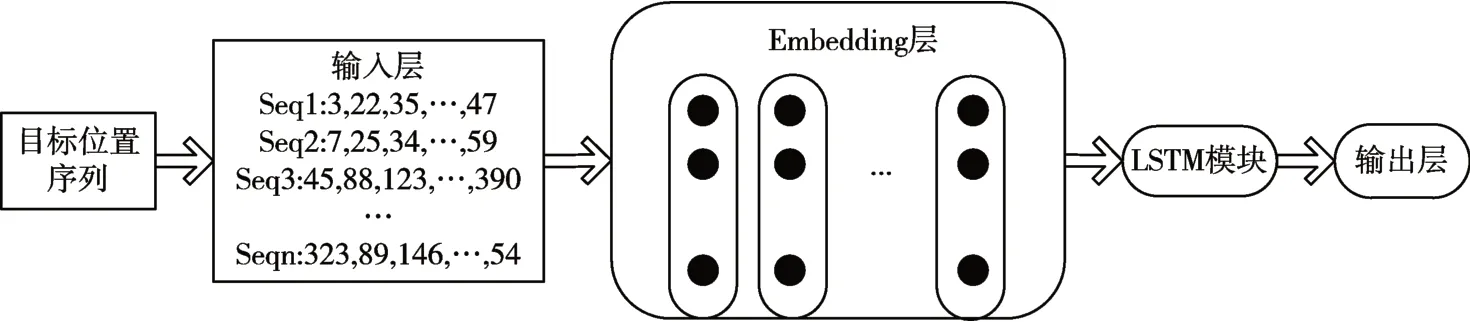
图2 基于RNN-LSTM的船舶轨迹预测框架

由图2可知，基于RNN-LSTM 神经网络构建的船舶轨迹预测框架主要由Embedding层［9］、LSTM模块构成，下面详细介绍这两个模块。

1）Embedding层

正如图2 所示，本文通过DBSCAB 聚类算法提取目标位置，得到了船舶航行目标位置序列。这些目标位置被赋予唯一的标识1,2,3,…,k 。因此可以将目标位置序列转化成索引时序序列，例如1表示港口A，2表示航道B，3表示临时抛锚点C，4表示目的地港口D。假设一条船舶m 从港口A 出发，途径航道B，行驶到C 点进行抛锚作业。但是也可能有另一条船舶n 从港口A 出发，途径航道B，行驶到目的地港口D。由此可知，船舶m 的航行轨迹向量可表示为[1,2,3]，船舶n 的轨迹向量表示为[1,2,4]。通过欧式距离公式计算出的相似度显然非常接近统一轨迹，若已知临时抛锚点C 和目的地港口D方向相反，这样得出的预测结果与实际情况大相径庭。这样可以说明一个事实，那就是如果单纯用索引时序序列来标识目标位置，将不可能得到一个好的预测结果。而本文，为解决上述问题，采用了自然语言中的word2vec模型内的Skip-gram 算法［10～11］，用多维的方式将每一个目标位置对应一个特征向量，这样为区别目标位置提供了更详细的区分度与可能性。

根据Skip-gram算法，相关参数定义如下［12～13］。

由历史轨迹数据提取出来的目标位置集合Q；

目标位置L：其为列向量，长度为k；

目标位置窗口C：以选取目标位置序列中一个元素为中心，上下文宽度为j（向前和向后j 个目标位置）组成的部分轨迹；

条件概率P(C|Li)：表示目标位置Li出现的时候，目标窗口部分轨迹c 出现的概率，其中C(Li)表示所有目标窗口中包含了目标位置Li的集合。

给定模型参数θ，寻求模型参数最大化条件概率乘积如下：

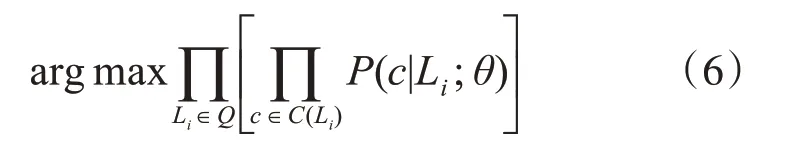
再利用softmax［43］函数对θ 进行处理，将条件概率公式转换成下列公式：

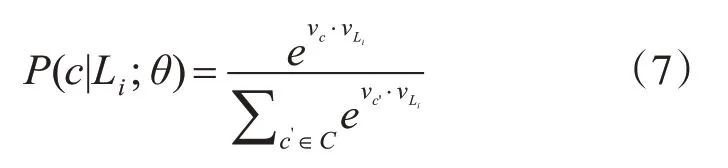
式中，vc、vLi分别表示维度为k的列向量。

通过上述模型表达式可知，模型训练时，其将每一个目标位置用多维特征向量表示，并使得其在目标窗口内条件概率P(C|Li)最大化。由此就可以得出结论，只有特定的目标位置L 才能匹配到特定的目标窗口C。

2）LSTM模块

现结合船舶预测模型，详细介绍LSTM 模块的工作流程如下。

细胞遗忘过程：很多时候，在基于许多已有的历史轨迹属性都已经存入在隐藏层记忆单元结构—记忆细胞内，当预测船舶下一目标位置时，可以立马找到相应的细胞状态。但是当有新的输入时，这就需要去清除较旧的上下文轨迹信息，这就需要通过遗忘门来实现。

细胞状态更新：这一过程是决定当前状态需要存储哪些新的信息，并完成记忆细胞的信息更新。其主要分为两步，一步是输入门输入新的值，它决定需要更新什么值；另一步是Tanh 层建立了一个候选值向量［14］。通过状态更新，使得新增加的目标位置添加到细胞状态中去，以便代替需要被遗忘的信息。

细胞输出：也就是输出门，它决定了当前状态下细胞输出的信息［15］。首先通过Sigmod 层来确定细胞内哪些信息会被输出，然后将这些信息做Tanh 处理，将得到的结果与Sigmod 门的输出相乘，进而最终得到要输出的信息，也就是本文要求得的船舶目标位置概率向量。

结合上文对Embedding 层和LSTM 模块的详细分析可知，本文将离散的目标位置序列作为输入，送入Embedding 层进行计算，从而将目标位置转换成一个固定长度的特征向量。再将Embedding 层全部输出结果送入LSTM 模块内进行遍历，不断调整模型参数，最终使得模型预测下一目标位置成为可能。预测算法实现流程的伪代码如下。

算法名：基于RNN-LSTM的船舶位置预测算法

Input：A set of trajectory

Process：

1：X=generateSeqSample（trajectory）；

2：Y=generateNextPlace（trajectory）；

3：model=sequential（）；

4：model.add（Embedding（））；

5：model.add（LSTM（））；

6：model.add（Dropout）；

7：model.add（Dense）；

8：model.add（Activation）；

9：model.compile（loss=，optimizer=）；

10：model.fit（X，Y）；

11：model.evelate（）；

Output：an index of future target location

前期通过DBSCAB 聚类算法提取目标位置，得到了船舶航行目标位置序列。为了训练预测模型，第1、2 行代码分别表示了目标位置序列样本输入和目标位置对应的下一位置。由于本文所提预测模型是一个线性模型，所以创建了一个Sequential模型（第3 行）。接下来是创建Embedding 层和LSTM 模块，以用来构建目标位置特征向量和模型训练（第4、5 行）。与此同时，要选好模型使用的激活函数以及做好措施防止过拟合问题（第6、7、8行）。最后是模型预测效果验证，将训练好的模型代入待测试的数据，来预测下一步船舶可能出现的位置（第9、10 行）。需要强调的是，此模型的输出并非是一个确定的地点，而是一个概率分布，所以需要根据概率借助索引找到最有可能的目标位置（第11行）。

3.2 船舶下一位置预测

前一小节详细介绍了船舶位置预测框架流程，但未将LSTM 模块中如何预测加以详述。本节将详细推导从部分历史目标位置序列来预测船舶下一位置这一过程。如图3 所示，为简化后的循环神经网络预测结构模型，只展示出了隐藏层结构。

图3 循环神经网络预测结构模型

目标位置序列经由Embedding 层计算之后，使得目标位置转换成相应的多维特征向量X=[x1,x2,…,xT]，接着将这些多维特征向量送入拥有N 层隐藏层线性结构的RNN 中去，通过迭代计算得到n层隐藏层线性输出为，最终经由输出层得到目标序列Y=[y1,y2,…,yT]。目标序列中，每一个元素yi都是一个M维向量，其中每一维对应下一目标位置的概率。而本文则是利用得到的目标序列中每一个结果向量yt与下一个目标位置特征向量xt+1得出预测分布Pr(xt+1|yt)。

由于本文所设计的模型框架只有一层LSTM隐藏层，所以从t=1 至t=T 时刻（一般目标位置序列中第一个元素为空值），隐藏层内激活函数迭代计算公式如下：

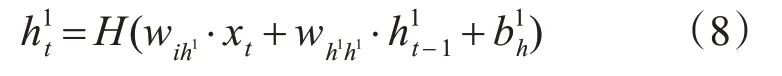
式中，H 为激活函数，w 为输入层与隐藏层之间的权值，b 为偏移值。

在得到隐藏层输出后，需要在输出层计算船舶位置预测概率，公式如下：

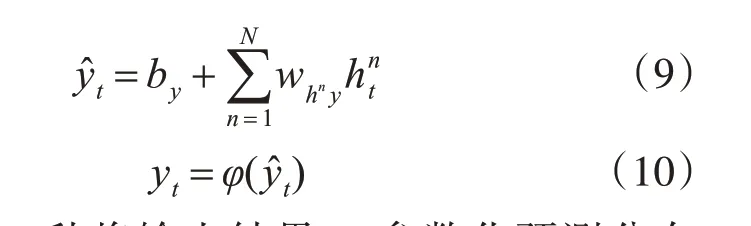
式中，φ(⋅)是一种将输出结果yt参数化预测分布Pr(xt+1|yt)的输出函数。通常在实际数据中难以寻找到一个合适的预测概率分布，而本文可得到一个目标位置序列Traj 的概率公式如下：

训练模型的损失函数如下：

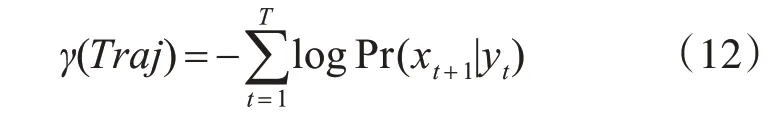
4 实验结果与分析

4.1 实验数据集

研究过程中实验数据是由自主设计的GPS 采集设备获得。实验采集设备一共有5 个GPS 信标，选取了其中3 个测量精度较好的信标。实验数据统计见表1所示。

表1 实验数据集

为保证实验的真实性，本实验场地选在无锡市长广溪国家湿地公园，实验数据源一共包含了3 个实验GPS 节点（模拟3 条船只），共计150 条轨迹轨迹信息，且平均每条轨迹包含了180 个GPS 轨迹点。由于GPS 采集设备精度以及冷启动等因素的存在，该系统所采集到的位置数据中可能存在异常值。为避免这些异常值对后续各算法流程的影响，在软件设计时，就采用了偏移处理算法滤除了这些异常值。同时为抑制采集系统中的高斯噪声，所有采集到的轨迹数据均利用扩展卡尔曼滤波算法的船舶位置数据预处理模型来做船舶GPS 数据预处理。

4.2 评价指标

本小节所介绍的评价指标是用于权衡基于循环神经网络的船舶轨迹预测的实验结果。主要评价指标包括准确率（precision）、召回率（recall rate）和F值（F-measure）。

假设实验中预测结果集为Q，其中准确的结果集为T，则相应的实验评价指标公式如下：

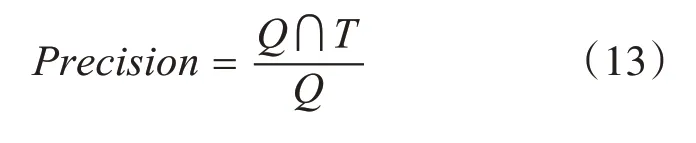
式（13）是准确率，表示预测结果集Q 中正确结果所占比例。

式（14）是召回率，表示准确的结果集T 中正确结果所占比例。

式（15）是综合评价指标，指准确率和召回率的调和平均值。

4.3 船舶位置提取与预测结果

DBSCAN 聚类算法调节过程中包含了Eps 和MinPts 两个主要参数。其中Eps 指邻域半径（聚类时每一个点），MinPts指以Eps为半径的邻域内拥有轨迹点的最少个数。聚类分析过程中MinPts 设定为3，若MinPts ≥3 时，则被视为一个簇。表2 是调节Eps和MinPts两参数后DBSCAN聚类效果统计。

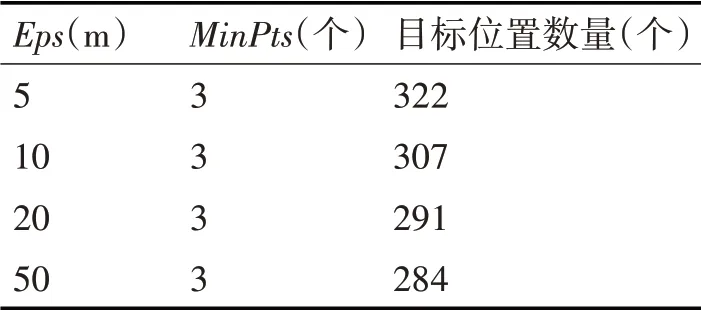
表2 DBSCAN参数调节效果

由表2 可以看出，当MinPts 一定时，提取到的目标位置数量随着Eps 的增大而减小。根据表中数据结合实验经验，现将Eps=20,MinPts=3 作为聚类条件。由此，聚类分析之后，150 条轨迹数据提取出了291个目标位置，同时将整理成50条时序目标位置序列。

通过聚类分析提取的目标位置序列，将作为循环神经网络训练模型的数据集，用来进行预测模型的训练。实验将取出20%的数据集作为测试数据，其余将用于预测模型训练。

在使用LSTM 进行位置预测时，会有多种因素影响着系统的预测效果。下面将分不同参数条件来讨论模型预测的准确率。

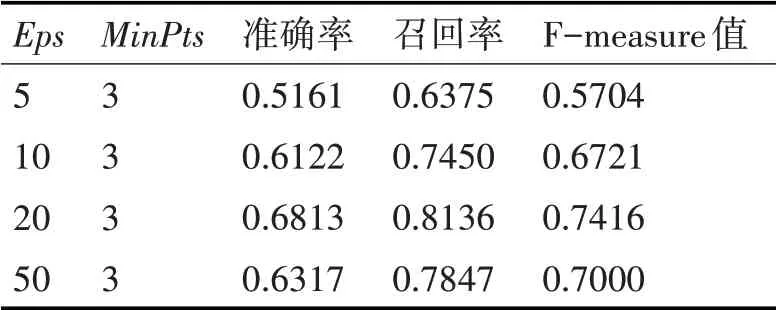
表3 DBSCAN聚类参数Eps对预测模型的影响

表3 展示了DBSCAN 聚类算法在取不同邻域半径Eps 时对LSTM 模型预测结果的影响。当MinPts为固定值时，随着Eps的增大，邻域半径内满足MinPts条件的轨迹点会越来越多，更多的停留点被聚合在了一起，这样相似的轨迹数量会越来越多，但也会出现聚类算法能够提取到的目标位置变少的状况。进一步分析可知，当Eps 的增大时，正是由于相似的轨迹数量越来越多，增强了模型的记忆训练，从而使得预测准确率从51.61%升至68.13%。但Eps 也不是取越大越好，若是越大，会导致能够提取到的目标位置越来越少，使得送入模型的目标位置序列长度无法反映真实的运行轨迹，不利于模型预测。

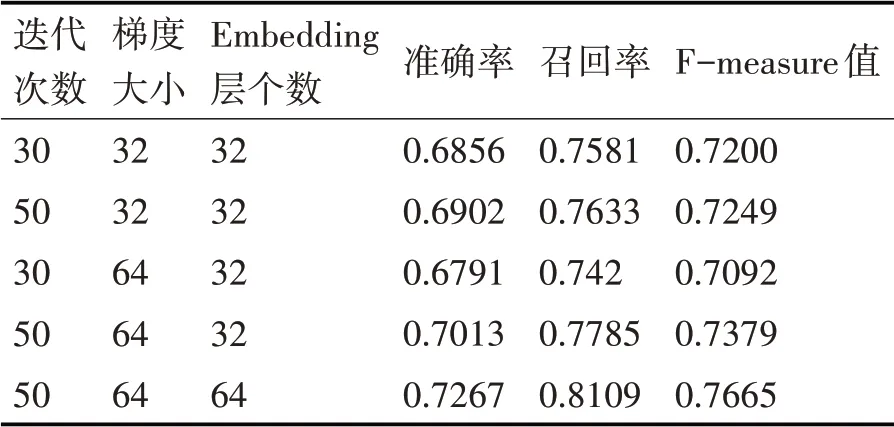
表4 LSTM模型参数对预测结果的影响

表4 展示了在进行循环神经网络数据训练时，模型参数调节对预测结果的影响。由上表可知，其他参数一定时，随着模型的迭代次数、梯度更新块大小、Embedding 层个数的增加，系统的预测准确率也会提升；其中梯度更新块增多，会提升模型的训练速度，也会使预测结果趋于平稳。经过试验调整，可以看到当迭代次数设定为50、梯度更新块设定为64、Embedding 层数设定为64 时，本文提出的基于RNN-LSTM 的位置预测模型拥有较好的预测结果，预测准确率为72.67%。

4.4 实验结果对比

上一小节已经验证了基于RNN-LSTM 的船舶位置预测模型的可用性。为了进一步验证模型的准确性与研究的必要性，本文将选取传统历史轨迹位置预测模型如概率模型或马尔科夫模型进行对比分析。

为保证本文提出的预测模型处于最佳状态，因此设定LSTM 模型各参数依次为：迭代次数设定为50、梯度更新块设定为64、Embedding 层数设定为64。此外，DBSCAN 聚类分析时，设定邻域半径Eps设定为20、邻域半径内最少轨迹点数MinPts 设定为3。

如图4、图5、图6 分别是各模型准确率、召回率、F-measure 值对比分析图。其中1-MM 是一阶马尔科夫模型、2-MM 是二阶马尔科夫模型、1-VOMM 是一阶变阶马尔科夫模型、2-VOMM 是二阶变阶马尔科夫模型。由对比图可以看出，在准确度上，LSTM 模型达到72.67%，高出二阶变阶马尔科夫模型13.3%；在召回率上，LSTM 模型达到81.3%，高出一阶变阶马尔科夫模型9.4%；在F-measure 值上LSTM 模型达到76.47%，高出二阶变阶马尔科夫模型12.24%。

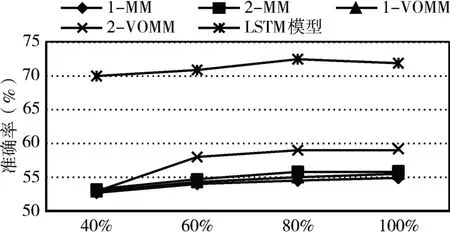
图4 各模型准确率对比

图5 各模型召回率对比

图6 各模型F-measure值对比

综上，基于循环神经网络的船舶位置预测模型相较于传统基于马尔科夫预测模型具有较高的预测精度，具有一定的研究价值。

5 结语

为解决在长时序跨度条件下，针对传统马尔科夫模型预测船舶的下一位置精度较低且系统复杂度较高的问题，本文提出了基于长短型记忆循环神经网络的船舶位置预测模型。该模型依据船舶轨迹数据庞杂而有序的特点，为降低系统复杂度，采用了新颖的DBSCAN 聚类算法来提取船舶轨迹数据中的目标位置序列，同时为了获得更好的目标位置区分度，引入了Embedding 层，利用自然语言中的word2vec 模型内的Skip-gram 算法，将每一个目标位置用多维特征向量表示，最终将已构建好的目标位置特征向量送入LSTM 模块中进行模型训练，进而利用模型预测出下一目标位置。实验结果表明，所提模型相较于传统模型具有较高的预测准确性。在后续的研究中，要综合考虑不同影响因素对所建船舶位置预测模型造成的影响，并结合实际应用场景，让船舶位置预测模型较好地进行商业化探索。