具有介质访问约束的网络化控制系统控制策略
祝超群,党泽坤
(兰州理工大学a.电气工程与信息工程学院;b.甘肃省工业过程先进控制重点实验室;c.电气与控制工程国家级实验教学示范中心,甘肃兰州730050)
网络化控制系统(networked control system,NCS)借助实时通信网络来实现控制器与传感器/执行器之间的数据交换。与点对点传输信号的传统控制系统相比,NCS具有诸多优点和很强的实用性,其不仅使信息传输更方便快速、连线更简单,还可实现网络资源的共享利用,使对被控对象的远程控制变为现实。因此,NCS普遍应用于自动化制造、航空航天及电气制造业等领域。数据在网络中进行传输,不可避免地会引起各种通信问题,如网络诱导时延、介质访问约束、量化误差、由于网络阻塞产生的丢包现象及通信受限问题等。其中,介质访问约束对系统控制性能影响较大,会造成系统性能下降甚至失稳。介质访问约束是指由于通信带宽的限制,在每个采样周期内仅有部分传感器/执行器能够获得网络信道与控制器进行通信。介质访问约束主要存在于具有数量众多的传感器/执行器和有限通信网络的大系统中,如海面溢油监测系统、复杂工业过程控制系统等。
学者们针对具有介质访问约束的NCS进行了广泛研究。Brockett针对系统中存在的介质访问约束现象,首次提出采用通信序列对网络节点的访问顺序进行描述,在此基础上研究了系统稳定控制律的存在性问题;Sreram等针对具有介质访问约束的NCS,提出一种随机最优控制方法,通过仿真实例说明采用控制方法的有效性;Tian等研究了具有通信约束的NCS鲁棒控制问题,考虑传感器和控制器以及控制器与执行器通道的介质访问约束,利用Lyapunov 泛函和线性矩阵不等式(linear matrix inequality,LMI)技术设计均方稳定控制器;祝超群等考虑控制器与执行器之间由于网络带宽产生的介质访问约束,通过Lyapunov稳定性理论得出系统稳定的充分条件,使网络化系统随机稳定。控制和测量信号在数字通信网络中传输必然要进行信号量化,而信息量化精度对控制系统的性能提出了巨大挑战。目前,NCS中的量化问题受到众多学者的高度重视,Kalman考虑采样控制系统中信号量化问题,指出若闭环系统的控制使用一种有限水平量器时,系统将会出现混沌行为;Ren等研究了离散时系统在数据量化和通信约束下的线性最小均方估计问题,利用正交投影原理,设计一个卡尔曼滤波器,通过算例验证了该方法的有效性;陈刚等借助逆凸技术和自由权矩阵方法,研究一类带有信号量化的NCS渐近稳定性问题;Peng等研究非线性NCS的动态量化镇定控制问题,通过建立网络化系统的模糊模型,利用Lyapunov-Krasovski方法保证了系统的渐近稳定;Cheng等研究一类具有量化和带宽约束的网络化系统的最优跟踪控制问题。
由上述文献综述可知:多数学者将介质访问约束和信号量化问题独立进行研究,这与网络控制实践具有一定差距;多数网络化系统控制综合采用基于状态的控制方案,实际系统控制中,系统状态很难通过直接测量获得。基于上述问题,针对同时存在访问约束和信号量化的网络化系统,提出一种动态输出反馈控制策略,该控制策略只需系统的输出信息,便可实现系统的全局反馈。
1 系统描述
NCS的结构如图1,被控对象的离散线性时不变状态方程可描述为:

其中:x( k )∈R,u( k )∈R,y( k )∈R,分别表示系统的状态、输入和输出;A,B,C 为适当维数的常数矩阵。
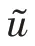
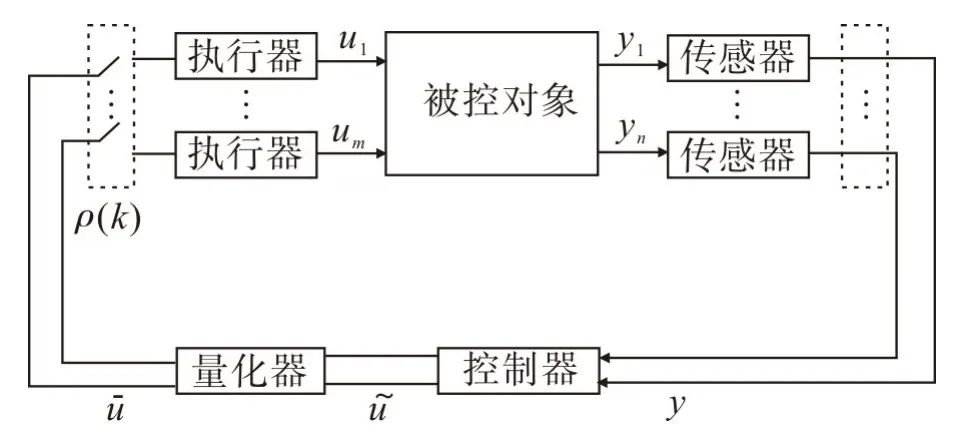
图1 网络化控制系统结构Fig.1 Structure of networked control systems
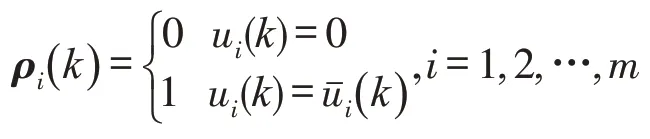
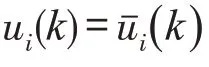

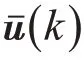
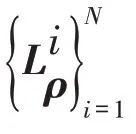
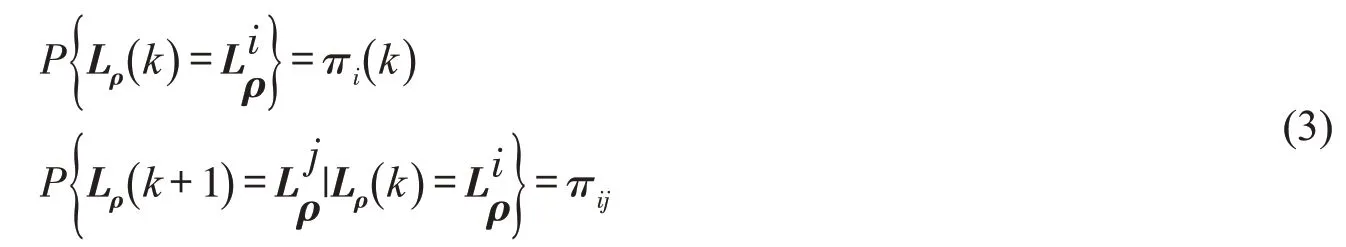
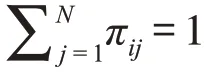
针对数据传输过程中的量化问题,在控制器与执行器之间引入对数量化器f(·)。假设不同模态的量化器相同,因此可记f(·) =f(·) ,将量化器f(·) 定义为
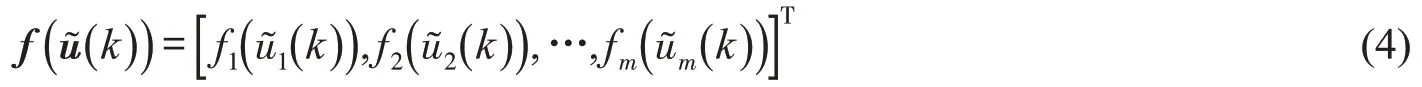
定义
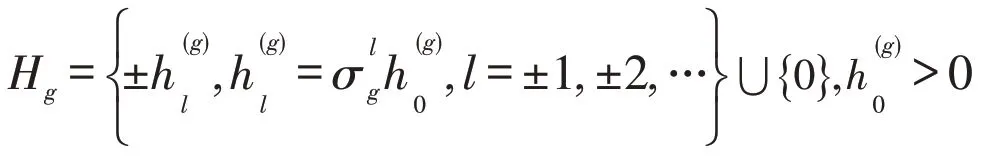
其中:H表示相应的量化级集合;σ为量化密度且是一个给定值。
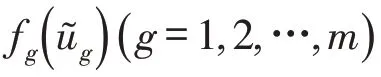
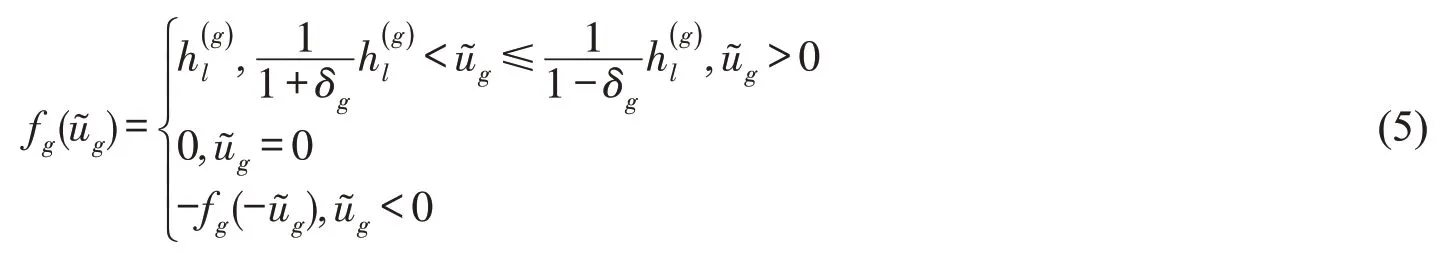
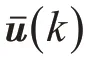

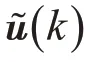
因此,在同时具有访问约束和信号量化的条件下,可得闭环控制系统方程为:
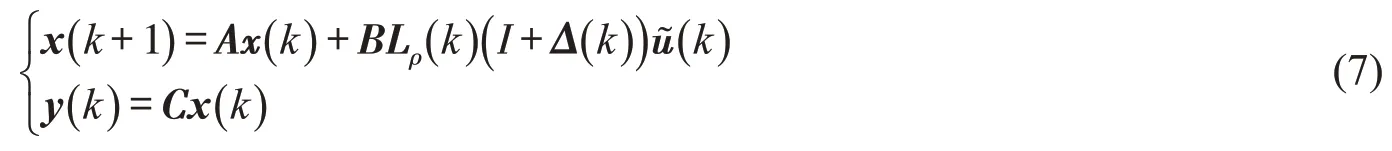
2 动态输出反馈控制器设计
针对具有访问约束和信号量化的网络化系统,设计动态输出反馈控制器,如

其中:x( k )∈R( φ ≤n )为控制器的状态;A,B,C为适当维数的常数矩阵。若φ=n,对系统状态进行满阶动态补偿;若φ <n,则对系统状态进行降阶动态补偿。
联立式(7)和式(8),令增广向量为

则增广的闭环网络化控制系统为

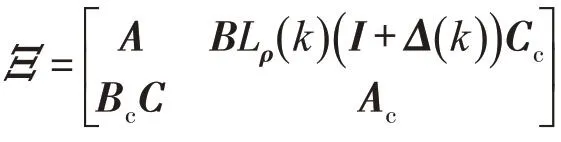
为对闭环系统(10)进行稳定性分析和控制器设计,给出以下引理:
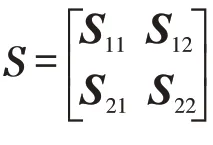
1)S <0;
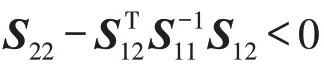
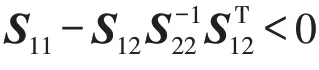
引理2
已知M,N 为适维矩阵,F 满足FF ≤I,W=W,那么W+NFM+MFN <0
当且仅当存在标量ε >0,使得
W+εNN+εMM<0
为便于描述,将Δ( k )简记为Δ,矩阵中的∗表示对角矩阵中对应矩阵的转置。
定理1
对于具有访问约束和信号量化的NCS,若存在正定矩阵Q,H,矩阵W,V,U,标量ε>0,ε>0,使得下列矩阵不等式成立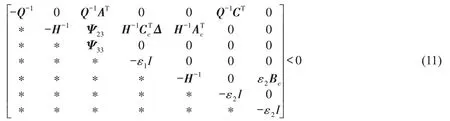
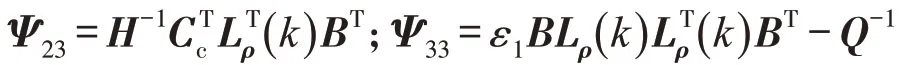
证明
选取Lyapunov函数为V( k )=x( k )Qx( k )+x( k )Hx( k)
其中Q,H 为对称正定矩阵。
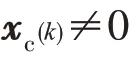
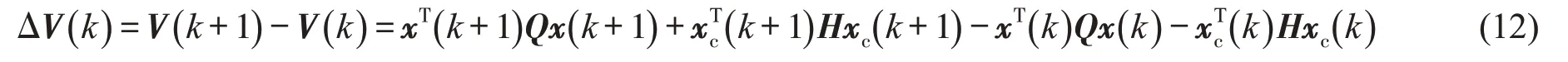
将式(7),(8)代入式(12),可得

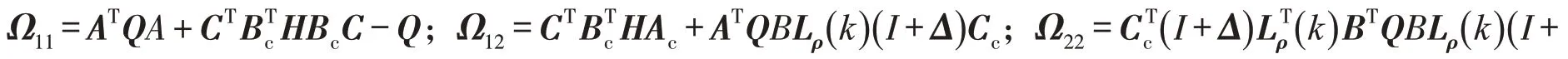
根据Lyapunov函数稳定性理论可知,闭环系统(10)渐近稳定的充分条件是

令
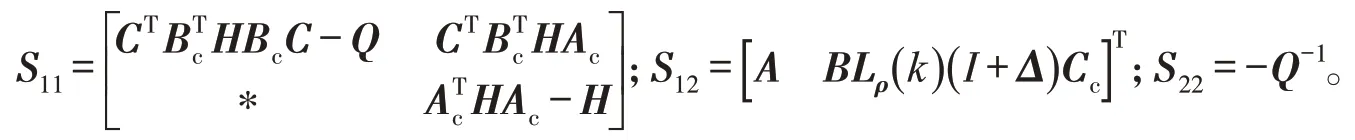
对式(14)应用引理1,得
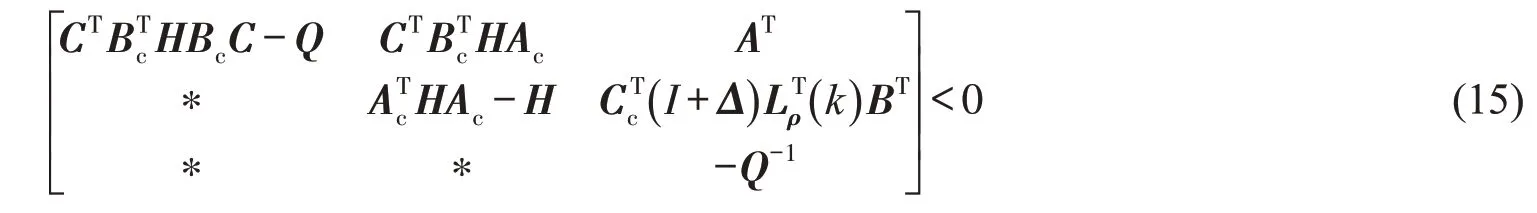
则式(15)可以表示为

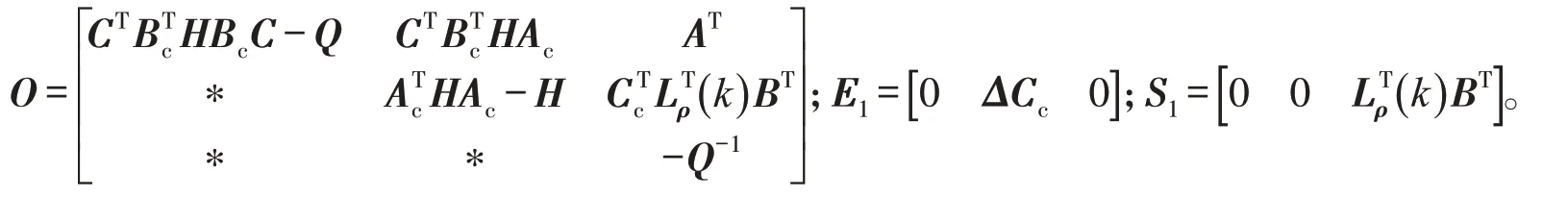
对式(16)应用引理2,可得
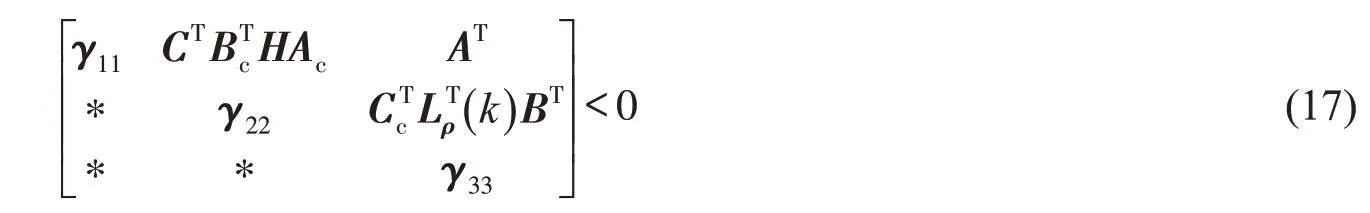
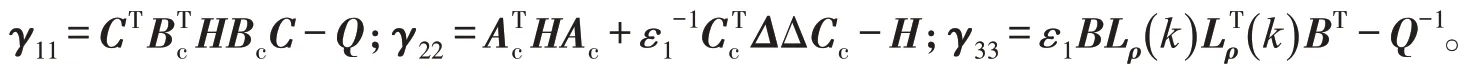
令
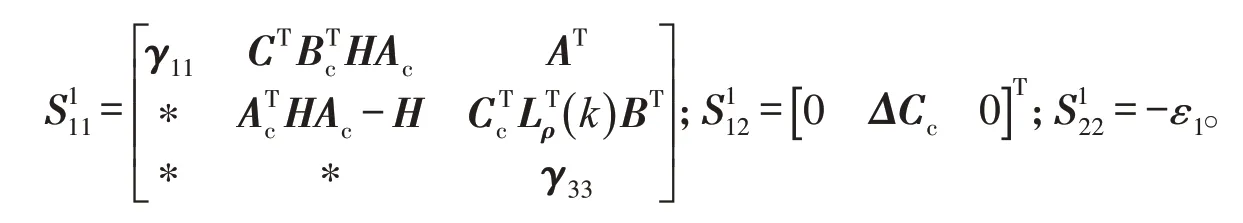
对式(17)应用引理1,可得
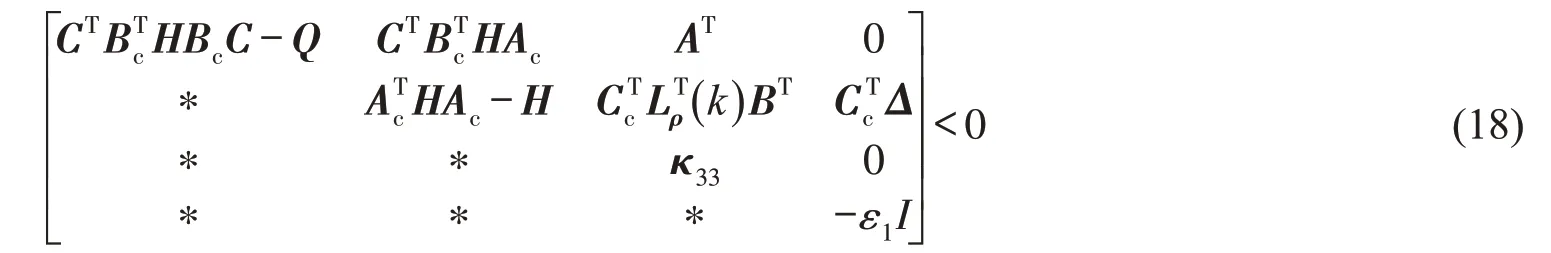
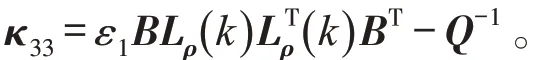
令
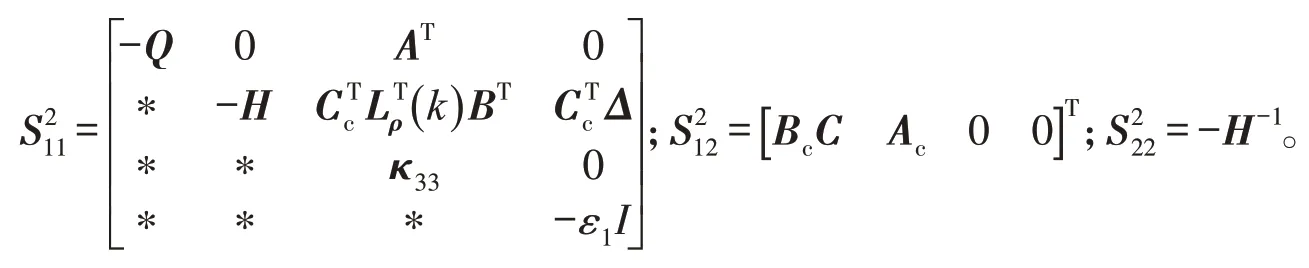
对式(18)再次应用引理1,可得
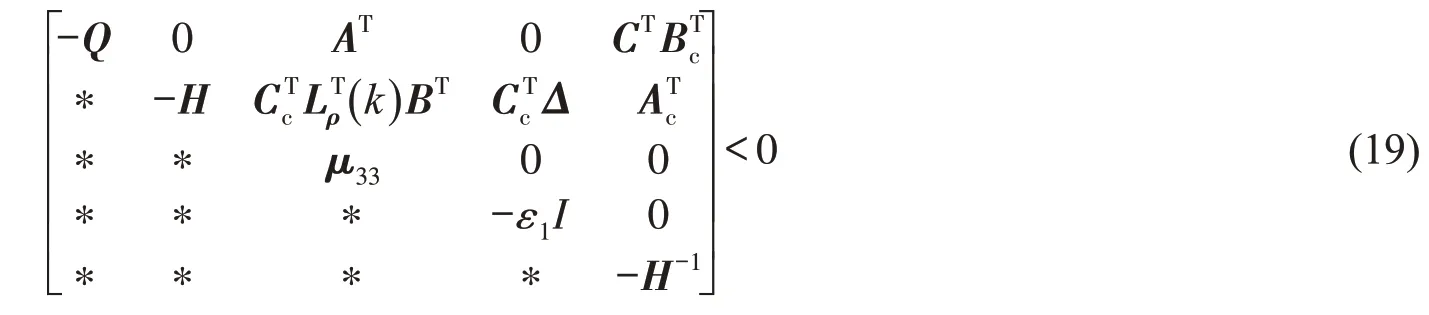
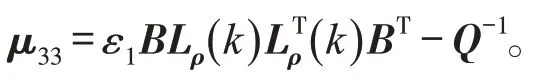
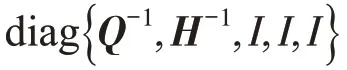
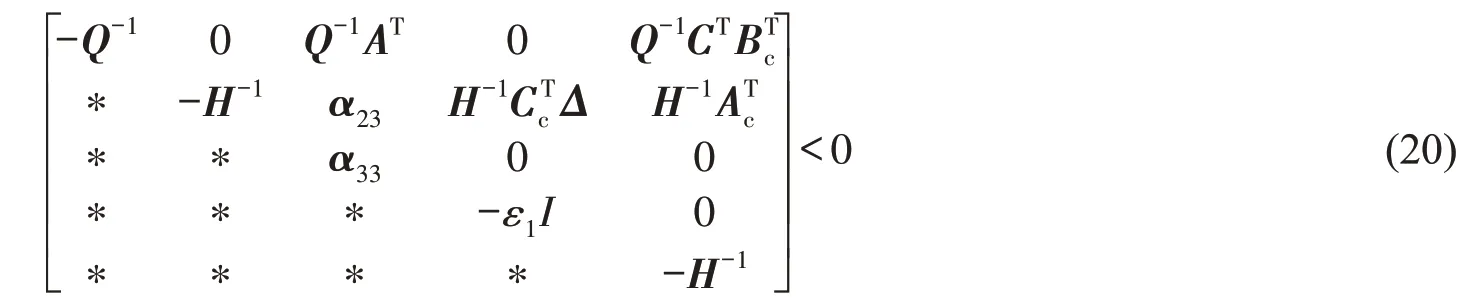
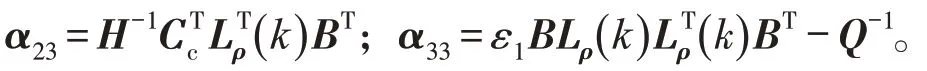
则式(20)可写成

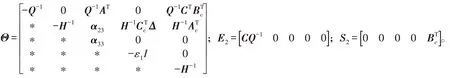
对式(21)应用引理2,则有
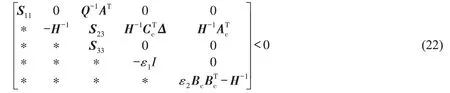
令
对式(22)应用引理1,可得
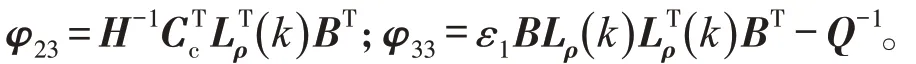
令
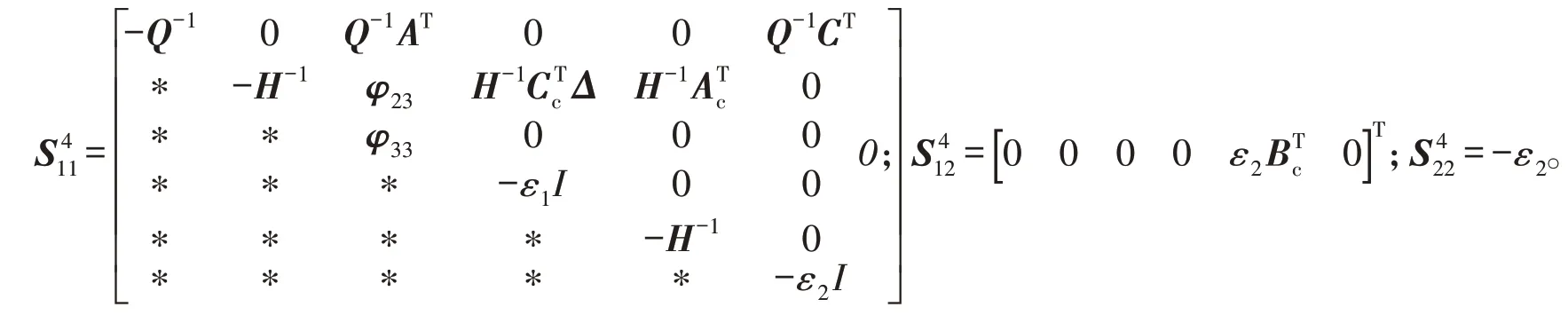
对式(23)再次应用引理1,可得

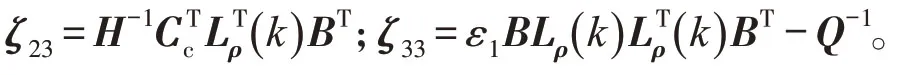
定理2
对于具有访问约束和信号量化的NCS,若存在正定矩阵Q,H,矩阵W,V,U,标量ε>0,ε>0,使得下列矩阵不等式成立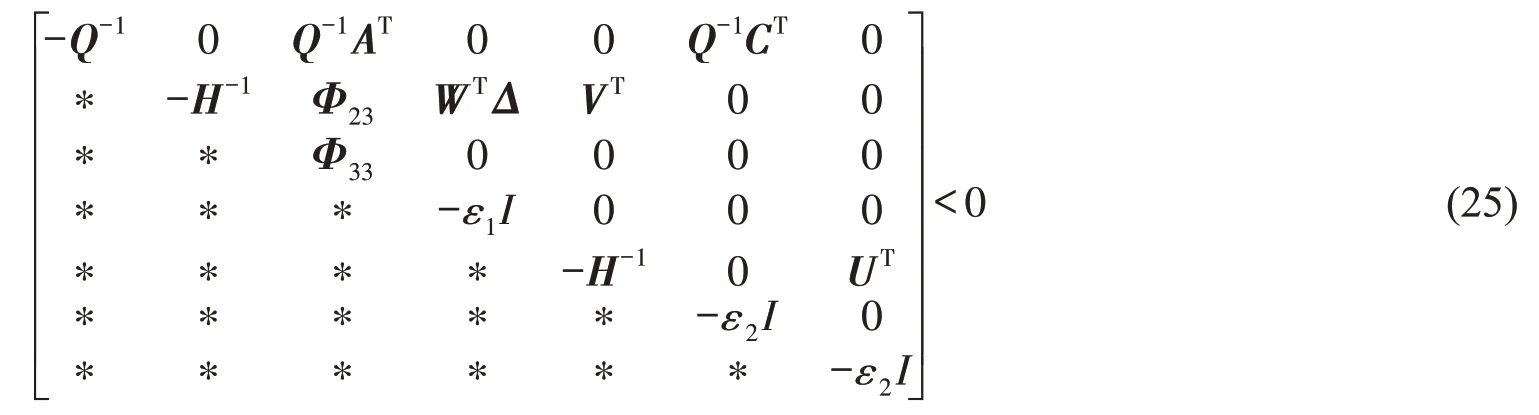
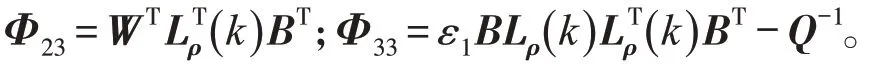
当矩阵不等式(11)有可行解时,动态输出反馈控制器为:

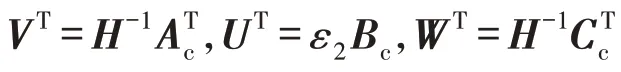
3 仿真算例
考虑如下开环不稳定的线性离散时间被控对象:

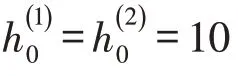
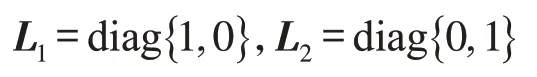
根据定理2,利用LMI工具箱求解式(26)可得如下动态输出反馈控制矩阵

选择系统初始状态x=[4 -1],根据设计的动态输出反馈控制器(式(26))进行仿真,得到仿真曲线,结果如图2~5,其中横坐标k 表示系统的采样周期。图2纵坐标中的“1”和“2”表示对应的随机通信矩阵,分别为L和L。由图3可看出,在前期系统输出波动较大的情况下,在有限个采样周期内系统输出快速趋于稳定状态。由图4可看出,初始阶段量化误差e 的波动较大,当进入到第20个采样周期时,系统的量化误差趋于零值。由图5可看出,在给定的初始条件下,文中设计的动态输出反馈控制器可使闭环系统(式(10))的状态快速收敛于平衡状态,且具有良好的动态性能。
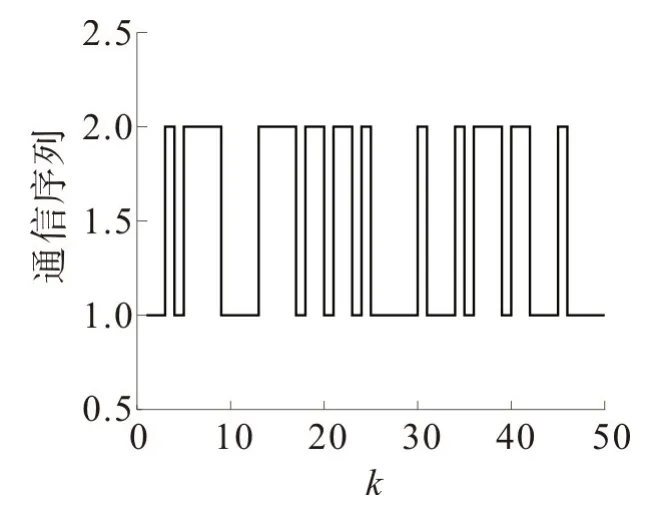
图2 介质访问序列的模态切换曲线Fig.2 Curves switch mode of medium access sequence
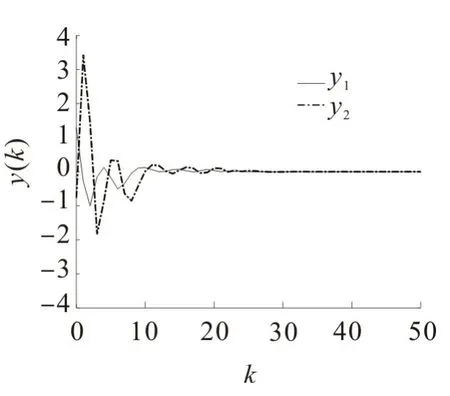
图3 系统输出信号Fig.3 System output signal
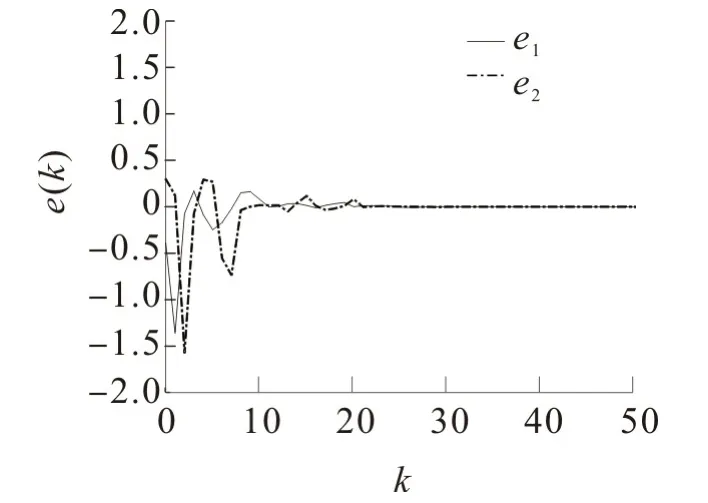
图4 控制输出量化误差Fig.4 Quantization error of control output
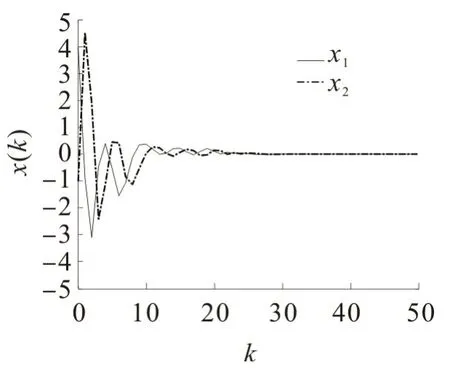
图5 状态轨迹Fig.5 State evolution
为进一步说明文中控制策略的优越性,在同样初始条件下,采用文献[18]中的控制策略,系统状态轨迹和量化误差分别如图6,7。对比图4,7及图5,6可看出,文中控制策略下,系统的状态和量化误差波动较小,系统状态收敛于平衡状态的速度较快,且具更好的控制性能。
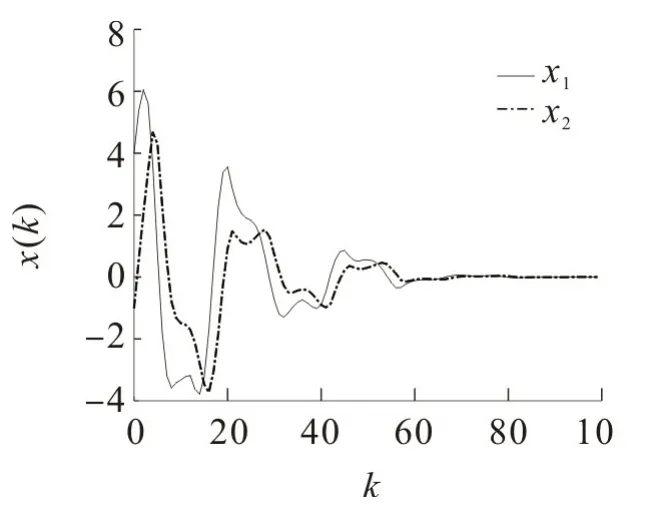
图6 文献[8]中控制策略状态轨迹Fig.6 State evolution of control strategy in reference[8]
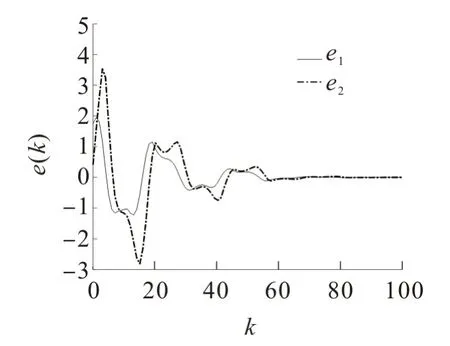
图7 文献[8]中控制策略控制输出量化误差Fig.7 Quantization error of control output of control strategy in reference[8]
4 结 论
针对同时存在介质访问约束和信号量化的NCS,研究系统的动态输出反馈控制问题,提出一种具有介质访问约束的网络化控制系统控制策略。由于有限网络带宽的限制,在每个控制周期只有部分控制信号可传输到执行器执行控制任务。根据执行器的信道随机访问机制,采用对数量化器对控制信号进行量化,将NCS建模为等价的Markov跳变系统;借助Lyapunov稳定性理论和LMI技术推导出系统稳定的充分条件,在此基础上设计动态输出反馈控制器,实现NCS的镇定控制。仿真结果表明本文提出的动态输出反馈控制策略是有效的,可使系统状态迅速收敛于平衡状态。

