跟踪微分器在磁浮列车悬浮间隙处理中的应用*

张文跃 佟来生 王 滢 侯 磊 朱跃欧

(1. 中车株洲电力机车有限公司， 412001， 株洲；2. 西南交通大学电气工程学院， 611756， 成都∥第一作者， 高级工程师)

悬浮系统是磁浮列车的核心子系统，而悬浮间隙检测的准确度对于实现整个悬浮系统的平稳控制具有重大影响。一般采用非接触式的电涡流传感器进行悬浮间隙检测，但磁浮列车通过轨道接缝时，由于接缝处没有金属材料，无法形成感应涡流，因此悬浮间隙检测值会发生信号失真(见图1)，严重影响磁浮列车的悬浮性能。

图1 悬浮传感器路间隙探头过轨道接缝时的输出特性

为了解决上述问题，现有的方法是：在磁浮列车运行方向设置多个悬浮间隙探头(见图2)，通过多路信号比较，舍弃畸变信号而保留其他正常信号，以提高检测准确度。但该方法对于磁浮列车高速行驶时或通过连续密集轨道接缝时，可能会出现两路甚至三路悬浮间隙检测值同时畸变的情况，导致悬浮系统控制效果恶化甚至失稳。为此，本文提出了一种基于双曲正切的非线性跟踪微分器(TANH-TD)结合联合滤波的悬浮间隙处理方法，能够获取更准确的悬浮间隙信号，可进一步提高悬浮系统的稳定性和可靠性。

1 TANH-TD原理

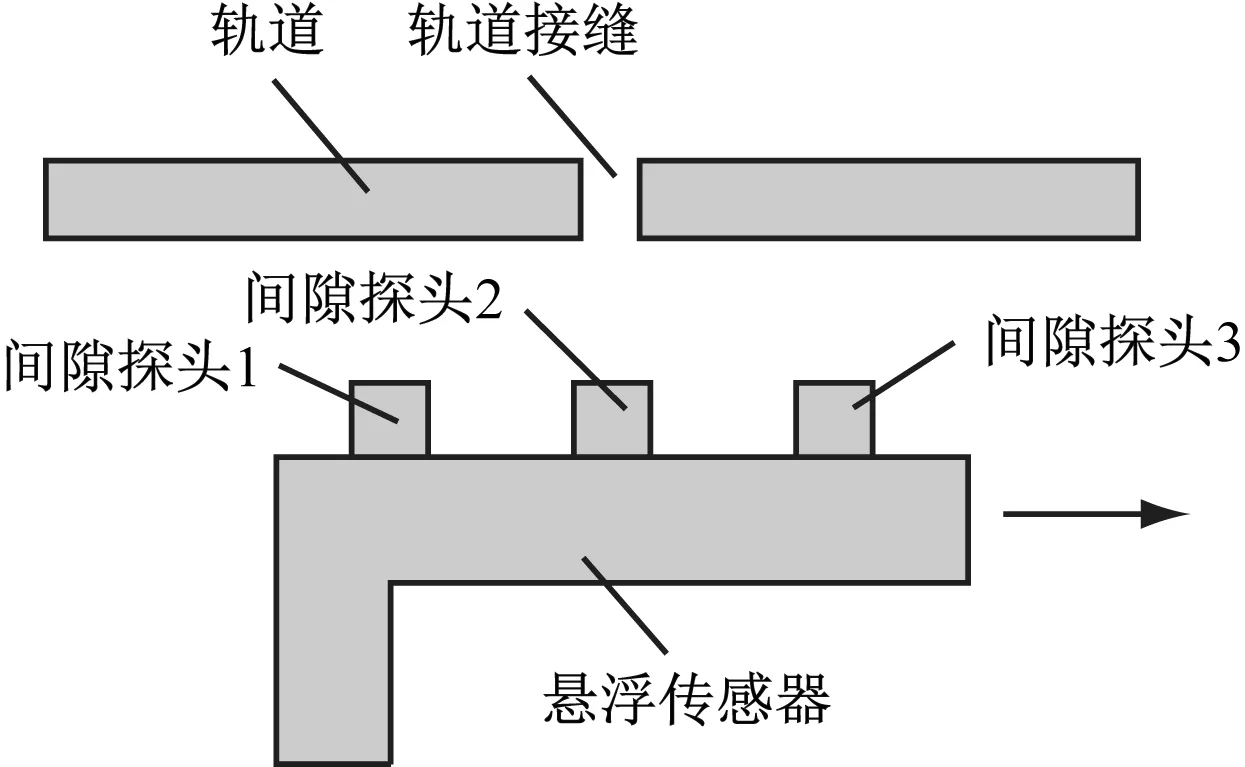
图2 悬浮传感器探头分布及通过轨道接缝示意图

若系统

(1)

的任意解均满足：z1(t)→0,z2(t)→0,其中t→∞，则对任意有界可积函数v(t)和任意常数T>0，系统

(2)

的解x1(t)满足

(3)

式中：

R——系统时间尺度参数；

x1,x2——分别为系统跟踪信号和近似微分；

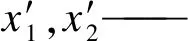
上述定理表明了x1(t)是的对原函数v(t)的平均收敛，x2(t)弱收敛意义下对函数v(t)导数的近似微分。

为了便于工程实际应用，根据二阶离散系统最速综合控制函数给出上述定理的离散形式[2]：

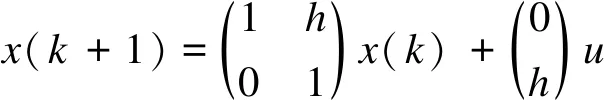
(4)

式中：

h——采样步长；

x(k)=(x1(k),x2(k))T——t=kh时的系统输出信号；

u——综合控制函数。

综合控制函数主要影响跟综信号x1(t)和微分信号x2(t)跟踪收敛的动态性能，其选取的首要原则是在接近平衡点时应具有线性函数特点，而在远离平衡点时应具有非线性函数特点，以保证跟踪的快速性并减小因控制器切换产生的抖振；其次，函数特性应该尽量光滑、连续，参数整定应尽可能简单易行。

针对跟踪微分器综合控制函数形式复杂、参数较多、整定繁琐及输出抖振等问题，采用双曲正切函数作为综合控制函数来设计跟踪微分器。下面给出综合控制函数的具体形式[3]：

(5)

式中：第一项表示t时刻跟踪误差[x1(t)-v(t)]对综合控制函数的影响，a1、b1为跟踪误差[x1(t)-v(t)]的权重系数；第二项表示t时刻近似微分x2(t)对综合控制函数的影响，a2、b2为近似微分x2(t)的权重系数。为了均衡考虑t时刻跟踪误差[x1(t)-v(t)]和近似微分x2(t)对综合控制函数的影响，不妨令a2=a1=a,b1=b2=b。

双曲正切函数在原点附近有良好的近似线性性质，而在远离原点时具有非线性函数的特点，满足跟踪微分器综合控制函数的要求，同时由于函数光滑连续，有利于较小甚至消除系统的输出抖动。

2 TANH-TD的数值仿真

为分析TANH-TD的滤波性能和跟踪效果，构建跟踪微分器的仿真模型，并进行数值仿真。设置采样频率为1 000 Hz，输出跟踪信号和微分信号的初试状态为零，然后仿真分析TANH-TD对带噪声的正弦信号滤波性能和对阶跃信号的跟踪性能。为分析时间尺度参数R对跟踪微分器输出的影响，采用带有方差为0.3的高斯白噪声的正弦信号作为输入，参数a和b的取值分别为18.0和0.1，R取值分别为10.0、50.0、100.0，仿真结果如图3所示。为探究参数a对跟踪微分器输出的影响，以a取值分别为1.0、10.0和20.0，R和b取值分别为20.0和0.1进行数值仿真，仿真结果如图4所示。为研究参数b对跟踪微分器输出的影响，以b取值分别为0.1、1.0和10.0，R和a取值分别为20.0和18.0进行数值仿真，仿真结果如图5所示。

1) 由图3可见：R取值越大，输出跟踪信号滤波效果越差，但是跟踪性能优越；R取值越小，输出跟踪信号滤波效果越好，但是存在较大的时延，跟踪效果不佳。

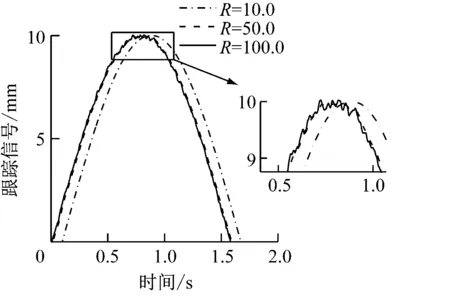
图3 参数R对跟踪器输出的影响

图4 参数a对跟踪器输出的影响

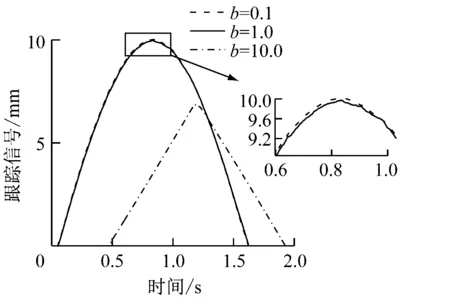
图5 参数b对跟踪器输出的影响

2) 由图4可见：a取值越小，输出的跟踪信号滤波效果越好，但存在较大偏差，跟踪效果不佳；a取值越大，输出跟踪信号滤波效果变差，但是跟踪性能较好。但同时也发现，当a=10.0和a=20.0时，跟踪性能差距不明显，说明在a增大到一定程度后，继续增加对跟踪性能影响基本不大。

3) 由图5可见：b取值越大，输出跟踪信号滤波效果越差，且跟踪性能也变差，当b=10.0时，跟踪信号不仅相位滞后而且误差明显；b取值越小，输出跟踪信号滤波效果和跟踪效果均有提升。但同时也发现，当b=1.0和b=0.1时，跟踪性能差距不明显，但滤波性能仍有提升，说明在b增大到一定程度后，继续增加只对滤波性能有影响。

综上可知，R作为系统时间尺度参数，其选取应权衡滤波性能和跟踪性能的需求；a作为综合控制函数的幅值，其在一个既定范围内是与跟踪性能成正比的，故选取时应该注意不宜过大；b作为综合控制函数的近似线性区间的斜率，其取值应尽量小，过大会造成跟踪信号的幅值和相位严重失真。

3 基于TANH-TD的三路间隙联合滤波

悬浮传感器在采集间隙数据时会受到电磁场、轨道误差等各种因素干扰，信号中往往带有噪声，其微分信号的提取也很困难，不利于判断其信号值突变是否由过轨道接缝引起。目前，磁浮列车对悬浮间隙信号的处理主要是：通过空间错开一定距离的3个间隙探头所测得的数据(S1、S2、S3)先滤波，然后再根据过轨道接缝时刻不同来分离出一个比较可靠的间隙值。这种每时每刻舍弃三路悬浮间隙数值中最大的一个数据，并取另外两路悬浮间隙均值的方法，可在一定程度上消除轨道接缝的干扰，但也会导致检测值比实际值偏小，影响控制效果。

由TANH-TD的原理及特性分析可知，跟踪微分器产生的微分信号其实也是原信号滤波之后的“广义导数”；跟踪信号就是对原信号的滤波。根据这些特性，可以对三路间隙信号做如图6所示联合滤波，得到更能接近于实际悬浮间隙的检测值。

图6 联合滤波流程图

设置3组TANH-TD滤波器的参数，使得其在跟踪性能优先的同时完成一定滤波：当某一路悬浮间隙数据明显偏离额定悬浮间隙范围阈值时，可以认为此传感器经过轨道接缝或者出现了故障，此时输出另外两路悬浮间隙数据的均值；当三路悬浮数据均处于额定悬浮间隙要求范围内时，比较三路悬浮间隙微分信号的大小，取微分信号绝对值较小的两路数据的跟踪信号均值。这样的处理过程不会造成综合检测值比实际值偏小的问题，同时相当于又进行了一次滤波过程，达到联合滤波的效果，且消除了悬浮传感器通过轨道接缝时出现的悬浮间隙突变。

以磁浮列车悬浮传感器实测数据(如图7、图8、图9所示)为分析对象，采用上述方法进行仿真验证，然后对传统的悬浮间隙处理方式和本文提出的方法进行对比分析，结果如图10～11所示。

图7 悬浮间隙S1的实测数据

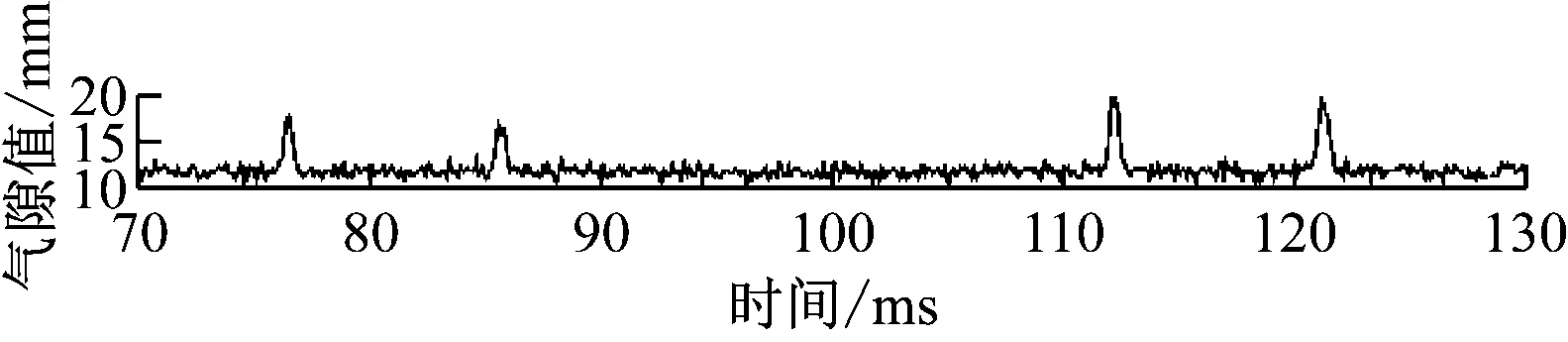
图8 悬浮间隙S2的实测数据

图9 悬浮间隙S3的实测数据

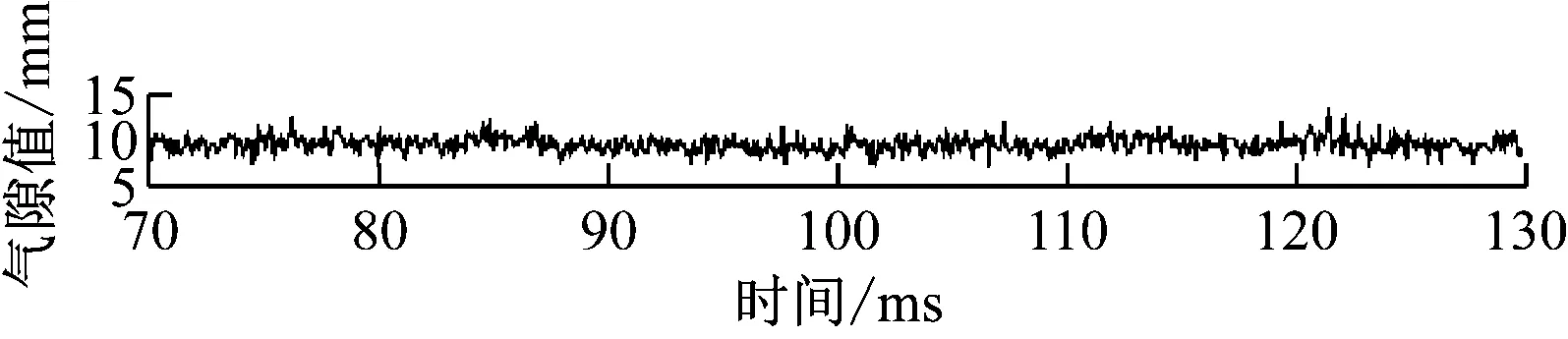
图10 采用传统方法得到的悬浮间隙处理结果

图11 采用本文提出方法得到的悬浮间隙处理结果

由图10～11可见，在悬浮传感器通过轨道接缝时，传统的悬浮间隙处理方式和本文提出的方法均能消除间隙突变。本文提出方法的优势在于：由于跟踪微分器的滤波作用，噪声信号被大幅度降低，处理信号更平稳。另外，当悬浮传感器在通过轨道接缝前后，传统的悬浮间隙处理方式由于直接去掉幅值最大的一组数据，导致传感器未处于过缝时段输出的气隙值小于被控制的真实气隙值12 mm，且在过缝时段(110～125 ms)波动较大；而本文提出的方法可有效避免此情况，获得更好的效果，更有利于悬浮系统的稳定控制。

4 结语

通过理论分析与数值仿真可知，TANH-TD在实际的工程问题中有良好的性能，在消除悬浮传感器过轨道接缝发生信号突变的同时，还可以达到跟踪信号的“二次滤波”，有利于进一步提高磁浮列车悬浮系统的稳定性和可靠性。