锚索桩板墙的结构力学法+m法计算研究

王玉金

（甘肃省交通规划勘察设计院股份有限公司，甘肃 兰州 730000）

0 引言

一般来说，桩板墙中的桩都是抗滑桩，抗滑桩悬臂高度超过12m就应设置锚索，借助锚索提供的锚固力和抗滑桩提供的阻滑力来共同抵抗岩土边坡侧压力或潜在滑坡的下滑推力。锚索的存在极大改善了抗滑桩的受力模型，桩受力状态更合理，通过增设多排锚索，大大减少了抗滑桩的水平位移，特别是桩顶水平位移，使其在工程各领域得到广泛应用，且监测方便，加固简单，质量可控。

1 工程概况

省道104线兰州（沈家坡）至阿干镇段一级公路伏龙坪立交NB匝道BK0+060～230 段路堑位于平面半径75m接39m的两反向S形曲线、纵坡-5.05%接2.95%的凹型竖曲线上，路基宽9.0m，为保留通伏龙坪的上山127县道（伏直公路），新建匝道路基右侧第一级边坡拟设计垂直开挖，最大高度17.3m，开挖土石方约3.1万m3；旧路右侧自然边坡上方分布有居民房屋，坡顶有医院等密集建筑物，拆迁困难，为保证NB匝道及旧路运营安全，拟定锚索桩板墙进行边坡支挡，因此，如何保证路堑边坡体的稳定及锚索桩板墙结构安全是本文的研究重点。

1.1 工程地质条件

该段南北长约200m，边坡高约43m。坡体由黄土状粉土和黄褐色砾砂及黄、红褐色卵石组成，见图1钻孔柱状图。

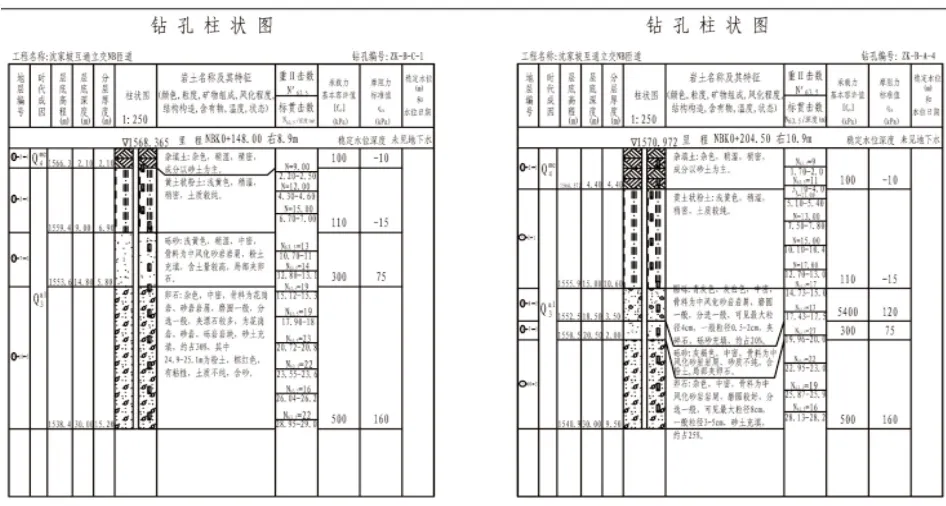
图1 钻孔柱状图

1.2 边坡稳定分析与土压力计算

根据现场调查边坡几何形态，初步判断路基右侧垂直及上方边坡存在整体下滑失稳的潜在危险，滑动面可认为是近似圆弧面，按均匀土层圆弧滑动面计算下滑推力大小。根据该项目沿线地质土工试验数据，以及参考附近已建成通车运营项目连霍国道主干线兰州南绕城高速公路有关地质参数，最终取黄土状粉土粘聚力c=28kPa、内摩擦角φ=26.2度，砾砂粘聚力c=0、内摩擦角φ=30度，卵石粘聚力c=0、内摩擦角φ=36度，容重分别为15kN/m3、19.2kN/m3和22.5kN/m3。该项目为一级公路，且位于人口稠密市郊，正常工况下取边坡稳定安全系数1.3；该地区地震烈度VIII度，根据《公路工程抗震规范》[1]，地震作用重要性系数取1.7，考虑地震作用工况下，边坡稳定安全系数取1.15；运用理正岩土工程计算分析软件搜索出边坡最危险潜在圆弧滑动面（见图2），计算出潜在滑动面的稳定安全系为0.946；如考虑地震工况，则稳定安全系为0.773，均小于1，表明该边坡不稳定，须进行防护。分别计算上述两种工况剩余下滑推力标准值为1647.119kN/m、1824.57kN/m，由此可知，应选择最不利地震作用工况的下滑推力进行结构支挡防护。

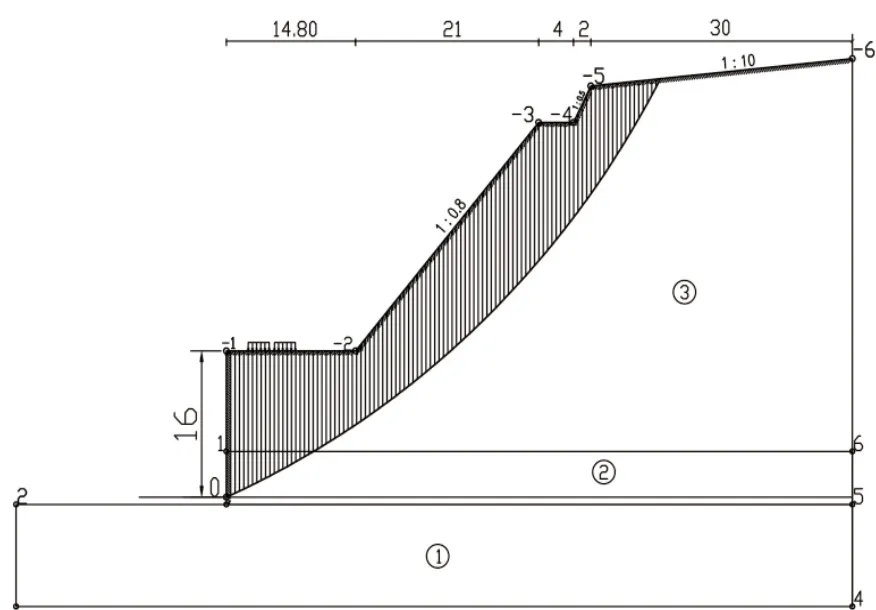
图2 边坡最危险潜在圆弧滑动面

下滑推力分布形式对支挡防护结构的可靠度和经济性影响很大，然而受坡体岩土特性、滑动面形状、地层性质等多因素影响，很难给出准确或统一的推力分布图形。目前，下滑推力分布理论尚不成熟，依然采用工程经验确定：滑坡体上下各层土质较均匀，上部与底部滑动速度相差不大，滑坡推力取梯形分布（上下推力比值取0.8）。

2 方案拟定

该段地形地貌复杂，且位于兰州市区南面通南山坡脚位置，NB匝道平面线位受地形、地物条件严格限制，没有回旋余地，无法进行大开挖，由于拟定抗滑桩悬臂高度达16m，远大于一般值12m，因此最后仅能选择锚索桩板墙结构进行支挡。

2.1 设计资料

NBK0+060～230 段坡体为黄土状粉土覆盖层，路线中心处对应厚度7～13m，下卧卵石层，且NBK0+110～220出现砾砂层，厚度不均，最大厚度5.8m。潜在圆弧滑动面剪出口即为路基挖方边沟底部，桩前部坡体厚度很小，可不考虑被动土压力，则拟设置桩板墙外侧地基系数A1=0、内侧地基系数A2=45(MN/m3)，且滑动面以下桩外侧地基系数呈三角形分布、内侧为梯形分布，由于为卵石土地层，查《公路滑坡防治设计规范》[2]中地基系数随深度增加的比例系数，取水平方向mH=20MN/m4；下滑推力标准值En=1824.57kN/m（与水平方向成24.855°）。

2.2 作用在桩板墙上的力系

作用在桩板墙上的外力包括下滑推力En、锚固段地层抗力（桩侧应力）、桩侧摩阻力和桩底应力等。经验表明，摩擦桩的大部分自重被桩侧摩阻力抵消，因此桩底应力很小，为简化计算且计算偏安全，对桩底应力忽略不计，因此锚索桩板墙实际作用在桩上的外力是下滑推力及桩侧应力、锚索拉力。根据《滑坡防治设计规范》[3]附录C，关于锚索拉力有两种计算方法，考虑到下滑推力大，拟采用设置多道锚索的结构力学法来计算。

2.3 抗滑桩参数

根据路基开挖横断面及自然边坡情况，该段边坡防护设计为悬臂式锚索桩板墙支挡结构。初拟抗滑桩桩身截面尺寸b×h=2.5×3m，桩间距5m，桩长30m，其中受荷段H1=16m，锚固段h0=14m，则桩截面惯性矩I=b×h3/12=2.5×33/12=5.625m4，桩身采用C30 混凝土，弹性模量Ec=3.0×104MPa，则钢筋混凝土桩的弹性模量E=0.8×Ec=2.4×104MPa，桩的抗弯刚度EI=1.35×108kN·m2；矩形抗滑桩的受力宽度换算系数KB=1+1/b=1+1/2.5=1.4，则计算宽度BP=KB×b=1.4×2.5=3.5m，卵石地基按地基系数m法求抗滑桩埋入稳定地层的计算深度。根据上述抗滑桩随深度增加的卵石层地基水平方向的比例系数mH=20000kPa/m2，则桩的变形系数α=(mH×BP/EI)1/5=(20000×3.5/1.35×108)1/5≈0.22027/m，计算深度α×h2=0.22027×14=3.084＞2.5，属于弹性桩。由于锚固段地层为卵石层，虽然胶结密实、强度较高，但整体性和完整性依然不如岩石，再考虑到本抗滑桩悬臂长，为安全起见，抗滑桩的底端按自由端支承处理。

2.4 锚索设计

2.4.1 锚索拟定

由以上分析可知，锚索桩承受下滑推力大，初步拟定设置三排锚索，每排锚索采用7×7φS152.2-1320-GB/T 5224-2014，根据理正软件搜索出潜在圆弧滑动面位置，通过地质横断面布置锚索，见图3。

图3 锚索横断面布置图

将自由段超过潜在滑动面及砾砂层2m，锚入胶结密实的卵石层内，可得自由段长度：LS1=32.5m，LS2=26.5m，LS3=19.5m，则对应第i根锚索水平方向的弹性系数：

Ki=ESASicosα/LSicosα=ESASi/LSi

式中，ES—锚索弹性模量，取1.95×108kPa；ASi—第i根锚索的截面面积，ASi=7×140=980mm2；LSi—第i根锚（索）杆自由段长度。取锚索下倾角为20o，K1=1.95×108×980×10-6/32.5=5880kN/m，K2=7211.32kN/m，k3=9800kN/m。

2.4.2 锚索拉力计算

依据《滑坡防治设计规范》[3]附录C.2，采用结构力学公式A·X+AP=0，计算锚索水平拉力。其中，3×3阶锚索点处的单位变位系数矩阵A、3×1阶载变位系数列阵AP、3×1阶锚索拉力TA在水平方向上的分力列阵X分别如下：

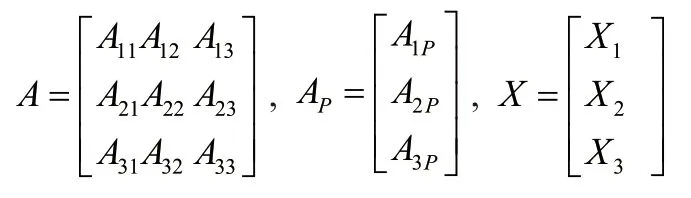
2.4.2.1 单位变位δij计算

要求锚索点处的单位变位系数Aij，需先求出该锚索点处桩的单位变位δij，当i，j分别取1、2、3，对应的锚索作用点距离滑面的距离L1=15m，L2=12m，L3=9m，得到桩的单位变位：δ12=L22(3L1-L2)/6EI=144(3×15-12)/6×1.35×108=5.86667×10-6m/kN，δ13=3.6×10-6m/kN，δ21=5.83333×10-6m/kN，δ23=2.7×10-6m/kN，δ31=3.33333×10-6m/kN，δ32=2.66667×10-6m/kN。

当j=i=1 或2 或3 时，对应的锚索作用点距离滑面的距离L1=15m、L2=12m、L3=9m，则按δii=Li2(3Li-Li)/6EI=Li3/3EI 计算对应桩的单位变位δ11=L13/3 EI=153/3×1.35×108=8.33333×10-6m/kN；δ22=4.26667×10-6m/kN；δ33=1.8×10-6m/kN。

锚固段桩顶作用单位力和单位力矩时分别引起锚固段桩顶的水平位移、角变位，可将Q0=1，M0=1分别代入公式（1）、（2）计算：

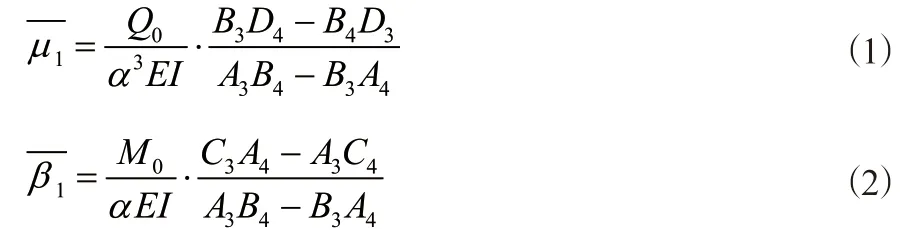
2.4.2.3 单位变位系数Aij

①当i≠j时，可按下式计算桩锚索点处的力法方程对应的变位系数，得：

②当i=j时，可按下式计算桩锚索点处的力法方程对应的变位系数得：6.05208×10-8)+1.85067×10-6+5880-1=0.000166635m/kN，A22=0.000136073m/kN，A33=0.000100789m/kN。

2.4.2.4 桩的载变位ΔiP

取桩间距5m，则每根桩和锚索共同承受的下滑水平推力标准值Er=5En×cosθ=5×1824.57×cos24.855°=8277.8 4kN，根据《公路路基设计规范》[4]潜在滑动面下滑推力可以理解为土侧压力，属永久荷载，其荷载分项系数取1.35，则下滑水平推力设计值P=8277.84×1.35=11175.08kN，桩的载变位可由△iP=-Ph02(3Li-h0)6EI式计算，其中，h0为桩悬臂段土下滑推力合力作用距滑动面的距离，经计算y1=7.7m，则△1P=-Ph02(3L1-h0)6EI=-11175.08×7.72(3×15-7.7)/6×1.35×108=-0.030510973m，△2P=-0.023149076m，△3P=-0.015787179m。由于滑坡推力P在嵌固段桩顶产生的力矩MOP=11175.08×7.7=86048.12kN·m、产 生的剪力QOP=P=11175.08kN，则对应桩的载变位系数可由 公 式计 算，A1P=△1P+L1MOP=-0.030510973+15×89048.12×(-6.05208×10-8)+1.85067×10-6=-0.108624644m，A2P=-0.085639643m，A3P=-0.062654641m。

综上可得：

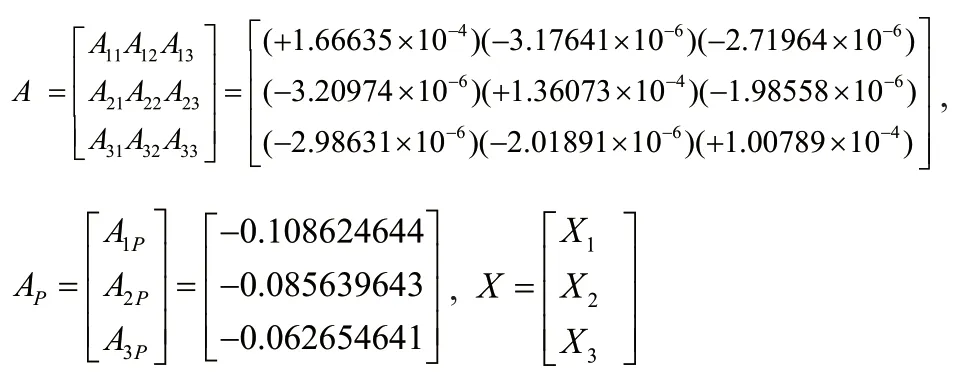
代入公式A·X+AP=0，用行列式解法计算得各锚索水平拉力标准值X1=544.46kN，X2=496.69kN，X3=442.55kN，则锚索水平拉力的合力X=X1+X2+X3=54 4.46+496.69+442.55=1483.7kN，与潜在下滑推力的比值1483.7/11175.08=13.3%，比值太小。考虑到本项目下滑推力大，又位于兰州市主城区旁，一方面安全性要求高（安全冗余度大），另一方面抗滑桩要适度美观（外形尺寸不宜过大），因此，可适当增加锚索截面积，使其分担的下滑推力在其承载能力范围内尽可能大（即增大锚索拉力），也可根据抗滑桩地基横向承载力或桩顶及锚固点水平位移值满足规范要求来估算锚索截面积，重新拟定锚索为9×7φS21.6-1320-GB/T 5224-2014，则单根锚索截面面积ASi=9×285=2565mm2，重复上述计算过程求得各锚索水 平 拉 力X1=1561.35kN，X2=1440.52kN，X3=1313.01kN，则此时锚索水平拉力的合力X=X1+X2+X3=1561.35+144 0.52+1313.01=4314.88kN，与潜在下滑推力的水平分力比值4314.88/11175.08=38.6%，比值提高了一倍多，可继续下一步计算锚索拉力设计值：T1=X1/cosα=1561.35/cos20≈1661.55kN，T2=X2/cosα=1440.52/cos20≈1532.97kN，T3=X3/cosα=1313.01/cos20≈1397.28kN。

该值虽然大于《建筑边坡工程技术规范》[5]轴向拉力标准值800kN（转换成设计值1080kN）较多，但考虑到本边坡锚固段土质为胶结密实的卵石层，且地层干燥，其标贯数N63.5 平均值在20～30 范围内，又参考美国PTI 1996 年制定的《岩层与土体预应力锚杆的建议》中密实至极密的砂砾石与砂浆锚固体的平均极限粘结应力达到0.28～1.38MPa，经估算，锚固力应超过土质达到软质岩的程度或可采取扩大锚头直径增大锚固力（轴拉力）。

2.4.3 锚索验算

2.4.3.1 预应力钢绞线根数

上述计算中单根钢绞线初步拟定为1×7φS21.6(设计抗拉强度fpy=1320MPa)，则单根钢绞线的设计最大拉力Fm=fpyAS1=1320×285=376200N；锚具效率系数ηm=0.95、锚索根数n=9；锚索抗拔安全系数Fb=nηmFm/Tk=9×0.95×376.2/1661.55≈1.94，满足锚索材料抗拔安全系数范围1.8～2.2，即锚索根数初步验算合理。

2.4.3.2 锚索锚固段长度

①锚索与注浆体的锚固长度

根据《滑坡防治设计规范》[3]，设计采用42.5MPa水泥、按照水灰比0.45配制的水泥砂浆构成注浆锚固体，依据下式计算锚索与注浆体的锚固长度：

La≥FbTk/nπdfms

式中，Fb—锚索钢绞线与注浆锚固体抗拔安全系数范围2.2～2.6，取Fb=2.6；fms—枣核状钢绞线界面与水泥砂浆注浆体间粘结强度设计值，取3MPa；d—单根钢绞线公称直径，取21.6mm；n—钢绞线根数，9根。La≥FbTk/nπdfms=2.6×1661.55/9π×21.6×3≈2.36m。

②注浆体与锚孔胶结卵石层的锚固长度

同理，根据《滑坡防治设计规范》[3]，锚索锚固段拟定钻孔直径D=350mm，依据下式计算注浆锚固段与锚孔胶结卵石层的锚固长度：

La≥FbTk/πDfmg

式中，Fb—注浆锚固体与胶结卵石层锚孔壁抗拔安全系数范围2.2～2.6，取Fb=2.4；fmg—注浆锚固体与胶结卵石层锚孔孔壁间极限粘结强度标准值，锚固段采用二次压力注浆，取0.36MPa；D—钻孔直径，取350mm。La≥FbTk/πDfmg=2.4×1661.55/π350×0.36≈10.08m。

综上，锚索锚固段长度La=max[2.36，10.08]=10.08m，取整数10m。

2.4.4 受荷段桩身内力计算

最不利滑动面以上抗滑桩受荷段上所有的力均当作外荷载看待，由于滑面以上桩前无抗力，因此仅把剩余下滑推力折算到滑动面上的弯矩和剪力作为锚固段的外荷载，而抗滑桩的锚固段则把桩周卵石层视为弹性体计算侧向应力（土抗力），从而计算锚固段桩的内力。由上述计算可知，剩余下滑推力设计值P=8277.84×1.35=11175.08kN，又根据边坡土层性质、力学性能等，下滑推力呈梯形分布，初步拟定桩顶下滑推力P1与桩滑动面处下滑推力P0的比值取0.8，如图4，计算得P1=620.84kN，P0=776.05kN，则抗滑桩潜在滑面以上受荷段桩身各截面剪力和弯矩的计算结果见表1。

图4 受荷段桩身内力计算图

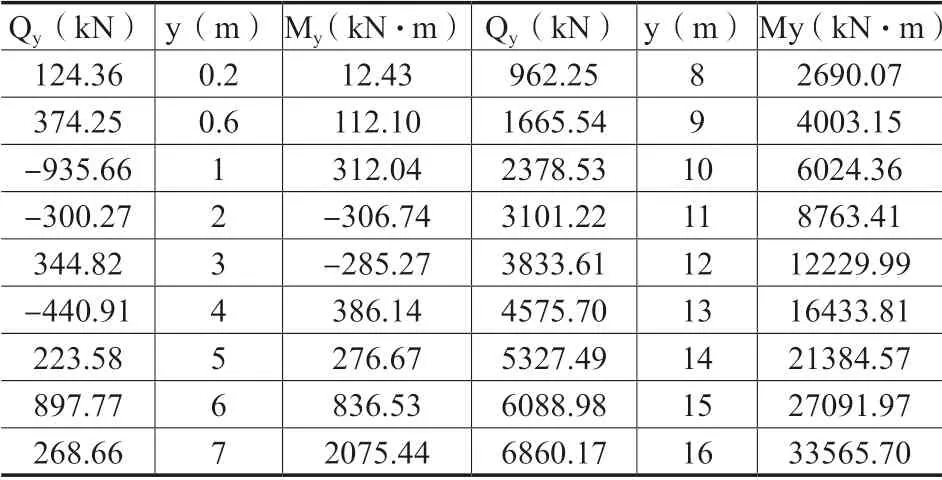
表1 受荷段桩身剪力和弯矩

由表1可知，滑动面处的剪力和弯矩分别为Q0=6860.17kN，M0=33565.70kN·m，且下滑推力合力P作用点距桩底y1=298 00.32×16+155.21×162/59600.64+465.63×16≈7.7m。

2.4.5 锚固段桩身内力计算

该抗滑桩判断为弹性桩，表明埋于卵石地基部分的锚固段受力后桩轴和桩周卵石土均发生变形，将桩简化成图5弹性桩，根据卵石地层性质确定地基抗力系数，即采用m法、由滑面处桩外侧地基系数等于零，建立抗滑桩的挠曲微分方程[6]：EIdx4/dy4+mHyBPx=0。

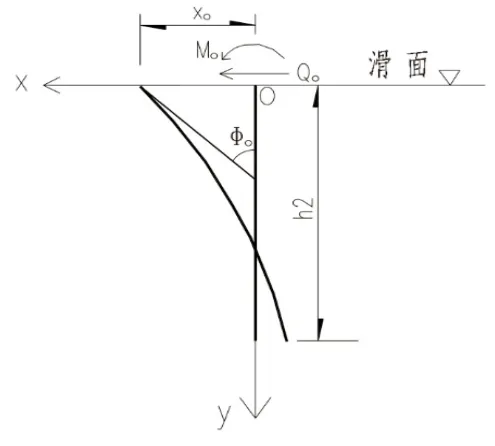
图5 弹性桩计算图

这是一个四阶线性变系数齐次微分方程，用幂级数展开后进行近似求解，换算整理后得锚固段任意y处桩身的剪力和弯矩：

卵石地基桩底按自由端支承考虑，桩底弯矩MB=0、剪力QB=0，计算滑动面处弯矩设计值M0和剪力设计值Q0，代入得桩锚固段桩身任意位置的剪力和弯矩设计值，见表2。

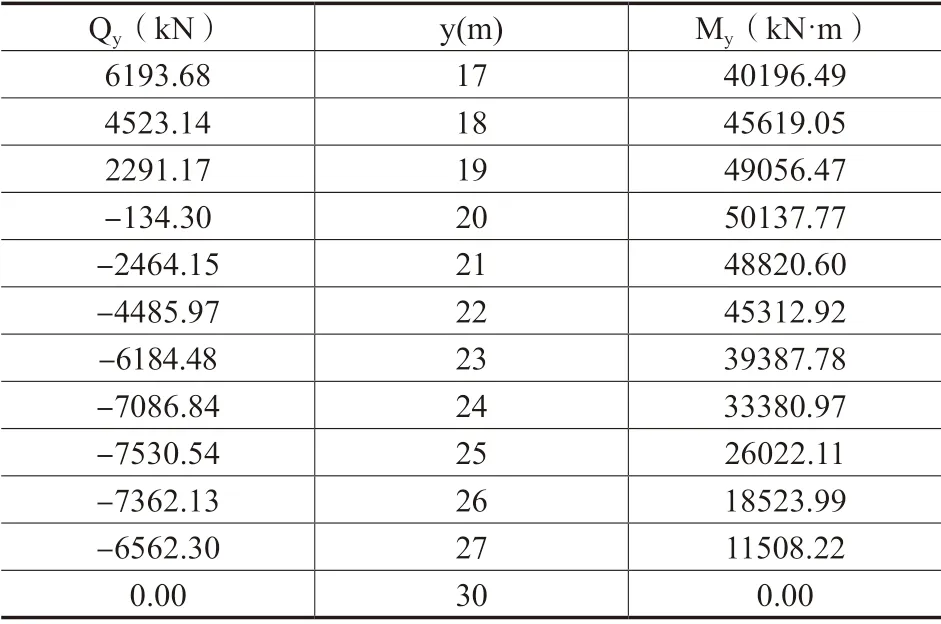
表2 锚固段桩身的剪力与弯矩设计值

试算后y=20m 时，取得最大弯矩设计值Mmax=50137.77kN·m，y=25m时，取得最大剪力Qmax=-7530.54kN(负号表示与上部土压力方向相反)。

2.4.6 锚固段桩侧应力

2.4.6.1 锚固段桩侧位移计算

根据上述四阶线性微分方程，用幂级数展开后可求得锚固段桩身距滑动面任意距离y处水平位移近似解：

2.4.6.2 锚固段桩侧应力计算

由于桩前为行车道，汽车荷载较小，可不考虑荷载对桩前锚固段地基系数的影响，即桩前滑动面处抗力为零（A0=0），桩前滑动面以下地基系数my呈线性变化，即my=mH·y=2×104y，则弹性桩桩侧应力σy=myxy=2×104y·xy，其中，xy为上述计算的桩侧水平位移，由此可计算锚固段任意位置的桩侧应力σy。

2.4.6.3 锚固段地基强度校核

锚索桩顶为县道127线伏直公路，其包括边沟、碎落台等空余宽度约9～15m不等、横坡较小；桩滑动面以下为卵石土层（胶结好），桩在侧向土层下滑推力作用下发生转动变形，滑动面以下桩前卵石土层产生被动土压力，而滑动面以上桩后土层产生主动土压力，锚固段桩身对地基主体的侧向压应力σy一般不应大于被动土压力与主动土压力之差，根据《建筑边坡工程技术规范》[5]，本抗滑桩处沿滑动方向地面坡度小于8度，锚固段地基任意y点的横向允许承载力[σH]=4γ2ytanΦ0/cosΦ0-γ1h1(1-sinΦ0)/(1+sinΦ0)，式中，[σH]—地基横向容许承载力kPa；0φ-滑动面以下卵石土层等效内摩擦角，由于卵石层C=0，因此 0φ=φ=36o；γ1-滑动面以上土体的重度，加权平均后为18.11kN/m3；γ2-滑动面以下土体的重度，22.5kN/m3；h1-设桩处滑面至地面的距离，取16m；y-滑动面至桩滑动面以下任意点的距离，m。由此可计算滑动面以下桩任意点的地基横向容许承载力并进行校核，结果见表3。

表3 锚固段桩身地基横向承载力及校核

计算表明，锚固段16～22m长度范围桩侧应力均小于卵石地基的横向容许承载力，不满足《滑坡防治设计规范》[3]中对土层地基在滑动面以下深度h2/3处的横向压应力应小于或等于地基横向容许承载力的规定，因此必须调整桩截面尺寸或埋深，又考虑到桩截面尺寸与周围环境已协调匹配，因此将埋深14m调整为16m，再次计算得σh2/3=604.504kPa，远大于地基横向容许承载力301.957kPa，说明通过增加埋深的办法无法满足地基横向承载力要求。通过分析发现，滑动面处的弯矩、剪力太大是导致滑动面处水平位移x0过大，进而造成地基横向承载力不足的主要原因，因此，重新拟定锚索为12×7φS21.6-1320-GB/T 5224-2014，则单根锚索截面面积ASi= 12 × 285 =3420mm2，重复上述计算过程求得各锚索水平拉力:T1=2338.4kN，T2=2170.5kN，T3=2002.1kN；滑动面以下深度为h2/3处的横向压应力h2/3=423.97kPa，亦大于地基横向容许承载力301.957kPa，且锚索拉力值太大会导致锚索锚固段太长或孔径太大，造成施工困难，钻孔费用高、不经济，因此该改进措施也不可行。但可以发现，单孔锚索根数由9 根增加到12 根，锚索拉力增大了40.7%、滑动面以下深度h2/3处的横向压应力σh2/3减小了约35.5%，效果明显，虽然最终仍不满足地基横向容许承载力要求，但差值已不大，这时通过调整桩间距由5m缩减至4m（即下滑推力减小1824.57kN），并将第二、三排每孔锚索根数增加至13根，重复上述计算过程得σh2/3=287.67kPa，满足小于地基横向容许承载力301.957kPa要求，这时各锚索拉力Td1=1891.75kN，Td2=1903.2kN，Td3=1757.14kN，核查锚索抗拔安全系数Fb=nηmFm/Tk=12×0.95×376.2/1891.75≈2.27，满足锚索材料抗拔安全系数范围1.8～2.2 范围，单锚孔钢绞线根数n取12（13）根是合理的。根据《建筑边坡工程技术规范》[5]，锚索锚固段长度aL取最大值10m，并满足公式La≥FbTk/πDfmg时，计算钻孔直径D，La≥FbTk/πDfmg=2.4×1903.2/π10×0.36≈404m；因此最终取钻孔直径D=40.5cm。另外，经试算几种桩截面尺寸(2.2×2.8，2.2×2.6，2×2.5，2×2.4)，并和不同锚索类型进行组合，发现既满足地基横向容许承载力，又满足锚索抗拔安全系数要求，还要考虑施工难易程度的要求，只有桩截面尺寸2.5×3、最上排锚孔锚索12×7φS21.6、中间和最下排锚孔锚索13×7φS21.6，此时滑动面以下4.6m桩范围的地基出现允许的塑性变形，4.6～桩底范围地基横向为弹性变形，这样最终确定了桩截面尺寸、桩间距和锚索类型。

3 桩的校核

3.1 桩的位移校核

参见《新型支挡结构》[7]中滑动面以上悬臂式抗滑桩滑坡推力梯形分布的水平位移计算，得出悬臂式抗滑桩桩顶最大水平位移xy=0.07m，显然小于《滑坡防治设计规范》[3]中悬臂式抗滑桩顶水平位移一般值100mm。本项目桩滑动面位于桩h1=16m处，而该点水平位移为x0=8.44mm，小于《滑坡防治设计规范》[3]规定的最大值10mm，满足规范要求，桩的位移校核通过。

3.2 桩承载力校核

根据上述重新拟定的桩间距、锚索面积下桩悬臂段、锚固段任意y处桩身内侧剪力和弯矩设计值，计算结果Qmax=3722.79kN(y=16m)，Mmax=16672.51kN·m(y=21m)；桩外侧最大弯矩M′max=-5556.06kN·m，拟定桩受压侧钢筋，并取桩的钢筋保护层厚度80mm，通过计算桩截面混凝土受压区高度x，并利用公式计算出受拉侧钢筋面积，配置HRB400 钢筋四肢箍4φ20@300，并利用公式，容易检算出桩的内外侧正截面受弯承载力、斜截面受剪承载力满足《混凝土设计规范》[8]要求。

3.3 桩抗裂校核

由于本路堑边坡无腐蚀性，可不验算桩的裂缝宽度，采用构造措施（钢筋保护层厚度80mm）即可。由于板的计算比较简单，这里不再赘述。

4 结语

经过上述锚索桩板墙整个支挡防护方案的计算过程及分析可知，锚索桩板墙的计算量大、过程复杂，主要包括下滑推力计算、锚索拉力计算、桩身内力计算、桩锚固地基横向承载力计算、桩顶及桩锚固点位移验算、桩配筋及承载力计算以及桩抗裂验算；且锚索桩板墙计算时受到的影响因素多，主要有地基系数m的确定、土体自身抗剪参数c、φ值、钢筋和钢绞线类型选择、锚孔岩土体与砂浆锚固体间粘结强度、钻孔机械能力大小等。本锚索桩板墙由于悬臂高度大，经反复计算，最终确定合理的设计方案，为工程提供了可靠的安全保障。目前，该工程已顺利完工，未发现桩顶127县道及山体有任何滑移变形，保证了路堑边坡稳定，达到了工程预期效果。