基于单目多视立体几何的对象三维重建方法研究*

赵柏山，张力华

（沈阳工业大学，辽宁 沈阳 110870）

0 引言

在计算机视觉技术中，三维重建是目前最为热门的研究方向。利用计算机建立表达客观景物的三维模型，以此来满足生产和生活的需要，在医学治疗、文物保护、航天航海等诸多领域有着广泛的应用，对三维场景进行高精确的重建意义重大。

近年来，基于特征点的方法在场景三维重建领域已经取得了一定的成果，但仍受制于复杂条件下特征提取的质量的影响，存在一些不可忽视的弊端：①由于图像特征的局部特性，误匹配的情况广泛存在，目前已经成为图像重建中性能提升的一大瓶颈；②环境的多变性使检测到的特征不稳定，不同天气，同一建筑物同一角度提取到的特征可能不同，导致特征提取及匹配精度降低，影响重建的精度甚至重建失败，大大降低了传统的三维重建的泛化性能；③传统的三维重建采用的特征主要是低层特征如特征点、线等，然而图像中的物体对象作为环境中的重要组成部分，在三维重建中还没有被利用。

针对上述问题，本文提出一种基于立体几何的将低层像素级图像特征点、线等与高层物体级别图像特征对象归一到一个构架下的方法，实现几何信息和语义信息级联的多视图三维对象重建模型。加强了几何约束和尺度一致性，提高了相机位姿估计及目标场景重建精度。

1 多视图三维对象重建原理

设三维空间点P，通过刚体变换到二维平面的像素坐标为：

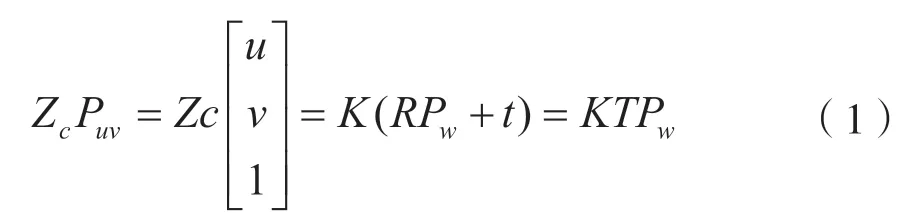
式中，Pw是点P在世界坐标系下的坐标表示，Pw=[Xw,Yw,Zw]T，Pc是点P在相机坐标系下的坐标表示，Pc=[Xc,Yc,Zc]T,世界坐标系与相机坐标系之间相差一个3×3的旋转矩阵R和一个3×1的平移向量t，其关系为：

在针孔相机模型下，将三维空间点P投影到物理成像平面上，得到像点在图像坐标系下的坐标为p=[x,y]T：

转换到其次坐标系下将其线性化，如下：

f为相机的焦点到成像平面的距离，即焦距。

上述的像点坐标p=[x,y]T在成像平面坐标系下，式（4）描述了三维空间点P和它的像之间的空间关系。实际上，实际像素点的表达方式是以像素来描述的，即将图像数字化。

像素坐标系u轴向右与x轴平行，v轴向下与y轴平行。像素坐标在u轴上缩放了α倍，在v轴上缩放了β倍，原点平移了(cx,cy)T，将像点坐标(x,y)转换为像素坐标(u,v)为：

将上面求得的(x,y)带入式（3）可得到：

其中，fx=α·f，fy=β·f

转换成其次坐标形式：

根据式（2）、式（4）和式（7），即得式（1）的展开形式：

同一个空间点P在多视角图像上进行投影，如果知道这些来自于同一个空间点的像素点的位置信息，利用对极几何及三角测量原理[4]即可推断出P的空间位置以及相机的运动。

2 多视图三维对象重建方法框架

本文在传统的运动恢复结构的重建框架上进行改进，通过ORB角点提取的方式获得前两幅图像的关键点，接着在对特征点进行有效提取后进行特征选择，将特征提取[6]步骤中无用特征及不敏感特征进行筛选，进一步缩减误匹配特征数量，从而缩短重建时间，提高重建效率。除了点特征，还引入了三维目标检测改善点特征不稳定问题，将对象提供的几何约束和语义约束加以利用，从而改善相机位姿，进一步提高重建质量。接着进行数据关联，引入了对象特征后，帧与帧之间除了原有的点与点匹配，还多了点与对象匹配，以及对象与对象匹配。

由于存在许多误匹配现象，于是接着通过随机采样一致性RANSAC算法来消除这些错误匹配的点，最终得到每幅图像点与点、点与对象、对象与对象的匹配关系。在知道了相机的运动之后，通过三角测量估计特征点的空间位置，从而进行图像间的三维重建，并通过光束法平差（bundle adjustment，BA）[7]算法来降低噪声的影响，从而对重建结果进行优化。

本文算法的各个阶段如图1所示，蓝色和橙色为原来的单目SFM方法部分，绿色为SFM方法基础上新增的两个部分，加入三维目标检测以及特征点再剔除之后，橙色部分数据关联、消除误匹配以及BA优化结果都有一定的改动，使得重建结果精度更高，普适性更好。本文方法由如下4部分构成。

（1）原来的单目SFM方法以及改进：同时进行特征点检测与三维目标检测。

（2）特征再剔除算法：将上一阶段得到的特征点进行筛选，删掉无用及不敏感特征，进一步缩减无效特征数量。

（3）数据关联：除了原始的点与点之间的数据关联，还多了点与对象以及对象与对象之间的数据关联。

（4）三维对象重建算法：通过匹配各个关键帧中提取到的特征点及对象来重建场景的三维模型。

图1 三维重建算法流程图

3 特征点检测匹配与三维目标检测

3.1 特征点检测

三维重建需要获取三维空间中的特征点在不同成像平面上的投影点对。特征点反映图像的本质特征，由关键点和描述子两部分组成，关键点是提取到的关键，而描述子则是将这些关键点彼此之间匹配上的关键。

特征点检测与匹配流程图如图2所示。迄今为止，研究者们提出了许多图像特征，其中Harris、Fast、SIFT、SURF以及ORB[8]当属最为经典的几种。本文需要对多帧图像进行三维重建，因此需综合考虑特征提取的重复度、数量和复杂度。ORB在保持了旋转、尺度不变性的同时，速度方面有明显提升，在质量与性能之间有较好的折中，本文特征检测部分选择ORB算法来做。

3.2 三维目标检测

本文三维目标检测部分主要是通过平面的二维目标检测框生成立体的三维立方体包围盒，生成的三维立方体包围盒带有9个参数，分别是三维的位置信息(tx,ty,tz)、三维的旋转矩阵R以及三维的尺度信息(dx,dy,dz)。由于三维立方体有3个正交轴，根据旋转矩阵R和相机参数K，通过透视投影可生成三个消失点。故可以通过估计物体的3个自由度旋转矩阵R来计算消失点，并在立方体的上边缘采样一个角点，之后结合3个消失点分析计算其他7个角点。

图2 特征点检测与匹配流程图

3.3 特征点过滤

为了提高特征点的抗噪性能和特征匹配的正确率，提出一种将对比度低，稳定性不强的特征点进行过滤的机制，上文最终以ORB算法进行特征提取，于是筛选的依据就是如若描述子之间的汉明距离小于所有配对的描述子的最小距离的两倍，则认为匹配有误，将其过滤掉，同时设置一个经验值，本文设置为30，以防最小距离过小。

3.4 跨帧的数据关联

过滤后的特征点可以通过暴力匹配[9]（Brute-Force Matcher）进行特征匹配。上文采用了ORB特征，即用的是BRIEF描述子，那么这里用汉明距离（Hamming Distance）作为度量，这即为点与点之间的数据关联。

点和对象之间如若观察到的点属于物体的二维边界框内，并且与三维空间中的立方体的质心的距离小于一定阈值（本文根据数据源将此数值设置为1 m），则认为该点属于该对象。

如若不同帧之间的对象具有最多的共享特征点，并且共享特征点数量超过某个阈值（本文设置为10），则将这两个对象进行数据关联。

3.5 实验结果及分析

图3（a）和图3（b）为多个视角所拍摄的原始图像之中的两张，图3（c）为采用ORB算法所提取到的特征点，图3（d）为用ORB算法进行特征匹配，有很多误匹配，因此图3（e）为采用RANSAC算法去除误匹配的结果，图3（f）为对象三维检测结果。可以看到，对象未检测之前，所提取到的特征点极少，这导致重建失败，但通过特征点的提取和三维对象检测后，如图4所示，生成只有对象的稀疏点云，而且是相对稠密的稀疏重建，解决了因特征较少重建失败的问题。

图3 特征检测与匹配结果及三维目标检测结果

图4 三维对象重建结果

4 结论

本文从传统的基于特征点的运动恢复结构法三维重建分析入手，研究了基于多视立体几何的特征点法与三维目标检测方法相结合的三维重建，并通过实际的实验室设备验证了该方法的有效性。利用三维目标检测以及RANSAC算法很好地改进了ORB进行特征提取与匹配，并在此基础上计算点云，最后实现了稀疏重建。实验结果表明，利用该方法可以有效的避免由于低级纹理特征受光线等影响以及提取不到特征而重建失败的情况，具有较好的重建效果，验证了低级纹理特征点与高级对象特征有效结合进行重建的应用鲁棒性好，实时性强。