三维建筑模型的规则化重构方法
陈佳舟,陆鹏飞,徐阳辉,王宇航,金灵枫,2,李凯勇,秦绪佳
1(浙江工业大学 计算机科学与技术学院,杭州 310012) 2(东南数字经济发展研究院 数字空间技术研发中心,浙江 衢州 324000) 3(青海民族大学 物理与电子信息工程学院,青海 西宁 810007)
1 引 言
随着无人机的普及,倾斜摄影测量技术在测绘领域得到广泛应用.该技术利用图形学中的Structure of Motion(SfM)和Multi-View Stereo(MVS)方法[1-3],通过多组无人机航拍照片重建出高精度三维城市模型,极大地推动着智慧城市的发展.典型的SfM和MVS方法首先自动提取和匹配输入图像几何每个像素点之间的特征,然后恢复出图片的内部和外部摄像机参数,再由像素点对生成密集的3D点云模型,最后重建网格并贴上纹理.
虽然倾斜摄影测量技术能够重建出大规模逼真的三维城市建筑,但这些模型在城市规划、安防、GIS系统、虚拟现实和建筑设计等领域却难以广泛应用.其中一个重要的原因是倾斜摄影测量技术自动构建的三维建筑网格模型顶点数量庞大、噪声多,给数据存储、传输以及语义表达等诸多方面带来了难以逾越的障碍.
三维网格模型的规则化重构(部分论文中译为三维模型的简化,下文出现的模型简化即规则化重构),是解决上述顶点数量爆炸和噪声多问题的重要途径之一.SketchUp的Pointools插件(1)http://www.pointools.com/pointools-plug-in-for-sketchup.php,2019.允许用户直接在3D点云上进行简化,但简化的准确性依赖于用户的熟练程度.用户需要通过目视检查是否手动将简化后几何线条对准了模型中相应的点云.由于点云模型中存在固有的噪声,用户还需通过手动移动边缘点来封闭简化过程中出现的间隙,效率较低.此类简化算法[4-7]通过提供用户界面以手动的方式简化模型,但简化的准确性依赖于用户的技术和耐心.大量半自动[8-13]和全自动[14-18]的简化系统在近年来取得了一定成效,但半自动系统需要过多的人工干预,而全自动系统不是依赖先验信息(图像和视频等),就是对待简化模型有着严格的假设,难以大范围推广.比如,Chen和Chen提出了一种通过在图中搜索哈密顿回路来简化模型多边形表面的方法[12].该方法的前提是假设存在完整的平面集及其相邻信息.如果两个平面对应点集之间的最小距离在一定距离阈值内,则判断它们是相邻的.由于现实数据普遍存在数据错误和缺失,所以需要更复杂的算法来解决此问题.最近,Nan等人提出了一个PolyFit系统[16],首先通过改进的RANSAC聚类方法进行点云的聚类,然后用聚类出的结果将模型切割成小块的平面,再规则化提取出的平面,最后将问题转化为二进制标记问题选出适合的候选平面,从而拟合出简化结果.然而,该方法对点云模型的精度要求较高,对粗糙建筑模型的鲁棒性较低.因此,三维建筑网格模型的规则化重构是一个亟需解决但又充满挑战的课题,一直都是计算机图形学领域的热点问题.
与地面激光或雷达不同,无人机拍摄是在低空自上而下完成的,无人机照片中屋顶的可见性较高,而建筑底部的可见性通常较低.因此,基于倾斜摄影测量重建的三维建筑模型往往屋顶比较精确;底部由于相互遮挡和其他建筑物干扰等原因,重建精度远远低于建筑顶部.基于上述观察,本文提出了一种基于屋顶轮廓线的三维建筑模型规则化重构方法.首先,分割屋顶并提取屋顶的外轮廓线,进行化简并规则化;接着,通过改进的平面拟合提取屋顶的内轮廓线;然后,根据屋顶内外轮廓线进一步组合优化拟合出屋顶平面几何基元;最后,针对屋顶中的非平面部分(太阳能、烟囱等),进行补充规则化处理.
本文方法无需借助任何其他先验信息,能够自动地将粗糙的三维建筑模型重构为少量三角面片组成的规则化三维模型,数据量平均极大减少(仅为原始模型的0.25%).大量的实验表明,本文方法具有效率高、稳定性好等优点,有助于打通倾斜摄影测量到智慧城市应用的最后一个数据障碍.
2 算法设计
本文方法将倾斜摄影测量重建的三维建筑网格模型作为输入,主要研究目标是将三维模型自动重构为规则化的简化模型.如图1所示,本文方法主要分为3个步骤:屋顶面外轮廓线提取与精化、屋顶面内轮廓线提取、规则化模型的生成.其中,外轮廓提取与精化和内轮廓线提取为规则化模型的生成提供了重要的基本元素,而重构后的规则化三维模型则是整个算法的最终成果.

图1 算法流程图Fig.1 Overview of our method
2.1 屋顶面外轮廓线提取与精化
针对单幢三维网格建筑物模型,本文首先进行预处理,提取出属于屋顶面的三角面片.具体而言,将面片高度大于h,且面片法向量与地面法向量夹角小于θ的三角面片视作屋顶面片.h在本文中可自由调整,一般取1/2建筑物高度的值;θ取20度.需要指出的是,这两个参数对本文方法的结果影响很小,少量立面部件(如太阳能)未被提取并不影响外轮廓线的生成,且在非平面基元提取部分进行补充处理.本文所有实验均取上述两个数值.图1左图为本论文需要规则化重构的原始三维建筑模型,图1所示的屋顶面外轮廓线提取与精化部分左图中的白色部分为预处理所提取出的屋顶面片.
在提取完屋顶面片后,提取屋顶面外轮廓线.通过三角面片的邻接关系提取屋顶面外轮廓线是一种普遍的三角面片轮廓线提取方法,但该方法容易将断裂的内轮廓误判为外轮廓,使屋顶内部有一部分点被错误地提取为边缘点.本文采用Alpha Shapes[19]方法来解决这一问题.该方法是一种有效的恢复离散点集原始形状的轮廓线提取算法,提取过程等同于用一个半径为α的圆在点集周围滚动.只要参数α足够大,圆只会在点集外部滚动,不会进入点集内部引起断裂.在本文所有实验中,α取3米.
经过Alpha Shapes方法提取出来的轮廓线段往往非常粗糙(图2左图),一般需要进一步对其进行简化处理.本文提出了一种基于最小平方法的轮廓线化简方法,详细设计步骤如算法1所示.该方法需要两个参数,即点到直线的最大距离阈值d和最小直线长度阈值l.在本论文中,d一般设置为0.5倍的平均点间距,l设置为3倍的平均点间距.

图2 外轮廓线提取过程Fig.2 Extraction process of outer-contours
算法1.
输入:按序排列的外轮廓二维点集US.
输出:按序排列的经过简化后的二维点集.
Step 1.按顺序依次选取轮廓线上US的3个连续的顶点a、b、c,并且用最小平方法拟合出经过这3个顶点的一条直线L,计算3个顶点到直线L的距离,如果任意一个顶点到直线L的距离大于阈值d,则下一步转到Step 4;否则,令集合U={a,b,c},转Step 2;
Step 2.取集合U两端点作为p和q,分别以p和q作为起点向两侧进行延伸,延伸过程中会遇到新的顶点,如果新的顶点到直线L的距离小于阈值d,则将其加入到集合U中,并将其作为新的端点,转Step 3;
Step 3.在Step 2中,如果存在新的顶点被加入集合U中,则对集合U中的所有顶点用最小平方法重新拟合一条直线L,转Step 2;否则,转Step 4;
Step 4.判断集合U拟合出的直线的长度,若直线长度大于阈值l,则将集合U两端的顶点保留,舍弃中间的顶点,转Step 5;否则,舍弃所有的顶点,转Step 5;
Step 5.如果还有连续的3个顶点没有判断过,则转Step 1;否则,结束算法.
图2中图是最小平方法的轮廓线化简算法的结果.建筑物通常具有相对规则的几何形状,因此,针对建筑物外轮廓线的规则化应充分考虑垂直和平行这两个最基本的特征,本文通过提出的分类强制正交规则化方法进行处理.具体方法是找出最长的线段为初始线段,其他线段与之判断,若两线段方位角的差在阈值范围内,则归为A类,否则归到B类;然后根据每类线段的长度加权平均方位角调整每一条线段,计算出线段的新端点,即保持A类线段平均方位角不变,将B类线段平均方位角强制与其正交,得到B类线段新的平均方位角;然后调整每条线段,以线段中心点为轴心,将线段调整至新平均方位角,并求出新线段两两相交的交点作为新的端点;最后将所有新的端点依次首尾相连,得到一个规则化的建筑物外轮廓线(图2右图).
2.2 屋顶面内轮廓线提取
2.2.1 屋顶面聚类
要实现屋顶面内轮廓线提取,首先需要将复杂的屋顶面进行分割聚类,其中,具有代表性的聚类算法有:
1)区域增长法,该方法首先计算三角面片的局部特征(如法向量),然后根据面片的连通性和局部特征之间的关系来进行聚类,该算法过于简单,易受局部干扰点的影响;
2)空间Hough变换[20],该方法通过在参数空间里进行聚类的计算,因此需要对参数空间进行离散化,但离散化的程度会直接影响聚类的精度;
3)RANSAC算法[21],采用迭代的方式从一组包含离群的被观测数据中估算出数学模型的参数,该算法可以容忍数据集中含有的噪声,但它的聚类结果完美贴近数学意义上的一致性,忽略了数据携带的几何特性,因此不适合直接用于复杂建筑的基元提取.
本文提出了一种改进的RANSAC算法,先通过区域增长法粗分割屋顶面,充分挖掘数据中的几何信息,然后利用粗分割的结果作为先验知识,采用RANSAC算法从粗到细提取屋顶面.
(1)
建筑物屋顶通常是由多个平面或相对规则的曲面构成的,落在同一屋顶面上的三角面片法向量大致相同,因此,法向量是屋顶面粗聚类的重要特征.首先,随机定位区域增长的种子点,根据当前三角面片法向量和连通性判断,使用基于广度优先遍历的方法先将周围最近一圈的三角面片聚为一类,然后不同往外扩张,直至没有新的面片加入为止.使用RANSAC算法的基本思想是通过迭代随机的从样本集S中抽取一个样本子集S′,计算当前平面模型M,再从S中抽取符合平面模型M阈值条件的样本子集T,重复以上流程若干次,最后将迭代过程中得到的最大样本子集T作为最佳子集T*.但该算法存在一个缺陷,如式(1)所示该算法以一定的概率α得到一个满意的聚类结果.其中,ε为实际模型的概率,必须加大其迭代次数N,才能提高概率α.当遇到复杂数据时,算法的效率将会显著降低.
针对这个缺陷,本文设计一种基于先验知识的RANSAC算法提取屋顶面,将粗提取的聚类结果作为样本集S,利用局部采样方法获取样本子集S′.在α一定的情况下,减少了迭代次数.本系统中迭代次数N设为50,如图1的屋顶面内轮廓线提取部分的左图所示,可保证建筑物屋顶大部分平面聚类出来,且聚类时间在可接受范围内.实验部分将给出迭代次数的效果比较和具体的效率数据.
2.2.2 内轮廓线提取
内轮廓线主要是指两屋顶面相交的部分,可分为直交线段和悬交线段,直交线段是指直接相邻的两屋顶平面所构成的线段,悬交线段是指非直接相邻的两屋顶面向下投影到水平面后,互相紧邻且不存在重叠部分,但在两水平面上直接形成了一条明显的交界线.所以,内轮廓线都在相邻屋顶面之间产生,准确的找到屋顶面之间的邻接关系有助于提取出正确的内轮廓线.
本小节首先简要介绍一下获取屋顶面之间邻接关系的操作方法,详细步骤说明:首先将所有屋顶面上的点云投影到一个水平面,对该平面上的二维点云进行网格化处理,网格单元长度为平均点间距的2倍;然后对每个网格单元进行标记,统计每个网格单元内包含点云数量最多的屋顶面,将该屋顶面ID号作为该网格单元的标识;最后通过遍历每个网格单元,判断该单元八邻域内网格单元的标识符.若两个标识符不同,则这两个标识符所对应的两个屋顶面应为相邻屋顶面.
(2)
(3)
得到相邻屋顶面集合后,则可以计算两个屋顶面之间的内轮廓线.如前所述,内轮廓线段有两类:直交线段和悬交线段.其中,直交线段可以通过两平面的平面方程直接求交获取;悬交线段的计算更为复杂:首先通过将两平面先投影到一个水平面上,求出水平的候选悬交线段;然后求出该候选悬交线段所在的竖直平面方程;最后将竖直平面方程分别与两个屋顶平面方程求交,用求直交线段的方法分别求出两条悬交线段(图1的屋顶面内轮廓线提取部分的右图).直线方程可由式(2)的参数方程表示,其中,(a3,b3,c3)代表直线的方向向量,(x0,y0,z0)代表直线上任意一点.直线上任意一点可以取两个聚类的公共端点,或其中一个聚类的边缘点.直线的方向向量N3可以通过式(3)计算得到,其中,N1和N2是两平面的法向量.
2.3 规则化重构
2.3.1 平面基元的生成
平面基元是由线段顺序组合而成的闭合区域,平面基元的提取就是要确定每个闭合区域的轮廓,而轮廓是由外轮廓线段和内轮廓线段(直交线段和悬交线段)组成,但上述工作得到的线段端点通常不够精确,不能直接用于基元的提取.因此,需要对特征线段进行精化,具体是指根据建筑的几何特征修改线段的端点坐标,使线段端点满足相同端点坐标重合的条件,同时避免线段“虚相交”和“过相交”.
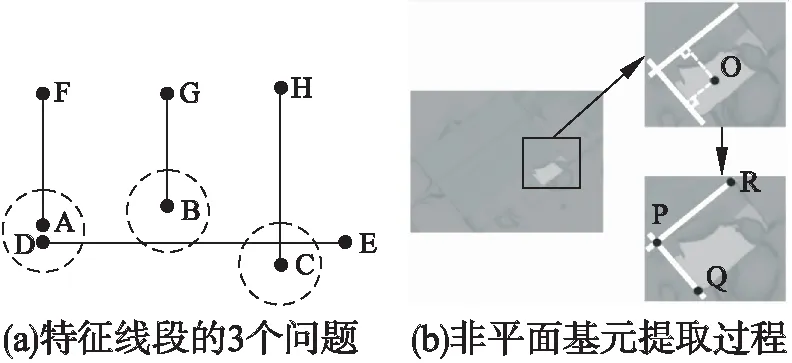
图3 规则化重构示意图Fig.3 Illustration of our regularized reconstruction
如图3(a),针对“顶点重合”、“虚相交”和“过相交”这3个问题分别进行一些形式化的定义,以便于对其进行统一处理.其中,将“顶点重合”问题定义为重合约束,是指两个顶点之间的距离小于一定的阈值;而将“虚相交”和“过相交”这两个问题定义为共线约束,是指某顶点到一特征线段的距离小于一定的阈值.如图3(a),AF、BG、CH和DE为待处理的特征线段,其中两个顶点A和D具有等式重合约束,应直接满足式(4)(其中xA、yA为顶点A的x坐标和y坐标,以此类推);顶点B落在DE直线上,具有共线约束,应满足式(5);同理,顶点C也具有共线约束,应满足式(5).本文通过将特征线段精化问题抽象成等式约束问题来求解,校正完每条特征线段后,按照先前的聚类结果将同一个平面上的特征线段依次按序相连,获得平面基元(图1的规则化模型的生成部分的左图).
(4)
(xB-xD)(yE-yD)-(xE-xD)(yB-yD)=0
(5)
2.3.2 非平面基元的生成
通过恢复所有平面基元每个顶点的高程值,并依序连接构成重构模型的屋顶面;然后将每个屋顶面顶点向地面投影,生成地面顶点,连接相应的屋顶面顶点和地面顶点构成几何多边形,作为模型的墙面,类似竖直往下挤压,生成平面基元的规则化重构结果,但该结果相对于原始模型是不完整的,缺少了因烟囱、太阳能等不规则物体而未被聚类的部分.因此需要将非平面基元部分重构出来.非平面基元由于其形状不是一个规则的平面,大多是凹凸不平的,所以不能放在屋顶面聚类过程中一起处理提取.本文在提取完屋顶面全部的平面基元后,对剩下的屋顶三角面片仅采用区域增长法,不考虑三角面片法向量之间的关系,进行非平面部分的连通性聚类,找出非平面基元的聚类后,本文将此部分进行平面化处理.如图3(b)左图,具体是先通过阈值设定,将大面积的非平面基元的聚类结果进行保留;然后如图3(b)右上图所示通过计算当前非平面聚类的中心点O,从中心点O出发找距离最近的两条轮廓线段,且这两条线段法向量互相垂直;最后如图3(b)右下图所示求出这两条轮廓线的交点P作为该非平面基元的一个顶点,以该顶点为起始点,向两边进行完整性探测,求出另外两个端点Q和R,最后再恢复出对角线上的顶点,将此非平面基元重构成矩形.
通过恢复所有平面和非平面基元每个顶点的高程值,得到具有三维坐标信息的空间平面.为了获得封闭的建筑物实体模型,先将每个基元上的顶点依序连接构成屋顶面,然后将每个屋顶面顶点向地面投影,生成地面顶点,并连接相应的屋顶面顶点和地面顶点构成几何多边形,作为重构模型的墙面,如图1右图所示,往下挤压生成最终的规则化模型.
3 实验结果与分析
本文方法已经在2.50 GHz Intel(R)Core(TM)PC机上的Microsoft Visual studio 2017平台利用C++实现.使用Windows平台下的OpenGL库和Qt库实现基于屋顶面轮廓线提取的规则化模型的重构.其中,利用OpenGL渲染三维建筑物模型,使用Qt进行用户界面的开发.根据输入的单幢建筑物的面片数据,自动进行高效的建筑物模型规则化重构,重构过程中,用户无需具备专业知识与技能,只需进行简单的参数调整,得到最优的规则化模型即可.
在考虑改进型RANSAC聚类算法迭代次数选取时,针对输入的三维建筑物,分别给出不同的迭代次数本文方法的聚类效果如图4所示.表1所示为对于不同迭代次数所需的聚类时间,可以看出,迭代次数N取50次时,聚类时间较快,且结果更精确.因此,本实验中所有模型在聚类时迭代次数N设定为50.
图5所示为本文方法与PolyFit方法的效果比较,针对单幢三维建筑物,PolyFit方法首先通过改进过的RANSAC聚类方法进行点云的聚类,然后用聚类出的结果将模型切割成小块的平面,再规则化提取出的平面,最后将问题转化为二进制标记问题,选出适合的候选平面,从而拟合出规则化重构模型.由于PolyFit方法对模型精度要求较高,本文分别将输入模型的点云进行采样至10万个、20万个和30万个,然后用PolyFit方法进行化简.图5(b)、(c)为点云采样至10万个和20万个的结果,可以看出PolyFit方法虽然可以快速简化出结果,但其过于追求模型的密闭性和整体性,模型中的一些局部特性(如边之间的平行性)不能很好的保留下来;而增加采样个数至30万个,由于聚类出的平面个数过多,PolyFit方法在二进制标记求解过程中陷入了复杂的计算中,无法输出最后的规则化重构结果.相对而言,本文方法能够规则化重构出更为精确的三维模型,且无需手动交互,大大减少了简化时间,提高了算法的效率.

图4 不同迭代次数下的聚类结果Fig.4 Clustering results with different iterations

表1 不同迭代次数下聚类时间统计Table1 Clustering time statistics under different iterations
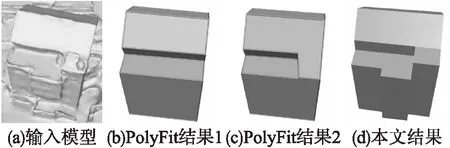
图5 本文与PolyFit方法比较Fig.5 Comparison between our method and PolyFit
值得指出的是,本文方法在场景中的规则化重构结果如图6(b)、(d)所示,能较好地实现绝大部分建筑物的规则化重构.图6(e)为场景中若干实例的规则化重构结果,其中,第1行为输入的原始三维建筑物模型,第2行表示最后的规则化重构模型.从图6(e)中可以看出,对于具有3个、5个和6个等不同屋顶面个数的建筑物,本文方法均能实现高效的模型规则化重构.与已有规则化重构方法比较,本文方法针对屋

图6 更多建筑规则化重构结果Fig.6 More results
顶由多边形组合成的建筑物在简化过程中交互简单,且能高效地实现贴近原始三维模型的简化效果.此外,对于非平面组成的构件(如太阳能、烟囱等),本文方法可以有效利用基元之间的相邻关系将非平面基元恢复成平面基元并完成规则化重构.然而,文方法难以处理由圆柱体、圆锥体、球体等部件组成的屋顶,未来将进一步考虑,使建筑物规则化重构方法适用性更广、实用性更强.
4 结 语
本文针对倾斜摄影技术重建的三维建筑模型,提出了一种基于屋顶轮廓线的三维建筑模型规则化重构方法,能够将复杂的、带噪声的三维建筑网格模型重构简化为简单、规则的建筑模型,首先分割屋顶并提取屋顶的外轮廓线,并对粗糙的外轮廓线进行精化;接着通过改进的平面拟合提取屋顶的内轮廓线;最后组合内外轮廓线,利用重合约束和共线约束进行优化生成平面基元;针对屋顶面中的非平面部分,本文通过连通性聚类进行规则化保留.本文方法不依赖用户交互和先验信息,实验结果表明了,本文方法在精确性和鲁棒性两个方面的优势.
然而,本文方法仅适用于屋顶由多边形组合而成的三维建筑物模型,对于其他更为复杂的建筑物(如屋顶由圆柱体、球体等构成的建筑物),则是未来需要进一步考虑的.另一方面,本文方法并没有考虑门、窗和阳台等细节的规则化.由于倾斜摄影技术重建的三维建筑模型精度并不高,直接对这些细节进行规则化的精度较差,将来可以利用深度学习技术对它们进行识别后再处理,或许能实现细粒度的三维建筑模型规则化重构.

