群智感知任务分配中的用户类型转换问题研究

黄丹镭，黄 河，，孙玉娥，陆 乐，吴晓灿，杜 扬

1(苏州大学 计算机科学与技术学院，江苏 苏州 215006) 2(苏州大学 轨道交通学院，江苏 苏州 215137) 3(中国科学技术大学 苏州研究院，江苏 苏州 215123)

1 引 言

群智感知技术利用配置在智能移动终端上的各类传感器(如加速度计、GPS、陀螺仪、相机等)，随时随地收集物理世界中感兴趣的数据，并进一步分析形成应用为我们的日常生活以及商业活动提供有效的服务与支持.作为一种新兴的大规模数据收集系统，群智感知系统大幅降低了数据收集所需的时间与成本、提高数据的采集规模，从而更容易通过分析得到大量的可信数据，进而为系统用户提供优质的服务.

智能移动终端用户完成数据采集任务需要付出相应的成本开销，例如电能损耗、网络流量损耗等，并会对设备的使用产生一定的影响.因此，大多数群智感知系统所能吸引到的用户数量是有限的，且不同的用户完成任务的质量是不同的.为了尽可能通过有限的用户收集到更多高可靠性的数据，需要设计合理的任务分配和激励机制，保证参与任务的用户均能高质量地完成任务.针对这一问题，已有大量研究提出了一系列高效的群智感知任务分配机制.例如，部分文献设计的任务分配机制将每个感知任务分配给多个用户完成，以保证任务能到得到高质量的感知数据[1-4].然而用户完成数据采集任务会花费一定的成本，因此群智感知系统需要对每个参与任务的用户支付一定的报酬.上述文献并未考虑用户完成质量之间的差异，而每个任务分配的用户越多，所需要支付的报酬也越多.为了减少群智感知系统的成本，应该尽可能地将任务分配给高质量的用户完成，而不是简单地分配给多个人完成.因此，在考虑用户可靠性的基础上，一些研究者设计了一系列高效的群智感知任务分配机制，以尽可能地将任务分配给高质量的用户完成[5-11].在上述研究的基础上，现有的一些研究还将用户的报酬与任务的实际完成质量相结合，以激励用户更好地完成任务[12，13].然而，在群智感知中用户完成任务的质量不光受到主观意愿(例如：做事的认真程度)的影响，还受到当前所处的状态、环境以及所持有的智能终端设备等客观因素的影响.对于任务完成质量不受主观意愿决定的用户来说，给予奖励或其他激励方式也无法使其变成高质量用户；反之，如果用户所提交的数据质量是由主观因素决定的，则可以通过给予额外的奖励来激励用户更好地参与任务.据我们的调研发现，现在还没有机制研究在任务分配之前，通过设置额外奖励的方式，激励低质量用户转换为高质量用户，从而利用有限的奖励最大化地提高任务的整体完成质量.

为了解决现有研究的不足，本文设计了一种群智感知用户类型转换方法，以实现任务间完成质量的最大最小公平为优化目标，研究在任务分配过程中如何分配有限的奖励给低质量用户，才能促使提交低质量感知数据的用户转变成为提交高质量感知数据的用户，从提高所收集数据的质量.首先，所设计的机制对用户进行分类，并拟合低质量用户的任务完成质量提升与奖励之间的关系曲线.然后，设计了一种最优任务及奖励分配机制，在每轮任务分配时决定将任务和奖励分配给哪些用户以及为每个分到任务的低质量用户分配多少奖励，从而最大化任务的最低完成质量.最后，通过仿真实验对所设计的机制性能进行了验证.

2 问题建模

本章首先给出所研究的群智感知系统模型，并对所研究用户类型转换问题给出形式化的描述.

2.1 系统模型

本文所研究的群智感知系统由一个任务发布者、一个群智感知平台和若干移动终端用户(后面简称用户)组成.用U={1，2，…，m}来表示用户集合，T={t1，t2，…，tn}来表示任务发布者发布的任务集合.所研究的群智感知系统的任务分配分周期进行.如图1所示，每个任务周期开始时首先由任务发布者将需要完成的任务发布在群智感知平台上.每个发布的群智感知任务包含一个任务描述，包含任务对用户技能以及感知设备性能等方面的要求.除此之外，每个任务还包含一个任务报价bj，即当用户完成任务后的实际支付.在本文所研究的模型中bj是一个固定值，不管将该任务分配给哪个用户完成所支付的除奖励之外的金额均等于bj.本文所研究的群智感知任务是异质的，即不同任务对用户的要求不同.在这里，我们将要求类似的任务认为是同一类任务，并将群智感知系统中的所有任务划分为e种不同的类型.我们用Tk来表示所有属于第k类的任务集合，且tj∈Tk.除此之外，参与群智感知任务的用户也是异质的.由于用户自身的技能、所持设备等方面的不同，不同用户完成同一任务的质量是不同的，即使是同一用户完成不同类型任务的质量也是不同的.用qi，k表示用户i完成类型为k的任务的期望完成质量.

图1 基于用户分类的最优奖励任务分配模型Fig.1 Structure of the allocation and reward system with user classification in crowdsensing system

每个用户在阅读任务描述之后，会向群智感知平台提交一组感兴趣的任务集合.然后，群智感知平台根据一定的规则将每个任务分配给一个用户完成.除此之外，每个用户在一个分配周期最多参与一个任务的完成.在实际的群智感知系统中，并不是每一个任务都能找到高质量的用户.在这种情况下，本文为候选用户集合中仅有低质量用户的任务提供一定的奖励，以激励这些任务的候选低质量用户更好地完成任务，进而转换为高质量用户，从而达到提高整体任务完成质量的目标.当用户完成任务后，群智感知平台还会评估每个用户在本轮的实际任务完成质量，并据此计算低质量用户的实际奖励金额完成支付.

2.2 问题描述

本文的设计目标是要使任务整体完成质量最大化.为了实现这一点，我们希望将任务分配给完成质量尽可能高的用户.如果用户i对任务tj感兴趣，那么就称用户i是任务tj的候选用户.但是，部分任务可能不存在高质量的候选用户.在这种情况下，就需要设计合理的激励机制，使得这些任务的候选低质量用户更加认真的完成任务，进而转换为高质量用户.任务发布者的总奖励金额预算用B来表示.群智感知平台分配给所有用户的总奖励金额应该不超过预算B.

用yi，j={0，1}表示用户i是否为任务tj的候选用户，其中yi，j=1表示用户i是任务tj的候选用户，而yi，j=0则表示用户i不是任务tj的候选用户.用xi，j={0，1}表示任务tj是否被分配给了用户i，其中xi，j=1表示群智感知平台将任务tj分配给了用户i；否则，xi，j=0.任务tj的完成质量用Qj表示，而任务完成质量的划分阈值用Th表示.若Qj≥Th，那我们称任务tj被高质量地完成；否则，称任务tj被低质量地完成.同样，若用户i完成任务tj的质量小于Th，则称用户i是任务tj的低质量用户；反之，用户i是任务tj的高质量用户.为了激励低质量用户更好地完成任务，群智感知平台会给部分用户分配额外的奖励.用ri来表示群智感知平台给用户i分配的奖励.对于分配了任务的低质量用户，若该用户最终高质量地完成了任务，即提交的感知数据的质量超过阈值Th，那么群智感知平台会在收到数据后支付额外的奖励ri；反之，若该用户并未提交高质量的感知数据，那么群智感知平台并不会向该用户支付奖励.本文的设计目标是要实现任务间完成质量的最大最小公平，也就是说要在满足约束的前提下使得max minQj.

3 基于用户类型转换的最优任务及奖励分配机制

为了最大化地提高所有任务的最低完成质量，基于用户类型转换的最优任务及奖励分配机制主要需要解决的问题是如何在感知任务分配过程中计算为哪些用户提供额外的奖励，以及奖励的金额是多少的问题.而要解决上述问题，我们首先需要对用户进行分类，找到每类任务的高质量用户和低质量用户.对于每一类任务，我们还需要构建出用户任务完成质量提升与奖励之间的关系曲线，为最优任务及奖励分配提供依据.因此，所设计的基于用户类型转换的最优任务及奖励分配机制包括两部分：用户任务完成质量提升与奖励关系曲线拟合以及最优任务及奖励分配.

3.1 用户任务完成质量提升与奖励关系拟合

不同类型的任务对设备和用户专业知识的要求不同，因此同一用户对不同任务所提交数据的质量可能也是不同的.群智感知平台在每次任务分配之前会首先按照采集数据的属性对任务进行分类，且在用户完成任务后会更新其所完成类型任务的期望完成质量.对于给定的阈值Th，若qi，k≥Th，则称用户i是类型为k的任务的高质量用户；否则，用户i是类型为k的任务的低质量用户.当发现一个用户为低质量用户时，需要首先拟合用户的历史任务完成质量提升与奖励之间的关系曲线，为接下来的奖励分配提供依据.需要说明的是，本文主要研究的是如何通过奖励机制促使用户提交高质量的感知数据，而根据收集到的数据估计出任务的真值并不在本文的研究范围之内.用Trj表示任务tj的真值，di，j表示用户i所提交的感知数据与真值之间的偏差.在这里，我们假设Trj是已知的，可以直接根据已有研究成果得到，例如：有的研究者通过使用最大期望算法(EM)对众包工人的质量进行了估计[14-16].Li等人[17]研究了一种增量真值发现框架，该框架可以在新数据到达时动态更新对象真值和源权重.一些研究则使用了贝叶斯方法来发现真值[18-22].根据任务的真值Trj和di，j偏差，可以进一步得到本轮用户i的任务完成质量为：

(1)

假设任务tj所属的类型为k.群智感知平台利用q′i，j可以进一步计算得到更新后的用户i完成类型为k的任务的期望完成质量：

qi，k=αq′i，k+(1-α)q′i，j

(2)

其中α是一个常数，满足0<α<1，并且q′i，k为上一个周期用户i完成类型为k的任务的期望完成质量.

(3)

pi，k表示为单位奖励所能带来的类型为k的任务的平均期望任务完成质量提升，由公式(4)求得：

(4)

我们可以进一步地得到任务完成质量提升值Δqi，k与奖励金额ri，k之间拟合后的关系式H(Δqi，k).据此可以求得任务完成质量提升值pi，k：

(5)

对于每个低质量用户，取最近l个提交低质量数据的周期的奖励与实际数据质量提升信息，将实际数据质量提升与奖励间关系用最小二乘法拟合为一条二次曲线；若该用户提交低质量数据的周期小于l，则取所有提交低质量数据的周期来拟合实际数据质量提升与奖励之间的关系曲线.因为同一用户在不同类型任务上的完成质量是不同的，所以需要为用户提交低质量数据的任务分类并分别拟合实际数据质量提升与奖励之间的关系曲线.用最小二乘法利用用户i最近l次数据进行二次曲线拟合的步骤如下：

1)构建向量

本文对数据进行二次曲线拟合，假设每个用户i在任务类型为k有l个历史记录，即有l个只有一个特征的样本.表示为(Δqi，k(1)，ri，k(1))，(Δqi，k(2)，ri，k(2))，…，(Δqi，k(l)，ri，k(l)).

首先，我们所构建的拟合函数由公式(6)所示：

HΘ(Δqi，k)=θ0+θ1Δqi，k+θ2Δqi，k2

(6)

其次，所构建的拟合函数的矩阵表达形式如公式(7)所示：

=ΘTΔQi，k

(7)

最后构建了3个向量.一个1×l的向量HΘ(Δqi，k)，一个3×1的参数向量Θ，以及一个3×l的向量ΔQi，k.

2)目标函数

为了选取的最合适的参数向量Θ，定义误差函数如公式(8)所示：

J(Θ)=(ΘTΔQi，k-Ri，k)T(ΘTΔQi，k-Ri，k)

(8)

求得拟合函数的关键是使得J(Θ)最小，并求出J(Θ)最小时拟合函数Θ的参数向量.

3)优化方法

将所定义的误差函数进行求解，误差函数展开如公式(9)：

=(ΘTΔQi，k-Ri，k)T(ΘTΔQi，k-Ri，k)

=ΘΔQi，kTΔQi，kΘT-2ΘΔQi，kTRi，k-Ri，kTRi，k

(9)

J(Θ)是关于Θ的二次函数，并且非负，因此存在最小值.最小化J(Θ)等价于梯度为零：

=-2ΔQi，kTRi，k+2ΔQi，kTΔQi，kΘT=0

(10)

最后求解：

ΔQi，kTΔQi，kΘT=ΔQi，kTRi，k

(11)

ΘT=(ΔQi，kTΔQi，k)-1ΔQi，kTRi，k

(12)

根据公式(12)可求得最终解，并可得到所需要的二次拟合曲线.

(13)

(14)

其中Uk为参与过类型任务为k的任务的用户集合且这些用户完成该类任务的次数大于f，用户集合中的用户数量为m′.

(15)

3.2 群智感知最优任务及奖励分配机制

假设群智感知系统对任务的总奖励预算为B.具体的任务及奖励分配流程如算法1所示.为了激励用户更好地完成任务并保证任务的完成质量，任务应该分配给期望完成质量最高的用户.因此，算法1首先遍历所有的任务以及每个任务的候选用户集合，找到期望任务完成质量最高的用户.当遍历到类型为k的任务tj时，若期望任务完成质量最高的用户i是高质量用户，即qi，k≥Th，那么直接将任务tj分配给用户i，并将用户i从其他任务的候选用户集中删除；否则，开始处理下一个任务.

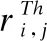
算法1.预算充足下的任务与奖励分配算法

输入：未分配任务集合T，总奖励预算B

输出：分配向量与奖励集合

1.while(T≠φ){

2.设置rTh=B；

3. for(每一个任务tj∈T)

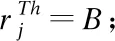
5. for(tj的每个候选用户i)

9. end if

10. end for

13. end if

14. end for

15. 将任务t′分配给需要奖励最少的候选用户，并将该候选用户从所有其他未分配任务的候选用户集合中删除；

17. 将任务t′从未分配任务集合T中删除；

18.}end while

然而，群智感知平台给出的总预算并不总能保证所有任务均可以被高质量地完成.当算法1计算得到的所有任务需要的奖励金额之和大于预算B时，则需要根据算法2来实现任务与奖励的最优分配.本文的优化目标是要实现任务完成质量之间的最大最小公平，也就是说要使min{Qj}tj∈T达到最大.为了实现这一目标，我们采用二分法来计算得到给定预算B下的min{Qj}tj∈T最大值.对于这种情况，具体的任务和奖励分配方法如算法2所示.

算法2.预算不足下的最优任务及奖励分配算法

输入：未分配任务集合T，总奖励预算B

输出：分配向量与奖励集合

1.设置Thmin=Th，qmax=Th，qmin=min{qj}tj∈T；

2.Flag=1

3.while TRUE {

5. ifFlag=1

7. return；

8. else

9.Flag=0；

11. end if

13. return；

16. else

18. end if

19.}end while

令qj表示任务tj在不设置奖励时的候选用户的最大期望任务完成质量.在此Thmin表示奖励预算受限时所有任务的期望完成质量的下界，即Thmin=min{Qj}tj∈T，那么很容易得到奖励预算不足时Thmin满足min{qj}tj∈T≤Thmin

4 实验分析

对于本文所提出的用户分类以及任务匹配两个阶段，本章将构造一个模拟实验模型，并以此来分析和验证所研究的机制的性能.

4.1 任务数量与申请用户数对任务期望完成质量下界的影响

图2 任务数量与任务期望完成质量下界之间的关系Fig.2 Relationship between number of tasks and task expected completion quality

4.2 奖励预算与实际奖励之间的关系

图3 奖励预算与实际奖励之间的关系图Fig.3 Reward budget and actual reward comparison chart

图3(a)以及图3(b)显示了在阈值分别为ThB=2，ThB=0.8时，奖励预算金额与实际奖励金额之间的关系.我们设置阈值ThB的目的是使得实际奖励金额尽可能地靠近奖励预算B，以确保任务的完成质量尽可能高.可以看到与阈值ThB=2时相比，在阈值ThB=0.8的情况下，实际的奖励金额会更接近奖励预算.因此，在相同的奖励预算限制下，其任务期望完成质量下界Thmin也更高.

4.3 高质量用户以及低质量用户划分结果

图4是根据高质量用户和低质量用户的完成类型为k的任务期望完成质量和平均获得的奖励来表示他们的分布.我们通过公式(2)对用户在该类任务中的期望完成质量qi，k进行计算，并与阈值Th进行比较.将qi，k≥Th的用户划分为高质量用户，qi，k

图4 高质量用户以及低质量用户划分结果Fig.4 Result of user category division

4.4 低质量用户划分结果

表1 低质量用户划分结果Table 1 Result of low-quality user category division

将我们的划分法与标准划分方法相比较可以看到，在参与任务的低质量用户数量相同时，我们的划分方法划分出的不可转换低质量用户数量远大于标准方法划分出的不可转换的低质量用户数量.同时，当期望完成质量相同时，我们的划分方法总的奖励金额、可转换的低质量用户平均所获得的奖励金额以及不可转换用户平均所获得的奖励金额均低于标准划分方法对应的各项奖励金额.因此，实验证实了我们所用的划分方法更能有效的划分低质量用户的类型.

5 总 结

本文研究了基于激励机制的用户分类任务分配问题.为了促进将低质用户转变为高质量用户，本文首先提出一种用户类型转换机制，以便在任务分配过程中尽可能将任务分配给具有较高历史完成质量的用户.通过合理的激励机制，促进了低质量群智感知用户的转化.此外，提出了一种最优任务及奖励分配算法，以最大化任务的最低完成质量为优化目标，保证了所有任务间完成质量的最大最小公平，使得在预算有限的情况下最大化任务完成的质量.最后，通过仿真验证了所提机制的有效性.