HPM视野下函数概念的教学思考

崔恩华 刘爱琴

摘  要：根据历史发生原理，从学生的角度选取数学史上几个关键的函数概念，研究它们定义的缘由，以及它们之间的联系，从本源上对高中函数概念和学生的困惑进行深入探讨，从而分析出学生困惑的原因，并给出函数概念生成的教学建议和思路，帮助学生解决困惑，真正理解函数的本质.

关键词：函数;变量;对应;集合

一、引言

函数是中学数学的核心概念，函数概念形成的过程是曲折且漫长的，是数学家认识不断深化的智慧结晶，更体现了一种数学精神. 数学是研究现实中数量关系和空间形式的科学，而函数研究的是两个变量之间的数量关系，主要价值在于找出数量规律，从而揭示和把握事物之间的运动变化规律. 然而，没有数量规律的对应关系为什么也是函数呢？函数为什么是单值对应而不是多值对应？高中函数为什么要建立在集合上，与初中函数有什么区别？这些问题始终困扰着很多学生，仅仅研究初中和高中教材中函数概念的区别与联系，或者只是罗列数学史上不同时期的函数定义无法解决学生的困惑. 基于学生在数学学习中的思维过程及困惑与数学史上数学家的思维过程及困惑具有相似性，根据HPM中的历史发生原理，本文从学生的角度选取数学史上关于函数的几个关键定义，深入研究其定义的缘由及定义之间的联系，从而分析出学生困惑的原因，并以此为依据设计出函数概念生成的教学思路，使学生真正理解函数的概念.

二、函数概念的本源性分析

1. 什么是对应

函数起源于科学的数学化，伽利略主张用实验和数学的方法去研究自然规律，他在研究静止物体自由落体运动时，通过实验获得时间[t]和对应下落距离[s]的两组数据，两组数据中每对[s]和[t]的数据都服从同一个规律，即[s=kt2，] 进而揭示出自由落体定律，这也是研究函数的主要价值和初衷. 函数就是研究两个变量之间的数量关系，这种关系通常用解析式表示. 欧拉在《无穷小分析引论》中给出函数的定义：变量的函数就是变量和常量用某种方式联合在一起的解析式. 这种解析式也包括无穷项的级数，另外，函数又分为单值函数和多值函数. 在学习高中函数概念时，学生通常无法准确说出初中函数的定义，但是能熟练地举出函数的例子. 例如，一次函数、反比例函数、二次函数等. 然而，从未举出甚至不愿接纳没有解析式的图象和表格所表示的函数，这些都说明了学生对函数概念的认知起点是解析式，从函数研究的主要价值和学生学习函数的经验来说，学生更愿意接受函数是解析式.

当两个变量对应的两组数据之间没有规律时，无法用解析式表示，预示着两个变量之间可能没有依赖关系，那么，此时这两个变量之间的数量关系是不是函数呢？因为研究两个无关的变量是件毫无意义的事情，而且没有解析式的函数是无法研究的，所以当时的数学家称它为假函数. 另外，一个解析式被称为一个函数，所以分段函数被看成多个函数，这在当时都是很自然的事情. 欧拉研究弦振动时也遇到了类似的问题，因为初始弦的形状是任意的，欧拉意识到应该改变函数的定义，于是他在《微分学原理》中给出函数的另一个定义：如果某些变量，以这样一种方式依赖于另一些变量，即当后者变化时，前者也随之变化，则称前面的变量就是后面变量的函数. 欧拉提到“在[xy]平面上随手画一条曲线就是表示[y]与[x]的函数关系”. 虽然欧拉改变函数定义的做法是对的，但是没有说服力，因为当时普遍认为函数就是解析式，如果把随手画的一条曲线能用一个解析式表达出来，那么可以承认它是函数，但是当时对任意形状的初始弦能否用三角级数表示存在争议. 以往高中函数概念的教学通常给出解析式、图象、表格这三种问题情境，采取概念形成的方式，即从同类事物的不同例证中抽象出共同的关键属性，然而这三种情境在学生眼里并不是同类事物，因为解析式作为关键属性把数量关系分成有无规律的两类，这也是学生不愿承认没有解析式的对应关系是函数的原因. 只要把随手画的一条曲线能用一个解析式表达出来，学生自然愿意接受它是函数，所以此处适合采取概念同化的教学方式，而解析式就是概念同化的固着点.

如果函数是一种对应，那么傅里叶展开式是不是对于任意函数都成立呢？答案是否定的，狄利克雷给出了它成立的一个充分条件，并给出反例：狄利克雷函数[Dx=1，当x为有理数，0，当x为无理数.] 狄利克雷函数是无法用解析式表示的，它也没有傅里叶展开式，它验证了函数的本质是一种对应而不是解析式. 狄利克雷给出了现在常用的函数定义：如果对于给定区间上的每一个[x]的值有唯一的一个[y]的值同它对应，那么[y]就是[x]的一个函数.

因此，初中和高中的函数定义本质上是相同的，不同的是初中的函数定义是变量对应说，高中的函数定义是集合对应说，高中函数定义更严谨些. 高中函数概念的教学通常给出解析式、图象、表格这三种问题情境，然后提问学生这三种情境中所对应的关系是否为函数，再引导学生利用集合对应的方式来体会函数是对应的本质. 然而，初中函数的学习并没有使学生突破变量之间依赖关系的束缚，学生只能用初中函数定义中“每一个[x]对应唯一的一个[y]”的表面意思去判定函数，缺少从突破变量依赖关系的角度去经历“对应”的生成过程，所以学生很难真正理解函数的本质，自然也无法接受没有解析式的图象和表格所对应的关系是函数.

2. 函数为什么是单值对应

3. 函数为什么建立在集合上

三、函数概念生成的教学思路

综合以上分析，确定函数概念生成的主要教学思路是：解析式—变量对应—集合对应，具体过程如下.

问题1：（情境1）伽利略在研究静止物体自由落体运动时，通过实验获得的时间[t]和对应下落距离[s]的数据如表1所示.

试问：时间[t]和对应下落距離[s]之间有什么数量关系吗？它是函数吗？

【设计意图】探索两组数据之间的数量关系是函数的根源，让学生体会函数的主要价值，培养学生的数据分析和数学抽象素养，把学生的认知起点——解析式作为函数概念同化的固着点.

问题2：如图1，在平面直角坐标系[xOy]中随手画的一条曲线，它存在表达式吗？它是函数吗？

【设计意图】把任意曲线与学生熟悉的解析式之间建立实质性的联系，通过讲解数学史的方式打破变量之间数量规律的分类标准，转变函数是解析式的错误观念，同时突破函数是变量之间的依赖关系的束缚，让学生体会函数的本质是对应，感受数学家的智慧和数学文化.

问题3：若函数是一种单值对应，那么是不是所有的单值对应都有解析式呢？

【设计意图】让学生意识到解析式不等价于单值对应，体会函数的本质是单值对应而不是解析式，感受数学文化和科学精神.

问题4：试判断下列两个情境中的对应关系是不是函数？

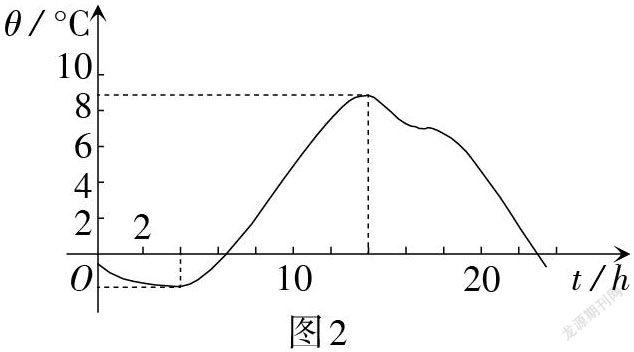
（1）（情境2）某市一天24小时内的气温变化图如图2所示.

（2）（情境3）我国1949—1999年人口数据如表2所示.

【设计意图】从多个角度揭示函数概念的内涵，让学生体会函数的本质是单值对应.

可以让学生画出函数的图象，通过图象看出这两个函数是不同的，尽管两个函数的表达式相同，即对应方式相同，但是[x]的取值范围不同，导致这两个函数不同，所以有必要说明[x]的取值范围. 用什么来表示范围呢？显然，集合是最合适的，所以我们要把函数定义在集合上.

【设计意图】让学生体会函数建立在集合上的必要性和数学的严谨.

问题6：把情境1 ～ 情境3中两个变量的范围用集合表示出来，它们的对应方式分别是什么？

问题7：你能用集合与对应的语言来刻画函数的概念吗？

【设计意图】培养学生的概括能力和数学语言表达能力.

四、结束语

函数概念的教学应该关注学生已有的认知结构和概念发展过程中的逻辑关系，应该体现函数的内涵和外延在实际需要和数学发展中不断变化的过程. 本文的目的不是对函数概念数学史的完整再现和罗列，而是从教学的角度去理解数学史，再从数学史的角度去分析教学，重点做到数学史与学生认知的完美结合，让学生经历概念产生和发展的过程，有助于学生更好地掌握概念的内涵和外延，体会其中的数学思想和科学精神.

参考文献：

[1]莫里斯·克莱因. 古今数学思想[M]. 张理京，张锦炎，江泽涵，等译. 上海：上海科学技术出版社，2002.

[2]欧拉. 无穷小分析引论（上）[M]. 张廷伦，译. 哈尔滨：哈尔滨工业大学出版社，2013.

[3]林仁炳. HPM视角下微积分思想方法溯源[M]. 上海：上海交通大学出版社，2015.

[4]傅里叶. 热的解析理论[M]. 桂质亮，译，北京：北京大学出版社，2008.

[5]曹才翰，章建跃. 数学教育心理学[M]. 北京：北京师范大學出版社，2006.

[6]贾随军. 傅里叶级数理论的起源[D]. 西安：西北大学，2010.

3314501908274