单接收机时间差分实时位移计算及分析*
周 适,段太生,王靠省,杨维裕,郭 平,晏 勇,干坚定
1.中铁二局集团有限公司,四川 成都 610031
2.中铁二局第五工程有限公司,四川 成都 610091
目前,动态测量技术在工程上应用较广泛的是常规RTK 技术和网络RTK 技术。常规RTK 技术工作范围一般为10 ~15km,若超出工作范围,定位精度无法达到厘米级[1]。流动站离基准站越近,定位精度越高。根据工程实际经验,观测条件较好的地区时整周模糊度能得到正确的双差固定解,定位精度能达到1cm 甚至几毫米,一般情形下定位精度在2cm 以下[2]。常规RTK 技术采用单基站模式,数据采用电台超高频UHF 传输RTCM 差分信号,常规RTK 技术将定位作业范围限制在离基准站周围较小的区域,因此假设流动站和基准站相对电离层延迟较小是合理的[3],一旦流动站和基准站距离超过一定范围,则无法满足厘米级的定位精度。
网络RTK 技术又称多基准站RTK 定位技术,目前最常用的是虚拟参考站技术(VRS),此外还包括区域改正数技术(FKP)和主辅站技术(MAX)。网络RTK 技术由于采用多基准站同时作业,当一个连续运行基准站(CORS)出现故障时,仍然可以通过其他正常的参考站进行定位,因此提高了系统的可靠性。
与常规RTK 技术相比,扩大了作业范围,定位精度分布均匀,精度能达到厘米级。常规RTK 技术在一定的工作范围内定位精度和网络RTK 技术不相上下,但随着流动站与基准站距离不断增大,常规RTK 技术无法达到网络RTK技术的定位精度。未来在中国大部分区域,网络RTK 技术将取代常规RTK 技术进行动态定位测量。网络RTK 技术在中国地区正在飞速发展,部分区域CORS 站布设密度和相关技术能力已经能满足区域厘米级定位精度要求。若继续提高覆盖范围,需要布设更多的CORS 站,这增加了系统复杂性和维护成本。
文章采用单接收机时间差分原理进行动态定位,处理方法简单,不需要架设基站和接收精密星历(接收广播星历即可),只需使用一台GNSS 接收机,不需要通信设备,定位精度能达到厘米级,但该方法也存在一定局限性,如测试数据稳定性不足,平面定位精度在2cm 以下的维持时间较短,还需进行深入研究,但从技术创新角度来看,这是一种简易动态定位方法。下面首先简要介绍单接收机时间差分定位的数学模型,并通过C#编程实现,再利用实测数据进行测试和分析。
1 单接收机时间差分定位的数学模型(GPS 单系统)
将GNSS 接收机架设在A 点上,文章采用的数学模型以GPS 卫星信号为例,BDS 可同理写出。在时刻t1,对参考卫星r 发送L1频率卫星信号,可列出线性化后的观测方程[4]:


同理,对于其他卫星s,可列出观测方程:
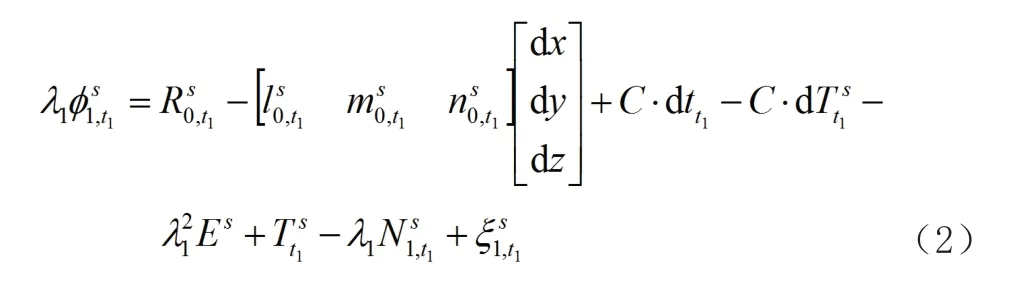
对于1 个历元接收到的n 颗GPS 卫星,除了参考卫星r,其他卫星数量为n-1,式(2)可列出n-1 个方程。将其他卫星s 和参考卫星r 进行星间单差[5],即用式(2)减去式(1),此时可消去C·dtt1,,即消去接收机钟差影响项可得到如下方程:

组合不同频率的观测值,采用无电离层模型,由于GPS的L1频率值为1575.42MHz,L2频率值为1227.60MHz,可写出GPS 两个频率的波长比值:

同理,从A 点移动到B 点,时刻从t1变化为t2,可列出式(7):


式(11)中,为求权阵P,可根据误差传播定律对方差阵D 进行推导,将式(8)中方程左边观测值展开后,可得式(12):

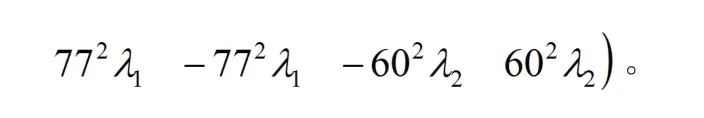
先赋值参考卫星r 的系数,再赋值其他卫星s 的系数,由于星间单差每个观测方程都是其他卫星和参考卫星作差,设历元t1时刻到t2时刻的GPS 公共卫星数量为n,除了参考卫星r,其他卫星数量为n-1。可列出n-1 个观测方程,系数矩阵K 的行数为n-1,列数为4n,第1 ~4 列为参考卫星r 的系数,第5 ~8 列为其他卫星中第1 颗卫星的系数,依次类推,矩阵第n-1 行最后4 列是第n-1 颗卫星的系数。系数矩阵K 可表示为式(13):
对比GPS 两个不同频率的波长比值,将式(6)~式(14)中的77 替换成763,60 替换成590,即得到单独BDS 系统下时间差分计算位移基线向量的数学模型。
若采用BDS 和GPS 混合卫星系统,则星间单差计算方式有两种[9]:一种是采用GPS 和BDS 各选择系统内的一个参考卫星,分开组合星间单差;另一种是仅选择一个参考卫星,组混合单差。考虑到组混合单差需要引入系统间偏差,算法较为复杂,文章采用第一种计算方式,即BDS 和GPS 分别各选择系统内的一颗卫星作为参考卫星,按照上述

设载波相位观测值方差阵为Dφ,载波相位观测值精度可近似为波长的1/100,考虑不同卫星的高度角不同,高度角越高的卫星权值越大,方差越小[7],不同频率、不同时刻的载波相位值是独立不相关的[8],载波相位观测值方差阵Dφ行数和列数均为4n,矩阵主对角线上每4 个值为1 组,首先是参考卫星r 的载波相位观测值方差(L1频率t2时刻、L1频率t1时刻、L2频率t2时刻、L2频率t1时刻),然后是其他卫星的载波相位观测值方差,从第1 颗卫星开始一直到第n-1 颗卫星,方差阵除了主对角线的元素有数值(非零),其余元素值为0(协方差为0 表示独立不相关),方差阵 Dφ的主对角线元素可表示为式(14):

以上为单接收机在GPS 单卫星系统下时间差分计算位移基线向量的数学模型。
2 单接收机时间差分位移基线向量的数学模型
前文已介绍GPS 单卫星系统下利用时间差分模型计算的位移基线向量,下面介绍BDS 单卫星系统和GPS、BDS 混合卫星系统下该数学模型的使用方法。文章采用的是双频无电离层模型,BDS 的B1和B2频率值分别为1561.098MHz、1207.140MHz,写出BDS 两个频率的波长比:公式进行计算。

设历元t1时刻到t2时刻,历元间接收机能接收到的公共卫星信息,有n 颗北斗卫星,m 颗GPS 卫星的观测数据,可写出组合卫星系统的误差方程式:

3 实测数据计算及精度分析
笔者按照上述单接收机时间差分计算位移基线向量的数学模型,利用C#语言进行编程。为测试该方法的定位精度,特选择一组静态数据,由于静态数据没有位移,时间差分计算的位移值基线向量理论上应该为0,这样便于比较各历元计算的结果。测试数据采用北方地区某控制点外业静态数据,采样间隔为10s,高度截止角为15°。这里只对前30min 的数据计算结果进行数据分析,根据其他若干大量数据计算证实,该方法达到平面厘米级精度(平面定位误差在10cm 以下)持续的时间一般小于30min,30min 后计算的结果精度不能满足厘米级的精度要求。展示采用GPS 单卫星系统,BDS 单卫星系统,GPS、BDS 混合卫星系统计算的位移基线向量结果,并进行比较分析。

图1 单接收机外业操作流程图
计算得到的位移基线向量是空间直角坐标系下的(ΔX,ΔY,ΔZ),为便于直观显示平面和高程方向的位移数值,将其转换为站心坐标系下的位移基线向量(ΔN,ΔE,ΔU)[10],即计算北、东、天各方向上的位移数值。单独GPS 卫星系统下计算得到的N、E、U 方向的位移基线向量各分量数值见图2 ~图4;单独BDS 卫星系统下计算得到的N、E、U 方向的位移基线向量各分量数值见图5 ~图7;GPS、BDS 混合卫星系统下计算得到的N、E、U 方向的位移基线向量各分量数值见图8 ~图10。在图2 ~图10 中,横坐标为统计的历元数,第0 个历元为初始历元,测站坐标采用伪距单点定位计算的结果,未在图中展示,从第1 个历元到第183 个历元,历元间采样间隔为10s,均是与第0个历元进行时间差分计算后得出的位移基线向量结果。纵坐标为N、E、U 各方向上的位移分量值,单位为cm。
从图2 ~图10 中可看出,GPS、BDS 混合卫星系统计算结果整体稳定性略优于GPS 和BDS 单卫星系统。以第30min(采样间隔为10s,相当于第180 个历元)计算的位移基线向量值为例,GPS、BDS 混合卫星系统下:N 方向为3.43cm,E 方向为10.56cm,U 方向为24.12cm。

图2 GPS 单卫星系统下N 方向各历元时间差分位移分量值
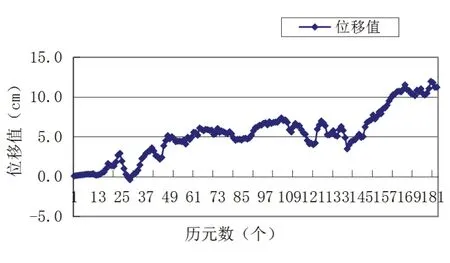
图3 GPS 单卫星系统下E 方向各历元时间差分位移分量值
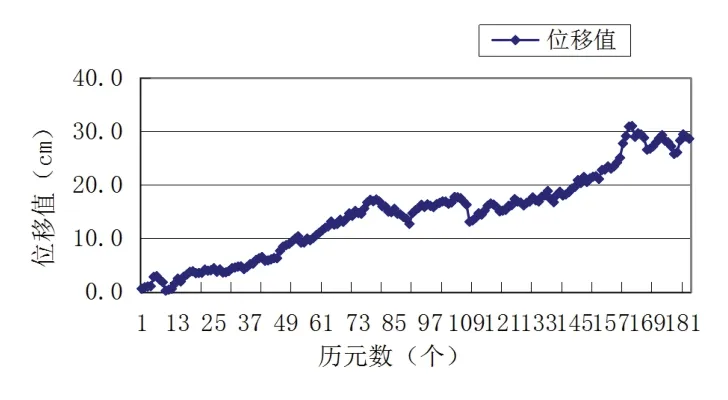
图4 GPS 单卫星系统下U 方向各历元时间差分位移分量值

图5 BDS 单卫星系统下N 方向各历元时间差分位移分量值

图6 BDS 单卫星系统下E 方向各历元时间差分位移分量值

图7 BDS 单卫星系统下U 方向各历元时间差分位移分量值

图8 GPS、BDS 混合卫星系统下N 方向各历元时间差分位移分量值
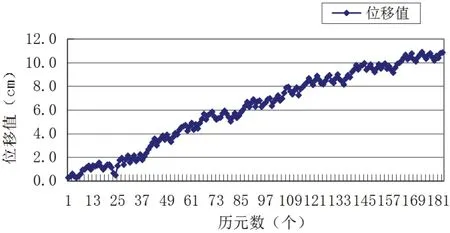
图9 GPS、BDS 混合卫星系统下E 方向各历元时间差分位移分量值
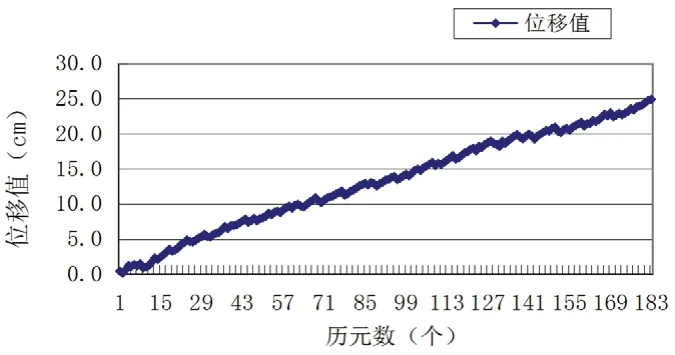
图10 GPS、BDS 混合卫星系统下U 方向各历元时间差分位移分量值
GPS 单卫星系统下:N 方向为2.69cm,E 方向为11.96cm,U 方向为28.31cm。BDS 单卫星系统下:N 方向为4.64cm,E方向为12.54cm,U 方向为29.74cm。根据数据可知,GPS、BDS 混合卫星系统下在第180 个历元时的计算位移值,在E、U 方向上比单卫星系统下小,只是N 方向计算位移值比GPS单系统略大,但比BDS 单卫星系统位移计算值小。相邻历元间的位移基线向量变化不大,平面N、E 方向向量变化均在1cm 以下。单接收机时间差分计算位移基线向量的精度随着时间推移逐渐下降,这是由于历元间误差的相关性逐渐减弱引起的[11]。其中,高程U 方向定位精度明显低于平面N、E 方向定位精度,且随着时间的推移,高程U 方向精度下降速率明显快于平面N、E 方向。若以平面厘米级精度(N、E 方向位移基线向量小于10cm)作为衡量指标,GPS 单卫星系统下,第161 个历元(第26.8min)E 方向位移计算值达到10.28cm,BDS 单卫星系统下,第146 个历元(第24.3min)E 方向位移计算值达到10.14cm,GPS、BDS混合卫星系统下,第163 个历元(第27.1min)E 方向位移计算值达到10.13cm。综合GPS 单卫星系统,BDS 单卫星系统,GPS、BDS 混合卫星系统三种情形下的计算结果,时间差分计算位移基线向量精度能达到平面厘米级的持续时间约25min,超出这个时间后,计算精度不能满足平面厘米级的精度要求,这主要是由于时空效应引起的。该计算模型依据传播路径上对流层、电离层延迟等误差在短时间内具有较强相关性和没有周跳发生时模糊度固定不变的特点,但随着时间的推移,对流层延迟等参数不再具有强相关性[12],接收机钟差、多路径效应也需要纳入误差模型考虑范围,因而直接利用历元间作差求解的数学模型就暴露出其缺陷。与常规RTK 技术进行对比,常规RTK 技术因为基准站始终有一台GNSS 接收机接收卫星观测值,可收集和分析对流层延迟等改正参数,利用基准站和流动站进行差分求解运算,因此可消除一定范围内强相关性的误差,且精度不会随着时间推移明显下降,除非发生卫星失锁或电台通信中断等情形。
文章采用的计算方法,虽然只采用一台接收机,不需要电台通信,但是移动过程中卫星不能失锁,且平面定位精度在厘米级的时间较短,随着时间的推移,精度逐渐越低。若以平面2cm 的精度作为衡量指标,则持续时间更短,单卫星系统下平面能达到2cm 精度的时长约3min,GPS、BDS混合卫星系统下平面能达到2cm 精度的时长也不到5min。一般而言,2cm 以下的定位测量精度对于实际工程测量才有利用价值,但该方法能达到2cm 精度维持的时间太短,该方法的实际利用价值还需要进一步的探讨和研究。该方法与网络RTK 技术对比,网络RTK 技术因为定位精度的稳定性、可靠性、大范围、长时间等显著特点,具有非常好的发展前景,是未来动态定位的趋势和发展方向。
4 结束语
文章对GPS、BDS 混合卫星系统下,单接收机时间差分计算位移基线向量的算法进行了详细介绍,并通过实测数据进行测试,得出了以下结论:(1)单接收机时间差分计算位移基线向量的精度随着时间推移逐渐下降,这是由于历元间误差的相关性逐渐减弱引起的,其中,高程U 方向精度低于平面N、E 方向的精度,且随着时间的推移,高程U 方向精度下降速率明显快于平面N、E 方向。(2)GPS、BDS 混合卫星系统下定位精度整体稳定性略优于GPS 和BDS单卫星系统的定位精度。若以平面厘米级精度(N、E 方向定位误差小于10cm)作为衡量指标,则采用文章方法能维持平面厘米级精度的时间在25min 内,超出一定的时间范围后,定位精度无法达到10cm。(3)单接收机时间差分模型进行动态定位的算法与常规RTK 技术和网络RTK 技术进行对比,由于文章模型无法解决定位精度会随着时间推移明显降低这一问题,因此还存在明显缺陷,需要进一步加强研究。网络RTK 技术在未来动态定位中具有可以预见的发展前景。

