幂零布尔矩阵及其积和式的图论属性*

韦扬江，邢 悦，张小凤，周美江，陶冰雨

(南宁师范大学 数学与统计学院，广西 南宁 530100)

1 引言

布尔矩阵是仅由0和1组成的矩阵，它在计算机网络、通信工程、逻辑学、图论、布尔网络等领域有着广泛的应用.很多学者对布尔矩阵进行了多方面的研究.早在1982年，Kim在[1]中就收集了大量关于布尔矩阵的研究成果.文献[2-5]从代数和图论的角度研究了幂等布尔矩阵，文献[6，7]研究了布尔矩阵的平方根.但目前关于幂零布尔矩阵的研究结果较少，文献[8，9]用代数方法对交换反环上的幂零矩阵进行了若干研究.

本文在文献[8]的基础上进一步研究幂零布尔矩阵：给出了布尔矩阵的积和式为1图论刻画；根据幂零布尔矩阵的图结构获得其伴随矩阵对应的有向图，进而构造伴随矩阵，并得到了幂零布尔矩阵的伴随矩阵的一些性质；对[8]中的两个相关结论，在布尔矩阵的情形给出了较为简单的证明.

2 相关定义

半环是一个代数系统(S,+, ·)，其中(S,+)是以0为单位元的交换幺半群，(S, ·)是以1为单位元的幺半群.如果在S中由a+b=0可推出a=b=0，则称S是一个反环(antiring).在集合B={0,1}上定义二元运算“+”和“·”如下：0+0=0，1+1=1+0=0+1=1，1·1=1，0·0=0·1=1·0=0.易见(B,+, ·)是一个反环，称为布尔半环,其上的一个m×n矩阵称为布尔矩阵，这样的m×n矩阵的集合用Mm×n(B)表示.简记Mn×n(B)为Mn(B).用Aij或aij表示矩阵A=(aij)的(i,j)-元.布尔矩阵的运算与一般数域上的矩阵的运算相同，其区别在于布尔矩阵中规定1+1=1.如果存在正整数k使得布尔矩阵A满足Ak=0，则称A是幂零的.

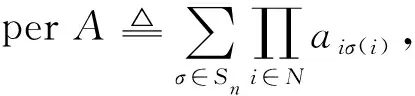
令S为反环，对于矩阵A=(aij)∈Mn(S)，定义有向图D(A)=(V,E),其中顶点集V={1,2,…,n}，边集E={(i,j)|aij≠0}.若ai0i1≠0，ai1i2≠0,…,aim-1im≠0，则称P:i0→i1→…→im是一条长度为m的路；如果i0=im，则称P是一个圈；进一步地，若i1,…,im互不相同,则称圈P是简单的.由[8]中的Proposition3.4知，布尔矩阵A是幂零的当且仅当D(A)是无圈图.

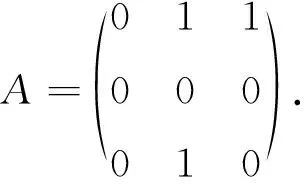
(1)perA=0×0×0+1×0×0+1×0×1+1×0×0+0×1×0+0×1×0=0.

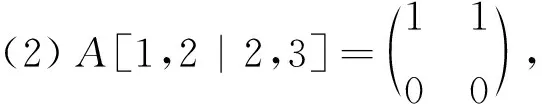
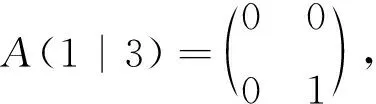
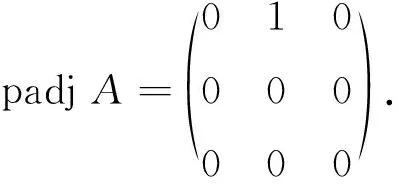
3 主要结果

定理3.1设A=(aij)∈Mn(B)，则perA=1当且仅当D(A)的n个顶点分别位于若干个不相交的简单圈.

从而有ai1i2…aik-1ikaiki1=1，…，aik+tik+t+1…ain-1inainik+t=1.因此在D(A)中存在圈

C1:i1→i2→…→ik→i1，…，Cm:ik+t→…→in→ik+t.

由于对任意p≠q都有ip≠iq，故C1,…,Cm为两两不相交的简单圈.

充分性.设D(A)的n个顶点分别位于m个不相交的简单圈

C1:i1→i2→…→ik→i1，…，Cm:ik+t→…→in→ik+t，

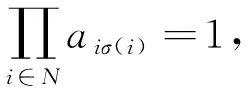
推论3.2设A∈Mn(B)，则perA=0当且仅当D(A)的n个顶点不分别位于若干个不相交的简单圈.

接下来讨论B上的幂零矩阵的性质.以下均设A=(aij)为B上的一个n阶幂零矩阵.

定理3.3A必有零行和零列.

证明若A没有零行，则它每行至少有一个1，不妨设ai0i1=ai1i2=ai2i3=…=ain-1in=1.由A幂零知D(A)是无圈图，因此顶点i0,i1,i2,…,in-1两两不同，从而存在0≤k≤n-1使得ik=in.于是D(A)中有圈

ik→ik+1→…→in-1→ik，

这便与D(A)无圈矛盾.同理可证A有零列.

推论3.4当A只有一个零行且只有一个零列时，padjA中只有一个元素为1，其余元素均为0；当A的零行数大于1或零列数大于1时，padjA为零矩阵.

证明(1) 设A只有第i行是零行，只有第j列是零列，则余子矩阵A(i|j)=(bm k)中每一行每一列都至少有一个元素为1.不妨令b1j1=b2j2=…=bn-1,jn-1=1,且j1,j2,…,jn-1两两不同.则b1j1b2j2…bn-1,jn-1=1. 因此(padjA)ji=perA(i|j)=1.当s≠j以及t≠i时，余子矩阵A(t|s)都存在零行或零列.故padjAst=perA(t|s)=0.

(2)A的零行(列)数大于1时，对任意i,j∈N，A(i|j)中都存在至少一个零行(列)，故perA(i|j)=0，因此padjA为零矩阵.

定理3.5(padjA)ij=1当且仅当在D(A)中存在从顶点i到顶点j的长度为n-1的路.

反之，设D(A)中存在从顶点i到顶点j的长度为n-1的路：i→l1→l2→…→ln-2→j,则ail1al1l2…aln-2j=1.由于D(A)为无圈图，故i,l1,…,ln-2,j两两不同.易知perA(j|i)=1，即(padjA)ij=1.

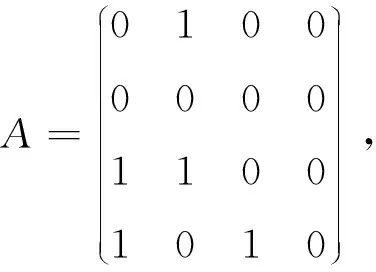
图1 有向图D(A)

文献[8]中的Theorem 3.2给出了关于反环S上的幂零矩阵A的两个结论：A·(padjA)=0和(padjA)2=0，其中S没有非0的幂零元，但证明方法较为繁杂.下面针对幂零布尔矩阵,从图的角度对以上两个结论给出较为简单的证明.

定理3.6A·(padjA)=(padjA)·A=0.

证明令C=A·(padjA).若存在i,j∈N使得Cij=1，则有

因此存在k∈N使得Aik·(padjA)kj=1，即得Aik=(padjA)k j=1.由(padjA)kj=1及定理3.5,D(A)中存在从k到j的长度为n-1的路P：k→…→j.由于D(A)无圈，故P的n个顶点两两不同，从而顶点i必在P上，又Aik=1，则D(A)中有圈k→…→i→k，矛盾.因此对任意i,j∈N都有Cij=0，即A·(padjA)=0.同理可证(padjA)·A=0.

定理3.7(padjA)2=0.

证明令C=(padjA)2.若有某个Cij=1，则存在k∈N使得(padjA)ik=(padjA)kj=1.由定理3.5知，D(A)中存在两条长度为n-1的路，即P1:i→…→k和P2:k→…→j.由于D(A)无圈，故P1的n个顶点两两不同，从而顶点j必在P1上，这导致D(A)中有圈j→…→k→…→j，矛盾.由此知C=0.