自激式水力振荡器的优化设计
赵 传 伟
中石化胜利石油工程有限公司钻井工艺研究院
0 引言
目前,开发页岩气在钻井技术方面仍面临着许多挑战,如长水平段水平井摩阻高、扭矩大,托压严重,轨迹难控制等。在北美页岩气水平井开发中,多采用旋转导向工具,有效地解决了上述问题[1-3]。由于国产旋转导向工具目前尚不成熟,为了控制成本多采用“优化井眼轨迹+常规导向动力钻具+水力振荡器”的方式[4]。水力振荡器产生的振动能将钻具与井壁间的静摩擦转变为动摩擦,降低摩阻,进而解决托压问题[5-7]。但现有水力振荡器普遍存在运动件和橡胶件,因而耐高温和腐蚀性能较差,且压耗较大、成本较高[8-10]。这些问题也制约了水力振荡器在页岩气水平井中的推广应用。为此,笔者基于附壁效应研制出了一种新型水力振荡器——自激式水力振荡器。该工具利用特殊流道和钻井液循环产生周期性振动,无运动件和橡胶件,耐高温、耐腐蚀、可靠性高、成本低。前期3 口井的现场试验表明,该工具能够有效解决滑动钻进托压问题,工具面更容易控制,同时显著提高了钻井效率。但是该工具压降较大、易导致泥浆泵过载,限制了其推广应用。因此,需要优化工具内部流道结构参数、降低工具压降。但在工具压降降低的同时,冲击力也会减小。如何合理地设计流道结构参数,在保证较大冲击力的同时降低压降,是该工具研制的难点之一。目前,与此相关的研究尚未见报道。为此,笔者提出采用Plackett-Burman 设计和Taguchi 方法相结合的方式来优化工具流道结构参数,并通过数值模拟和室内实验验证了所选优化方法的有效性。
1 结构及工作原理
自激式水力振荡器的结构示意图如图1 所示,主要包括上接头、下接头和流道体三部分。其中,流道体内部的流道结构主要由入口、射流流道、上分流流道、上反馈控制流道、第一旋流腔、第一出口、下分流流道、下反馈控制流道、第二旋流腔以及第二出口组成。工具适用于Ø215.9 mm 井眼。自激式水力振荡器的工作原理如图2 所示。
钻井液从上接头进入工具内部,由入口进入射流流道,形成高速射流;由于附壁效应,高速射流会偏向上分流流道(图2-a),进入第一旋流腔;一部分钻井液在第一旋流腔内形成顺时针方向的涡流(图2-a),并由第一出口流出,经下接头右端进入下部钻具内,另一部分钻井液进入第二旋流腔,形成逆时针方向的涡流(图2-a);进入该旋流腔的钻井液,一部分通过第二出口排出至下部钻具内,另一部分由上反馈控制流道到达射流流道的出口端;由于涡流场的外围压力高,中心压力低,工具进出口产生一定的压差;随着涡流场的强度逐渐增强,进出口压差不断变大;同时反馈调节作用也逐渐增强,迫使射流方向转换,钻井液开始由上分流流道进入下分流流道;由于下分流流道内液流的方向与第一旋流腔内涡流的方向相反,导致涡流场的强度开始降低,同时第二旋流腔内涡流场的强度也开始降低,直至第二旋流腔内涡流消失;然后,第一旋流腔内,一部分钻井液开始产生逆时针方向的涡流(图2-b),并由第一出口流入下部钻具内,另一部分钻井液进入第二旋流腔,形成顺时针方向的涡流(图2-b);进入第二旋流腔的钻井液,一部分通过第二出口排出至下部钻具内,另一部分由下反馈控制流道到达射流流道的出口端;随着涡流场强度的增强,进出口压差越来越大;同时反馈调节作用不断增强,迫使射流方向转换,即液流开始从下分流流道进入上分流流道;由于上分流流道内液流的方向与第一旋流腔内涡流方向相反,导致涡流强度开始降低,同时第二旋流腔内涡流场强度也开始降低,直至第二旋流腔内涡流消失;至此,完成一个工作周期。随着钻井液的不断循环,上述过程不断重复,工具产生周期性的振动。

图1 自激式水力振荡器及其内部流道图
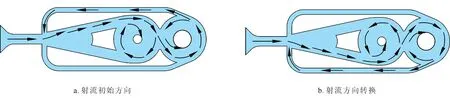
图2 自激式水力振荡器工作原理示意图
前期研究表明,流道体内部的流道深度一定的情况下,影响工具压降和冲击力的主要参数有射流流道宽度l1、入口与分流劈尖的距离l2、入口与第一旋流腔的距离l3、入口与第二旋流腔的距离l4、分流流道宽度l5、反馈控制流道宽度l6、旋流腔的直径d、分流流道倾角α、第一出口直径d1及第二出口直径d2,如图3 所示。通过单因素试验研究,初步确定10个参数的值分别为:l1=13 mm、l2=114 mm、l3=213 mm、l4=290 mm、l5=15 mm、l6=8 mm、d=76 mm、α=12°、d1=13 mm、d2=24 mm。室内模拟试验测得,排量30 L/s、清水条件下,工具压降为3.7 MPa,冲击力为44.5 kN(对应压降幅值4.1 MPa)。但现场应用时,由于钻井液密度普遍大于水的密度,工具压降通常大于4 MPa;而且随着井深增加,钻井液密度一般逐渐增大,工具压降亦逐渐增大,易导致泥浆泵过载。这使得工具应用范围受限。因此,需要优化工具内部流道结构参数,在保证较大冲击力的同时进一步降低工具压降。

图3 自激式水力振荡器主要流道参数示意图
2 优化设计方法
2.1 Plackett-Burman 设计方法
Plackett-Burman 设计对每个因子取两个水平进行分析,通过比较各因子两水平的差异与整体的差异来确定因子对响应影响的显著性[11-12]。该方法不能区分各因子间的交互作用,但能够以最少的实验次数有效地筛选出显著影响因子[13]。该方法与目前常用的部分因子实验相比,筛选显著因子效率更高[14]。因此,采用Plackett-Burman 设计方法筛选对工具压降和冲击力有显著影响的因子。
2.2 Taguchi 方法
Taguchi 方法是用正交表来设计实验并获得最佳的参数组合的局部优化方法[15-16]。遗传算法、模拟退火算法以及粒子群算法等全局优化算法,均需要建立目标函数,通过编程求解进行优化,过程较繁琐。而Taguchi 法不需要建立目标函数,利用较少的实验次数和数据,即可快速地搜索出最佳参数组合,并且可用于多目标优化[17]。因此,采用Taguchi 方法优化Plackett-Burman 设计方法从待优化因子中筛选出显著影响因子。其设计步骤如下[18-19]:①确定优化目标及待优化参数;②确定优待化参数的水平值;③选取合适正交实验表并建立正交实验表,安排实验;④根据正交实验表进行仿真实验,得到相应的仿真结果;⑤对实验数据进行分析、比较,确定最佳的参数组合。
2.3 数值计算方法
利用计算流体动力学软件进行流场数值仿真分析,用于计算下文Plackett-Burman 设计和正交实验设计中的响应值(工具压降和压降幅值)。采用六面体网格划分流体模型网格,经过网格无关性验证后得到的网格数量为183 253 个。计算湍流模型设定为RNG k-ε 模型[20],压力—速度耦合算法设定为SIMPLE 算法。仿真用流体介质为水,密度为1 000 kg/m3。入口边界条件设定为速度入口,入口流量30 L/s;出口边界条件设定为压力出口,出口压力为0 Pa;其余边界设定为壁面边界条件,按无滑移边界条件来处理[21-22]。
3 优化设计方法
3.1 Plackett-Burman 设计确定显著影响因子
在确定的流道参数基础上,为每个因子取2 个水平,即高水平(+1)和低水平(-1)。表1 所示为各因子的水平取值。待优化参数有10 个,因此选用实验次数为12的Plackett-Burman 设计表,实验安排及通过数值计算得到的响应值如表2 所示,Y1、Y2分别代表平均压降(MPa)、压降幅值Δp(MPa)。

表1 Plackett-Burman 设计的因子与水平设计表
利用t 检验确定因子的显著性[23],显著性水平取0.05,对应t=12.71。图4-a 为以平均压降为响应的标准化效应Pareto 图。可见,H、J 和C 对表现为正效应,A、G、I、D、F、B 和E 则表现为负效应。根据效应大小,这10 个因子对平均压降的影响顺序依次为A、G、I、H、D、J、F、B、C、E。其中,A、G、I 和H 的标准化效应值大于t=12.71,表现为显著。
图4-b 为以压降幅值Δp 为响应的标准化效应Pareto 图。H、D 和F 对Δp 表现为正效应,A、I、G、C、J、E 和B 则表现为负效应。根据效应大小,这10 个因子对压降幅值的影响顺序依次为:A、I、H、G、D、C、F、J、E、B。其中,A、I、H 和G 的标准化效应值大于t=12.71,表现为显著。
3.2 显著影响因子的优化
3.2.1 显著因子的水平取值及正交实验设计
东北航线经俄罗斯北部海域,由太平洋进入白令海峡,依次途经楚科奇海、东西伯利亚海、拉普捷夫海、喀拉海、巴伦支海至摩尔曼斯克港[8],因航线环境和破冰船的限制,目前适航船舶主要是阿芙拉船型。海冰是影响东北航线通航的重要因素。
根据Plackett-Burman 设计结果,以因子的初始参数为中心点,为3 个显著影响因子各取2 个水平,如表3 所示。待优化因子有4 个,每个因子取了3 个水平,因此选择L9(34)的正交表。正交实验安排及通过数值计算得到的响应值如表4 所示。其中,非显著因子保持初始值不变。
3.2.2 均值分析
均值分析能够确定出各因子的不同水平对响应影响的主次关系及最佳方案[24-25]。响应的平均值计算公式为:

式中K 表示响应的平均值;Yi表示第i 次实验的响应值;n 表示正交实验的次数。

表2 Plackett-Burman 设计实验安排及结果表

图4 不同响应的标准化效应Pareto 图
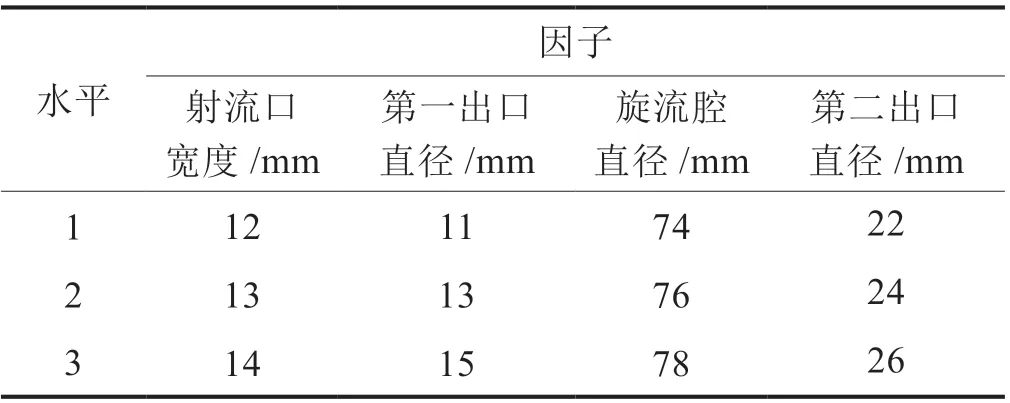
表3 因子水平取值表
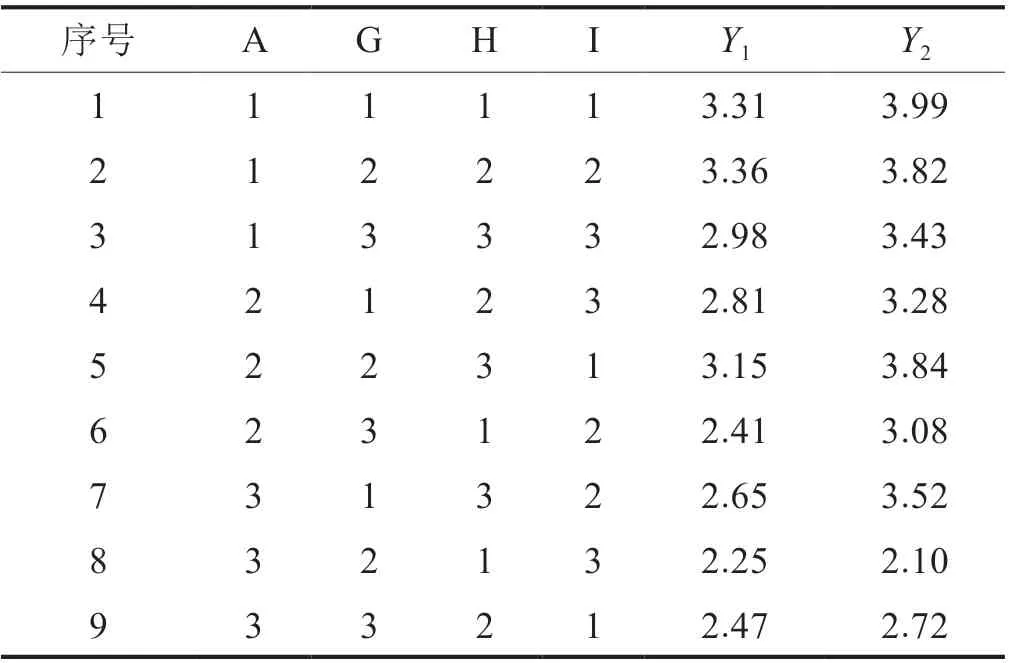
表4 正交实验设计及数值计算结果表
下面计算不同因子和水平对响应的平均值。例如,因子A 的水平1 对响应Y2的平均值,其计算式为:

同理,可得出所有因子各水平对响应Y1和Y2的平均值。对于同一个因子,其各水平对响应的平均值的最大值与最小值之差称为极差。不同水平对响应Y1和Y2的平均值及极差计算结果分别如表5、6 所示。
极差能够反映各因子对响应的重要程度[26]。水平对响应的平均值可以确定各因子的水平取值。根据表5,可以确定使平均压降为最小的组合是 [A3,G3,I3,H1]。由表6 可知,使压降幅值Δp 最大的组合是[A1,I1,H3,G1]。同时使得平均压降和压降幅值最优的组合不能直接确定。可通过方差分析评估因子对响应的影响比重,由此确定最优组合。

表5 不同水平对响应Y1 的平均值表

表6 不同水平对响应Y2 的平均值表
3.2.3 方差分析
方差计算公式为:

式中X 表示因子的代号A、G、H、I;Yj表示响应,j=1、2;KXi(Yj)表示因子X 的第i 个水平对响应Yj的平均值;K(Yj)表示响应Yj所有分析结果的平均值。各因子对响应Y1和Y2的方差,如表7 所示。
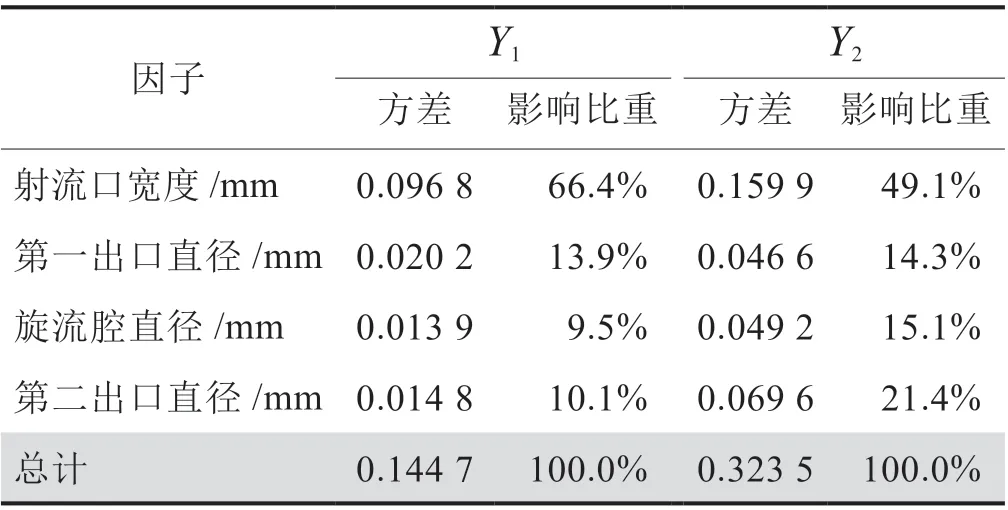
表7 不同因子对不同响应的方差及影响比重表
由表7 可知,射流口宽度对平均压降的影响要大于对压降幅值的影响,而第一出口直径、旋流腔直径、第二出口直径对平均压降的影响要小于对压降幅值的影响。根据保证压降幅值较大的同时降低工具压降的优化要求,可确定最优组合为[A3,G1,I1,H3]。 按照上述优化设计方法,最终确定最优参数组合为:射流口宽度14 mm,第一出口直径11 mm,第二出口直径22 mm,旋流腔直径78 mm。
4 优化前后工具性能对比
分别按照优化前、优化后的自激式水力振荡器的流道结构参数建模,并按照上述数值计算方法得到排量为30 L/s 条件下,工具的进出口压降随时间的变化曲线,如图5 所示,优化前,平均压降(波峰与波谷压力之和的一半)为3.6 MPa,压降幅值(波峰与波谷压力之差)为4 MPa;优化后,平均压降为2.9 MPa,压降幅值为3.5 MPa。

图5 自激式水力振荡器优化前后压降变化图
为了进一步评价优化后自激式水力振荡器的性能,进行了室内实验,实验流程及实物连接图如图6所示。主要试验设备及仪器包括:钻井泥浆泵、自激式水力振荡器、压力传感器、电磁流量传感器、水箱以及阀门V1、V2。水箱中装有清水,钻井泥浆泵将水箱中的清水泵送至水力振荡器的入口,清水经过水力振荡器后,回流至水箱内。电磁流量传感器和压力传感器位于泵的出口处。采集的流量及压力数据经过配套的数据处理软件处理后,显示在计算机终端。

图6 自激式水力振荡器室内实验流程图
实验测得的优化前后工具的平均压降和压降幅值,根据测得的压降幅值和工具内部过流面积可计算出工具产生的冲击力(表8)。由表8 可知,随着排量增大,工具压降及压降幅值均增大。优化后,不同排量条件下的平均压降和压降幅值均减小。其中,在设计排量30 L/s 条件下,优化后平均压降由3.7 MPa变为3.0 MPa,降低了18.9%;冲击力由44.5 kN 变为41.3 kN,降低了7.2%,达到了优化目标。因此,采用Plackett-Burman 设计和Taguchi 方法相结合的方式优化工具流道结构参数是有效的。

表8 自激式水力振荡器优化前后性能参数对比表
5 结论
1)射流口宽度、第一出口直径、旋流腔直径和第二出口直径对自激式水力振荡器的平均压降和压降幅值的具有重要影响。
2)旋流腔直径对平均压降和压降幅值表现为正效应,即减小旋流腔直径有利于降低平均压降,同时压降幅值也会减小。射流口宽度、第一出口直径和第二出口直径对平均压降和压降幅值表现为负效应,即增大射流口宽度、第一出口直径或第二出口直径有利于降低平均压降,同时压降幅值也会减小。
3)室内实验结果均表明,采用Plackett-Burman设计和Taguchi 方法相结合的方式优化工具流道结构参数是可行的。

