考虑孔径分布的页岩吸附气含量计算模型

赵 军 邓佳杰 杨 林 刘 凯 黄 科 何羽飞

1.西南石油大学地球科学与技术学院 2.中国石油集团测井有限公司油气评价中心

0 引言

准确评估含气性对于页岩气储层评价来说是一项十分关键的工作，对页岩气勘探开发具有重要的意义[1-6]。通常页岩气在储层中主要以吸附态和游离态2 种赋存状态存在，已有的研究成果表明，孔隙较大的微米孔隙及裂缝中主要以游离态气体为主，有机质及固体表面主要以吸附气为主[6]。作为页岩气的重要组成部分的吸附气占页岩气总量的20%～85%。因此页岩气的开发很大程度上都取决于对页岩吸附气量的评价[7-9]。研究发现，页岩气体是以超临界状态存在于地下高温高压环境中的[10]。兰格缪尔（Langmuir）等温吸附实验结果往往表现为在高压段的吸附气量随压力増加而减小，使用典型的Langmuir 等温吸附模型的拟合效果往往很差[11-14]。为了解决上述问题，目前大多数国内外学者都采用吸附相密度修正等温吸附模型。但吸附相密度不能直接通过实验测取，第一种做法认为超临界态类似于气体液化，吸附相密度直接等于0.423 g/cm3[15-16]；第二种做法则利用实验数据线性化拟合过剩吸附量下降段来求取吸附相密度[17-20]。此外，吸附相密度还可以通过实验数据非线性回归求取[21-22]。但上述方法目前都存在着一定的局限性：首先，在地层条件下吸附密度是随地层温压条件而变化的且变化范围较大，通常介于0.163 ～0.424 g/cm3[23]；此外，通过实验数据拟合得到的吸附相密度也存在着大于0.424 g/cm3的情况[20]。

为了提高页岩吸附气含量计算的精度，笔者基于经典分子动力学理论和方法，首先对有机质在不同孔径大小下的甲烷吸附相密度进行模拟研究，分析不同条件下甲烷吸附相密度随孔径大小的分布规律，建立吸附相密度随孔径的经验关系；然后根据页岩孔径分布的特点，建立基于吸附相密度修正的Langmuir 等温吸附模型，使用该方法对实际资料进行了处理，发现在实际储层压力下绝对与过剩吸附气量之差超过2 倍。对比分析的结果表明，采用修正模型计算的结果与实测数据吻合度更好。

1 分子动力学模拟

分子动力学以牛顿运动方程为基础，以多分子、原子体系为其主要模拟对象，通常各个分子的势能与动能组成了系统的总能量，组成分子的各个原子可通过函数式来表达系统的总势能，一般由范德华作用势能和内势能两部分组成，即

式中U 表示系统总势能，J；UVDW表示范德华作用力势能，J；Uin表示内势能，J。

范德华力作用计算公式为：

式中uij表示分子i 与分子j 之间的范德华力，N；rij表示分子i 与分子j 之间的距离，m。

原子i 所受的力（Fi）为：

式中Fi表示原子i 受到的作用力，N；xi表示原子i在x 坐标上求偏导；yi表示原子i 在y 坐标上求偏导；zi表示原子i 在z 坐标上求偏导。

原子i 的加速度ai为：

式中ai表示原子i 的加速度，N/kg；mi表示原子i 的质量，kg。

原子i 经过时间t 后的速度（vi）与位置（ri）为：

式中vi表示原子i 经过时间t 后的速度，m/s；vi0表示t=0 时原子i 的速度，m/s；ri表示原子i 经过时间t 后位置，m；t 表示原子i 所经过的时间，s；ri0表示t=0 时原子i 的位置，m。

根据上述原理，分子动力学的基本模拟步骤如图1 所示[24-25]。

2 模型建立

由于干酪根具有复杂的结构与分子构成，难以准确地还原干酪根的分子构型。因此在模拟有机质模型时主要采用单壁碳纳米管、石墨烯狭缝，或者根据数据自主构建干酪根孔隙模型[26]。本文利用石墨烯构建的层间结构来代替有机质的层间结构，利用石墨烯片层缝模拟有机质纳米孔，使用的晶格参数如表1 所示。然后将甲烷构型导入建好的有机质模型中，进行后续的吸附模拟。最终所构建的有机质模型如图2 所示。

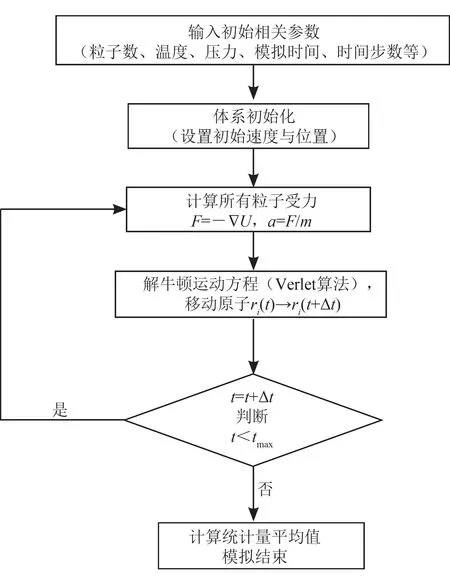
图1 分子动力学模拟方法流程图

3 吸附相密度计算

利用分子动力学模拟算法对石墨烯系统进行最小化能量设置，通过改变原子空间结构位置得到最初的稳固形态。在此基础上，利用巨正则模拟算法计算充填在有机孔中的吸附相分子数量，然后利用蒙特卡洛法判别优先吸附位。

模拟结束后将充填孔隙中的吸附相分子模型导出，通过分子坐标，计算分子类型和数量，进而计算超临界气体的密度值（ρ）。计算公式为：

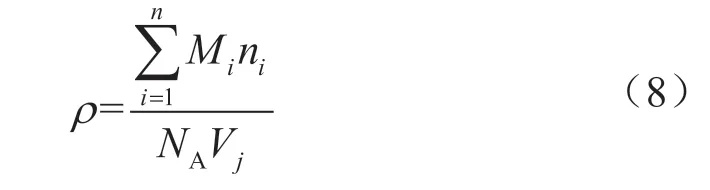
式中i 表示分子种类；Mi表示i 分子的相对分子质量，无量纲；ni表示小盒子内含有的i 分子数量，个；NA表示阿伏伽德罗常数，mol-1；Vj表示第j 个小盒子的体积，m3。

在模型结构参数、温度及压力不变的情况下，模拟计算得到的不同孔径下的吸附相密度值如表2 所示。

表1 石墨烯晶格参数表

图2 石墨烯结构透视效果图

表2 不同孔径大小的吸附相密度表

3.1 温度对吸附相密度的影响

为了研究温度对吸附相密度的影响，分别模拟了5 组不同温度（280 K、340 K、370 K、400 K、460 K）条件下的吸附相密度，其模拟结果如图3 所示。

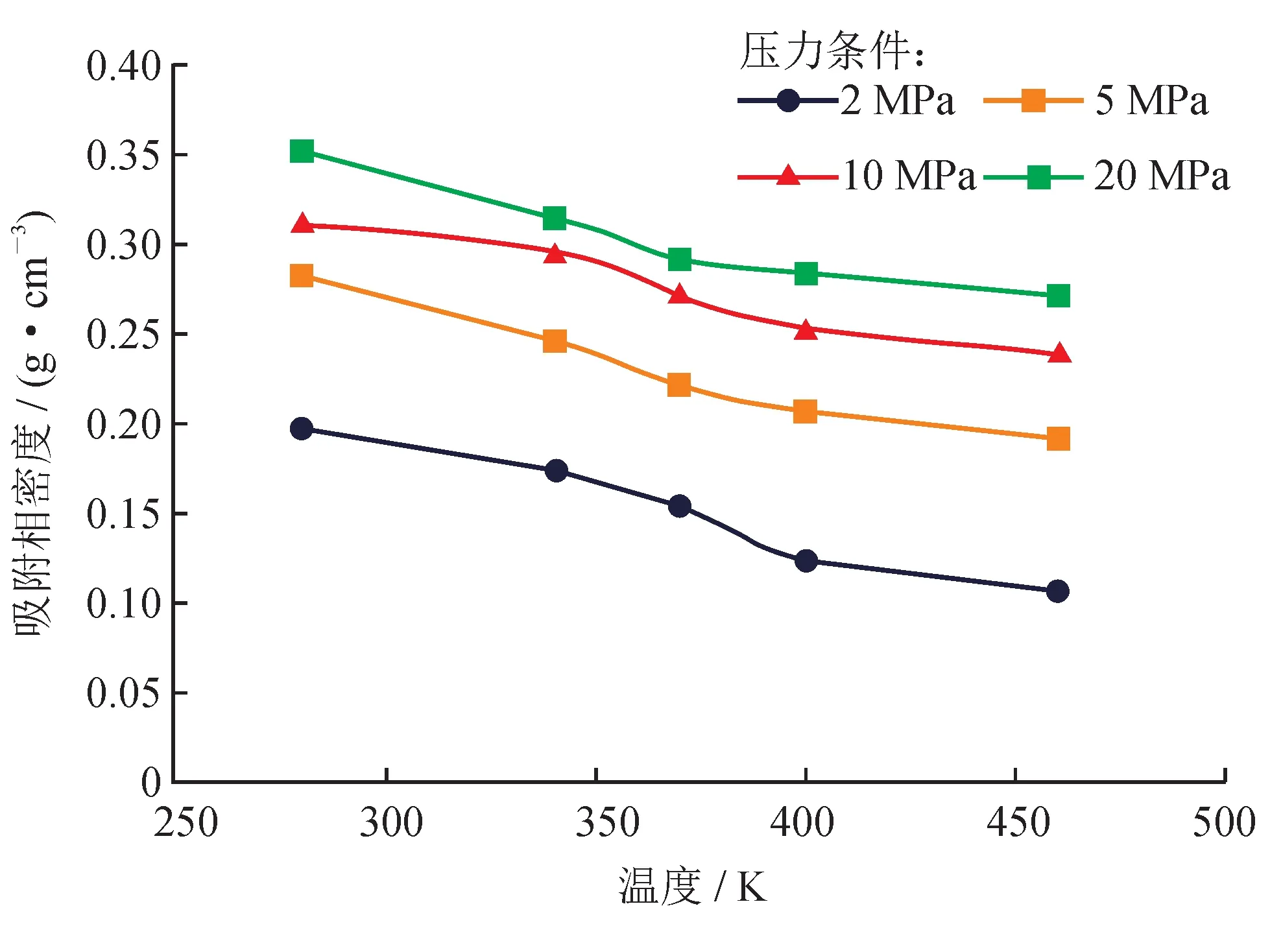
图3 温度与吸附相密度关系图

模拟结果表明，在不同压力条件下，吸附相密度均随着温度的增加而减小。在其他条件一致时，随着温度的增加，甲烷分子能够从外界得到更多的能量，因而也越容易脱离岩石表面的吸附。因此温度越高，吸附相密度也就越小，且随着温度的继续增加，吸附相密度的减小逐渐趋缓。

3.2 压力对吸附相密度的影响

分别模拟了9 组不同压力（0 MPa、2 MPa、5 MPa、10 MPa、20 MPa、30 MPa、40 MPa、50 MPa、60 MPa）条件下的吸附相密度，模拟结果如图4 所示。

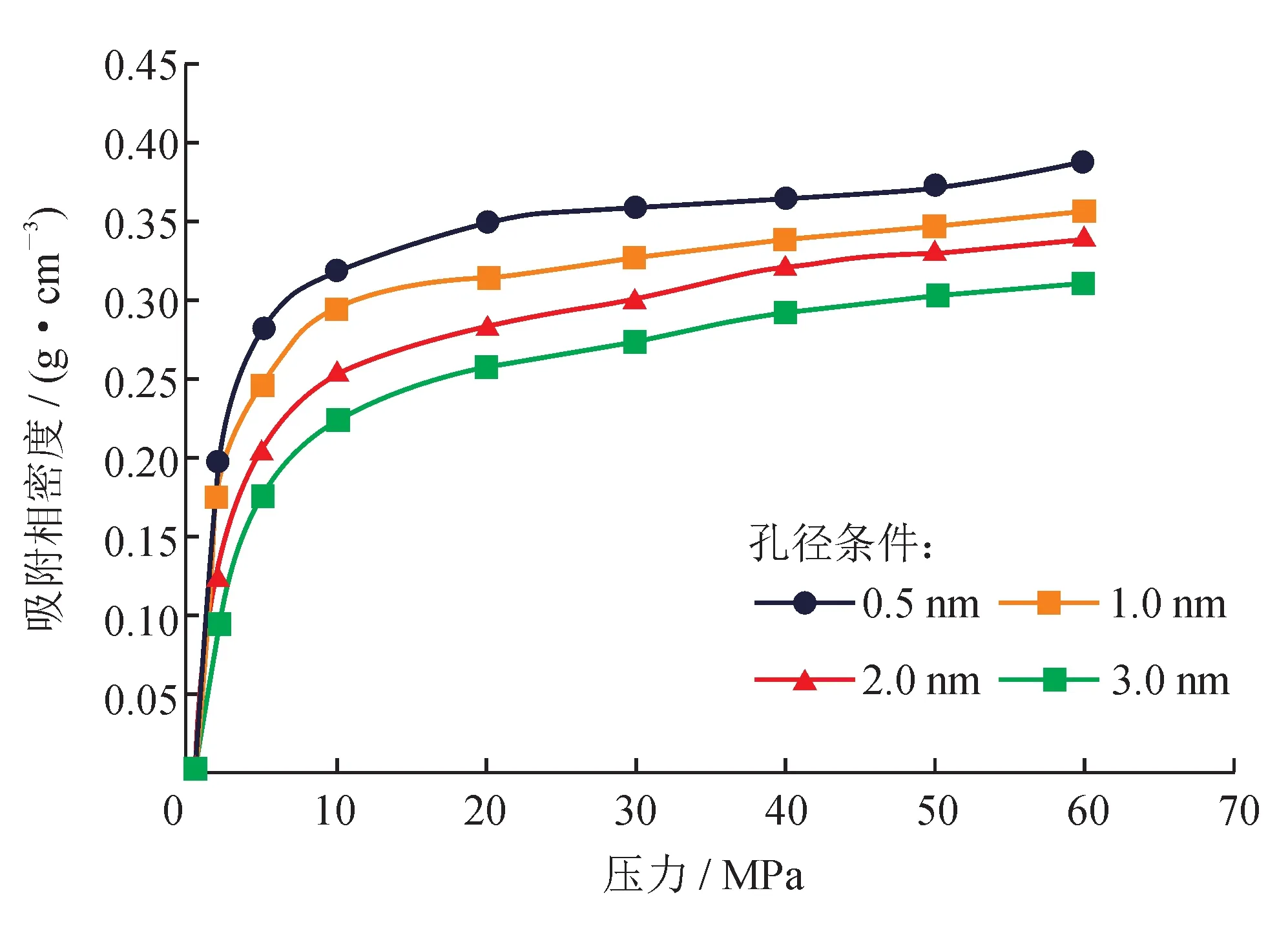
图4 压力与吸附相密度关系图

由图4 可以看出，在相同孔径的条件下，随着压力的增加，吸附相密度逐渐增大，在压力大于20 MPa 以后吸附相密度大小趋于稳定。随着压力的增加，甲烷分子被吸附的量也越大，但由于有机质表面的吸附空间是一定的，当压力增大到一定程度以后，随着压力的升高，有机质孔隙表面空间全部被甲烷分子所占据，此时孔隙表面将达到吸附量的最大值。

3.3 孔径大小对吸附相密度的影响

分别模拟了7 组不同孔径大小（0.5 nm、1.0 nm、 2.0 nm、3.0 nm、10.0 nm、20.0 nm、40.0 nm）条件下的吸附相密度。因为分子间存在极限距离以及甲烷分子本身的大小等原因，0.5 nm 孔径内最多只能容纳一层甲烷，且两侧孔壁对甲烷施加的吸附作用力叠加在一起使得甲烷吸附相密度很高，平均吸附相密度为0.269 g/cm3。而对于大于2.0 nm 孔径，由于甲烷分子之间也存在吸附作用，部分甲烷吸附在靠近孔壁的甲烷分子层上，形成了两个甲烷吸附层。随着压力的升高，还可能形成多分子层吸附。

模拟结果进一步证明，压力不变时，随着岩石孔径的增大，吸附相平均密度逐渐减小，两者呈较好的幂指数关系（图5）。页岩中孔径大小对甲烷吸附状态的影响至关重要。因此，在对页岩吸附气含量的估算中有必要考虑页岩孔径大小及其分布比例。

图5 孔径与吸附相密度交会图

4 等温模型修正

根据模拟结果可知，孔径大小对吸附相密度的影响较大。因此需要对等温吸附模型进行不同孔径分布比例的修正。

利用核磁实验数据计算孔径分布，首先实验得到核磁共振T2谱分布，然后根据T2时间和平均孔半径的关系得到孔隙直径（d）。即

式中ρ 表示表面弛豫强度，nm/ms；S 表示岩石孔隙总表面积，nm2；V 表示孔隙体积，nm3。

将上式改写为：

式中d 表示孔隙直径，nm。

令C=4ρ，则

式中C 表示模型参数。

根据资料显示四川地区龙马溪组页岩孔径分布最优C 值为4.56[27]。利用C 值求取岩样的核磁共振法孔径分布曲线，结果如图6 所示。根据分子动力学模拟结果将孔径划分为3 种类型分别为：d ＜2 nm，2 nm ≤d ≤20 nm，d ＞20 nm。分别计算出核磁共振法不同孔径平均所占比例，其结果如表3 所示。

根据Gibbs 的定义，过剩吸附量与绝对吸附量之间的转换关系为：

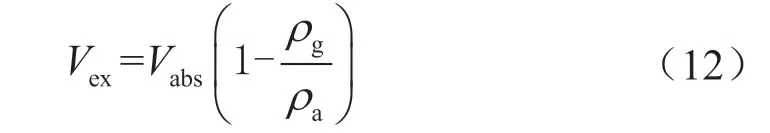
式中Vex表示某压力下的过剩吸附量，m3/t；Vabs表示某压力下的绝对吸附量，m3/t；ρa表示甲烷的吸附相密度，g/cm3；ρg表示某压力下的气体相密度，g/cm3。

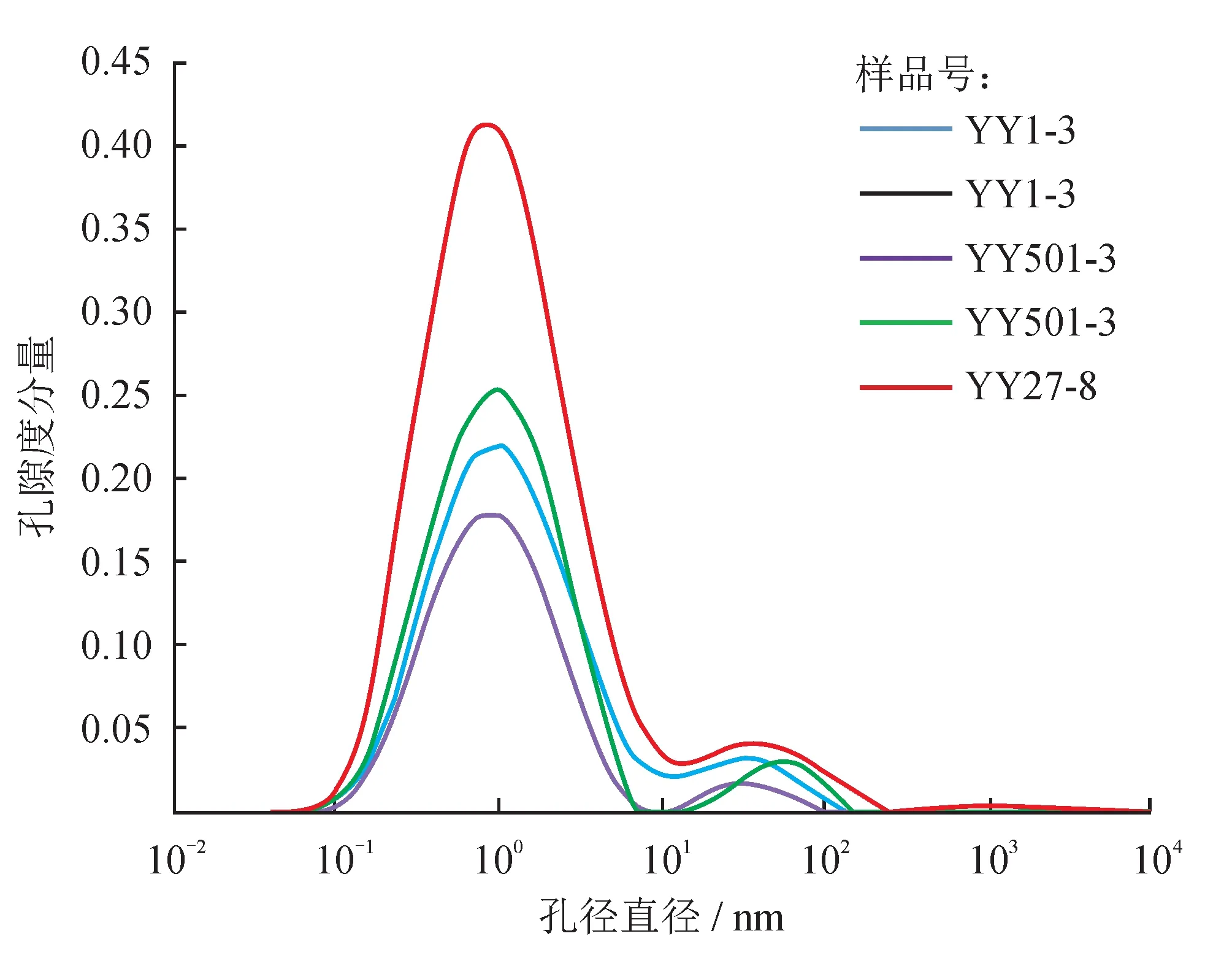
图6 核磁共振法孔径分布图

表3 不同孔径分布平均所占比例表

根据孔径分布比例，将式（12）修正为：

由于等温吸附曲线都是通过岩心样品在某一恒定温度、特定有机碳含量的条件下测得的，而实际地层的有机碳含量和温度是随深度而变化的[28]。考虑到温度与有机碳含量对页岩吸附气量的影响较大，因此，为了得到不同深度的吸附量参数，有必要进行温度、有机碳的校正，以符合实际地层的特点[29]。

校正公式为：

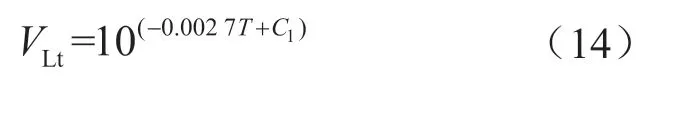
式中VLt表示经温度校正的Langmuir 体积，m3/t；pLt表示经温度校正的Langmuir 压力，MPa；C1、C2分别表示过渡变量；T 表示储层温度，℃；Ti表示等温线温度，℃。

总有机碳含量校正公式为：

式中VLc表示经过有机碳校正后的Langmuir 体积，m3/t；TOCiso表示实验总有机碳含量；TOClog表示测井总有机碳含量。

经过上述校正后的兰格缪尔方程如下：

式中Va表示吸附气含量，m3/t；p 表示储层压力，MPa。

修正得到过剩吸附量为：

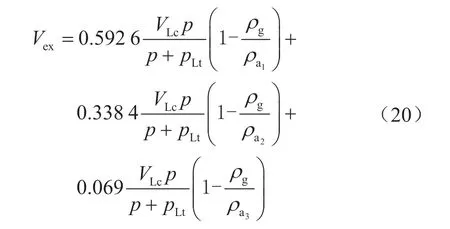
根据上述的模拟结果，结合页岩孔隙大小常规分类标准：微孔（小于2 nm）、中孔（介于2 ～20 nm）及大孔（大于20 nm），将模拟的孔径分布按上述3 段分类进行拟合，得到吸附相密度计算公式。同时，考虑到现场实际应用中，因缺乏实验和核磁资料而无法获得页岩实际孔径分布时，也可以采用平均吸附相密度公式来计算，即以图5 中每个孔径段的中间孔径所代表的密度值作为该孔径段的平均密度值（表4）。

表4 不同孔径分布的吸附相密度计算公式表

将表4 中不同孔径分布的吸附相密度计算公式带入式（20）中，就得到了基于分子动力学模拟修正的吸附气量计算模型。

采用未经修正的Langmuir 和经吸附相密度修正的模型对研究区吸附气量进行估算，结果如图7 所示。未经修正的模型计算的结果与实验室测试吸附气量结果相差较大，误差41.7%，说明未修改模型已经不能够用于精确计算页岩吸附气量（图7-a）。经吸附相密度修正的模型计算的结果在整体趋势上与实验室测试吸附气量结果基本一致且误差在7.5%以内（图7-b），说明经过吸附相密度修正后的模型的计算精度得到了较大的改善，更适合实际地层的页岩气含量计算。

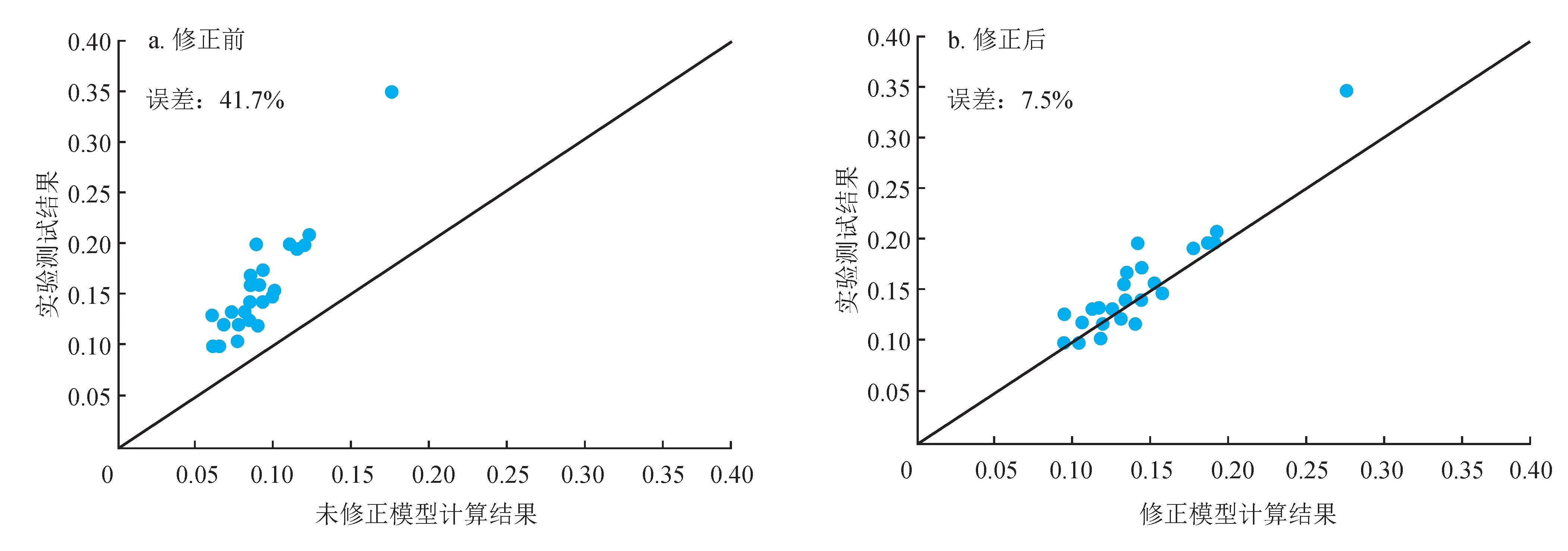
图7 计算含气量模型精度检验图

利用吸附相密度修正模型对鄂尔多斯盆地YA 地区长7 段页岩储层进行了处理（图8）。图8 中第5道为甲烷吸附相密度修正前、后计算结果以及实验测试结果的对比道。图中显示，针对甲烷吸附相密度修正模型的定量计算结果与实验测试结果相比，误差范围介于12.07%～10.38%，平均为11.23%，说明该模型具有一定的精度，能够用于页岩吸附气量的评估与计算。而未修正模型计算结果差值最大超过40%。对研究区4 口井修正前、后计算结果做误差分析，误差统计表显示修正后计算结果比修正前平均误差减小了22.74%（表5）。这表明使用修正后的模型计算页岩储层的吸附能力精度更高。

表5 研究区4 口井修正前后模型计算结果的误差统计表

5 结论

1）模拟结果表明，页岩中孔径大小对甲烷吸附状态的影响至关重要，因而页岩吸附气含量的估算必须考虑页岩孔径大小及其分布比例。

2）对超临界态甲烷吸附进行分子动力学模拟，根据模拟数据可建立不同孔径大小下的甲烷吸附相密度模型。

3）利用吸附相密度修正等温吸附模型计算的页岩吸附气量，因考虑了页岩孔隙大小非均质性对页岩吸附能力的影响，从微观上更能体现页岩在超临界状态下对吸附相的吸附特性，因而修正模型的计算结果与实验测试结果更加吻合。