基于局部通信的有限元分析并行算法优化研究

吴建平，蒋 涛，彭 军，银福康，杨锦辉

(1.国防科技大学 气象海洋学院，长沙 410073； 2.国防科技大学 计算机学院，长沙 410073)

1 引 言

连续问题一般难以直接进行求解，为此，通常采用有限差分、有限体积及有限元等方法进行离散求解。有限元法将连续的求解区域离散为一组数量有限且按一定方式相互联结的单元，典型的单元形式为多边形，其顶点称为结点。各单元之间可以存在面、边或节点的重合，同时，单元本身可以采用不同形状，并在每个单元内采用假设的近似函数，以分片方式表示整体上的未知函数，未知函数及其导数在各个结点上的值作为求解时的未知量，即自由度，从而使一个连续问题转化为自由度有限的离散问题。

由于有限元方法不受计算对象在几何、物理与边界条件上的限制，且计算精度高、使用灵活，因而自最初主要针对弹性力学与结构分析以来，已逐步扩展到航空、航天、造船、建筑、机械、海洋、气象、水利、核能和地质等众多应用领域。在采用有限元离散求解时，如果是采用时间依赖的微分方程建模的问题，且对时间采用隐式时间离散，或者是金属成形与结构疲劳分析与损伤等非线性与动态问题，则一般还需要求解线性方程组。因此，有限元离散的一般计算过程可以描述为

uk + 1=uk+(Kk)-1{Nk(uk)+pk}

(1)

式中uk为第k次迭代时的未知向量，pk为第k次迭代时的已知向量，Kk为第k次迭代时的总刚度矩阵，Nk为计算uk影响的线性或非线性算子，且

(2)

(3)

式中Ge为单元e的结点到全局结点的映射，如对单元e的第m个结点，其对应的全局结点编号为n，则Ge第m行第n列上的元素为1，该行中其他元素全为0。

由式(1)可知，有限元分析的一般过程如下。

(3) 计算Nk(uk)，其一般通过先从uk得到每个单元对应结点上的值，再通过单元上的计算，得到每个单元的贡献，最后对贡献进行累加得到最终的总贡献。

(4) 求解式(1)右端第二项所对应的稀疏线性方程组，并计算得到uk + 1。

前三步为与单元对应的计算，最后一步为与结点对应的计算。因此，在具体实现时，采用的数据结构可以分为单元与结点两类，以适应于每类计算各自的需要。在并行计算时，可以在进行单元对应计算时，按单元进行数据分布，在进行节点对应计算时，按节点进行数据分布，并在两类计算之间进行数据重分布，来进行整体上的并行算法设计[1,2]。在此整体设计框架下，在并行计算时，有限元分析中与通信有关的核心算法如下。

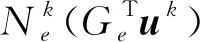
(2) 刚度矩阵的并行装配。该操作可以通过在本任务局部，先对其上所有单元完成刚度矩阵的装配，之后再将每个任务上的结果装配成总刚度矩阵。总刚度矩阵必须按行分布到每个任务上，其分布方式对应于结点在任务上的分配方式。

(3) 单元贡献的并行装配。每个任务上逐单元计算并通过对其上所有单元进行累加，得到部分结果{Nk(uk)+pk}m，其中m为任务号。之后，对这些部分结果进行累加，形成总的Nk(uk)+pk。由于{Nk(uk)+pk}m不仅含有分布在本任务上的分量，还可能含有分布到其他任务上的分量。因此，同一分量可能在多个任务上具有局部结果，这些局部结果需要进行累加。

(4) 稀疏线性方程组的并行求解。由于对三维问题或者规模很大的问题，采用迭代法求解相对更为有效且容易控制，因此这里考虑迭代法。这种方法的并行计算可以从整体上按矩阵行数平均分布的方式来进行，每个向量的分量也对应地进行平均分布，其中用到的内积与范数在每个任务上均进行存储，采用多进程规约从每个任务上的局部结果得到最终结果。一般在迭代中均会采用预条件技术，加快收敛速度[3,4]，因此，此操作中除内积与范数计算外，预条件的应用与稀疏矩阵稠密向量乘也可能需要通信。由于预条件种类繁多，这里不考虑其通信优化问题，在实验中也只采用简单的分块型并行预条件。按数据分布规则，求解所得向量在每个任务上也平均分布。

有限元分析的并行计算牵涉到诸多问题，吸引了很多学者进行研究。刚度矩阵的装配是有限元分析并行计算中最复杂的问题之一，Rezende等[5]对该问题给出了一种共享存储并行算法，刚度矩阵按有限元网格中每个节点进行分组装配，每个处理器只装配与特定节点组对应的行，有效缓解了处理器对同一内存单元的同时更新。Unterkircher等[6]提出了一种基于图论的并行装配算法与线性方程组求解算法，装配算法不依赖于维数、单元类型与模型形状，且在线性方程组求解器中引入了一种乘性对称Schwarz预条件，并通过三维金属挤压过程模拟，验证了所提出方法的有效性。Cecka等[7]针对NVIDIA GPU，提出了采用CUDA，并使用全局、共享和本地内存来进行并行装配的多种策略，通过与串行装配对比进行了实验验证。Fabrice等[8]对地震波在非线性非弹性地质中传播的有限元数值模拟，采用基于混合并行的直接求解器Pastix，以及基于网格着色与MPI_Allgather进行了并行装配算法设计，并以法国里维埃拉地区尺度模型为对象进行了实验验证。Jansson[9]对装配过程采用对总刚度矩阵的每一行采用一个链表的数据结构，并采用基于PGAS的单边通信对每个处理器上所得局部装配结果，通过远程复制来完成最终装配。

Johan等[1]对计算流体力学有限元方法在CM-2与CM-200上的并行计算进行了研究，利用预条件GMRES与数据结构进行了仔细考虑，并利用CM上提供的通信原语进行了实现。Sonzogni等[10]针对机群系统，对PETSc-FEM库进行有限元并行计算的代码实现进行了研究，并对laplace方程与NS方程的实现性能进行了测试分析。Kennedy等[11]对大规模基于梯度设计的结构优化问题，描述了一个并行有限元分析框架工具，并着重研究了其中稀疏线性方程组的并行直接求解算法。

Wu等[2]针对混凝土试件的细观力学有限元分析，进行了分布存储并行算法框架整体设计，并针对其中刚度矩阵装配、稀疏线性方程组求解及稀疏向量求和等核心问题，采用稀疏数据结构及MPI_Alltoall及MPI_Allgather等进行了并行算法的具体实现。本文主要以该工作为基础，对其设计思想进行梳理，并对其中核心算法存在的全局通信等问题，采用局部通信和计算通信重叠等技术，进一步优化有限元分析的并行计算效率。

2 刚度矩阵并行装配算法的优化

文献[2]描述了一种对刚度矩阵进行并行装配的算法，其基本思想可以描述为,先每个任务按其上单元进行局部刚度矩阵装配，得到局部总刚度矩阵。之后，将各任务上的局部总刚度矩阵累加起来，形成总刚度矩阵，并在每个任务上存储其若干行，这两步操作描述如图1所示。最后，为便于进行预条件构造，再对各行中的元素按列号从小到大排序。

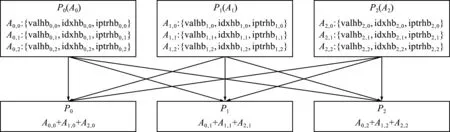
图1 三个任务时的刚度矩阵并行装配算法

可以看出，假设第k个任务上的局部矩阵记为Ak，Ak用CSR格式[3]存储在valhbk,idxhbk和iptrhbk中。由于每个任务上最终只存储矩阵中给定的若干行，记行数为nk，所以在任务k上将Ak(valhbk，idxhbk，iptrhbk)分成p组，记为Ak,j(valhbk,j，idxhbk,j，iptrhbk,j)，j=0～p-1，分别对应于Ak的nj行。之后，需要在任务j上得到所有Ak,j(valhbk,j，idxhbk,j，iptrhbk,j)，k=0～p-1之和。为达到此目的，可以采用MPI_Reduce_scatter来实现，但需要注意到，这里每个Ak,j都是稀疏矩阵块，采用CSR数据结构valhbk,j,idxhbk,j和iptrhbk,j进行存储，因此，通过采用MPI_Alltoallv将所有valhbk,j,idxhbk,j和 iptrhbk,j收集到任务j上再进行求和来实现。

在将所有valhbk,j,idxhbk,j和iptrhbk,j收集到任务j上时，假设用val,idx和iptr三个数组且采用CSR格式存储,来一次存储第k=0,1,…,p-1个任务上接收到的数据，其中val依次存储非零元素的值，idx依次存储这些非零元素的列号，iptr记录每行第一个非零元存储在val与idx的起始位置。图2 给出了对3个任务时，第k个任务上将接收到的数据存储到val、idx和iptr的示意图，其中从每个任务接收到的矩阵块均为nk行，因此，iptr的维数为3nk+1，其第一个元素表示矩阵块A0,k在val与idx的起始位置，第nk+1个元素表示矩阵块A1,k在val与idx的起始位置，第2nk+1个元素表示矩阵块A2,k在val与idx的起始位置。本文需要在任务k上先确定第A0,k,A1,k,A2,k在val与idx的起始位置以及各Aj,k内每行的起始位置，后者通过对idxhb进行MPI_Alltoallv操作来实现。对前者，先在任务k上确定各Ak,j的总非零元个数lengsk,j，再通过MPI_Alltoall得到任务k上接收到的各Aj,k中非零元个数lengrk,j。

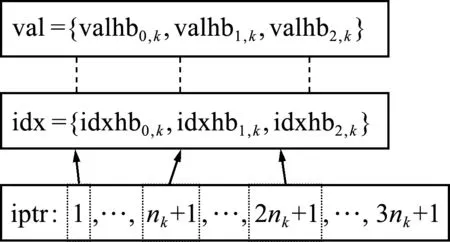
图2 三个任务时任务k上对所接收矩阵块进行存储

为对接收到的矩阵块进行求和，引入额外的整型数组cbpos，cpos和cptr来链接val，idx和iptr所记录元素中所有行号相同者，其中cbpos(m)为第m行第一个非零元素在val与idx的位置，cpos(k)为第m行中当前正在操作的非零元素所在位置，cptr(k)为与位置k对应元素处于同一行的下一个元素所在位置。采用这种稀疏数据结构，便于从val与idx中逐行提取非零元素。在对同一行中具有相同列号的元素进行累加后，即可得到总刚度矩阵的该行数据。

在经过以上操作后，实际上已形成总刚度矩阵，且每个任务上存储了应该存储的矩阵块，但现在每个矩阵行中所存储的元素是无序的。为使得各行中元素按列号从小到大的顺序排列，先将CSR格式的局部矩阵转存为CSC格式，这样局部矩阵就逐列进行存储，列号从小到大，同时，在同一列内，各行上的元素也按行号从小到大的顺序进行存储。之后，将CSC格式再次转存为CSR格式，就得到了所需的按行分块存储的整体刚度矩阵。

值得注意的是，本文主要考虑离散网格不变且需要反复进行迭代的问题，因此，在前面所述算法中，所有整型信息只需要在起始阶段进行处理，所得结果在后续迭代中直接使用。如无特别说明，这也适用于本文后续算法的描述。

前面所述刚度矩阵并行装配算法在通信时以MPI_Alltoallv为基础，这一方面将涉及到每个任务到另外每个任务之间的通信与同步，因此，所涉及的任务是全局性的，当进行大规模并行计算时，其个数很多。另一方面，这也不利于隐藏通信开销。因此，这种方式必将对并行计算的可扩展性形成不利影响。这里引入局部通信操作来替代MPI_Alltoallv的功能，基本思想是，在每个任务k上，依次判断其上第j=0,1,…,p-1个矩阵块的非零元个数，当lengsk,j≠0且j≠k时，才启动到任务j的发送操作；当lengrk,j≠0且j≠k时，才启动到从任务j接收数据的操作。这些发送与接收操作采用非阻塞式函数MPI_Isend与MPI_Irecv来实现，并在将valhbk,k，idxhbk,k和iptrhbk,k复制到val，idx和iptr相应位置上后，再等待这些通信操作的完成，以实现本地操作与通信的重叠。

3 稀疏矩阵稠密向量并行乘的优化

稀疏矩阵与稠密向量相乘在稀疏线性方程组的迭代解法中很重要，其计算时间与稀疏矩阵中的非零元个数成正比。按前文所述数据分布规则，在进行稀疏矩阵A与稠密向量x的乘法，以得到结果y的过程中，每个任务上都只具有A的部分行，且存储x和y的局部分量，文献[2]给出了与之对应的矩阵向量乘并行算法，其基本做法是将A分为p个行块，x和y也都分成为p块，其第k块分别记为Ak，xk和yk，k=0,1,…,p-1，其分配到任务k上。这样，在任务k上计算yk的数据相关性如图3所示。

图3 三个任务时的稀疏矩阵与稠密向量并行乘法

显然，进行yk的计算时，似乎需要用到其他所有任务上的x分量。但事实上，由于在计算y的某一个分量时，其等于A中对应行与x的内积，因此，只需要计算该行中每个非零元与x中相应分量(标号等于非零元列号者)的乘积之和。对任务k，只需要统计所存储Ak中所有非零元素的列号，再分析哪些列号对应的x分量不在任务k上，再获取这些分量，这就是y=Ax的通信结构。

具体地，先分析yk依赖于x的哪些分量，这些分量又处于哪些任务上。这些数据可以采用类似于稀疏矩阵的存储方法存储在idxr中，利用iptrr(j)记录依赖于第j个任务上的首分量在idxr的位置，并利用lengr(j)记录所依赖的任务j上的分量个数，其值等于iptrr(j+1)-iptrr(j)。如图4所示，图上部idxr与lengr的两个下标中，第一个为其所在任务的标号，第二个为需接收分量对应的源任务号。图下部idxs与lengs的两个下标中，第一个为其所在任务号，第二个为需发送分量对应的目的任务号，且括号中所列参数为其上参数的对应数据，即lengsj,k=lengrk,j且idxsj,k=idxrk,j。因此，idxs与lengs信息可以利用mpi_alltoall来获取。之后，利用lengs即可计算出需要发送给其他每个任务的分量在idxs的首地址iptrs。

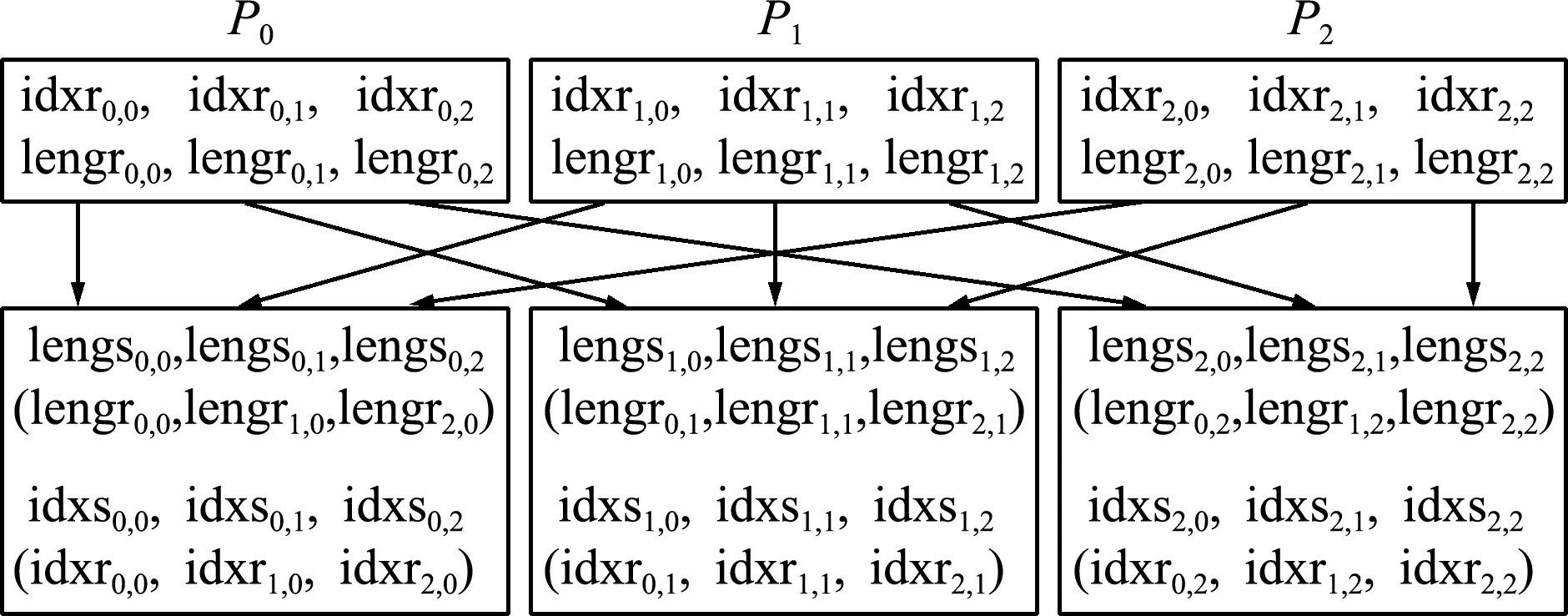
图4 三个任务时稀疏矩阵向量乘中分量对应参数交换

在计算y=Ax之前，需先收集本任务要用到的x分量，可以先在每个任务上利用idxs逐一提取需发送出去的分量并存储到vals中，之后通过mpi_alltoallv操作，在每个任务上将接收到的数据存储到valr，再将valr的元素存储到临时数组w中，使得w(idxr(j))=wr(j)。这样，就可以直接计算yi=Aiw。

与刚度矩阵的装配类似，在进行y=Ax的实际计算时，这里也可以采用局部非阻塞式通信操作替代MPI_Alltoallv。对任务k，依次判断其上lengsk,j(j=0,1,…,p-1)是否等于0，当其等于0且j≠k时，才启动到任务j的发送操作；之后，再依次判断其上的lengrk,j(j=0,1,…,p-1)，当其不等于0且j≠k时，才启动到从任务j接收数据的操作。这些操作分别采用非阻塞式函数MPI_Isend与MPI_Irecv实现。

此外，采用文献[12]对矩阵向量乘中分量进行分类的方法，将每个任务上yk的分量分为内部分量和边界分量两类。内部分量的计算不依赖于其他任务上的x分量，仅依赖于本任务局部分配到的x分量，无需通信即可进行计算。边界分量至少依赖于其他任务上的一个x分量，需要在接收到所有依赖的x分量之后才能完成计算。可以将这种对分量分类的方法与局部非阻塞式通信相结合，进行计算与通信重叠，减少通信开销的影响。基本思想是，在任务k上，先对所有lengsk,j不为0且不等于k的j，启动到任务j的非阻塞式发送操作。对所有lengrk,j不为0且不等于k的j，启动从任务j的非阻塞式接收操作。其次，进行yk内部分量的计算。在非阻塞式接收操作完成之后，再进行边界分量的计算。这样，内部分量的计算就能与通信相互重叠，从而一定程度上实现对通信开销的隐藏。

4 结点分量的局地化

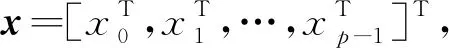
采用MPI_Allgatherv进行编程实现的方法很简单，其最终使得每个任务上都得到x的所有分量，但这带来了一些不必要的额外通信。事实上，每个单元在具体计算时，只需要用到其对应结点的分量，因此，对任务k上的所有单元进行分析，可以获知该任务在进行其上单元对应计算时实际需要依赖的分量，这一般并不会覆盖到x的全部分量，本文基于该事实，对结点分量的局地化进行优化。

将任务k上各单元在进行计算时需要依赖的结点分量分为p组，即xk,0,xk,1,…,xk,p -1。类似于第3节，将这些数据存储到valrk与idxrk，利用iptrrk,j记录xk,j首分量在valrk与idxrk的位置，并利用lengrk,j记录xk,j的分量个数，即iptrrk,j + 1- iptrrk,j。图5给出了3个任务时的示意图，显然，此时任务0上各单元的计算不会用到任务2上的结点分量，即lengr0,2=0，因此，无需从任务2接收数据。

为在各任务上获取其所含单元计算时所需数据，先对lengrk,j通过MPI_Alltoall操作，得到lengsk,j=lengrj,k，即需要从任务k发送给任务j的分量个数。之后，在任务k上，先对所有lengrk,j不为0且不等于k的j，将idxrk,j发送给任务j。对所有lengsk,j不为0且不等于k的j，从任务j接收数据并存储到idxsk,j。当进行具体结点分量的局地化时，以图5为例，在每个任务上对应的操作可以概述如下。

任务0需从任务1接收x由idxr0,1指明的分量；将x由idxs0,1=idxr1,0指明的分量发给任务1。

任务1需从任务0和2分别接收x由idxr1,0和idxr1,2指明的分量；将x的由idxs1,0=idxr0,1和idxs1,2=idxr2,1指明的分量分别发给任务0和2。

任务2需从任务1接收x由idxr2,1指明的分量；将x由idxs2,1=idxr1,2指明的分量发给任务1。

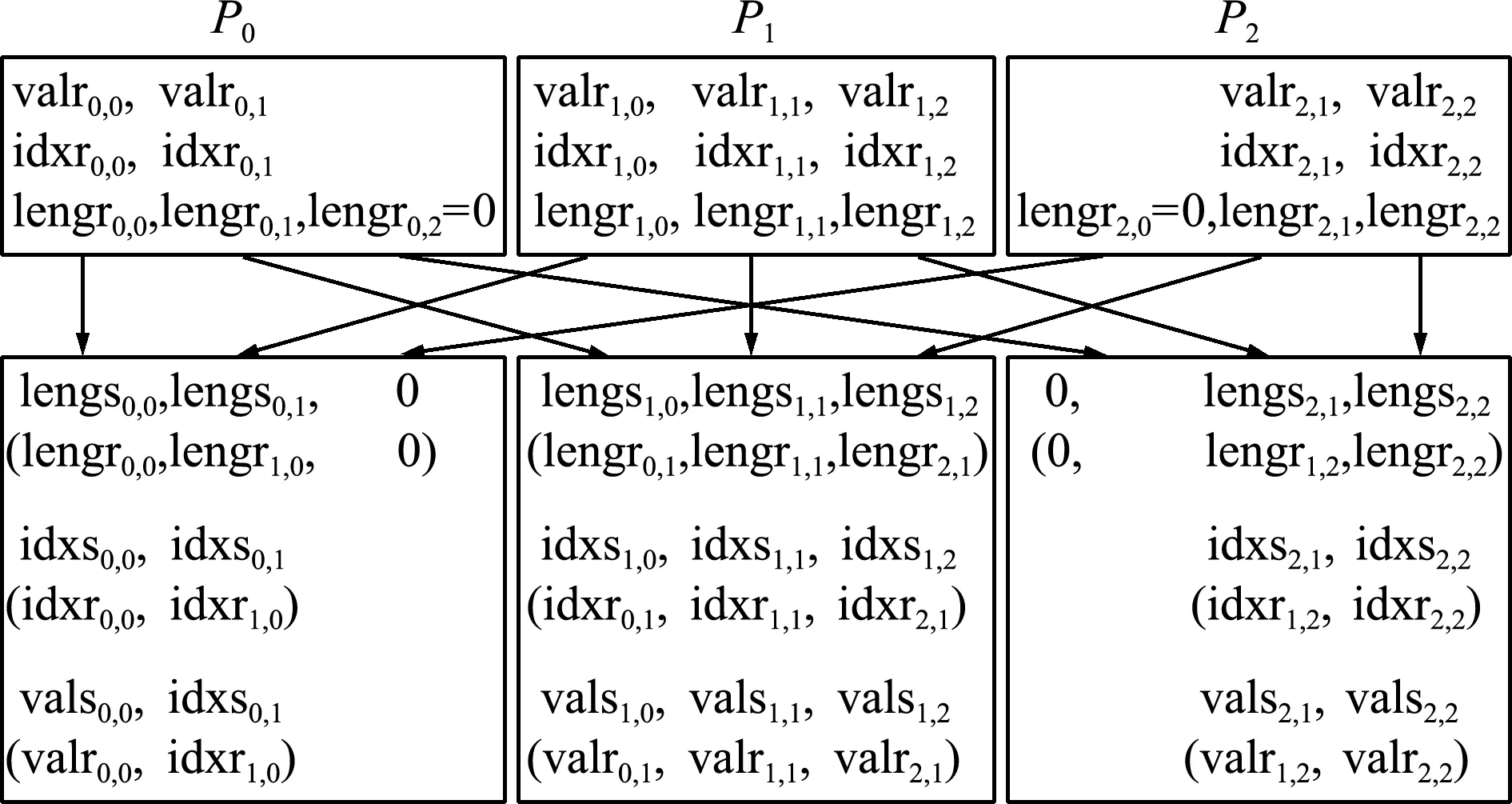
图5 三个任务上结点分量的局地化

表1给出与图5对应的一个实例，从每行看，对应的是每个任务需要从其他任务接收的x分量之指标，表中对角线位置所示为按数据分布规则分配给每个任务的分量。此时，局地化操作对应的实际上就是要按表中各列所示，从对角线处指明分量中提取各任务所需的分量。

表1 三个任务时对应于图5的结点分量局地化实例

一般地，在任务k上，可以先提取x按idxsk,j所指明的分量，依次存储到valsk,j中。其次，对所有lengsk,j不为0且不等于k的j，启动到任务j的非阻塞式发送操作，发送valsk,j。对所有lengrk,j不为0且不等于k的j，启动从任务j的非阻塞式接收操作，接收valrk,j。之后，逐步等待接收操作的完成，每完成一个接收操作，则将对应的valrk,j按照idxrk,j指明的位置复制到x中。这样，不仅通过局部通信减少了所涉及的任务个数与通信量，而且通过非阻塞式通信，一定程度上实现了通信与局地数据复制操作的重叠，从而也有利于对通信开销的隐藏。此时，每个任务进行所属单元的计算时，需要用到的x分量已全部得到。

5 单元贡献并行装配的优化

在有限元分析中，在计算单元的贡献时，需要对每个任务上的贡献进行累加，由于单元几乎平均地分配到各个任务，所以在各个任务上得到的局部向量是稀疏的。文献[2]给出了一种对有限元分析中单元贡献按稀疏向量进行并行装配的简单方法，其基本思想是，假设第k个任务上的各单元总贡献形成的局部向量为xk，用稀疏格式存储在valsk和idxsk中，之后，通过MPI_Allgatherv可以使得每个任务上都得到所有valsk和idxsk，再同时在每个任务上将接收到的valsk和idxsk叠加到本地贡献上，得到x=x0+x1+…+xp -1。

上述方法虽然思想简单，但并非每个任务均需要所有x的分量，实际上只需要得到按数据分布规则应该计算的分量即可，其他分量并不需要计算。以表1为例，此时对应的操作即是在各列中，对所有分量求和，并将求和结果存储在对角线所示任务上。本文基于该思想给出一个优化算法，其基本思想是，在任务k上，将valsk和idxsk各分成p段，分别记为valsk,j和idxsk,j(j=0～p-1)，使得idxsk,j每个指标对应分量是分布到第j个任务。显然，该操作需要的通信过程可以看成是第4节通信过程的逆过程。以图5为例，此时，在每个任务上对应的操作可以概述如下。

任务0需从任务1接收x由idxs0,1=idxr1,0指明的分量，并将其与本地x求和；需将x由idxr0,1指明的分量发给任务1。

任务1需从任务0和2分别接收由idxs1,0=idxr0,1和idxs1,2=idxr2,1所指分量，并将其与本地x求和；将x由idxr1,0和idxr1,2指明的分量分别发给任务0和2。

任务2需从任务1接收x由idxs2,1=idxr1,2指明的分量，并将其与本地x求和；需将x由idxr2,1指明的分量发给任务1。

一般地，在任务k上，可以先提取x按idxrk,j所指明的分量，依次存储到valrk,j中。其次，对所有lengrk,j不为0且不等于k的j，启动到任务j的非阻塞式发送操作，发送valrk,j。对所有lengsk,j不为0且不等于k的j，启动从任务j的非阻塞式接收操作，接收valsk,j。之后，逐步等待接收操作的完成，每完成一个接收操作，则将对应的valsk,j按照idxsk,j指明的位置加到x上。这样，既通过局部通信减少了所涉及的任务个数与通信量，又通过非阻塞式通信实现了通信与局地求和操作的重叠，从而也有利于对通信开销的隐藏。

6 混凝土细观数值模拟的实验验证

细观力学分析与研究是当前研究混凝土材料特性的热门方法之一，该方法将混凝土看作由粗骨料、硬化水泥胶体以及两者之间的界面粘结带组成的三相非均质复合材料，数值模拟是进行该型材料研究的一种重要手段。为对混凝土材料进行细观力学数值模拟，对形成的材料可以采用多种模型，这里采用随机骨料随机参数模型[15]，并采用有限元法进行离散求解，首先在细观层次上对试件进行有限元剖分，考虑骨料单元、固化水泥砂浆单元及界面单元材料力学特性的不同，再用简单的破坏准则或损伤模型反映单元刚度的退化，之后模拟试件的裂缝扩展过程及破坏形态。

本文针对2个混凝土试件的静态加载，在对有限单元进行任务划分时，将大致相同数量的连续元素分配给每个处理器。在对对应于结点的位移变量进行任务划分时，采用基于连续编号、基于离散网格和基于METIS等三种任务划分方式，实验中分别记为CONT，MESH和METIS。 对于CONT，大致相同数量的连续变量分配给每个处理器。对于MESH，变量根据相应的坐标进行分区，以便每个部分的八个部分尽可能是方形的。对METIS，变量通过metis-4.0的接口metis_PartGraphRecursive来进行划分。

所有的实验都是在64个节点的集群上进行的，每个节点有2个Intel(R)Xeon(R)CPU E5-2692 v2@2.20 GHz(缓存30720 kb)和64 G内存。操作系统为2.6.32-431.17.1-aftms-th，编译器为Intel Fortran版本15.0.0.090，节点间采用Infiniband互连，消息传递接口为MPICH 3.2.1。在所有的实验中，所遇到的稀疏线性系统都是对称正定的。因此，全部使用共轭梯度迭代。初始解为零向量，当残差向量欧几里德范数与初始向量欧几里德范数之比小于 1e -6 时停止迭代。为了加快收敛速度，使用文献[13]提供的预条件(即对称正定矩阵的ILUT版本)的块Jacobi并行化。

实验针对2个混凝土试件进行，其分别为三级配大试件和两级配湿筛试件。三级配试件的尺寸为300 mm×300 mm×1100 mm，总共离散为53200个单元，44117个结点，记为模型1。湿筛试件的尺寸为150 mm×150 mm×550 mm，总共离散为78800个单元，71013个网格点，记为模型2。关于两试件的具体描述可以参见文献[14,15]，静态加载时的有限元分析计算流程可以参见文献[15]。每步加载时荷载增量为0.25 kn。无损伤单元时，刚度矩阵与前一步相同，不需要重新装配，先前所得预条件进行重用。对某些单元在某些加载步时出现退化的非线性问题，可以通过求解多个线性方程组来解决。但在每一步的计算过程中，刚度矩阵和预条件保持不变，并进行重用。对模型1，在第439步出现损坏单元，在第567步时试件完全损坏，共求解696个线性方程组。对模型2，第59步出现损坏单元，第94步时试件完全损坏，共求解178个线性方程组。

表2列出了刚度矩阵并行装配所需要的时间，由表2可知，在任务个数不超过128的情况下，优化几乎起不到效果，优化后并行装配所耗费的时间一般反而更长，只有对试件1，在任务个数较多且采用CONT时，耗费时间得以减少。这主要是因为两方面的原因所致,一是在任务个数较少时，将全局通信操作分解为局部通信操作带来的通信所涉任务个数减少不明显;二是局地复制操作耗时很短，对通信开销的隐藏不明显。但是，在任务总数不断增加的情况下，每个任务进行通信实际牵涉到的其他任务个数变化不大，因而，在任务个数很多时，将全局通信操作分解为局部通信操作，可以有效减少每个任务在通信操作中所涉及的其他任务个数。因此，在任务个数不断增加的情况下，相比优化之前的差异程度，优化后有减小的趋势，由此可以预计，在采用更多任务时，优化算法存在减少执行时间的潜力。

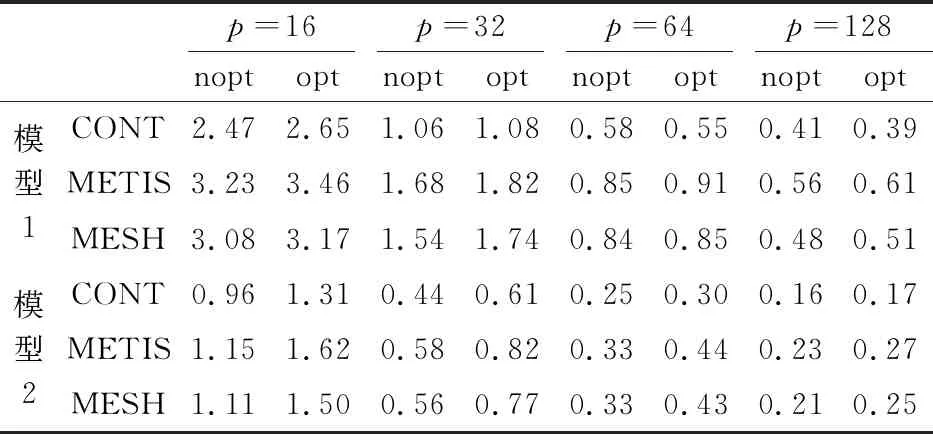
表2 混凝土试件静载实验中刚度矩阵并行装配所用总时间(单位：s)

表3列出了稀疏矩阵稠密向量并行乘所用的时间，由表3可知，无论对哪种划分、哪种试件或哪种任务规模，采用优化技术时，稀疏矩阵稠密向量并行乘所用时间均得以显著减少。同时，随着总任务个数的增加，优化后并行乘所用时间与优化前相比，总体上有不断减小的趋势，这说明总体上优化效果在任务个数较多时更明显。同时，对相同试件在相同任务个数时的模拟，相对其他两种划分算法，采用CONT算法所用时间较长。

表3 混凝土试件静载实验中稀疏矩阵稠密向量乘所用总时间(单位：s)

表4给出了节点分量局地化时所用的总时间，由表4可知，相比于优化前，优化后节点分量局地化所用时间大幅减少。在采用优化算法之前，所用时间随任务个数的增加，呈不断增加的趋势，而在采用优化算法之后，这种趋势得到了明显扭转，随着任务个数的增加，呈现出一定程度的减少趋势。

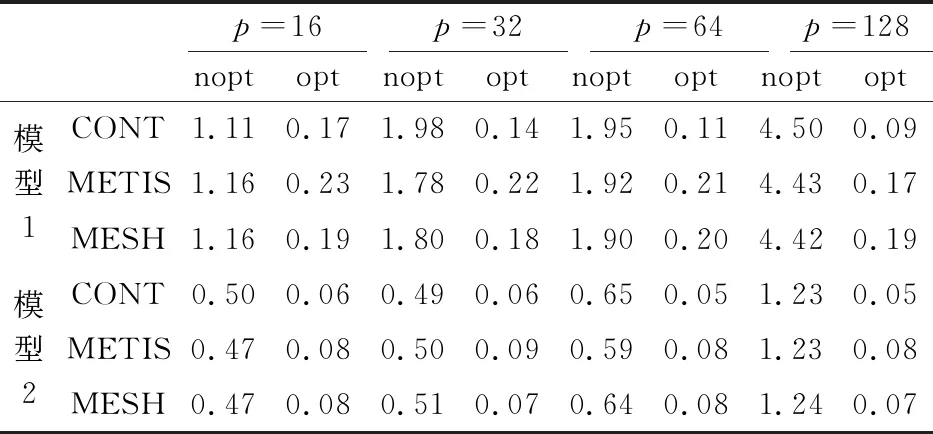
表4 混凝土试件静载实验中结点分量局地化所用总时间(单位：s)

表5给出了结点分量局地化所用的时间，由 表5 可知，相比于优化前，优化后单元贡献并行装配所用时间大幅减少。在采用优化算法之前，所用时间随任务个数的增加呈成倍增加的趋势，而在采用优化算法之后，这种趋势得到了明显扭转，随着任务个数的增加，呈现优于对折减少的趋势。

表6给出了表2～表5所列刚度矩阵并行装配、稀疏矩阵稠密向量并行乘、节点分量局地化及单元贡献并行装配所用时间之和，由表6可知，无论是对试件1还是试件2，对三种划分中的任意一种，当采用相同个数的任务时，优化后这4者的执行时间之和都明显减少。需要注意的是，对刚度矩阵并行装配，如表2所示，虽然优化算法在任务个数更多时具有潜在优势，但在所测试的任务个数下，优化后几乎没什么改进，甚至有时反而不如优化之前，但由于这一过程所用总时间相对很小，因此，对总时间没有明显影响。

表5 混凝土试件静载实验中单元贡献并行装配所用总时间(单位：s)

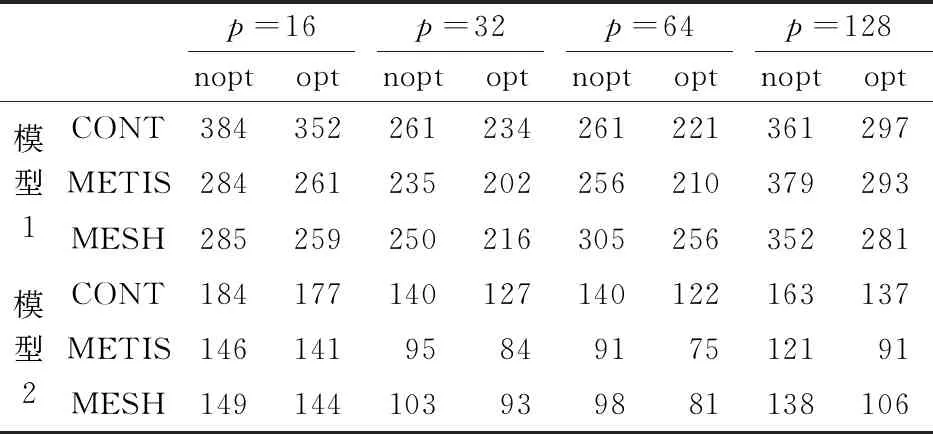
表6 混凝土试件静载实验中表2～表5所列的时间之和(单位：s)

表7给出了对每个试件，从设置阶段到加载全部完成整个过程所用时间的情况。由表7可知，无论对哪种试件、哪种划分及哪种任务数，采用优化算法极大地减少了整个数值模拟的时间。特别是在任务个数较多时，改进尤为明显。同时可见，在不采用优化算法时，对单元个数与结点个数都较少的试件1，采用64个任务时，相对32个任务已经几乎不能减少执行时间。对单元个数与结点个数稍多的试件2，虽然执行时间稍有减少，但也微乎其微。但采用优化算法时，不仅总时间相对优化前有明显减少，而且在采用64个任务时，相对32个任务，大部分情况下，执行时间得以进一步减少。对试件1，在采用CONT时执行时间能得到进一步减少。对试件2，在采用METIS与MESH时，相对32个任务，采用64个任务执行时间都得以进一步减少，说明采用优化算法还改善了整个数值模拟的可扩展性。

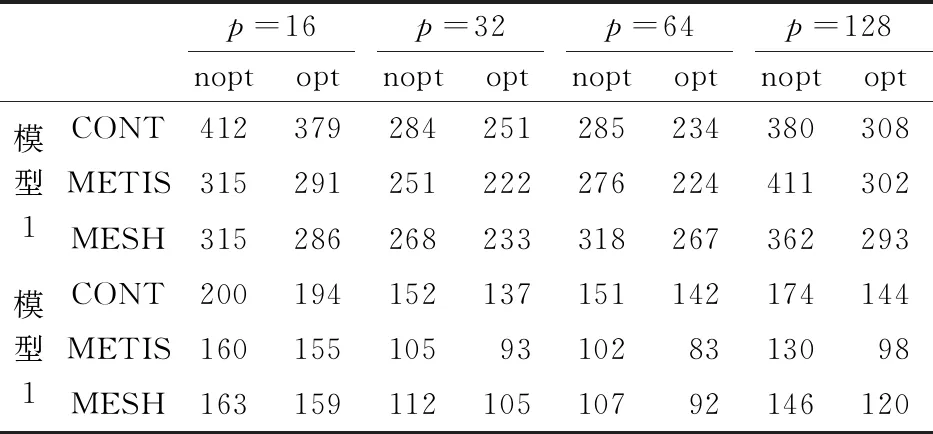
表7 混凝土试件静载实验所用总时间(单位：s)

7 结 论

本文针对有限元分析的计算问题，对其所涉核心算法通过局部通信与计算通信重叠的方式进行了优化设计，并通过混凝土试件细观力学静态加载数值模拟进行了实验验证，结果表明，无论是采用哪种任务划分，优化后相比现有算法数值模拟所用时间都得以显著减小。同时，实验验证中发现，每个任务在进行通信时，所涉及的其他任务个数都相对较多，对METIS与MESH尤其如此。这在采用局部通信操作来实现时，必然引起从同一个任务同时向多个任务发送数据，以及同一个任务同时从多个任务接收数据的通信冲突问题，如何解决该问题，对进一步采用计算通信重叠减小通信开销的影响、提高并行执行效率具有很大影响，这是下一步进行重点研究的问题。