基于自参考方法求取地磁测深响应函数

张艳辉 杨 悦

1）中国河北050043 石家庄铁道大学安全工程与应急管理学院

2）中国青岛266061 自然资源部第一海洋研究所

0 引言

地磁台站所观测到的磁场变化数据包含许多关于地幔过渡带和下地幔电性结构的信息。而通过对地球内部电性结构的研究可以探索地球的演化历史、动力学特征等问题。

Banks（1969）首先提出将地磁数据转换为C-响应函数，进而通过反演C-响应函数来研究地球内部电性结构的分布。目前被广泛应用的C-响应函数求取方法有2 种：①Z/H方法（H为水平磁场，由单一台站提供）。该方法基于球谐函数分析求解，并被应用在了研究美国西南地区的导电结构上；②Z/Y方法，垂直分量由单一台站提供，而水平分量由全球台站数据的球谐系数表示（Olsen，1999）。

国内学者对求取地磁测深C-响应做了诸多研究，并取得一系列成果。如：杜兴信等（1995）使用单台Z/H方法，分析了陕西地区深部电导率；范国华等（1997）利用梯度法，分别求取了25 个台站周期为24 h、12 h、8 h、6 h 的C-响应值；张贵宾（1998）详细介绍了地磁测深方法的原理，并采用Z/Y方法求取我国东北地区地磁台站数据的响应函数。因为地磁信号微弱，易受干扰（李雪华等，2012），所以地磁响应曲线质量较差。

BIRRP（Bounded Influence，Remote Reference Processing）是由Chave 等（2004）在Robust法基础上开发的数据处理软件。Bounded Influence 方法将标准的M 估计方法和Hat Matrix diagonal 统计分析相结合，可以由时间域的电磁场信号通过远参考方法得到稳健的频率域响应。该方法可以消除地磁场信号中的相关噪声，同时具有较高效率。

为了更好地处理中国地区地磁台站数据，将BIRRP 中使用的远参考方式改为基于本身的自参考方式，并以此求取地磁台站C-响应函数。分析验证结果显示，本方法可以得到较为可靠的地磁测深C-响应数据，为以后的科研工作奠定了基础。

1 C-响应求取的基本原理

在磁层源可以近似表示为的条件下，C-响应计算公式（Banks，1969）可以表示为

其中，α0为地球的平均半径，Hr、Hθ分别为地表处垂直指向地心和水平南向的磁场，θ为地磁余纬度，ω为角频率。关于Hr和Hθ的求取可参考Semenov 等（2012）的研究。

2 数据处理基本技术

常规地磁C-响应求取流程为：①原始时间序列中长期变化场的去除；②C-响应的求取需在地磁坐标下进行，因此进行地磁分量时间序列的坐标系旋转；③时间序列转到频率域分析，一般使用离散傅里叶变换；④按照公式（1）进行不同周期的C-响应求取；⑤海洋效应影响去除。

为了得到准确、稳定的C-响应曲线，在每一个步骤均采取不同技术手段，以保证处理过程的正确性。

此外，高纬度地磁台站数据易受极光效应影响。目前的研究并不能较好地消除极光效应影响（Semenov et al，2012）。然而，由于使用的地磁台站均位于10°—50°N 范围，受极光效应影响较小，故极光效应不予考虑。

2.1 地磁分量求取

国家地磁台网中心地磁数据存储采用IAGA（The International Association of Geomagnetism and Aeronomy，国际地磁学和高层大气物理协会）格式，包含地磁偏角D、水平分量H和垂直分量Z的绝对记录值或相对记录值，在实际使用时一般需要将数据转换为水平分量X、Y和垂直分量Z（图1）。而在C-响应求取中，需要使用水平南向磁场Hθ和垂直地心的磁场分量Hr（即Z）。将水平分量H分解得到水平南向分量Hθ，即

图1 兰州台站地磁三分量时间序列Fig.1 Time series of the three components of the geomagnetic data of Lanzhou station

2.2 长期变化场去除

地磁测深研究的是磁层电流（外部场源）产生的变化磁场。地磁场的主要组成部分是起源于地球内部的长期变化场。在进行较长周期的电磁感应研究中，需要将长期变化场去除（Olsen，1999）。国际地磁参考场（IGRF）是描述地球主磁场和长期变化场的数学模型。在地球表层和上部区域，主磁场（地球内部场源引起的）各分量可以由地磁位函数V的梯度来表示

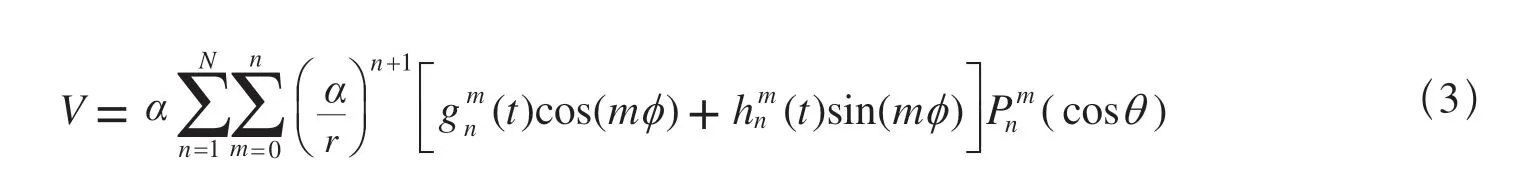
其中，φ和θ分别是经度和余纬度，α=6 371.2 km，r是地心距，N表示最高阶数，和是地磁位的球谐系数，是Schmidt 归一化缔合Legendre 函数。

IAGA 提供了计算地磁场不同分量长期变化的程序代码。该程序可用于去除各台站不同分量对应的长期变化场（https://www.ngdc.noaa.gov/IAGA/vmod/igrf12.f）。

为了验证长期变化场去除与否对C-响应求取结果的影响，从国家地磁台网中心获取部分台站的地磁数据，并将长春台（CNH）和满洲里台（MZL）去除与未去除长期变化场的C-响应计算结果进行对比（图2）。由图2 可见，长春台站数据长期场去除与否对短周期的C-响应影响不大，二者几乎重合，但在长周期段，二者存在明显差别；满洲里台站数据的计算结果显示，二者的响应曲线趋势类似，然而具体数值存在明显区别。因此，在C-响应求取过程中，有必要去除长期变化场。

图2 长春台和满洲里台长期场去除与否的C-响应处理结果对比Fig.2 Comparison of C-response results of Changchun (CNH) and Manzhouli (MZL)stations with or without secular variation removal

2.3 坐标系转换

对已知地球模型进行数值模拟时，通常假设源为地球磁层中的环形电流，并以球谐函数来表示，该电流环与地球的磁赤道同心。地磁测深数值模拟和反演均在地磁坐标系中进行。因此，数据处理时需要将地理坐标系中的磁场数据旋转到地磁坐标系中，以得到地磁坐标系中的C-响应。

坐标系旋转的基本思路为，通过国际地磁参考场（IGRF）移除长期变化场，利用IGRF 计算程序得到地磁坐标系中某点的磁偏角D，由去除长期场的Hx和Hy可得到去除长期场的H及其与地理北的夹角，通过简单加减法即可得到该夹角，也就得到了地磁北和东分量。

图3 为坐标系转换示意图，O为台站位置，H为台站观测水平磁场强度，Dobs为台站观测磁偏角（并不一定等于该点的磁坐标系与地理坐标系的夹角，因为该点的水平磁场不一定指向磁北，但在一维地球和源的条件下，取等是成立的），Hx和Hy为台站观测的地理北向和地理东向分量，Hx-sv、Hy-sv是减去长期变化场（由国际地磁参考场IGRF 计算得到）的地理北向和地理东向分量，H-sv是减去长期场之后的水平磁场强度，DIGRF是由IGRF 计算得到的磁偏角，可以认为是地磁北和地理北方向的夹角。

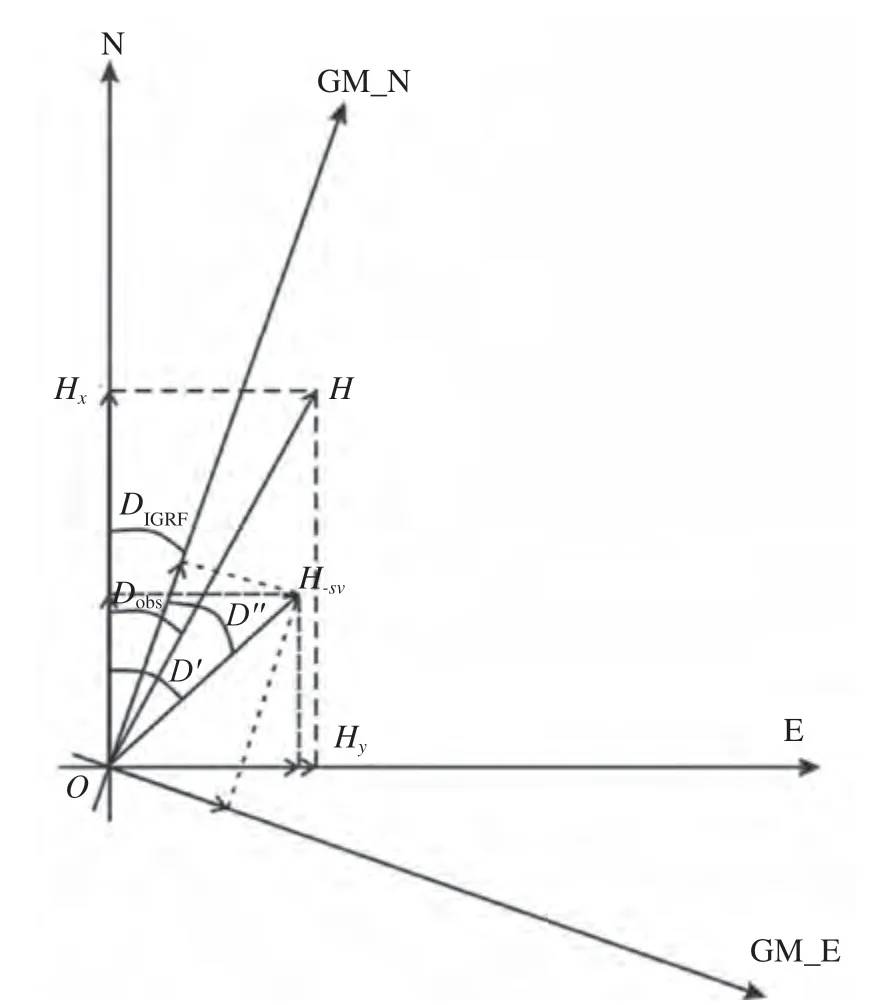
图3 地理坐标系旋转到地磁坐标系示意Fig.3 Schematic diagram of rotation from geographical coordinate system to geomagnetic coordinate system

2.4 时频转换

在进行地磁测深C-响应求取时，使用一个短的自回归滤波器对每一个时间序列进行预白化，可以有效减小频谱偏差。将数据分段，截取每个频率对应的时间段。由于常规锥形截取时间序列会造成频谱泄漏和影响分辨率，故采用Slepian 序列窗来进行数据截取（Chave et al，2004），可以通过调节时间带宽来满足不同的周期要求。

由于需要在频率域分析地磁响应，故使用离散傅里叶变换将截取的时间序列转到频率域，并采用重叠平均法来增加计算的可靠性（Chave et al，2004）。

2.5 基于Bounded Influence 方法的C-响应处理

采用Bounded Influence（BI）方法计算地磁测深的C-响应函数。Semenov 等（2012）通过对比，验证了在地磁测深数据处理中，采用台站自参考方法与远参考具有良好的一致性。因此，采用自参考方法进行C-响应的求取。

其中：H*为H的复共轭；*表示矩阵的复共轭；α=6 371.2 km，为地球半径；为叠加自（互）功率谱（Huber，1981），表达式为

式中，A和B代表不同的磁场分量或者参考分量。

为了判断不同质量数据的台站C-响应的可靠性，通过求取平方相关系数和数据误差来进行C-响应质量评价。在实际数据处理中，可以去除相关系数较低或数据误差较大的响应数据。

在计算得到C-响应之后，本文按照Semenov 等（2012）的方法计算了C-响应不同周期的平方相关系数。

其中，H*、Z*分别表示H和Z的复共轭。C-响应的数据误差计算式（Schmucker，1999）为

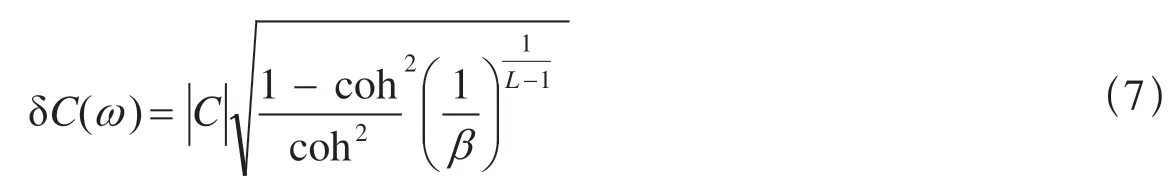
其中，1-β是置信水平，本文的置信水平设置为0.9（Chave et al，2004）；L是时间序列的分段数量，周期越长，L越小。

3 台站数据处理结果

我们利用上述方法对ASP（Alice Springs）和HON（Honolulu）台站数据（数据下载地址：http://geomag.org/）求取C-响应并与已有结果进行了对比，见图4。可以看到本文方法处理得到的响应曲线在短周期段与Semenov 等（2012）的结果保持着较好的一致性；在长周期段更加稳定，“飞点”情况明显减少。从平方相关系数和误差棒也能明显看到本方法求得的C-响应相关性系数更高，误差更小，这说明了该方法的正确性和稳定性。

图4 本方法求取的C-响应与Semenov 等（2012）结果对比三角形为Semenov 的结果；圆圈为本文的结果Fig.3 Comparison of the C-response obtained by this method with the result of Semenov et al (2012)

为了进一步检验本方法求取的地磁台站C-响应的正确性，利用从中国国家地磁台网中心获取的北京和兰州地磁台站记录数据求取C-响应，所得结果见图5。由图5 可见，2个台站数据的响应曲线稳定，且在短周期段具有较低的数据误差和较高的一致性；而在长周期段，受限于数据记录长度，无论是平方一致性曲线还是数据误差以及C-响应曲线的连续性均相对较差。整体而言，利用该方法可以为中国地磁台站C-响应求取提供良好的技术支持。

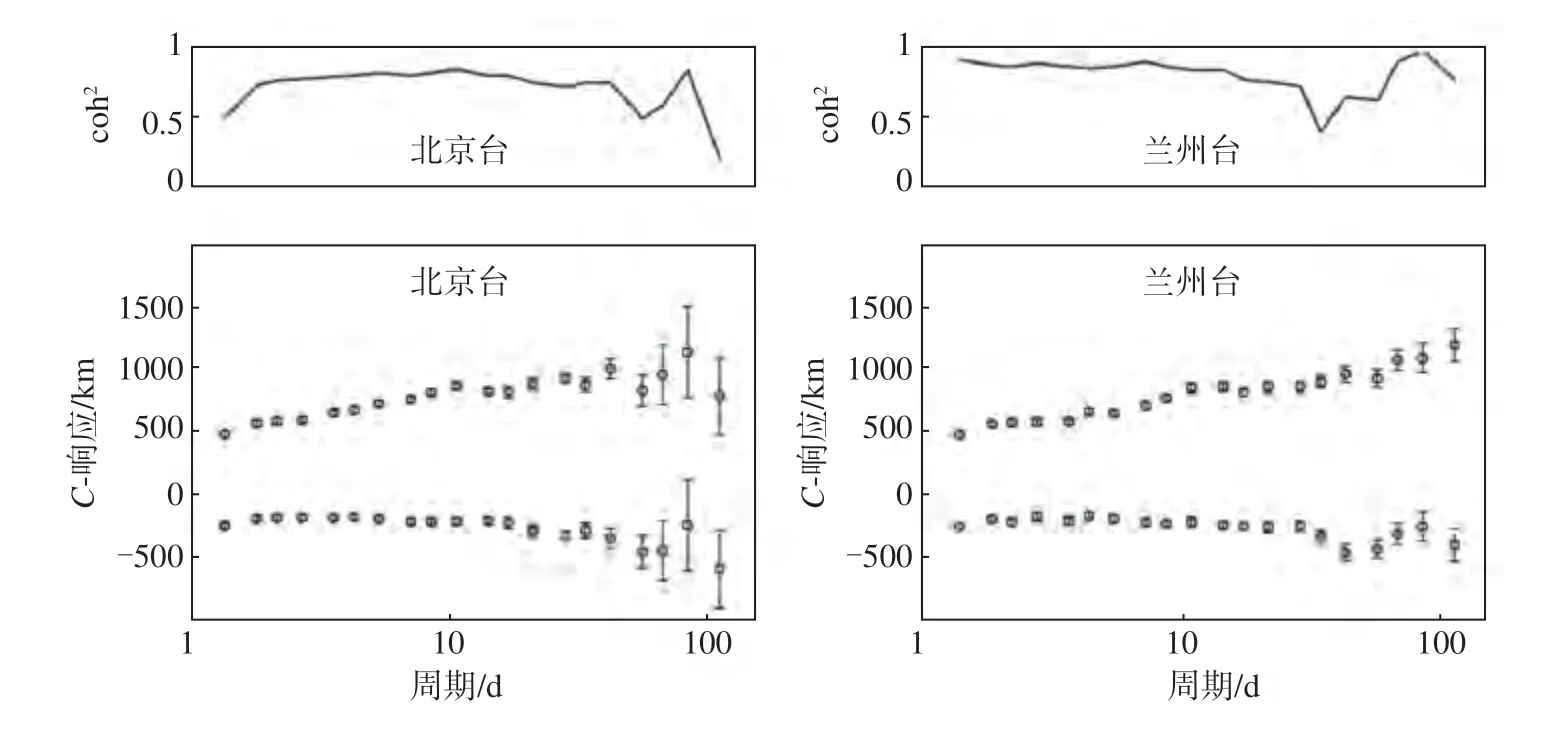
图5 使用本方法求取的北京（BJI）台站和兰州（LZH）台站C-响应和平方一致性曲线Fig.5 C-responses and square coherences curve of Beijing (BJI) and Lanzhou(LZH) stations obtained by the method in this paper

4 结论

利用自参考Bounded Influence 方法求取地磁测深C-响应值可有效减少实测地磁场数据的环境干扰和噪声影响。C-响应曲线的“ 飞点”明显减少，同时，响应曲线的平方相关系数更高、误差更小。本方法为高分辨率三维地磁测深反演研究奠定了基础。