用P波初动资料确定地震震源机制教程（四）

陈运泰 刘瑞丰

1）中国北京100049 中国科学院大学地球与行星科学学院

2）中国北京100081 中国地震局地球物理研究所

4 确定震源机制解的图解法

为了从观测资料求得地震的断层面解，即震源机制解，可以按下述步骤（Кейлис-Борок，1957；Balakina et al，1961a，b；Stauder，1962；Bollinger，1968；Herrmann，1975；Brumbaugh，1979；Udias et al，1985；Udias and Buforn，1988；Udias，1991，1999；Shearer，1999；Bormann，2002）求得.

4.1 准备工作

4.1.1 资料准备.首先要搜集准备有关资料，包括：震中位置坐标及震源深度、地震台站坐标及海拔高程、发震时刻、震级、震中距、震中指向台站的方位角、主要震相的到时读数.通常，这些资料可由地震报告得到.同时，由地震资料中心得到所研究的地震记录（以前是模拟记录地震图，现在则是数字地震记录）.

4.1.2 确定P波初动符号.从每个地震台记录的短周期和长周期竖直向地震图中读取P波初动的极性（polarity），也即初动符号.最好是从长周期、竖直向（long period vertical，记作LPZ）地震图中读取.因为从长周期、竖直向地震图中一般比较容易确认P波初动的符号，特别是对于20 世纪70 年代以前的地震图更是如此.受到短周期噪声的干扰，从短周期、竖直向（short period vertical，记作SPZ）地震图中有时较难确认P波初动符号.如前所述，地面运动向上（up）即压缩（compression，C）、离源（anaseismic，a）、推（push），分别以u，C，a，push，“+”号或实心圆圈表示；地面运动向下（down）即膨胀（dilatation，D），向源（kataseismic，k），拉（pull），分别以d，D，k，pull，“-”号或空心圆圈表示.P波初动符号的极性有上述多种称谓与符号，是由于从不同角度描述同一现象引起的，反映了对地震震源机制认识的深化与发展.现在，已约定俗成以“+”号或实心圆圈表示初动向上，以“-”号或空心圆圈表示初动向下；并且习惯上用阴影、黑色或其他颜色的区域表示初动向上的象限，只用白色或无色但不用阴影、黑色或其他颜色的区域表示初动向下的象限.

P波初动只能在震中距小于90°—100°的距离上观测到.当震中距大于上述距离时，P波信号微弱，因为或者是发生了反射，或者不再是初至波.当震中距落在140°—167°的范围时，PKP是初至波.PKP是穿过地核的P波，这个震相在上述距离范围内清晰，比较容易确认，因此可以用来确定地震的断层面解.

深源地震所特有的震相pP和穿过地核的P震相PKP也可用于确定地震的断层面解.也有人用PP震相确定地震的断层面解.不过对PP震相的运用一直有争议，因为使用PP震相求断层面解，有时会导致错误的结果.

对于地方震（即近震），Pg和Pn震相均可用于确定地震的断层面解.

4.1.3 求离源角.离源角ih可以由下述方法求得.对于远震，即震中距Δ ＞1 000 km 的地震，离源角ih作为震中距Δ 和震源深度h的函数，即ih=ih(Δ，h)，可由时距曲线t(Δ，h)按式（3）求得：

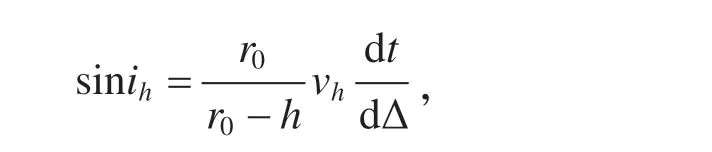
式中，r0为地球半径，震中距Δ 以长度（例如km）为单位，vh为P波在震源处的传播速度.预先计算出离源角表，即可简便地由离源角表查得ih.作为举例，表2 给出表面震源（即h=0）情况下的P波离源角表（Pho and Behe，1972）.

表2 表面震源情况下的P 波离源角表Table 2 Table of P-wave take-off angles in the case of surface source

首波Pn的射线也是下行射线，其离源角ih也就是P波在莫霍界面（Moho）发生全反射时的临界角（图32）.所以其离源角ih可由下式计算求得（Bormann，2002）：

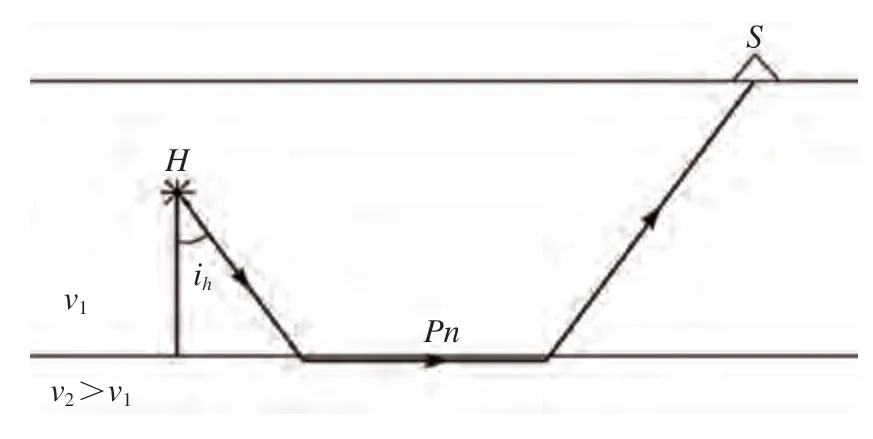
图32 首波Pn 的离源角Fig.32 The take-off angles of the head wave Pn

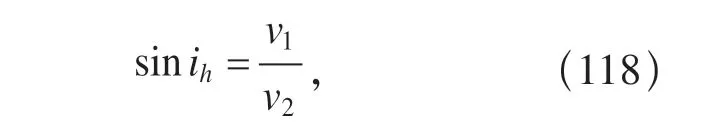
式中，v1，v2分别为P波在地壳与上地幔最上部的传播速度.根据我国大陆地壳速度结构模型，可以求得Pn的离源角约为53°.对于地方震，即Δ ＜1 000 km 的地震，首先需要知道所研究地区的地壳与上地幔速度结构，然后由地方震的走时曲线计算出相应的离源角表.地壳中地震震源深度的测定误差会导致离源角的误差大到10°左右，这一误差限制了确定断层面的精度.

4.1.4 列表.将台站代码，震中距Δ，震中指向台站的方位角φ，离源角ih，P震相的名称（是P，还是PKP，pP，pPKP，PP，Pg，Pn，等等）及其符号列成表格.

4.2 在投影图上表示假想点及其初动符号

为了在震源球的投影图上表示台站在震源球球面上假想点的投影及其初动符号，首先要决定是采用震源球上半球投影还是下半球投影.对于远震来说，因为大多数初动符号的资料来自下行射线，即离开震源向下传播、然后回折到地面台站的射线，所以宜采用震源球下半球投影.对于地方震来说，因为大多数初动符号的资料来自上行射线，所以宜采用震源球上半球投影.今以震源球下半球等面积投影为例，说明如何在投影图上表示假想点的投影及其初动符号.对于极射赤面投影，做法完全相同，只不过应采用相应的网（乌尔夫网）.图33 表示如何在震源球下半球的等面积投影图（施密特网）中表示(φ，ih)=（33.0°，53.0°）的假想点（见附表2 中序号为4 的抚顺台）.

以一张透明纸覆盖在施密特网上[图33(a)]，描下圆周，在圆周东、西、南、北四个方向标上表示方向的短线，并写上相应方向的字母E，W，S，N.此圆周便是震源球下半球的投影.为直观起见，在图33，图35 和图36 中，以天蓝色线条表示为透明纸所复盖的施密特网.图中的子午线（经圈）代表了倾角δ不同的平面，最靠边的子午线即东边或西边的两个半圆表示δ=0°的平面.随着倾角增大，δ=0°，10°，20°，…，90°，相应地，代表这些不同倾角的平面的投影是图中所示的、越来越靠近连接N和S的直线的圆弧.连接N和S的直线是对应于δ=90°的平面的子午线.为了明确起见，规定只用锐角表示断层面的倾角，所以0°≤δ≤90°.反过来，由H朝E数，则表示离源角ih=0°，10°，20°，…，90°.在施密特网上，圆周边上的数字表示方位角φ.同样为了明确起见，规定用顺时针、从0°至360°的角度表示方位角，所以0°≤φ＜360°.

为了在投影图上表示(φ，ih)=（33.0°，53.0°）的假想点，取透明纸，在纸上标注表示方位角φ=33.0°的记号[图33(a)]，将透明纸旋转，使φ=33.0°的记号与施密特网上的E重合[图33(b)].现在，透过透明纸所见施密特网的中心H至E的直线上每个点都表示φ=33.0°但离源角ih不同的假想点.从网的中心H开始，沿着赤道向东移动，ih便从0°增加到90°.在赤道上与ih=53.0°相应的点便是(φ，ih)=（33.0°，53.0°）的点[图33(b)中的小黑点].将该点的初动符号标上.初动为压缩，以C，“+”号或实心圆圈表示；初动为膨胀，以D，“-”号或空心圆圈表示.在个别情况下，有的台站的初动表现为微弱的“+”或“-”，即表现出该台站的假想点可能位于节面附近，具有“节点特性”.在此情况下，可以用“×”号表示该台站的假想点的极性具有“节点特性”.将(φ，ih)=（33.0°，53.0°）的假想点及其极性绘于透明纸上，之后便可将透明纸转回原来的位置[图33(c)].对其他假想点重复上述步骤.这样，便完成了在施密特网上表示方位角为φ，离源角为ih的假想点及其极性的步骤.

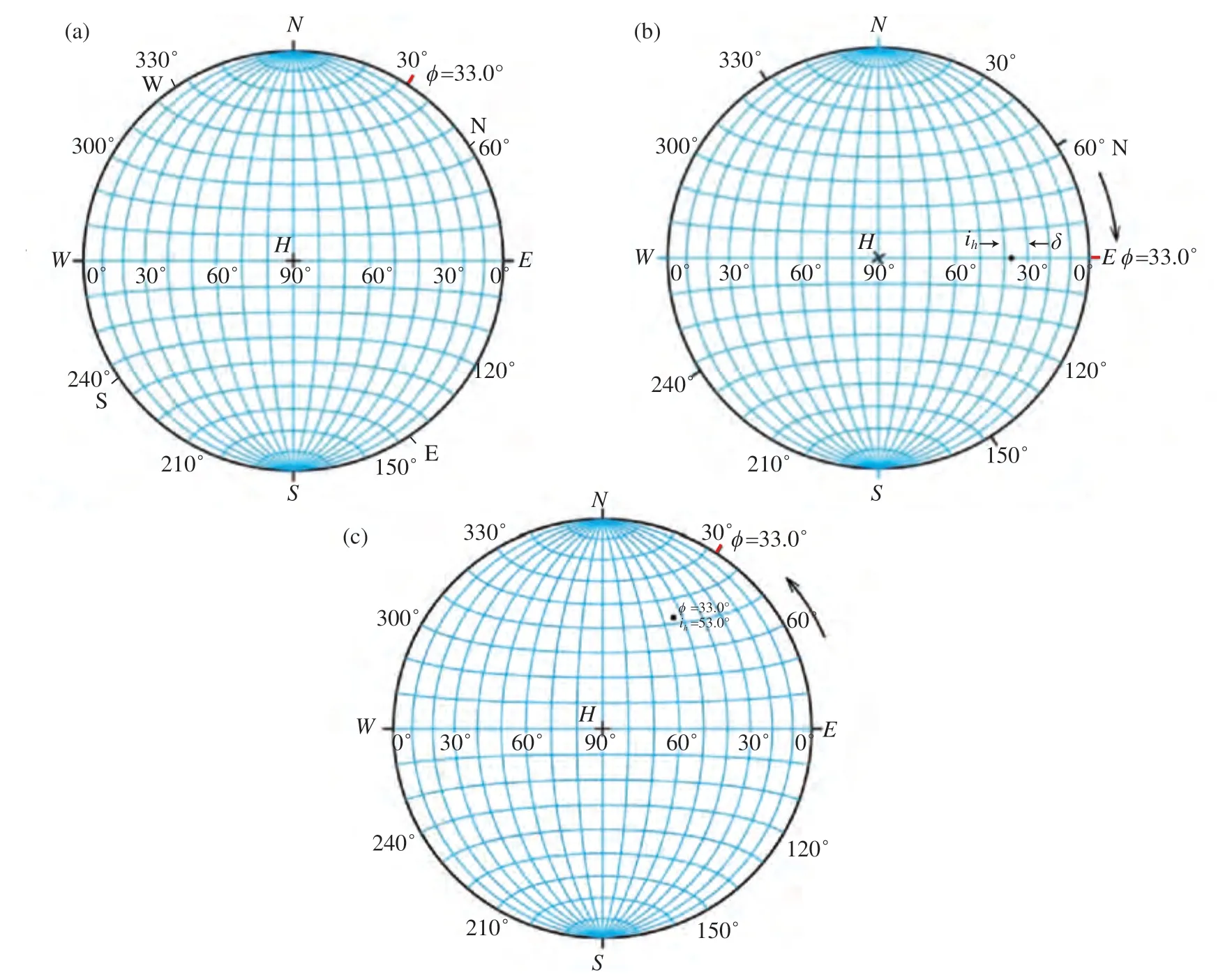
图33 在震源球下半球的等面积投影图中表示方位角为φ，离源角为ih 的假想点(a) 在透明纸上画震源球下半球的投影，并标记方位φ；(b) 旋转透明纸，标上表示(φ,ih)的假想点；(c) 将透明纸旋转回原来位置Fig.33 In the equal-area projection of the lower hemisphere of the focal sphere,the conventional point with azimuth φ,and take-off angle ih are ploted(a)Draw the projection of the lower hemisphere of the focal sphere on transparent paper and mark the azimuth φ;(b)Rotate the transparent paper,mark the conventional point with(φ,ih);(c)Rotate the transparent paper back to its geographic orientation with N at the top

4.3 震源球另一半球资料的运用

地震的断层面解具有相对于震源的中心对称性，位于震源球上半球(φ，ih)的台站（假想点），其初动符号与位于震源球下半球（φ± 180°，ih）的台站（假想点）是相同的（如前所述，在震源球上半球和下半球中，ih分别定义为离源射线与由球心向外的半径方向和指向球心的半径方向的夹角，所以ih不变；在φ± 180°中，正负号的选择是要使得0°≤φ± 180°＜360°）.因此，若按此做法采用震源球下半球投影，那么对于来自上行射线，即射线离开震源后迳直向上传播至地面台站的初动符号资料，在震源球下半球的投影中，应将该台站的初动符号表示在（φ± 180°，ih）的位置上（图34）.

图34 在震源球下半球投影图中来自上行射线的初动符号资料的应用Fig.34 Application of first motion data from upgoing ray in projection of lower hemisphere of focal sphere

4.4 确定节平面

将所有台站的位置(φ，ih)及其初动符号均画在投影图（图35）上之后，便可通过以下描述步骤继续作图以确定断层面解.

图35 所有台站的位置(φ，ih)及其初动符号均已画在投影图上Fig.35 The positions of all stations (φ，ih)and their first motion polarity symbols have been plotted on the projection

按上述步骤将所有观测资料(φ，ih)标在震源球下半球的投影图上，并标注其P 波初动的符号（“+”，“-”，“×”或“●”，“○”，“×”），之后便可开始画节（平）面.节面是两个互相垂直的、把P波初动符号交替分开成四个象限的平面.在投影图上，它们是通过彼此的极的两段圆弧.

为了画出第1 个节面，将透明纸逆时针旋转φ1角（0 ≤φ1＜360°）.在这个例子里，φ1=290.0°，此时，透过透明纸所见最东边的半圆（子午线）代表δ=0°的平面，如图36(a)中的数字所示，随着δ增加，即δ=0°，10°，20°，…，90°，代表方位角为φ1但倾角δ不同的平面的投影，是透过透明纸看到的越来越靠近连接N 和S 的直线（子午线）.图中，以黑实线表示在透明纸上画出的、表示φ1=290.0°，δ1=81.0°的节面1（NP1）的圆弧.

画出节面1 后，接着要确定它的极X，即通过震源球球心H，垂直于节面1 的轴线与震源球下半球球面的交点.该轴线的方位φx=φ1-90°或φx=φ1+270°，使得0°≤φx＜360°；倾角（plunge）即与水平面的夹角δx=90°-δ1[图36(a)].

画完节面1 并确定了它的极X后，将透明纸顺时针旋转φ1角，转回原来的位置，便得到如图36(b)所示的图.

图36 确定第一个节面NP1(a)将透明纸逆时针旋转φ1 角，画出节面1，确定X 极；(b) 将透明纸顺时针旋转φ1 角转回到原来位置Fig.36 To plot the first nodal plane NP1(a)Rotate the transparent paper anticlockwise by φ1,draw the nodal plane 1,and find the pole X；(b)Rotate the transparent paper clockwise φ1 back to the original position

节面2 是与节面1 垂直的平面.因此，画节面2 时，代表节面2 的投影的弧线（子午线）一定要通过极X=(φx，δx)（参见图37）.为此，将透明纸逆时针旋转φ2角，使得代表方位角为φ2，倾角为δ2的平面的子午线（弧线）正好过X，且与代表节面1 的弧线交替地将初动符号分成四象限[图37(a)].既然节面1 与节面2 互相垂直（正交条件），节面2 通过节面1的极X，那么节面1 一定通过节面2 的极Y=(φy，δy)，φy=φ2-90°或φy=φ2+270°，使得0 ≤φy＜ 360°，φy=90°-δ2.自然地，为了作出两个互相垂直的平面，将P波初动符号交替分成四个象限，通常要按上述步骤经过多次反复试验，直至不符合四象限分布的观测资料降到最低限度为止.

断层面解质量的优劣通常由符合四象限分布的观测资料的数目N1与观测资料的总数目N的比值S的大小来衡量，即

或者反过来，用不符合四象限分布的观测资料的数目N0=N-N1与N的比值（矛盾比）R来衡量，即

显然，

经过多次反复试验，最后求得如图37(a)所示的节面2（NP2）及其极Y.在这个例子中，节面2（NP2）是表示φ2=23.0°、δ2=75.0°的节面的圆弧[图37(a)].现在将透明纸顺时针方向旋转φ2度转回到原来位置，便得到如图37(b)所示的两个互相垂直的节平面NP1和NP2及其极轴X和Y.NP1的方位角和倾角分别为φ1，δ1；NP2的方位角和倾角分别为φ2，δ2；极轴X的方位角和倾角分别为φx，δx；极轴Y的方位角和倾角分别为φy，δy.

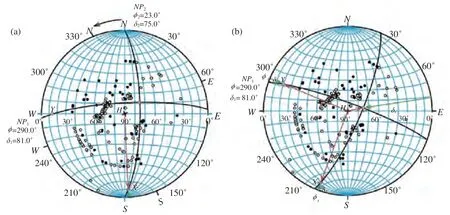
图37 确定与节面1（NP1）垂直的节面2（NP2）(a)将透明纸逆时针旋转φ2 角，画出方位角为φ2、倾角为δ2，过X 的弧线，即节面NP2；(b)将透明纸顺时针旋转φ2 角转回到原来位置Fig.37 To plot the second nodal plane 2 (NP2) perpendicular to the first nodal plane 1 (NP1)(a)Rotate anticlockwise the transparent paper at an angle of φ2,and draw an arc with an azimuth of φ2 and an dip of δ2 passing through the pole X,that is the second nodal plane NP2 perpencular to the flrst nodal plane NP1;(b)Rotate the transparent paper clockwise back φ2 to the original position

4.5 确定滑动角

如前已述，滑动角λ是断层上盘相对于下盘的运动方向（滑动方向）与断层走向的夹角，以顺时针为正，0°≤λ＜ 360°.如果节面2是断层面，那么极轴X（也可能是-X）是滑动方向；如果节面1 是断层面，那么极轴Y（也可能是-Y）是滑动方向.如果H点所在的象限是初动为“-”的象限，那么X轴与Y轴是滑动方向；如果H点所在的象限是初动为“+”的象限，那么-X轴与-Y轴是滑动方向.如图37(a)与图37(b)所示，要确定位于节面2 的极轴X或-X所代表的滑动角，只要将节面2 逆时针旋转φ2度[图37(a)]，使其走向正好与施密特网上的N极相重合，此时节面2 正好与表示倾角为δ2的子午线相重[图37(a)].从施密特网的N极起算，沿着该子午线从北向南（即顺时针）量出X轴与节面2 的走向的夹角λ′2，则λ2=360°-λ（′2如果H点所在的象限是初动为“－”的象限，则X轴是滑动方向）或λ2=180°-λ′2（如果H点所在的象限是初动为“+”的象限，则-X轴是滑动方向）.如果节面1 是断层面，用同一步骤，可以确定Y轴与节面1 的走向的夹角为λ′1，从而求出滑动角λ1=360°-λ（′1如果H点所在的象限是初动为“-”的象限、从而Y轴是滑动方向）或λ1=180°-λ（′1如果H点所在的象限是初动为“+”的象限，则-Y轴是滑动方向）.在图37 所示的例子中，因为H点所在的象限是初动为“-”的象限，所以-X轴与-Y轴是滑动方向.由上述步骤可以求得λ′2=171.0°，所以λ2=189.0°；λ′1=15.0°，所以λ1=345.0°.

4.6 确定应力轴

零轴（null axis，B轴）即节面1 与节面2 相交的轴线，在投影图上如图38(b)的B轴所示.压力轴（pressure axis，P轴）和张力轴（tension axis，T轴）位于XY平面（也即以B轴为极轴的赤道面）上并平分X轴与Y轴，P轴位于初动为膨胀（“-”或“○”）的象限，T轴位于初动为压缩（“+”或“●”）的象限.特别需要注意的是，P轴（压力轴）位于初动为膨胀（“+”或“○”）的象限，T轴（张力轴）位于初动为压缩（“+”或“●”）的象限，而不是相反.所谓压力轴（P轴）是指地震时释放的那部分应力（张量）的压应力轴，所谓初动为膨胀（“-”或“○”）是指发出的地震波初动表现为膨胀.所谓张力轴（T轴）是指地震时释放的那部分应力（张量）的张应力轴，实际上是最小主压应力轴.所谓初动为压缩（“+”或“●”）指所发出的地震波初动表现为压缩.为确定P轴和T轴，将透明纸逆时针旋转，使B落在施密特网上代表赤道面的直径WE的左半段WH上，此时X轴与Y轴便落在代表以B轴为极的赤道面的子午线[图38(a)中的虚线]上，P轴与T轴便是在该子午线上与X轴和Y轴成45°角的轴线的方向[图38(a)].现在顺时针旋转透明纸，使它回到原来位置[图38(b)]，便可得到断层面解.P轴，T轴以及B轴的方位角（azimuth）与倾角（plunge）(φP，δP)，(φT，δT)以及(φB，δB)，可以按照类似4.2 所述的、表示方位角为φ，离源角为ih的假想点的步骤读得.所不同的是，这些轴线的倾角指的是它们与水平面的夹角，而离源角ih则是离源射线与指向地心的地球半径方向（竖直方向）的夹角.以P轴为例，将透明纸逆时针旋转，使P轴落在NH上，此时，透明纸旋转的角度即φP，由在透明纸上量得的由施密特网上的水平面至P轴的角度即δp.

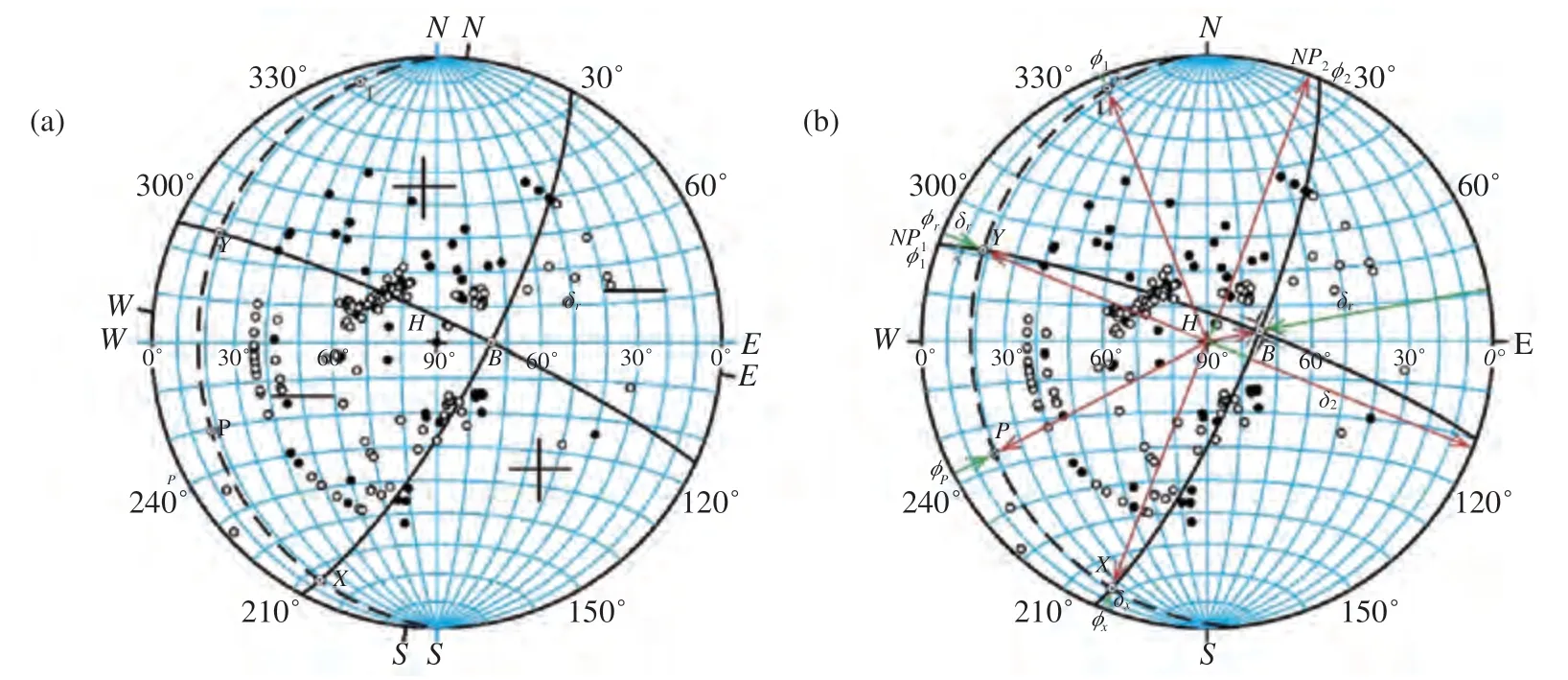
图38 确定应力轴(a) 将透明纸逆时针旋转使B 落在WH 上，画出P，T 轴；(b) 将透明纸转回原来位置得到断层面解Fig.38 To plot the stress axis(a)Rotate anticlockwise the transparent paper so that the pole B falls on WH and plot the P and T axes;(b)Turn clockwise the transparent paper back to the original position to get the fault plane solution

4.7 断层面解

按照上述步骤，便可得到如表3 所表示的地震的断层面解.以1975 年2 月4 日辽宁省海城MS7.3 地震为例，我们共收集到196 个国内外台站的P波初动资料，包括3 个台站的直达波数据、53 个台站的近震数据和140 个台站的远震数据（见附表1，附表2 和附表3）.根据这些数据得到该地震的断层面解（见表3 和图39），初动符号符合四象限分布的台站数为157 个，不符合四象限分布的矛盾台站数为39 个，根据公式（120）计算得到的矛盾比R为19.90%.图39 为以震源球等面积投影表示这次地震的断层面解，其中图39(a)为上半球投影，图39(b)为下半球投影.

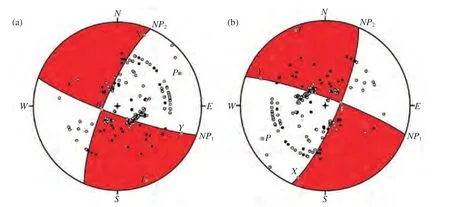
图39 1975 年2 月4 日辽宁省海城MS 7.3 地震的断层面解(a) 震源球上半球等面积投影；(b) 震源球下半球等面积投影Fig.39 Fault plane solution of the MS 7.3 earthquake in Haicheng,Liaoning Province on Feb.4,1975(a)Equal-area projection of the upper hemisphere of the focal sphere;(b)Equal-area projection of the lower hemisphere of the focal sphere

作为比较，图40(a)与图40(b)分别给出以震源球下半球与上半球极射赤面投影表示的海城MS7.3 地震的断层面解（顾浩鼎等，1976）.由图可见，同一个地震的断层面解，如果采用不同的震源球半球投影，那么由震源球上半球投影图旋转180°便可得到该地震断层面解的震源球下半球投影图；反之亦然.在运用如同表3 的表格表示断层面解时，节面1、节面2 的走向、倾角、滑动角的数值不变；主应力轴（P，B，T轴）的倾角数值也不变，但其方位角的数值则相差180°.原则上，节面1 与节面2 的命名是任意的.习惯上，常把真正的断层面（若能确认的话）称为节面1，另一个称为节面2.现在比较普遍的命名法是将走向角度小的节面称为节面1，走向大的节面称为节面2.

表3 1975 年2 月4 日辽宁省海城MS 7.3 地震的断层面解Table 3 Fault plane solution of MS 7.3 earthquake in Haicheng,Liaoning Province,Feb.4,1975

图40 1975 年2 月4 日辽宁省海城MS 7.3 地震的断层面解（顾浩鼎等，1976）(a) 震源球上半球极射赤面投影；(b) 震源球下半球极射赤面投影Fig.40 Fault plane solution of the MS 7.3 earthquake in Haicheng,Liaoning Province,Feb.4,1975 (Gu et al.,1975)(a)Stereographic projection of the upper hemisphere of the focal sphere；(b)Stereographic projection of the lower hemisphere of the focal sphere

致谢：中国地震局地球物理研究所孔韩东博士、李赞硕士，中国地震台网中心邹立晔高级工程师为本文图件的绘制，做了大量的工作，在此表示衷心感谢.

附录

附表1 1975 年2 月4 日辽宁海城MS 7.3 地震直达波数据Table 1 Direct wave data of Haicheng MS 7.3 earthquake on February 4,1975

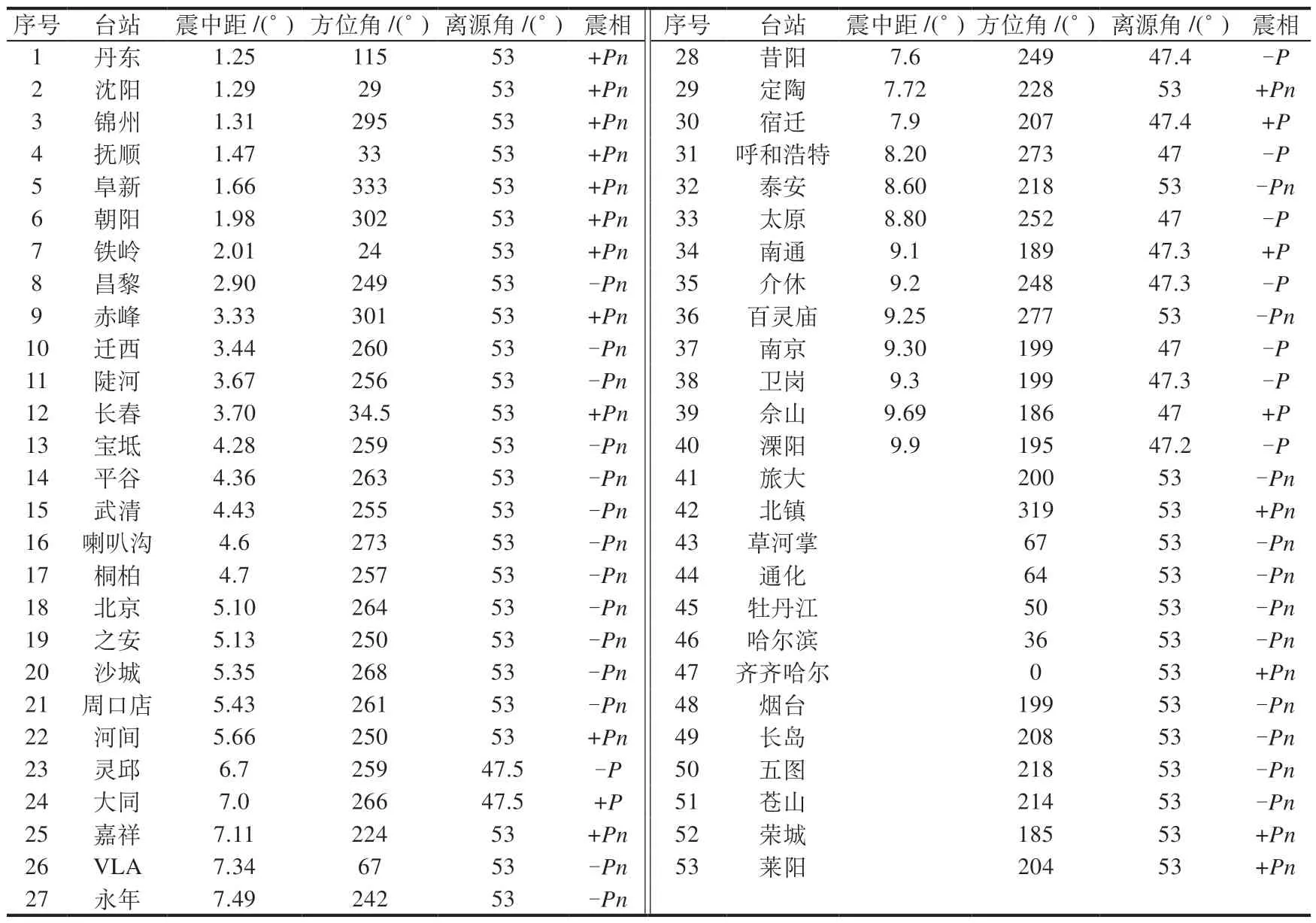
附表2 1975 年2 月4 日辽宁海城MS7.3 地震近震数据Table 2 Local earthquake data of MS7.3 earthquake in Haicheng,Liaoning Province,Feb.4,1975

附表3 1975 年2 月4 日辽宁海城MS 7.3 地震远震数据Table 3 Teleseismic data of Haicheng MS 7.3 earthquake on Feb.4,1975

续附表3