基于波谱分析方法的波速比计算软件

高 亮 汤曜炜 杨 选

（中国广州510070 广东省地震局）

0 引言

传统测定波速比的方法为和达法，有单台和达法和多台和达法。实际中较多采用多台和达法。多台和达法利用一组台站记录的地震事件的P 波走时tP和S 波与P 波走时差tS-P来测定波速比，该方法存在以下问题：①受时间精度的影响；②震相识别存在误差；③得到的波速比是各台站至震源传播路径的平均值，并非震源处的波速比；④受台站布局的影响，台站分布不均匀时得到的只是局部区域的波速比。

在对中强地震前后地震序列的研究中，地震学家发现波速比往往会呈现出“下降—恢复”的异常变化。孕震理论对以上现象解释为，在地震孕育过程中，特别是在其后期，孕震区内岩石的大量微裂隙会发生空间排列的变化，介质的孔隙度和各向异性程度等随之发生改变，以致地震波的传播速度受到影响。由于和达法求取波速比存在缺陷，部分学者倾向利用地震波波谱分析求取震源处的波速比。这种方法的优点是不受时间精度和震相识别误差的影响。在地震预报实践中，二者之间可以彼此印证，互相补充。目前国内外有不少学者进行过相关研究，均取得了较好的效果。许健生等（1998）对天祝—古浪5.4 级地震的研究表明，主震后地震的纵、横波位移谱零频极限的对数比值从1.2 左右下降到1.0 左右；张永久等（2004）通过纵、横波位移谱零频极限比值的计算，得到雅江6.0 级地震序列前后波速比的异常变化；陈丽娟等（2015）计算了纵横波位移谱零频极限比值与拐角频率比值，得到芦山MS7.0 地震序列前后波速比异常变化。利用拐角频率比与零频极限比值计算波速比的过程较为复杂，涉及地震仪器响应计算、纵横地震波谱分析、纵横波拐角频率与零频极限计算等。当前，研发一款使用方便、界面友好的软件以进行波谱分析下的波速比计算是有意义的。笔者在MATLAB 平台下，开发了一款利用纵横波拐角频率与位移谱零频极限值求解波速比的软件。本软件用于计算震源处的波速比，集成了上述计算功能，且具备绘图功能，在操作界面设有对应控件，界面友好，操作简便。

1 波速比求解理论

1.1 地震波形谱分析

要计算拐角频率、位移谱零频极限值，波谱分析是计算基础。波谱分析在软件中采用平移窗谱方法（Chael，1987）。首先，将选取的P、S波波形分成若干包含256个采样点的小段，并使相邻小段之间有50%的重叠。对于采样率为50 Hz 的地震记录来说，每个小段的时间长度是 5.1 s。然后，在每一小段波形的起始和末尾加5% COS 边瓣，通过快速傅里叶变换得到每个小段的傅里叶谱。最后，对每个小段的傅里叶谱进行仪器响应校正，并通过式（1）得到位移谱振幅a(f)。

其中，vi(f)是经过去仪器响应之后的第i小段傅里叶速度谱，f指傅里叶变换的各个频率点，T为选取P、S 波波形总持续时间，n为选取的P、S 波波形所拆分的小段数量，t为包含256 采样点小段时间长度，t=5.1 s。

对于噪声扣除，根据P 波初动前256 个采样点的噪声记录，通过式（2）可以计算归一到与信号相同持续时间的噪声位移谱振幅。

1.2 位移谱拐角频率与零频极限值理论计算方法

在频率域对地震波进行波谱分析，可得到拐角频率、位移谱零频极限值以及高频衰减斜率。对于中小地震，震源谱符合Brune 圆盘模型（Brune，1970），在忽略非弹性衰减的情况下，震源位移谱U(f)可表示为

其中，U0为位移谱零频极限值，f为频率，fc为拐角频率。当U0和fc确定时，即可得到理论震源位移谱。在实践中，需要根据已知地震记录位移谱来反演U0和fc。一般采用拟合法计算U0和fc（蔡杏辉，2015）。

根据式（4），在低频段（f1—f2），U(f)≈U0，则位移谱平方的积分为

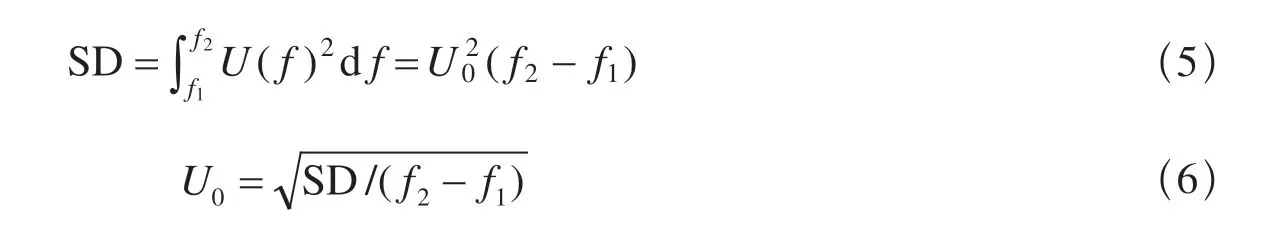
根据式（5）—（6），先在低频段（f1—f2）积分计算SD，进而求取U0。

1.3 纵横波波速比计算

1.3.1 利用纵横波拐角频率比值求解。圆盘面位错源产生的地震P 波和S 波远场位移的频谱可以表示为

其中，ρ是介质密度，m0是地震矩，α与β分别是P 波与S 波速度，R为震源距，ω为圆频率分别为P 波、S 波辐射图形因子，Fα(ω)与Fβ(ω)为纵横波频谱形状的函数，可以统一写作

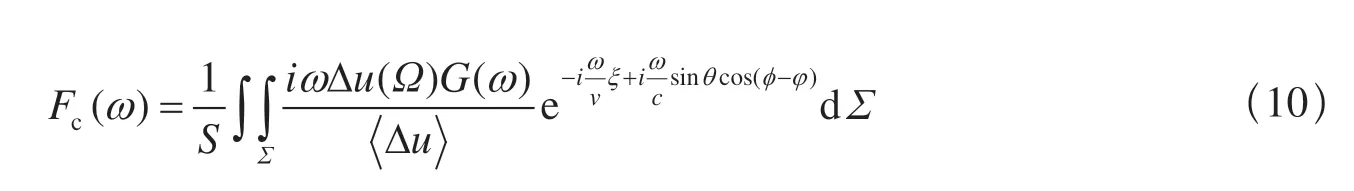
式中，c代表α或β，S为圆盘位错面积，为任意一点Ω的位错元dΣ的平面极坐标，Δu(Ω)表示位错元在圆盘位错面上的静力错距，是整个位错面上的平均值，G(ω)是震源时间函数G(t)的频谱，G(t)是阶跃函数，v表示圆盘中心向外破裂速度。陈运泰（1976）给出式（10）的积分结果，进而给出式（7）与式（8）的值，讨论了UP(ω)与US(ω)的高频和低频渐进行为，并给出2 条渐进线的交点所对应的拐角频率，则有

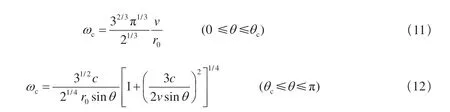
其中，θ为观测点在球极坐标系(r,θ,φ)的θ项，r0为圆盘形剪切面的破裂半径，当考虑破裂速度v无限大的情况时，可近似当作同时破裂情形处理，此时拐角频率的表达式可以为对于在震源球上随机分布的观测点，则地震拐角频率期望值可近似为

则由式（13）可得

由于ω=2πf，则利用纵横波拐角频率比值，可以计算得到震源处纵横波波速比。

1.3.2 利用纵横波位移谱零频极限比值求解。位移谱曲线在低频部分平坦，当ω→0 时，由式（7）—（8）推导得到纵横波零频极限值为

比较式（15）—（16）可以得到

由式（17）可知，纵横波波速比与纵横波零频极限比值及辐射图形因子有关，但对于同一序列、同一地区的地震，可以近似认为辐射图形因子比值为常数。计算中，辐射图形因子可取所有观测点辐射图形因子平均值，一般来说，P 波平均辐射图形因子为0.52，S 波平均辐射图形因子为0.63（Aki K et al，1980）。

2 软件计算流程

软件计算流程为：①导入原始地震编目文件；②导入地震台站仪器参数数据，计算仪器响应数据；③设置编目文件的相对工作目录，自动导入编目对应原始地震的各台波形文件；④批量计算P 波、S 波位移谱、拐角频率与零频极限值；⑤由拐角频率与零频极限值计算波速比；⑥循环计算完成某地震序列所有地震波速比后，绘制其空间与时间分布图。

2.1 数据导入

计算流程中有3 个基本数据需要导入，分别是地震编目数据、波形数据、台站仪器参数数据。以上数据均可以从JOPNES 地震速报分析系统中获取，地震编目数据是目前通用的.phase 数据，波形数据是JOPNES 地震速报分析系统截取导出的.sac 数据文件。.sac 数据格式广泛用于地震学分析软件，也是地震波形数据的通用格式有ASCII 码和二进制码2种格式，本软件数据导入采用.sac 二进制码格式。地震台站地震计参数也是JOPNES 地震速报分析系统导出的.ascII 文件中的.par 文件，包含对应地震记录的地震计灵敏度、传递函数零极点等信息。导入相关仪器参数信息后，可绘制仪器幅频响应图并直观显示，能在对地震波谱进行仪器响应校正之前判断仪器响应是否准确。

2.2 地震P 波、S 波位移谱求取

P、S 波的位移谱求取是计算拐角频率与零频极限值的基础，需要在软件中解决以下3个问题。

2.2.1 P、S 波时间长度的确定。P 波时间长度为P 波初动至S 波初动之间波形的时间段。S 波时间长度为从S 波开始到包含90% S 波能量的时间段。刘杰等（2003）通过回归分析1 900 条地震记录，得到S 波截取时间长度与Pg、Sg 波走时差为线性关系，并拟合出具体线性表达式。本软件采用刘杰等（2003）的结果。在软件中，通过波形显示界面拾取Pg、Sg 波走时差，确定S 波时间长度。

2.2.2 扣除仪器响应。通过仪器参数文件计算仪器的幅频响应，用地震记录速度谱除以各频点的仪器幅频响应。

2.2.3 去除背景噪声。选取Pg 波或Pn 波到时前256 个点的时间段波形，计算背景噪声位移谱，根据式（3），得到所需地震波位移谱。

2.3 波速比的计算

一个地震一般会被多个地震观测台站记录到，可以使用每个台站的波形资料分别计算拐角频率fc与零频极限值U0，再计算多台平均值，最后将平均拐角频率与平均零频极限值代入式（14）或式（17）算出波速比。为消除个别台站异常高值对平均值的影响，在计算平均值时采用式（18）—（19）。

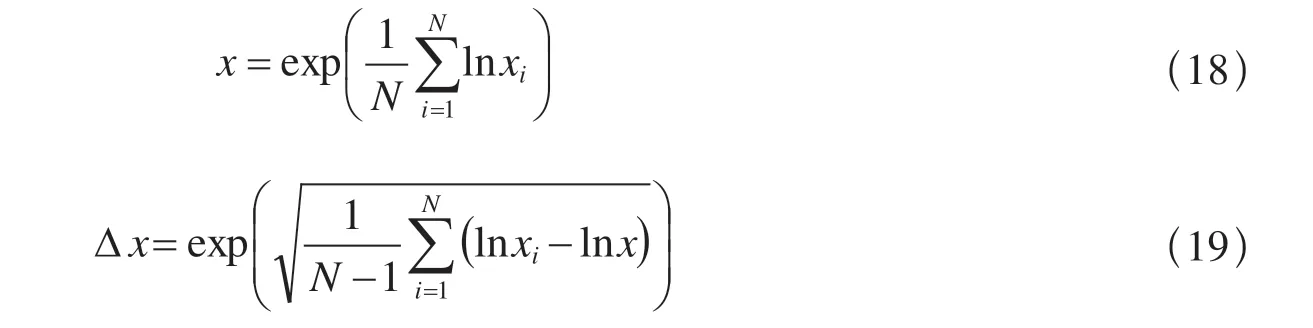
式中，xi为各台站的拐角频率fc或零频极限值U0，N为台站数。Δx为误差因子，其意义为当x以对数坐标作图时的标准差。

3 软件使用说明

3.1 软件界面

软件主界面（图1）包含基本参数输入、计算方法选择、结果显示。基本参数输入部分可导入地理底图、地震编目、仪器参数等。计算方法选择部分可以点选多台和达法或者波谱分析方法来计算波速比。结果显示部分将波速比结果用等值线绘制在界面中间地理底图上，正下方坐标图显示波速比随时间变化曲线。在导入各台仪器参数文件之后，软件界面右上角坐标图可以显示不同台站仪器幅频响应曲线。

图1 程序界面Fig.1 The graphic interface of the program

如图2 所示，在扣除仪器响应之前，可以观察地震计幅频响应曲线以避免错误。

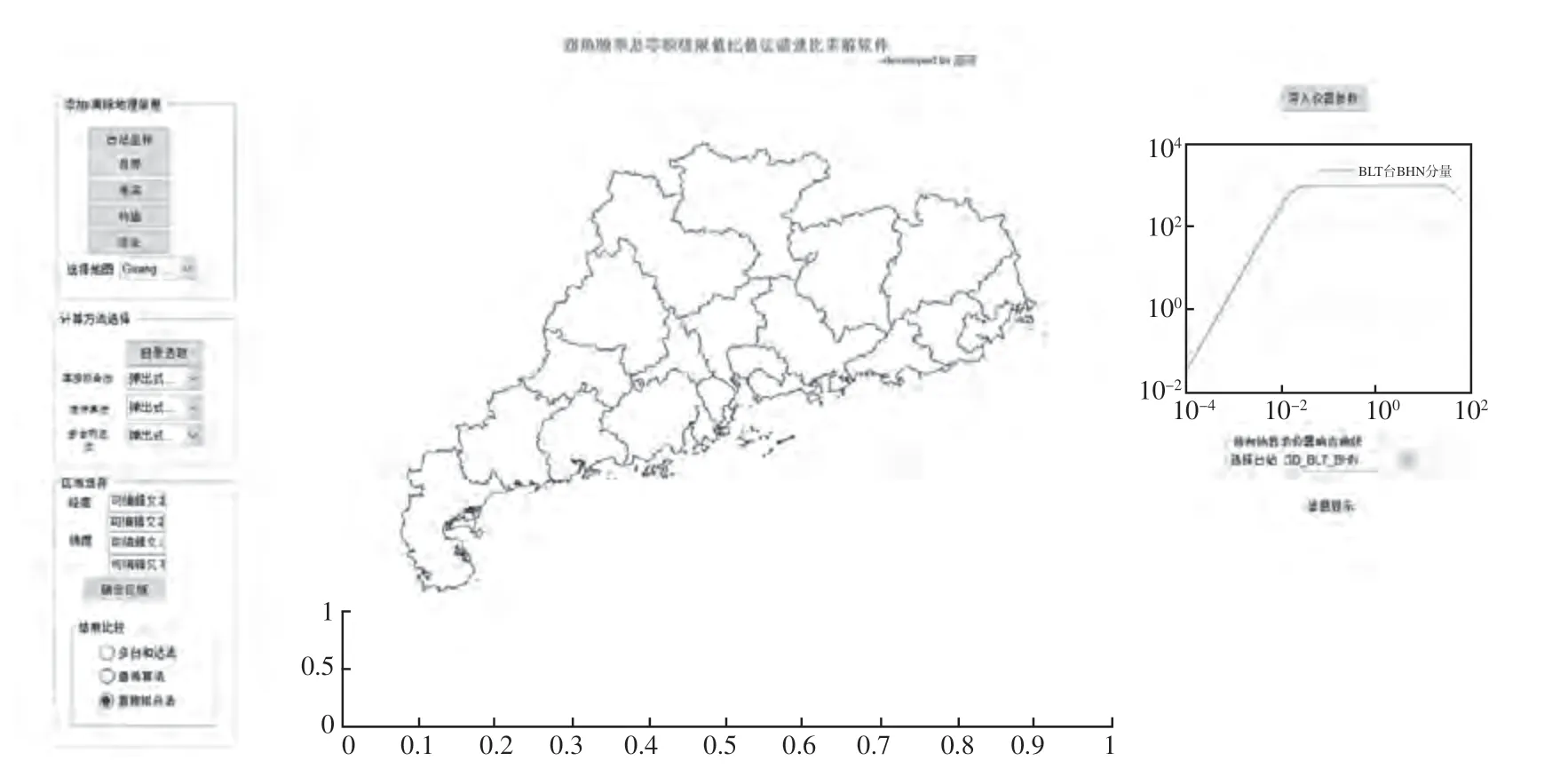
图2 地震计分量仪器响应曲线Fig.2 The amplitude frequency response curve of a seismograph

3.2 软件操作流程

首先，导入基础地理数据，例如研究区域的省级区域底图，图2 中显示的是广东省地理底图，还可以选择添加各类地理信息，如台站、县名、构造、河流等，这些地理要素需要事先打包在软件包里。然后，导入仪器参数，计算仪器响应。最后，导入地震编目数据.phase 文件及与地震编目对应观测台站原始波形记录.sac 文件。如图3 所示，数据导入完成后，软件界面中间显示震中分布，右侧表格显示地震目录相关信息。

图3 显示地震信息并绘制震中分布Fig.3 Show the seismic information and plot seismic distribution map

当选择某经纬度区域内的地震序列进行计算时，对于使用不同台站地震波原始记录计算的该地震序列的拐角频率值及零频极限值结果，软件会自动保存图像，如图4 所示。

图4 GD.201810281418 地震事件DNB 台地震记录拐角频率与零频极限值结果Fig.4 The corner frequency and zero spectrum limit value of GD.201810281418 earthquake at DNB station

在地震序列所中有地震的计算完成后，每个地震的拐角频率与零频极限值以表格形式显示。

4 实例分析

4.1 实例计算

以2018 年10 月至2020 年2 月广东阳江区域19 个ML2.0 以上地震为例，分别计算P 波、S 波拐角频率、零频极限值及对应波速比，计算结果在软件中弹出窗口以表格显示，如图5 所示。使用2 种方法计算的该序列波速比随时间变化曲线如图6 所示。

图5 地震序列P 波S 波拐角频率、零频极限值及对应波速比结果Fig.5 The P,S wave corner frequency,zero spectrum limit value,and relative wave velocity ratio result of the earthquake sequence

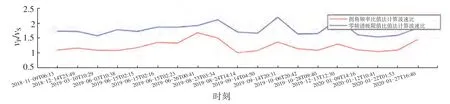
图6 拐角频率法波速比变化曲线与零频极限值比值法波速比变化曲线Fig.6 The wave velocity ratio curve by P,S wave corner frequency method,and zero spectrum limit value method

为了方便的比较2 种不同方法计算的波速比随时间变化趋势，可通过本软件将计算结果归一化于[0，1]区间内，如图7 所示。

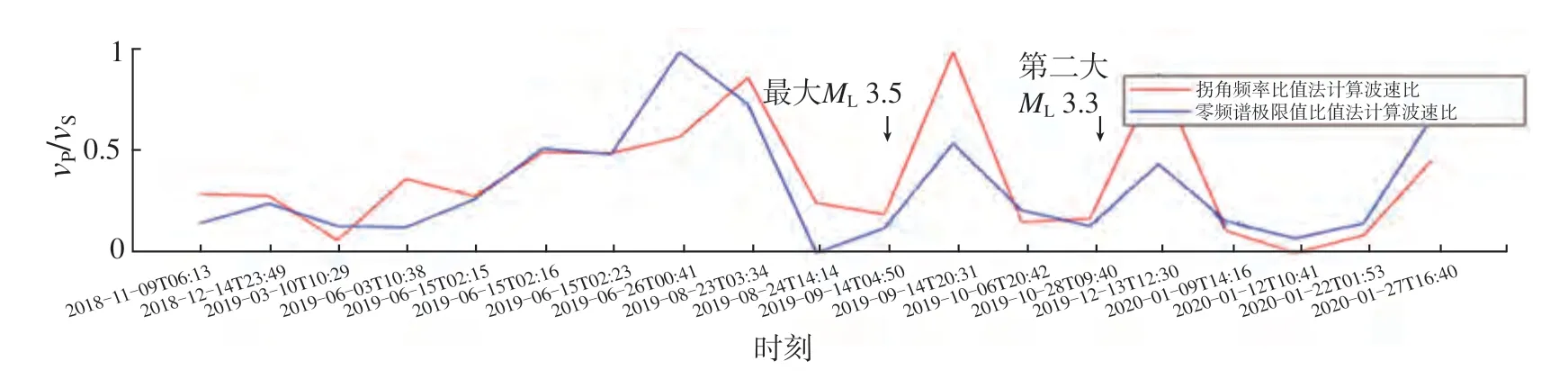
图7 归一化后2 种方法计算的波速比变化趋势对比曲线Fig.7 The comparative curves of the normalized velocity ratio by two methods

4.2 软件计算结果分析

陈丽娟等（2015）利用拐角频率比值法得到波速比平均值约1.27，零频极限比值法得到波速比平均值为1.67。由零频极限比值法所得波速比较拐角频率法更接近泊松比。本软件对上述地震序列19 例地震计算结果显示，利用拐角频率比值所得波速比平均值约为1.20，零频极限比值法所得波速比为1.767 6，与陈丽娟等（2015）的计算结果较为一致。且本软件用零频极限比值法所得波速比更接近泊松比数值1.73。对于2 种结果的差异，陈丽娟等（2015）解释为，在零频极限值与拐角频率值的反演过程中，对震源谱的低频水平段f1、f2和衰减段f3有个初始的预设限定，若预初始值不恰当，可能会造成某些地震记录拐角频率计算误差较大，而零频极限值受初始值影响相对较小。另外，拐角频率与破裂过程有关，且随台站与断层面之间的夹角变化，而零频极限值与频率、破裂过程无关，所以零频极限比值法计算结果更为稳定。

由图7 可见，零频极限比值法与拐角频率比值法所得波速比曲线随时间的变化趋势有较好的一致性。为了检查2 种结果之间的相关性，利用MATLAB 中自带corrcoef 函数，计算得到零频极限比值法与拐角频率比值法的相关系数，数值为0.73，可以认为，2 种结果具有较强的相关性，2 种不同波谱分析计算方法能够相互印证。

中强地震前地震波速比值出现异常。诸多研究表明，地震前纵横波速比表现为“下降—恢复”的异常形态。由本软件计算结果图可见，特别是在整个地震序列最大地震ML3.5 地震前和第二大地震ML3.3 地震前，波速比表现出“下降—恢复”的异常变化，与前人所得结果一致。

5 结束语

通过地震波谱分析求取震源处的波速比，其优点是不受时间精度和震相识别误差的影响。在地震预报实践中，可以与常用的多台和达法互相补充。笔者以MATLAB 为开发平台，编制了基于P、S 波拐角频率与零频极限值比值的波速比计算软件，将导入波形数据、去仪器响应、求取位移谱、计算拐角频率与零频极限值、结果可视化及比较集成一体，可用于某个区域范围内波速比计算、大震序列前后震源区波速比追踪、判断未来地震序列发展趋势、判别大震之后强余震的发生等工作。在实际应用中，为了保证拐角频率与零频极限值的计算准确性，需要对研究区域的地震序列位移谱水平段f1、f2和衰减段f3做预先判定，设置较恰当的初始值，以期获得较好的反演结果。

该软件使得繁琐的频谱计算过程简化，且界面友好，操作简单，便于推广使用。