基于FPGA的高压直流输电系统建模与实时仿真

黄冠标，翟鹤峰，赵利刚，洪 潮

（直流输电技术国家重点实验室（南方电网科学研究院有限责任公司），广州 510663）

高压直流输电技术的不断发展与广泛应用使得输电网呈现出明显的多区域交直流互联的特点，其结构与运行特性发生了深刻变化[1−2]。输电网中接入了大量电力电子设备，与传统输电网相比其动态特性更加复杂，时间尺度更小，必须依靠有效的仿真方法与工具研究系统动态特征。实时仿真采用详细的数学模型与微秒级的仿真步长进行瞬时值仿真，能够准确“再现”系统的运行状态，分析系统的动态特性，并对实际物理设备进行在线测试[3]。然而对大规模电力电子元件[4]复杂动态特性的精准“复现”依托于高效的计算方法与可靠的硬件平台，这是实现高压直流输电系统实时仿真的重要保证。

近年来，国内外学者对高压直流输电系统实时仿真进行了大量的研究。文献[5]基于中央处理器CPU（central processing unit）构建了直流系统的实时仿真模型，并与真实物理直流装置连接，实现了硬件在环HIL（hardware−in−the−loop）仿真；文献[6]基于HYPERSIM提出了优化解耦和子任务映射方法，对直流输电系统进行数模混合仿真建模，并实现了50 μs仿真步长下直流系统的实时仿真；文献[7]在全数字实时仿真装置ADPSS中实现了高压直流输电系统的机电−电磁混合仿真；文献[8]针对高压直流输电系统中的换流器模型、输电线路模型等进行数学建模，并在数字实时仿真器RTDS中完成了高压直流输电系统仿真测试；文献[9]设计了基于SSN解算器的高压直流输电系统仿真模型，并在RT−LAB中实现了该系统的实时仿真。

尽管对于HVDC系统的实时仿真研究已取得了一定进展，但开发步长更小、精度更高、规模更大的HVDC实时仿真系统仍然面临以下困难：大量电力电子元件具有高频开关特性，对该类元件的仿真需要较小的仿真步长；而大量电力电子元件的详细建模则加大了仿真规模，且其控制策略十分复杂，对控制器的仿真需要较大的仿真步长[10]。因此解决多电力电子的高压直流输电系统仿真步长与仿真规模的冲突，满足实时分析需求，是高压直流输电系统实时仿真亟待解决的关键问题。FPGA采用分布式存储结构，具有计算速度快等优势，满足小步长实时仿真的需求，在实时仿真器的研究与开发中表现出巨大的潜力[11]。

本文选用FPGA作为底层计算硬件，提出了高压直流系统中各元件的详细建模方法，设计了基于FPGA的元件模块，完成了基于FPGA的高压直流输电系统的建模，并在平台中搭建了CIGRE标准算例与PSCAD/EMTDC仿真结果对比，验证了所设计的基于FPGA的HVDC实时仿真系统的高速性和有效性。

1 HVDC实时仿真方法

本文以文献[12]为参考，将整个高压直流输电系统划分为电气与控制系统独立求解，其中：电气系统采用节点分析法，控制系统采用顺序求解法，二者并行计算，并进行实时数据交互。

1.1 HVDC拓扑结构

高压直流输电系统按照换流站的换流方式可分为电网换相换流器高压直流输电LCC−HVDC（line commutated converter based high voltage direct current）以及电压源换流器型高压直流输电VSC−HVDC（voltage source converter based high voltage direct current）[13]。以LCC−HVDC为例介绍高压直流输电系统的拓扑结构，如图1所示。

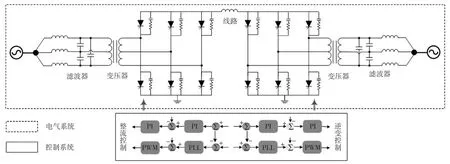
图1 LCC-HVDC拓扑结构Fig.1 LCC-HVDC topology

LCC−HVDC为单极接地系统，其电气系统主要包括滤波器、换流变压器、换流站以及直流线路等。滤波器由RLC元件串并联组成，用来消除经整流或逆变后的高次谐波和低次谐波；换流站由晶闸管换流桥臂组成，根据其个数可以分为6脉波、12脉波等形式；换流变压器为三相双绕组变压器。控制系统可分为整流器和逆变器的控制两部分，电气系统与控制系统之间交互电压电流以及晶闸管的开通信号。

1.2 实时仿真方法

在实时仿真中，HVDC系统的电气元件由伏安特性方程描述，需对整个系统联立求解；而控制元件由输入输出关系描述，需对各元件依次求解。

1）电气系统求解方法

电气系统采用节点法进行求解，其求解流程分为3步，以图2所示的电容支路及其暂态计算电路为例具体说明。

图2 电容支路及其暂态计算电路Fig.2 Capacitance branch and its transient calculation circuit

步骤1列出电容元件的伏安特性方程，有

式中：ikm(t)为电容支路流过的电流；vk(t)和vm(t)分别为电容两端的电压；C为电容。采用梯形积分法差分，得到差分方程为

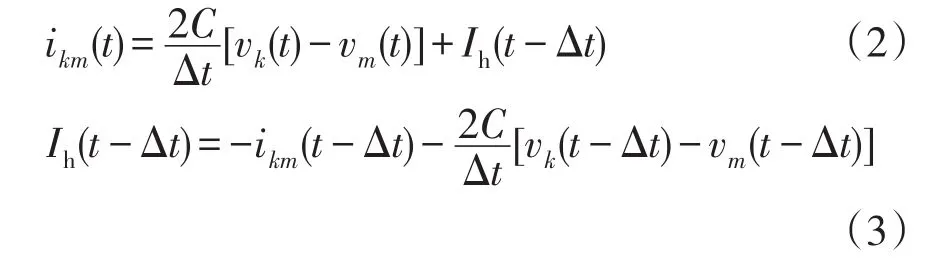
式中：Ih(t−Δt)为历史项电流源的值；vk(t−Δt)和vm(t−Δt)分别为上一时步的电容两端电压；Δt为仿真步长。式（2）可以看作一个历史相电流源和一个等效计算电导并联形式的等效电路的方程描述。

步骤2联立所有电气元件的差分方程，得到整个系统的节点方程，通过求解式（3）的线性方程组得到各节点的电压瞬时值。

式中：G为系统的导纳矩阵；u为系统节点电压向量；i为系统支路电流向量。

步骤3通过求解的各节点电压更新支路电压和支路电流，并作为下一时步的初值。

2）控制系统求解方法

控制系统中存在较多的非线性元件，求解规模大，为保证微妙级实时仿真，本文采取顺序求解方法对控制系统进行求解，对于控制电路中的反馈环节，插入一个步长延迟进行处理。

2 基于FPGA的HVDC系统建模

为保证小步长下实时仿真的精度，需要对HVDC系统的各元件建立详细模型。以HVDC系统中重要的晶闸管、变压器元件以及控制系统的核心环节为例，说明基于FPGA的实时仿真建模方法。

2.1 HVDC电气系统

1）晶闸管建模

对于电力电子变流装置建模方法通常分为拓扑建模法和输出建模法[14−15]，为了描述其内部详细的电气信息，需要采用拓扑建模法的详细模型对HVDC系统中的晶闸管模型建模，本文使用ADC法[16]对晶闸管进行建模。该方法可以保证开关状态切换时系统节点导纳矩阵保持不变，具体方法为：晶闸管导通时等效为小电感，晶闸管未导通时等效为小电阻和小电容的串联。采用梯形差分法的晶闸管的特性方程为

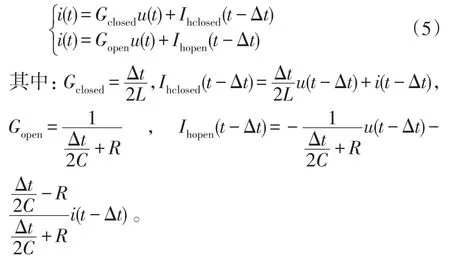
式中：Gclosed和Gopen分别为晶闸管闭合和断开时的导纳；Ihclosed(t−Δt)和Ihopen(t−Δt)分别为晶闸管闭合和断开时历史项电流源的值；R、L和C分别为等效的电阻、电感和电容；u(t−Δt)和i(t−Δt)分别为上一时步晶闸管两端电压和流过晶闸管的电流。

将历史项电流源表达式写为通用表达式，则有

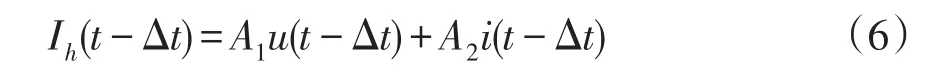
式中，A1和A2为晶闸管闭合和断开状态的系数。

基于FPGA的晶闸管模块设计如图3所示。图3中，RAMcon_sig、RAMstate、RAMV、RAMI、RAMhist分别存储晶闸管的控制信号、每时步的状态、电压、电流以及历史量。在每一时步的开始信号到来后，分别从相应的RAM中读取出控制信号controlsig、晶闸管上一时步状态statehist、开关电压V以及开关电流I，开关电压V经过与导通阈值比较后得到晶闸管导通允许信号Vclose，与控制信号controlsig以及晶闸管上一时步状态statehist共同判断晶闸管是否能够导通（导通条件为有导通信号且两端电压大于导通阈值电压），得到本时步晶闸管状态state，并与从RAM中读出的电压V和电流I求解历史项电流源histw，将其转化为整个系统的历史量Iaug输出；同时，将其写入RAMhist中待第3步更新时使用。当第2步求解完方程组后，第3步更新阶段开始，从ROMG中读出预存的导纳逆矩阵，求解该时步的节点电压V和支路电流I，同时支路电流I用来判断晶闸管是否关断（若支路电流小于维持电流，则晶闸管关断；否则维持导通），并将晶闸管状态存入RAMstate待下一时步求解，如此完成晶闸管一个时步求解的全过程。其历史量求解模块和更新计算子模块的FPGA设计分别如图4和图5所示。

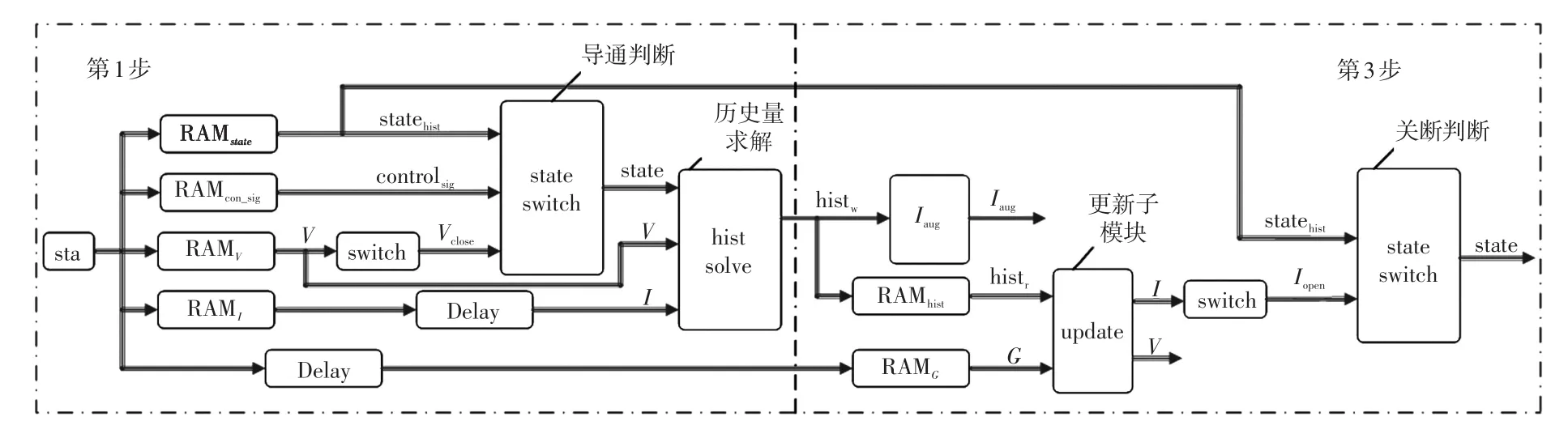
图3 基于FPGA的晶闸管模块设计Fig.3 Design of thyristor module based on FPGA

图4 历史量求解模块设计Fig.4 Design of solving module for historical quantity

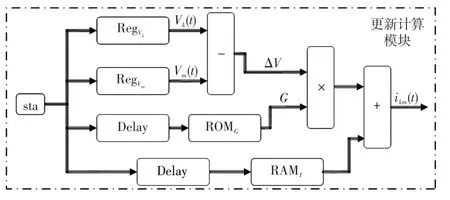
图5 更新计算模块设计Fig.5 Design of update calculation module

2）换流变压器建模

换流变压器是连接换流桥与交流系统的电力变压器，为换流桥提供一个中性点不接地的三相换相电压，实现交直流系统的电气隔离，换流变压器与换流桥是构成换流单元的主体。本文针对HVDC系统中的换流变压器模型，设计了变压器更新模块，如图6所示。

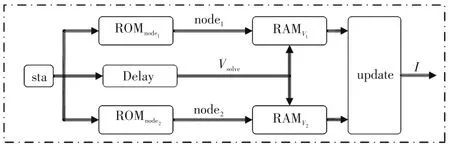
图6 基于FPGA的变压器模块设计Fig.6 Design of transformer module based on FPGA

变压器并不会形成历史项电流，因此只在更新模块更新支路电流值并输出，当开始信号到来后，分别从ROMnode1、ROMnode2中读出一次侧和二次侧的节点编号，并与求解得到的节点电压一同进行更新支路电流I并输出。

2.2 HVDC控制系统

1）传递函数

在HVDC系统中，一阶传递函数是最为常见的，如PI控制环节、超前滞后环节、积分环节等，这里以一阶传递函数为例说明其基于FPGA的设计方式。一阶传递函数的通用表达式为

式中：Y为输出信号；X输入信号。将式（7）写作微分方程，有

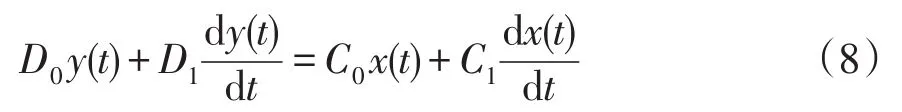
对式（8）使用梯形法，可得差分方程为

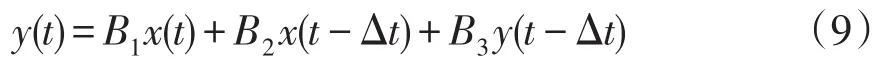
其FPGA设计如图7所示。该模块可以通过3个乘法单元和2个加法单元实现。3个寄存器分别存储B1、B2与B3，并分别与输入值x(t)、上一时步的输入值x(t−Δt)以及上一步长的输出值y(t−Δt)相乘；3个乘法器并行执行，将其结果依次相加得到输出值y(t)，同时将该时步的输如x(t)及输出y(t)存入相应寄存器，以便下一时步求解。

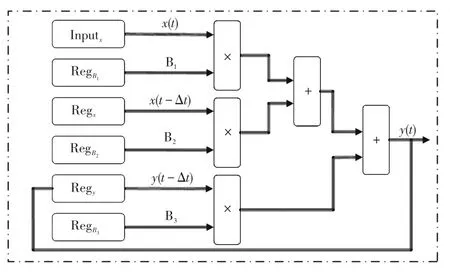
图7 基于FPGA的传递函数求解模块设计Fig.7 Design of solving module for transfer function based on FPGA

2）正弦求解模块

在控制系统如锁相环PLL和逆变侧的熄弧角控制环节中等，需要用到大量的正弦求解模块。正弦求解模块在FPGA中需要占用大量的逻辑资源，若对每个变量都单独使用一个正弦求解模块会造成资源的大量浪费，因此采用流水线的形式对正弦模块的求解进行设计，其FPGA设计如图8所示。

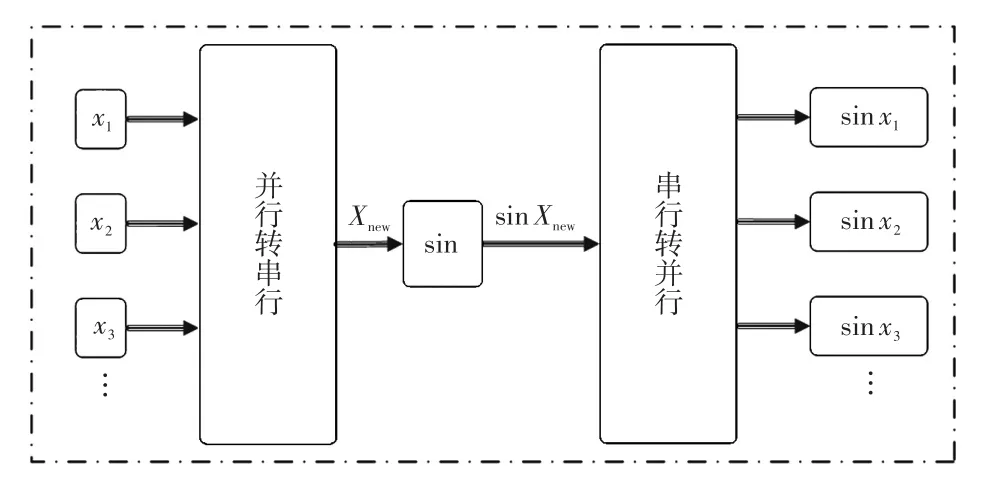
图8 基于FPGA的正弦求解模块设计Fig.8 Design of sine solving module based on FPGA

对于多个并行输入x1、x2、x3等，通过并行转串行接口，将其存放在同一寄存器中，寄存器的地址段由低到高依次存放x1、x2、x3，形成Xnew。依次选取对应地址段中的数据进行正弦计算，每个数据间隔一个时钟周期，当最后一个数据完成计算后再经串行转并行接口得到计算输出sinx1、sinx2、sinx3。当有N个并行数据同时计算时，该方法输出结果比并行计算多使用了（N−1）个时钟周期，但却节省了（N−1）个正弦模块，在满足步长要求的情况下减少了逻辑资源的使用。

（3）熄弧角检测模块

在直流输电系统中为了防止换相失败，需要维持熄弧角γ为给定值以保证晶闸管在关断后不会由于其高电位而重新导通，可以通过调节逆变器侧的超前触发角β进行控制[17]，基本原理如图9所示。

图9 定熄弧角控制原理Fig.9 Control principle for γ

图9中熄弧角的测量值对于该控制器的精确性有很大影响，本文中针对FPGA的并行特性设计了如图10所示的熄弧角检测模块。

图10 基于FPGA的熄弧角检测模块设计Fig.10 Design of detection module for γ based on FPGA

图中RegI、RegV分别存放上一时步的晶闸管电流和电压，与本时步的电流和电压值经过零检测后输出二者由正变负的时刻T1、T2，过零检测为锁存器，当检测到电压或电流上一时步为正数且本时步为负数时，时间信号Time可以输出，以此记录过零时刻。T1、T2的差值ΔT经过与2πf相乘转变为电角度γ输出。

3 算例分析

3.1 仿真算例

本文选取CIGRE的标准HVDC算例作为测试系统，将FPGA仿真结果与离线软件PSCAD/EMT⁃DC进行比较，以验证本文设计的正确性。

CIGRE HVDC系统的拓扑结构如图11所示，算例是一个单极500 kV、1 000 MW的高压直流输电系统，其整流侧和逆变器侧各经12脉波换流器与弱交流系统（额定频率为50 Hz，短路比为2.5）相连，系统两侧设置有阻尼滤波装置和电容无功补偿设备。控制策略整流侧采用恒电流控制，逆变侧采用恒电流控制、低压限流控制以及熄弧角控制。

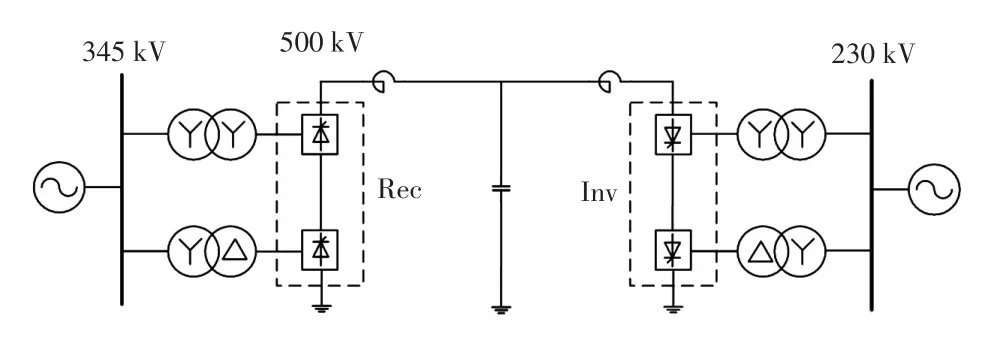
图11 CIGRE HVDC系统拓扑结构Fig.11 Topology of CIGRE HVDC system

实时仿真平台如图12所示[18]，FPGA实时仿真器通过125 MHz的时钟驱动，通过通用串行总线与上位机进行数据交互，为了满足仿真精度，采用两种基本数制，电气系统仿真采用了64位双精度浮点数与定点数数制，控制系统仿真采用32位单精度浮点数。

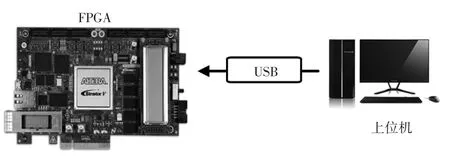
图12 FPGA实时仿真平台Fig.12 FPGA real-time simulation platform

HVDC系统的规模如下：系统导纳矩阵的维度为104，电源类元件6个、RLC元件94个、晶闸管元件24个、测量元件23个、线路元件1个以及换流变压器元件4个。其逻辑资源利用率为87%，专用乘法器利用率为25%，存储资源利用率为23%。在解算时间上，电气系统为3.76 μs，控制系统为4.32 μs，由于控制系统的求解与电气系统求解过程是并行的，因此实际解算时间取控制系统求解时间与电气系统求解时间的最大值，为保证仿真的实时性，整个系统采用5 μs的仿真步长。

3.2 单相接地故障

对故障进行详细动态仿真，从而对接入系统的实际保护装置进行测试是实时仿真的重要应用。在本算例中，设置0.6 s时HVDC系统逆变侧交流母线A相发生单相接地故障，0.1 s后故障切除。为了验证仿真结果的准确性，将CIGRE HVDC系统与PSCAD/EMTDC中的标准算例进行对比，对比结果如图13所示。

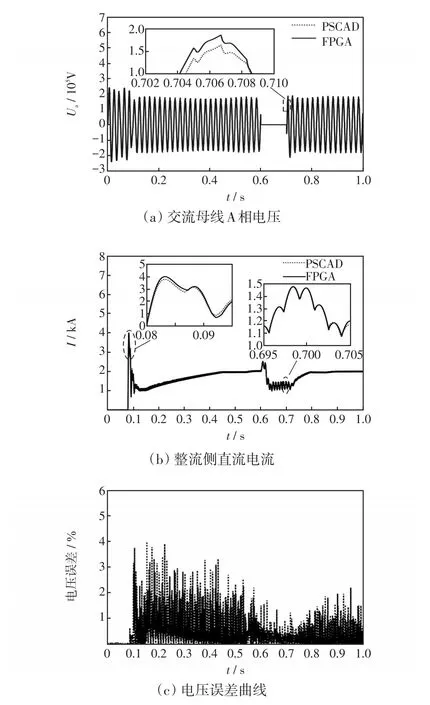
图13 仿真结果Fig.13 Simulation results

从图中可知，FPGA实时仿真器的输出结果与PSCAD/EMTDC离线仿真结果基本一致，发生故障后故障切除恢复的暂态特性都保持高度一致，仿真误差在5%以内，从而验证了基于FPGA实时仿真器的有效性和准确性。

4 结语

基于FPGA的HVDC实时仿真器对系统进行详细建模，以更小的步长、更快的速度、更高的精度满足实时仿真的需求，具有良好的发展前景。本文提出并设计了基于FPGA的HVDC实时仿真系统，针对HVDC系统的核心元件晶闸管、换流变压器等进行了详细建模与设计，并进一步针对控制系统的关键结构进行了设计，通过仿真搭建了CIGRE HVDC标准算例，验证了基于FPGA实时仿真器的数值精度和平台正确性。可为针对VSC−HVDC系统的实时仿真奠定基础，可以提高HVDC系统的仿真规模，增强基于FPGA的实时仿真器的通用性。