考虑机组组合和网络结构优化的电网规划方法

王伟臣，张天宇，宣文博，李 慧，刘忠义，王 魁

（1.国网天津市电力公司，天津 300010；2.国网天津市电力公司经济技术研究院，天津 300171）

能源危机与环境污染是21世纪人类社会面临的共同挑战。为了实现社会的可持续化发展，可再生能源的开发和利用在世界范围内受到越来越高的关注。与火电、水电等传统发电相比，风力发电等可再生能源发电的出力受天气、地理环境等复杂因素的影响，具有显著的间歇性、多变性与不确定性特征。随着风电接入规模的不断增加，电网运行方式更加多变，潮流分布特性更为复杂，面临的不确定性因素显著增加，对电网的安全性带来了严峻挑战，也将对电力系统的规划造成深远影响[1−2]。

输电网规划是电力系统规划的重要组成部分。电网规划的基本任务为：对于给定的未来规划年的负荷水平与发电资源，在现有网架结构的基础上，确定新建线路的位置、容量和时间等因素，以满足未来电网的负荷需求以及系统的安全性与可靠性的要求[3]。电网规划工作中，需要解决的一些基本问题包括：如何评价一个电网规划方案的有效性，如何考虑电网的各类约束条件，如何有效处理电网规划面临的各种不确定性因素等。从规划目标的方面，电网规划中考虑的目标函数主要包括投资成本最小、运行成本最小和可靠性损失最小等等。

为了有效应对风电接入的影响，要求电力系统具备足够的灵活性。一方面，电源要具备足够的调节能力以保证系统实时功率平衡；另一方面，电网的拓扑结构应该足够灵活以适应电网运行方式的复杂多变。在电源的灵活性方面，机组组合UC（unit commitment）问题是电力系统优化运行的重要组成部分[4]。合理的机组组合规划不仅有利于平衡实时变化的电力系统负荷，提高系统供电的可靠性，而且可以指导电力部门根据负荷预测数据合理投入和退出机组，分配各机组的出力，从而降低系统的发电成本。针对机组组合问题，已有学者在模型方面和求解算法方面开展了专门的研究。在模型方面，为了处理不确定性因素，主要方法包括基于多场景的机组组合方法[5−6]、基于鲁棒优化的机组组合方法[7−8]和基于机会约束的机组组合方法[9−10]等。文献[6]提出了一种改进的基于场景的随机规划方法以考虑能源市场汇总风电的不确定性；文献[7]提出了一种利用区间数来考虑负荷和风电不确定性的安全约束机组组合问题的鲁棒求解方法；文献[9]针对日前调度问题，考虑了系统负荷和可变再生能源的小时预报误差以及系统部件的随机故障，提出了基于机会约束的日前随机调度模型。机组组合问题实际上是包含0−1变量和连续变量的大型混合整数规划问题，在求解算法方面，传统优化算法如优先顺序法[11]、Benders分解法[12]，智能优化算法如遗传算法[13]、粒子群算法[14]等均被应用到机组组合问题的求解中。

在电网拓扑结构的灵活性方面，输电网结构优化OTS（optimal transmission switching）通过改变输电线路的开断状态，灵活改变网络的拓扑，从而改变系统的潮流分布与运行特性等，对于降低系统的损耗，提升系统的运行经济性，消除网络阻塞与电压越限，改善系统短路水平等方面具有显著作用。在电网规划中，考虑输电网结构优化是增加系统网络结构灵活性的重要手段，对于改善电网接纳可再生能源、改善系统的安全经济运行水平等具有重要意义。目前，国内外学者围绕输电网结构优化开展了较广泛的研究。文献[15]基于机会约束规划理论，建立了考虑风电利用率机会约束的输电网结构优化模型，通过合理改变电网的拓扑结构，改善风电消纳能力与发电成本；文献[16]建立了同时考虑输电网结构优化和线路动态增容的电网扩展规划模型；文献[17]以IEEE118节点系统为例，分析了输电网结构优化对系统运行成本的影响，结果表明，采用输电网结构优化后，可以有效降低系统的发电成本；文献[18]将考虑输电网结构优化的线路容量扩展规划问题建立为两阶段随机混合整数规划问题，并证明在大规模风电阻塞网络中采用输电网结构优化可以降低发电成本，提升最优线路扩容方案的经济性；文献[19]研究了开断部分线路对系统稳定性的影响，采用迭代的方法得到在交流潮流框架下可行的线路开断方案；文献[20]从输电网结构优化中面临的不确定因素入手，提出了以降低输电阻塞为目标的输电网结构优化数学模型，给出了考虑N−1安全网络约束的结构优化模型；文献[21]通过构造与原电网相似拓扑、不同参数的伴随网络，实现了输电网结构优化问题中线路开断与短路电流约束之间的显式线性关系表达，避免了线性化过程带来的误差问题以及非线性约束求解困难的问题。

如何在电网规划工作中，特别是含可再生能源电力系统的电网规划中，同时嵌入机组组合和输电网结构优化，以改善输电网规划工作的精细化和科学性是亟需解决的关键问题之一。而在目前的电网规划相关研究中尚未考虑此问题。本文针对目前研究中尚缺乏在含可再生能源电网规划中同时考虑机组组合和网络结构化的问题，建立了嵌入机组组合和网络结构优化的可再生能源接入系统的电网规划模型，借助机组组合和网络结构优化，系统分析电网规划方案的经济性和对未来规划年运行场景的适应性。

1 模型建立

本文提出的嵌入机组组合和输电网结构优化的含可再生能源电力系统规划方法的框架如图1所示。主要流程如下：

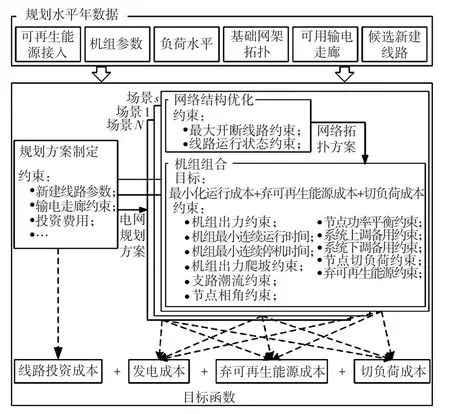
图1 方法框架Fig.1 Framework of the proposed method

（1）给定电网规划水平年数据，包括可再生能源接入、机组参数、负荷水平、基础网架拓扑、可用输电走廊和候选新建线路集合等；

（2）考虑输电走廊约束、新建线路参数、投资费用等条件，生成某一电网规划方案，即新建线路方案；

（3）对于生成的电网规划方案，针对可再生能源出力场景和负荷水平，考虑最大开断线路约束、线路运行状态约束等，进行网络结构优化，确定系统的网络拓扑结构，进而考虑机组的运行约束、系统潮流约束、旋转备用约束等，以运行成本、弃可再生能源成本和切负荷成本之和最小为优化目标，进行机组组合优化，对未来规划水平年典型场景s下进行运行模拟，评估电网规划方案。

1.1 目标函数

1.2 约束条件

式中，os,k,t为场景s下机组k在t时段的运行状态，1表示开机运行，0表示停机。即通过约束式（10）和式（11）共同限制机组的开机标志，以在系统运行成本中考虑机组的启动成本。

当os,k,t=1且os,k,t−1=0时，即若在运行场景s中，第k台机组在第t时段开机时，则式（10）变为hs,k,t≥ 1，考虑到hs,k,t为0−1变量，因此hs,k,t取值为1；当os,k,t=os,k,t−1=0 或os,k,t=os,k,t−1=1 ，即在运行场景s中第k台机组在第t时段的运行状态未发生变化时，式（10）变为hs,k,t≥0，即该约束不起作用；当os,k,t=0 且os,k,t−1=1时，式（10）变为hs,k,t≥ −1，即该约束不起作用。

当os,k,t=1且os,k,t−1=0时，即若在运行场景s中，第k台机组在第t时段开机时，则式（11）变为hs,k,t≤ 1，即该约束不起作用；当os,k,t=os,k,t−1=0 或os,k,t=os,k,t−1=1时，即在运行场景s中，第k台机组在第t时段的运行状态未发生变化时，式（11）变为hs,k,t≤ 0.5，考虑到hs,k,t为0−1变量，因此hs,k,t取值为0；当os,k,t=0 且os,k,t−1=1时，式（11）变为hs,k,t≤ 0，考虑到hs,k,t为0−1变量，因此hs,k,t取值为0。

如上所示，hs,k,t、os,k,t和os,k,t−1均为 0−1变量。由式（10）和式（11）可得在运行场景s中，若第k台机组在第t时段开机，则hs,k,t=1；否则，hs,k,t=0。

最小开机时间约束和最小停机时间约束即考虑到机组设备的损耗和运行要求，一般机组一旦开机至少需要运行一定时间才能停机，反之亦然。分别表示为

参考节点的相角约束即系统中的平衡节点的电压相角θref,s,t为0，表示为

切负荷约束即每个节点允许切除的负荷需要在0到节点负荷预测值范围之内，表示为

弃可再生能源约束，即每个风电场的弃可再生能源发电功率需要介于0到其出力预测范围之内，表示为

如前所述，本文所建立的模型为一个二次规划模型，即目标函数包含决策变量的二次项，并且约束条件均为决策变量的线性约束。Gurobi、Cplex等商业求解器对此类问题的求解具有良好效果。因此，本文采用Gurobi求解器[22]对上述所建立的二次规划模型进行求解。

2 算例分析

本节以IEEE RTS−24算例系统为例，对所建立的嵌入机组组合和输电网结构优化的可再生能源并网系统规划模型的有效性与合理性进行验证。

IEEE RTS−24系统的接线如图2所示，系统包含24个节点、33条线路。5台变压器分别位于线路L3−24、L9−11、L9−12、L10−11和L10−12，将系统分为低压区138 kV和高压区230 kV两个电压等级。

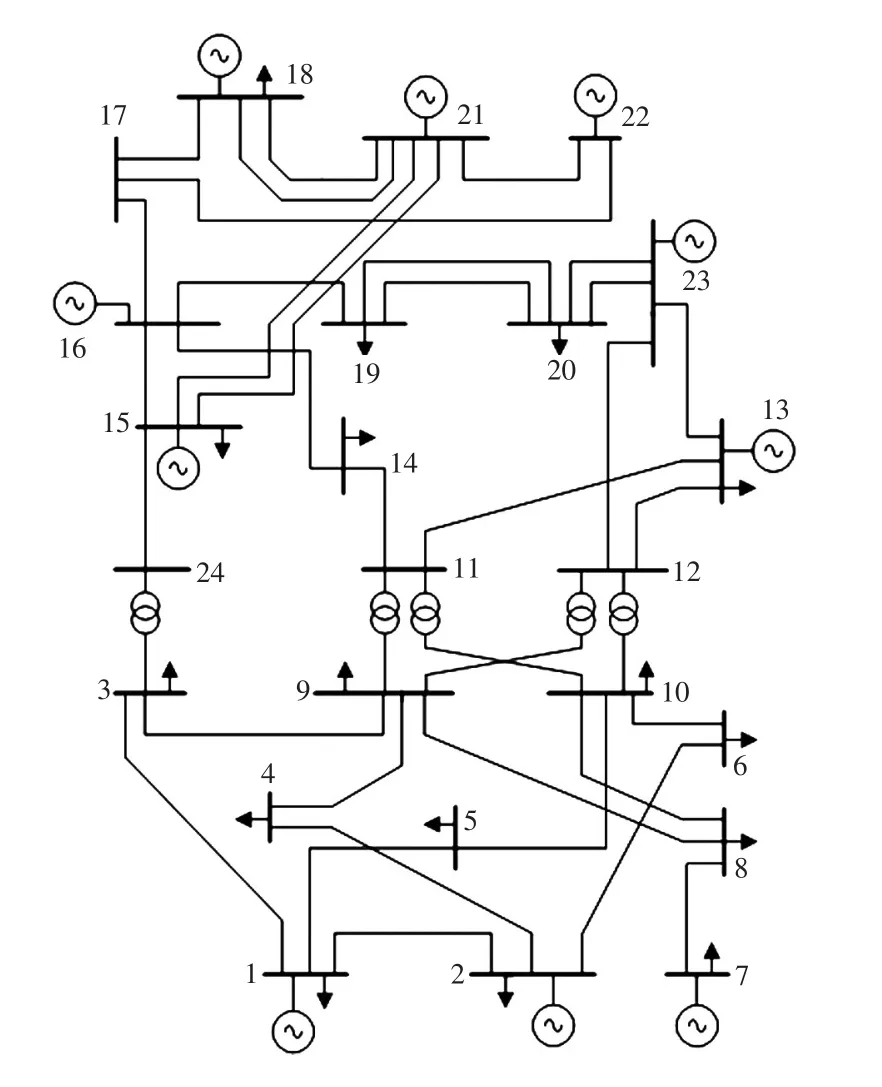
图2 IEEE RTS-24节点接线图Fig.2 Wiring diagram of IEEE RTS-24 system

各场景下的系统总负荷如图3所示。

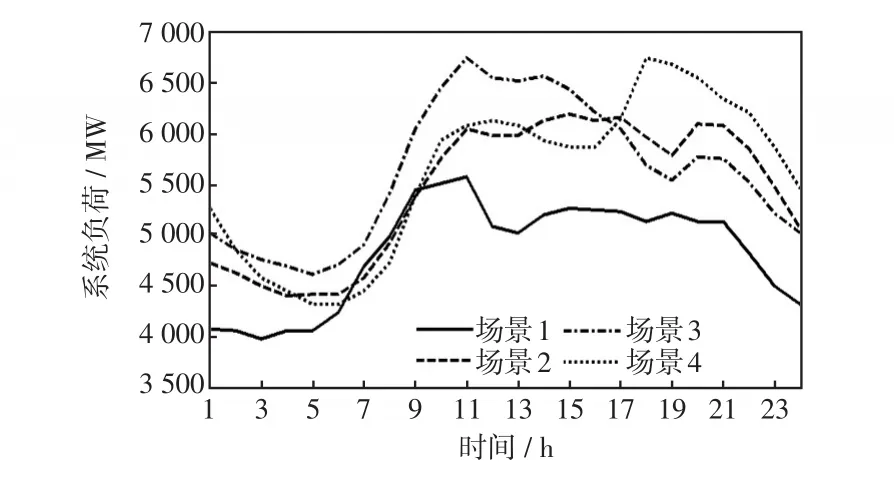
图3 各场景下系统的总负荷Fig.3 Total system load under each scenario

系统中所有机组的最大出力为7 762.5 MW，最小出力为2 321.6 MW。弃可再生能源的惩罚成本系数和切负荷的惩罚成本系数分别为1×103和1×106。所有新建线路均允许参与输电网结构优化；已有线路中，线路L17−22，L18−21（包含2条支路），L21−22允许参与输电网结构优化。

考虑机组组合和输电网结构优化的新建支路结果如图4所示。根据所提出的嵌入机组组合和输电网结构优化的含可再生能源系统规划方法，可得到在该系统中新建的支路（如图4中的粗实线所示）为：L1−8，L2−8，L6−7，L13−14，L14−23，L21−22，所对应的电网规划方案总成本为2.61×109$。

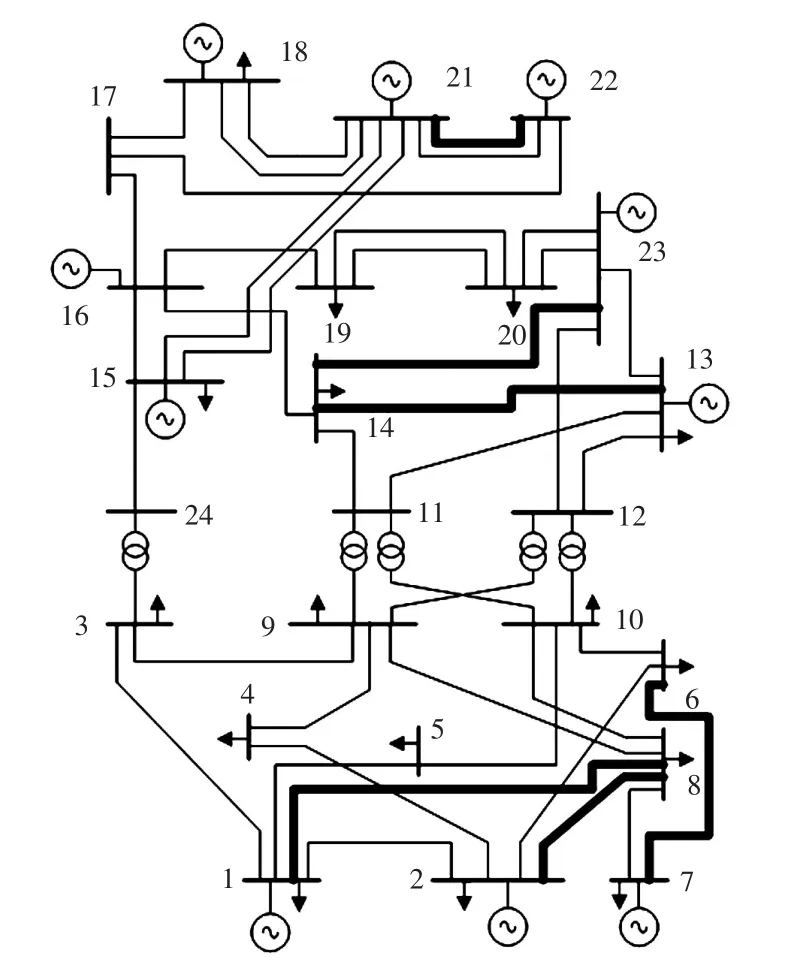
图4 考虑机组组合和输电网结构优化的新建支路结果Fig.4 Result of the newly built branch considering UC and OTS

各场景下对应的网络结构优化结果如图5所示（仅显示各场景下闭合断开状态发生变化的线路，0表示线路断开，1表示线路闭合；其余线路在各场景下均处于闭合状态）。

图5 各场景下网络结构优化结果Fig.5 Results of OTS under each scenario

以场景1为例，网络结构优化的结果如图6中虚线线路所示。

图6 场景1下网络结构优化结果示意Fig.6 Schematic of OTS results under Scenario 1

在高压区，支路L17−22以及节点B18和B21之间的两条支路均会被断开，这是因为节点B22处注入的功率，一部分经过节点B21注入节点B15并注入低压区，一部分经过节点B17注入节点B15并注入低压区，由于节点B17处也配置有风电场，因此支路L16−17更易发生阻塞。当支路L17−22以及节点B18和B21之间的2条支路均断开时，由节点B22处风电场等注入的功率可以由节点B15和B21间的支路注入节点B15并注入低压区，降低了网络中的阻塞风险。

在低压区，新建支路L2−8会被断开。可以看出，在低压区，存在多个电源节点向节点B8供电，当断开支路L2−8后，功率可以更平衡地流向其他节点，从而减少负荷削减的风险。

在场景1下，机组组合结果如图7所示（仅显示运行状态发生变化的机组，0表示停机，1表示开机运行；同一母线出可能存在多个机组，用（a）、（b）、（c）等进行区分）。

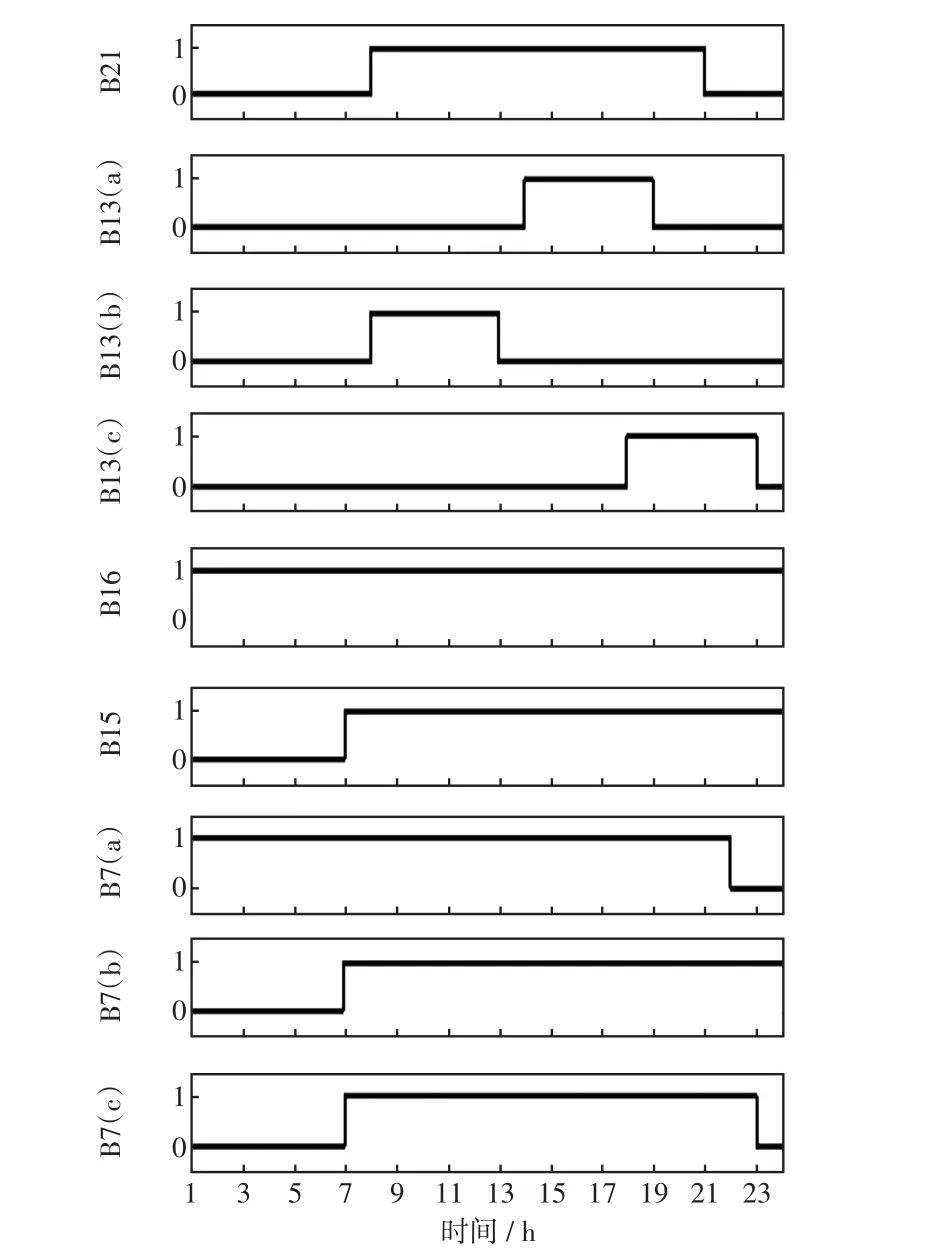
图7 场景1下的机组组合结果Fig.7 Results of UC under Scenario 1

为进一步验证所提方法的有效性，将所提嵌入输电网结构优化方法与不嵌入输电网结构优化方法进行比较。为叙述方便，将本文所提方法记为OTS方法，将对比方法记为NOTS方法。在NOTS方法下，新建支路为L1−8，L2−8，L6−7，L14−23，L19−23，L21−22，可见，考虑输电网结构优化将影响到具体的规划方案结果。

表1列出了2种方法下电网规划结果的各项成本对比，显然，在NOTS方法下，规划方案的总成本要高于OTS方法的总成本。具体而言，在不嵌入输电网结构优化时，系统的建设成本、运行成本、弃可再生能源成本均会更高。因此，考虑输电网结构优化，可以显著提升规划方案的经济性和对可再生能源的接纳能力。

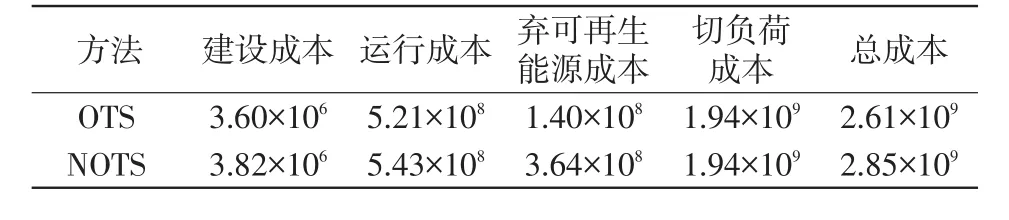
表1 规划方案的总成本及各项成本对比Tab.1 Comparison of total and detailed costs among planning schemes $

3 结语

本文针对目前研究中尚缺乏在含可再生能源电网规划中同时考虑机组组合和输电网结构化的问题，建立了嵌入机组组合和网络结构优化的可再生能源接入系统的电网规划模型，借助机组组合和网络结构优化，系统分析电网规划方案的经济性，并通过IEEE RTS−24算例系统和对比分析验证了所提方法的有效性。结果表明，通过嵌入机组组合和输电网结构化，所提方法能较好地提升规划方案的经济性与对可再生能源的接纳能力。