考虑保修服务的制造/再制造融合产品优化配置研究*
姚星辰 周 敏
(①武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉 430081;②武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉 430081)
再制造业具有节约资源,降低环境污染的特点。随着环境破坏和能源短缺等问题日渐严重,国家已经将再制造产业列为发展目标,作为“中国制造2025”的重要部分。在经济和环境的双重效益下,许多原始制造企业也开始积极的实施再制造,对于制造/再制造融合的产品和生产系统的研究越来越重要。但由于再制造零部件质量和数量的不确定、不稳定性以及客户对其功能质量信心不足等因素增加了产品设计和生产的难度[1],制造与再制造零部件组合的有关产品配置优化理论落后于实践。
随着再制造工艺的发展,再制造产品的性能和质量都将不亚于原先的产品。对制造与再制造融合的产品优化配置的有效研究有利于提高再制造产品的利用率,包含再制造零部件的汽车,机床等将拥有更广阔的市场。但传统客户对再制造件仍然存在顾虑,而良好的售后保修服务能够提高客户对于产品的满意程度[2]。本文从保修服务的角度展开分析,对制造和再制造融合的产品配置问题进行了研究。
在提高产品服务性方面,传统的研究集中在产品的保修政策上。如Chang和Lin[3]针对大型精密产品,探讨了制造商在产品生命周期内进行预防性维护措施以及通过延长保修期最大化预期利润。李浩、刘根[4]则构建了基于NSGA-Ⅱ产品服务系统多目标优化配置设计。Darghouth[5]等分析了保修期内免费、保修期后收费两阶段的总利润,据此制定了产品维护周期。M.Park等[6]研究了可更新保修期下,制造商的最佳维护政策。卢丽丽[7]依据某汽车售后维修数据来分析汽车的故障分布,在二维保修策略的基础上构建成本模型,分析了由于里程变化引起的故障率分布及成本。仝鹏、刘子先[8]研究了基于使用率的汽车二维延保策略,以不完全维修和最小维修两种方式确立了成本最优化模型。虽然针对产品售后策略的研究很多,但都是针对新品,对再制造品进行服务模块创新的研究较少。
由于某些零件既可以用制造也可以用再制造方式进行生产,因此本文从多种保修服务角度出发,结合再制造产品的模块化划分方法构建保修服务模块和产品模块,讨论在保修利润,产品成本和绿色环保等情况下对制造与再制造融合的产品配置模块多目标优化,以得到不同保修服务模块下的最佳产品配置。考虑保修服务的制造与再制造产品模块优化配置方案如图1所示。
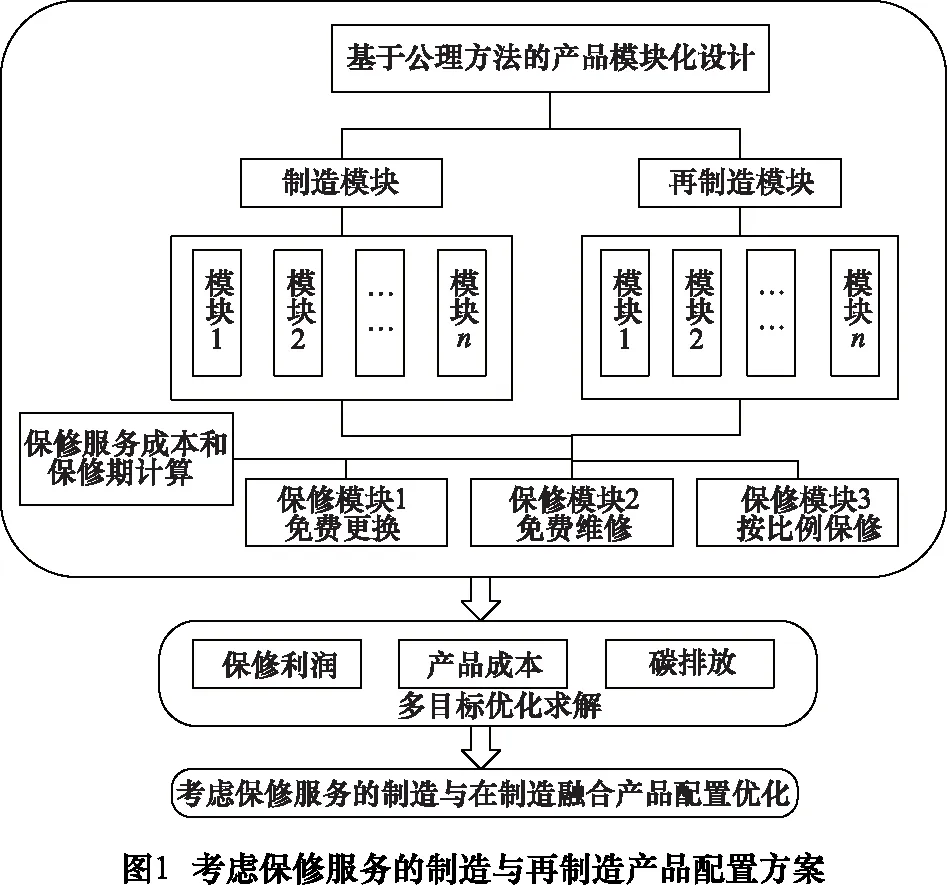
1 基于保修服务的产品分析
对产品的售后服务能够有效地增加客户的满意程度,人性化、标准化的售后服务理念以及规范的售后服务标准能够确保售后服务细致化和精致化,大幅度提高客户对于产品的依赖程度,推动产品的可持续发展[8]。目前较为流行的售后服务包括对产品的安装、调试、提供技术指导、定期维护和保养、电话回访以及对产品实行“三包”等。但对于大多数产品尤其是再制造产品,产品质量仍然是决定性因素,因此对产品提供相适应的保修服务非常重要。
1.1 保修服务类型
保修服务是厂商提供给客户的能够保证产品质量的服务手段,它能够促进产品的销售,提高客户满意程度。根据保修服务的赔偿方式可将其分为免费更换保修、免费维修保修、按比例保修及终身服务保修[9]。
免费更换保修,即在保修期内生产者承担产品更换的所有成本,常适用于不可维修或价格较便宜的产品;免费维修保修,即生产者在保修期内承担维修的所有成本,适用于可维修产品;按比例保修,即在保修期内生产者和客户按照一定比例承担保修的一定费用;组合保修,包括了上述3种保修特点;终身服务保修,常用于昂贵、易损耗及复杂的产品。本文选择免费更换保修、免费维修保修和按比例保修进行分析。
1.2 保修成本和保修期分析
虽然保修服务能够潜在提高客户的购买欲望,但额外增加了厂商的成本,一方面如果厂商通过缩短保修期、减少被保零部件等措施来一味降低保修成本,可能会导致客户满意程度下降;另一方面如果厂商承担保修期内产品保修的所有费用来提高客户满意度,也可能会导致成本过高而亏损。因此,针对不同的产品根据寿命和可靠度等计算保修期和保修成本显得尤为重要。
产品在保修期内发生故障,就需要及时进行修理。通常用故障率r(t)来表示单位时间产品发生故障的概率,用故障概率密度函数f(t)表示任意时刻t,产品单位时间内发生故障的概率,它和产品的可靠度F(t)相关,一般为不可靠度的导数。
(1)
威布尔分布是常用的概率分布函数,它能够描述产品生命周期内多个阶段的失效分布特征[10],用威布尔分布表示产品在保修期内的故障次数,其表达式如下:

(2)
设Qm为单位零件在不用保修服务模式下的总成本,qm不同保修服务下的基础成本,则有
Qm=qm×λ(t)
(3)
当逐步提高保修期后,客户满意度提升,用S表示不包含保修成本的基础利润,当提高保修时间,随之销售量N(t)会增加,企业利润会有增长,但过长的保修期也会导致企业成本增大,利润下降,因此可将利润W(t)看作随保修时长t先增后减的函数。设销售量N(t)是随着厂商提供保修服务策略m和保修时长t变化而变换的函数,为简化分析,采用线性函数,则
N(t)=kmt+c
(4)
W(t)=[S-QM]·Nm(t)
(5)

图2为保修利润的凸函数,当保修时间为t时,总体利润最高,最优保修期为t*,可通过下式求得:
(6)
2 基于保修服务的制造/再制造融合产品模块划分
运用公理设计方法根据功能需求初步分解产品结构,根据子结构功能和结构的相关程度进行相关度分析,得到模糊矩阵R[11]。依据模糊矩阵和模糊树图的方法计算产品模块相关度,通过选取不同的阈值对最大生成树中权值小于的边进行截割,选取不同的阈值得到产品模块划分结果[12]。
产品功能和结构相关度评价准则可由表1表示。
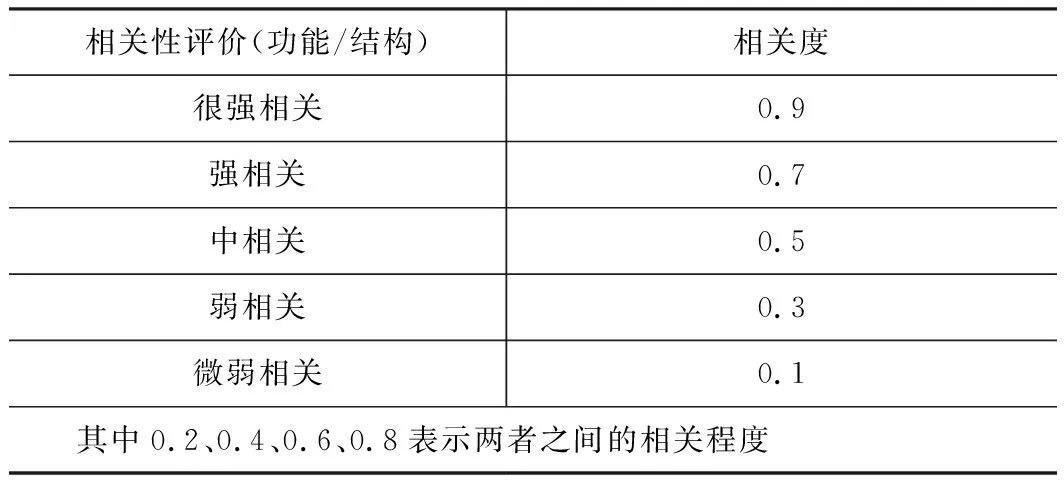
表1 产品功能结构相关度评价
对于包含再制造零部件的产品,其结构应该单独划分出来,以方便分析。结合上文的产品保修服务方式,根据公式计算不同保修方式下产品各个模块的保修年限和成本,就可得到产品在该保修模块下的成本和保修服务年限,再将各个保修服务作为一个模块,以便进行产品模块化配置优化。

3 产品优化配置适应度函数构建
在多种保修服务模块的条件下,制造与再制造产品优化配置需要保证成本、环保和利润等方面的要求,通过产品适应度目标函数给予约束,采用基于NSGA-Ⅱ改进的一种多目标优化算法进行求解,建立以产品成本、绿色环保和保修利润为目标的多目标优化模型进行求解以得到制造和再制造零部件融合的配置方案。
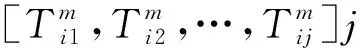
3.1 产品成本和利润函数
生产制造零部件和再制造零部件所需要的成本不相同,企业需要最小成本的模块组合方式,才能实现利益最大化。在不考虑库存成本的情况下,制造和再制造模块组合的产品成本如式(8)。
增加保修时长和更改保修策略都会引起产品销售量的变化,将由保修策略m和保修时长t引起利润的变化作为保修利润W的目标函数,如式(9)。
F(Mk)=minF(Mk)
(7)
(8)
(9)
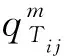
3.2 碳排放量
制造与再制造组合的产品的绿色环保度用碳排放量来衡量。为了满足企业生产需求,有时需对碳排放量进行一定的约束。
F(Ck)=minF(Ck)
(10)
(11)
式中:UTij表示i种制造方式下生产j模块的碳排放量。
则有关制造与再制造组合产品优化配置的目标函数为:
F(x)=[minF(Mk),maxW,minF(Ck)]
(12)
F(Mk)=minF(Mk)
F(Ck)=minF(Ck)
(13)
3.3 考虑保修服务的多目标函数优化
NGSA-Ⅱ是基于NSGA改进的一种遗传算法,具有搜索能力强,解的分布和覆盖大等特点,广泛用于产品设计和工程优化等问题。在制造与再制造融合产品配置中,依据上述模型得到一组最优解,辅助设计师选择,使用MATLAB进行编程,求出Pareto解集对以保修服务利润、产品成本和碳排量为约束目标的函数进行分析,图4是NSGA-Ⅱ求解流程。
4 实例分析
以某汽车公司为例,通过上述方法对该公司考虑多种保修服务的制造与再制造零部件融合的汽车产品优化配置方法进行验证。
通过制作SD调查问卷对该公司汽车潜在客户进行调查,调查主要针对客户对于该公司再制造汽车在多种保修服务以及该保修服务下随保修期增加的有意购买人数,以该数据作为销售量Nm(t)的样本数据,调查对象180人,实际调查176人,其参数如表2。

表2 客户在多种保修策略下购买倾向
经过计算,可以得到3种保修服务模式下的销售量曲线,在服务年限t≥0情况下对于免费更换服务,N1(t)=22t+82;对于免费维修服务,N2(t)=18t+82;对于按比例保修服务,N3(t)=15t+82。
基于公理设计,考虑再制造模块对汽车进行有关结构拆分。其中功能结构零部件可分为4类,有:D1(P10发动机);D2(P20发电机、P21车灯、P22起动机、P23电源、P24仪表盘);D3(P30车桥、P31离合器、P32变速箱、P33传动装置、P34悬架、P35转向器、P36转向装置、P37制动机构);D4(P40座椅、P41车门、P42车顶、P43车架、P44车轮)。根据子结构功能和结构相关性评价,计算确定各个零部件之间的相关关系,得到各个模块之间模糊关系矩阵,如图5。
在制造与再制造融合产品配置中,再制造零部件非常重要,因此对于再制造汽车,首要将再制造零部件单独划分出来,包括发动机、起动机、发电机、变速箱和转向器。

结合模糊矩阵和模糊树图的方法,取阈值为0.24,最终得到划分方法:M1[P11];M2[P20];M3[P22];M4[P31];M5[P32];M6[P35];M7[P21,P23,P24];M8[P33,P34,P36,P44];M9[P30,P37,P40,P41,P42,P43],为T1-T9共9个模块。
对可进行保修服务的模块进行分析,确定不同保修服务中各模块的保修期和保修成本,已知该企业制造和再制造发动机的故障次数和3种服务模块下基础保修成本如表3、4。

表3 发动机的故障次数

表4 发动机保修成本
根据式(6)计算最佳保修期,制造发动机在免费更换、免费维修、按比例保修的保修期为1.8、3和5年,再制造发动机在免费更换、免费维修、按比例保修的保修期为1.75、3和4.5年。同理可得各个可再制造模块的保修期为表5所示。
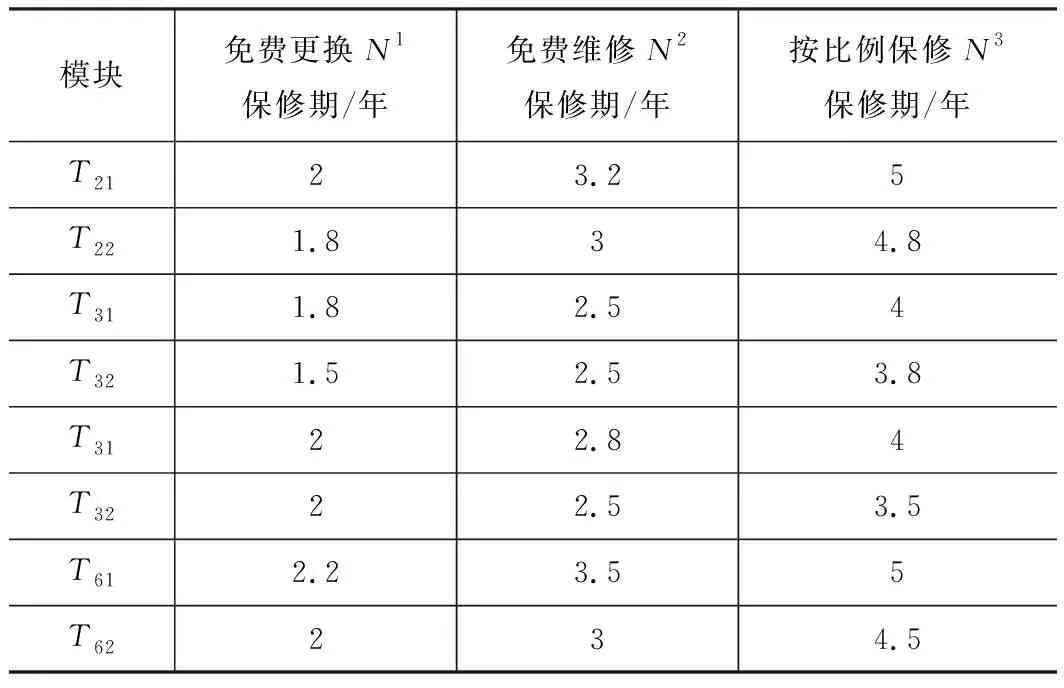
表5 各个模块不同保修方式下保修期
根据该企业提供的资料,该型号汽车匹配的9个模块制造和再制造模块的成本、碳排放量以及保修期内不同保修服务成本如表6、7所示。
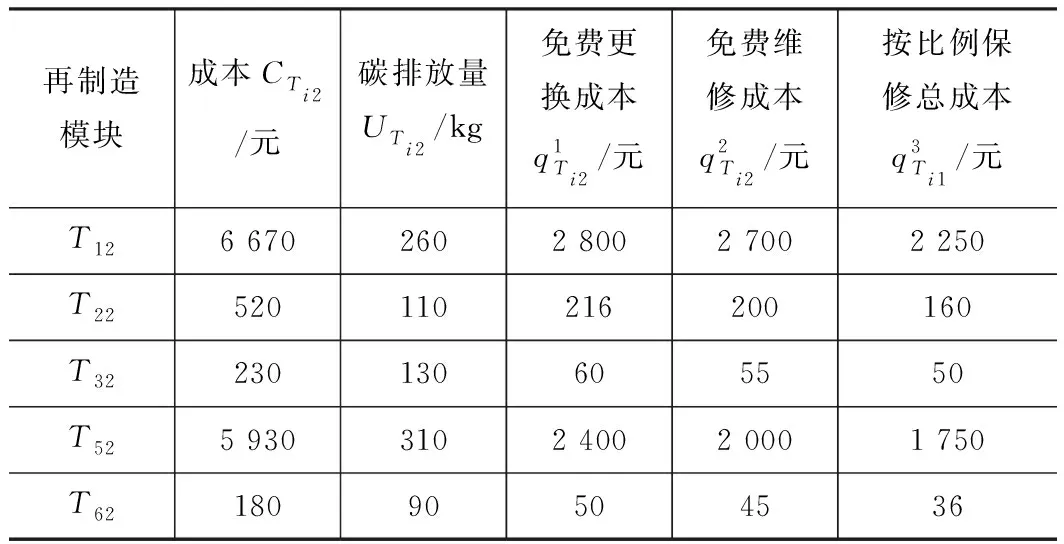
表6 再制造模块成本、碳排放、保修成本

表7 制造模块成本、碳排放、保修成本
本文采用MATLAB 2016b对以碳排量、产品成本和保修利润3个目标为适应度函数的产品配置方案进行求解,设计最大进化代数200,内部种群规模为100。为简化模型,可忽略无法再制造的模块,将上述数据代入式(13)求解,最终得到Pareto前沿图如图6所示,基于Pareto解所对应的汽车模块设初始方案如表8。
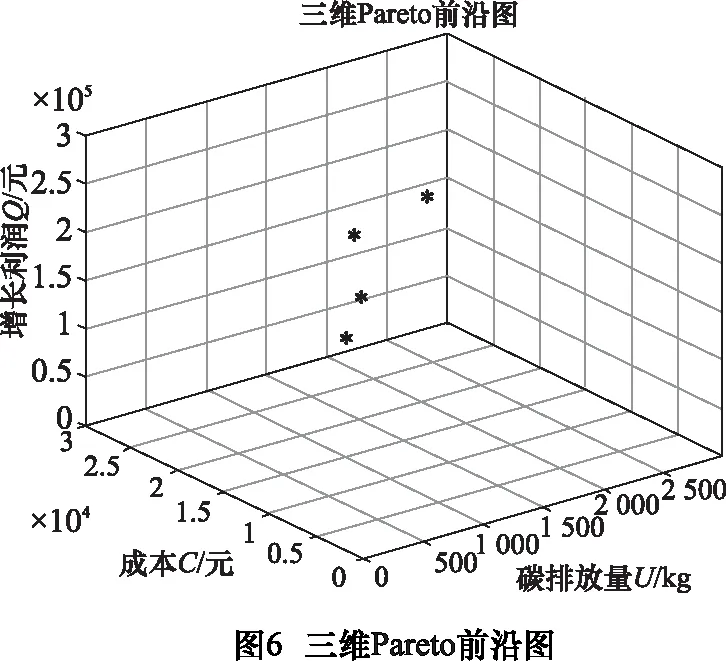
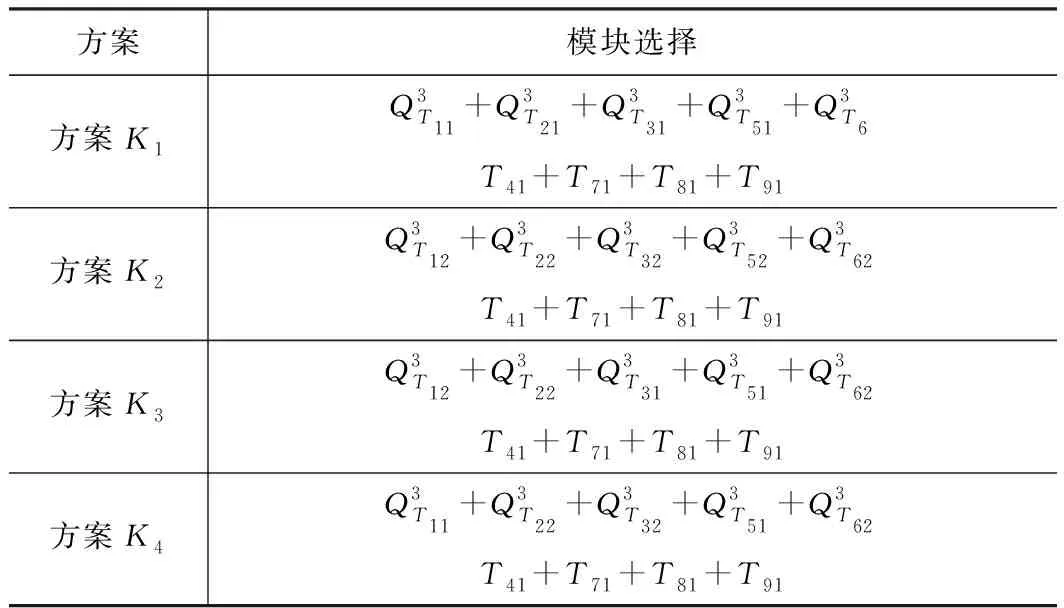
表8 Pareto解所对应的汽车模块配置初始方案
表9是求解的四种方案的利润、碳排放和成本。根据上述方案分析,可以看出虽然再制造产品在生产成本和碳排量方面优于制造产品,但由于客户的购买倾向不高,企业利润并不是最大,通过不同保修模块提升客户购买倾向,再制造品的利润得到了提高,制造与再制造融合的产品有了更大的市场。

表9 各方案保修利润、碳排放、成本
采用上述方案进行产品配置优化,厂商针对性的提出了不同零部件的保修方案,既提高了客户对于再制造品的购买倾向,也使得企业在不同保修方案的利益达到最大化,同时在碳排放和生产成本方面也达到了整体最优。相较于以往对于产品的外形设计和满意度设计,上述方案通过对考虑保修服务的再制造设计,避免了客户对于再制造品信心不足等问题,有利于提升再制造品的市场空间,提高企业效益。
在实际设计中,企业也可以考虑不同需求市场,设置目标权重,可以针对性的选择不同组合的产品配置和保修方案。
5 结语
本文针对制造与再制造融合产品,为了解决客户对于再制造品信心不足的问题,构建了一种面向不同保修服务的模块化产品优化配置方法,考虑不同保修服务对于客户再制造品的购买提升,以保修利润增加、碳排量、成本3个目标为优化对象,通过NGSA-Ⅱ遗传算法对上述目标进行求解,使得产品配置满足客户需求和企业生产,提升再制造品的市场空间。针对该方案,以某汽车公司针对不同保修服务展开汽车模块化设计和多目标模型求解为例,得到了整体最优解,验证了方案的可行性。
但是该模型只考虑了维修售后服务模块的设计方案,没有详细地对产品售后服务系统多样化服务方式进行分析。同时,在实际订单中,针对详细订单的产品配置方案也需要考虑再制造率、回收不确定性、库存量、库存成本等要素。因此本文将以此为基础,进一步融合产品售后、再制造约束、技术、工艺、售价等因素完善产品配置方案。

