塑性流动挤出切削制备梯度结构铝薄板的仿真分析*
邹银辉 邓文君
(华南理工大学机械与汽车工程学院,广东 广州 510640)
大塑性变形(severe plastic deformation,SPD)工艺作为提高材料性能的可行方法之一,得到了广泛的关注。迄今为止,相关研究人员已经提出了许多SPD工艺,例如等通道转角挤压(equal channel angular pressing,ECAP)[1-2]、高压扭转(high pressuretorsion,HPT)[3-4]、累积叠轧(accumulative roll bonding,ARB)[5-6]、扭转挤压(twist extrusion,TE)[7-8]与大应变挤出切削(large strain extrusion machining,LSEM)[9-11]等。SPD工艺最为显著的优势是能够在室温下将材料的初始粗大晶粒转化为超细晶粒,从而使其机械强度明显提高[12-13]。但是,目前绝大多数SPD工艺在使材料得到较高机械强度的同时,延展性不可避免地出现显著降低,这很大程度上限制了SPD工艺在工业上的应用[14-16]。因此,寻找一种可以兼顾材料高强度与高塑性的新型工艺尤为重要。
Vu V Q等[17]提出了一种新型的SPD工艺-塑性流动挤出切削(plastic flow machining,PFM)工艺,通过可控的侧向挤出切削过程将大块工件的表层分离出来,并将其转化为具有超细晶粒与梯度结构的薄板[18]。所制备的梯度结构铝薄板沿厚度方向呈现明显应变梯度,且晶粒尺寸由一侧的超细晶粒逐渐过渡到另一侧的粗大晶粒[19-20],其强度明显增大,延展性也得到了极大提高。Vu V Q等[21]通过实验表明,PFM工艺制备的商用纯铝Al1050薄板的抗拉强度提高到原材料的3倍,均匀延展性约6%,且其各向异性系数为0.92,大于传统轧制(0.5~0.85),而较高的各向异性系数对提高铝板的成形性具有重要意义。但是,该实验均在同一模具中进行,没有改变其结构参数,即缺少模具结构对梯度结构薄板成形影响的相关研究。这在研究上是有所不足的,因为就该工艺而言,模具结构对梯度结构薄板成形起到了关键甚至决定性的作用,研究其对薄板成形的影响十分必要。
本文采用DEFORM软件,对不同模具结构下梯度结构铝薄板的成形进行了模拟仿真,研究分析了其对梯度结构铝薄板侧向挤压比及等效应变的影响,为梯度结构铝薄板的制备提供借鉴。
1 PFM工艺的原理
PFM工艺原理如图1所示,初始工件高度为H,宽度为D(垂直纸面方向),模拟中统一取为20 mm,即工件横截面为一正方形。通过压力P将工件以恒定速度压入水平方槽模具中,经挤压后其高度缩减为H1,模拟中统一取为17.5 mm,故挤压厚度H2=H-H1=2.5 mm。模具侧面有一个长方形开口,模拟中统一取开口宽度h为1 mm,开口长度l(垂直纸面方向)等于初始工件宽度D,即l=D=20 mm。Hill R[17]研究表明,当厚度比r=H2/H的取值在0.01~0.15时,高压区域附近被塑化的材料很容易流入细缝之中,而本研究中r恒等于0.125,满足上述条件,故模拟过程中材料也可从侧向开口挤出。采用恒定压力Pb作为背向压力,以控制材料流动。开口左侧与横向通道之间存在圆角,即开口圆角R。开口右侧与横向通道之间存在拐角,即挤压角度C。由于R和C均与梯度结构薄板成形密切相关,且它们都比较容易控制,故选用这两个参数作为变量对不同梯度结构铝薄板的成形进行研究。
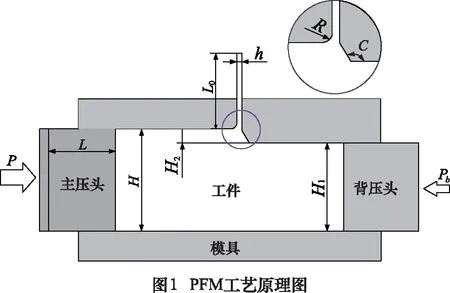
作为一种金属成型工艺,PFM工艺与传统的切削加工工艺存在许多相似之处,但有着本质的区别。在PFM工艺中,材料分离基于高压应力下材料的塑性流动。而传统切削加工中,材料分离直接由刀具产生,所涉及应力为拉应力。因此,两者的成形原理完全不同。
2 有限元模拟
2.1 模型设置与材料建模
由于模具中侧向开口的长度l远大于宽度h,满足平面应变条件,故本文将原始模型转换为较为简单的平面应变模型,采用基于拉格朗日公式的大塑性变形分析软件DEFORM-2D进行模拟。

将工件材料定义为ALUMINUM-1050A,采用基于Hollomon函数[22]的冯米塞斯模型:
(1)
式中:σ为等效应力,MPa;ε为等效应变;n为应变指数;m为应变率指数;c与y均为与材料相关的常数。利用Arzaghi M等[23]研究所得Al1050的应力-应变曲线确定了相关参数,如表1所示。
表1 Al1050的冯米塞斯模型相关参数

表1 Al1050的冯米塞斯模型相关参数
符号nmcy取值0.2301800
2.2 热物理特性与摩擦模型
在室温下,SPD工艺过程中温度升高很不明显。对于铝材而言,其温升一般不会超过5 ℃,例如Zhilyaev A P等[24]采用变形最为剧烈的SPD工艺-HPT制备铝材,其温升也只有接近5 ℃,这主要由于材料变形缓慢所造成。本研究中主压头速度恒为1 mm/s,材料变形缓慢,温升不大,对薄板成形影响很小,故可忽略其热物理特性。
2.3 评价指标
为了描述梯度结构铝薄板的成形效果,本文引入侧向挤压比x、左侧等效应变εL及右侧等效应变εR作为评价指标,其中侧向挤压比x是指薄板成形体积V0与工件挤入体积V的比值。
如图1所示,由于模拟步数为1 600步,步长深度为0.025 mm,故工件挤入长度L=1 600×0.025 mm=40 mm。对于所制备的梯度结构铝薄板,其厚度(沿压力P方向)基本等于开口宽度h,可用h代替,宽度(垂直纸面方向)基本等于开口长度l,可用l代替,并将侧向挤出距离定义为薄板长度L0(沿挤出方向)。因此,所求侧向挤压比
(2)
式中:x为侧向挤压比;L0为梯度结构铝薄板长度,mm。
此外,将所制备的梯度结构铝薄板的左侧等效应变εL及右侧等效应变εR作为另两个评价指标,以更好地描述其成形效果。
3 模拟结果与讨论
为了更好地解释挤出切削过程中金属的塑性流动,本文对PFM模型材料塑性流动的区域进行了划分,并将经侧向开口挤出的材料与经横向通道流出材料之间的边界定义为材料分流边界,即材料分流边界以上的材料基本经开口挤出,而材料分流边界以下的材料基本经横向通道流出。如图3所示,当材料横向流动阻力较小或开口挤出阻力较大时,材料分流边界位于区域1,材料很难经开口挤出,故从开口挤出的材料相对较少;当材料横向流动阻力增大或开口挤出阻力减小时,材料分流边界位于区域2,故从开口挤出的材料有所提高;当材料横向流动阻力很大或开口挤出阻力很小时,材料分流边界位于区域3,大部分材料经开口挤出,故从开口挤出的材料接近峰值。

3.1 开口圆角对铝薄板成形影响分析
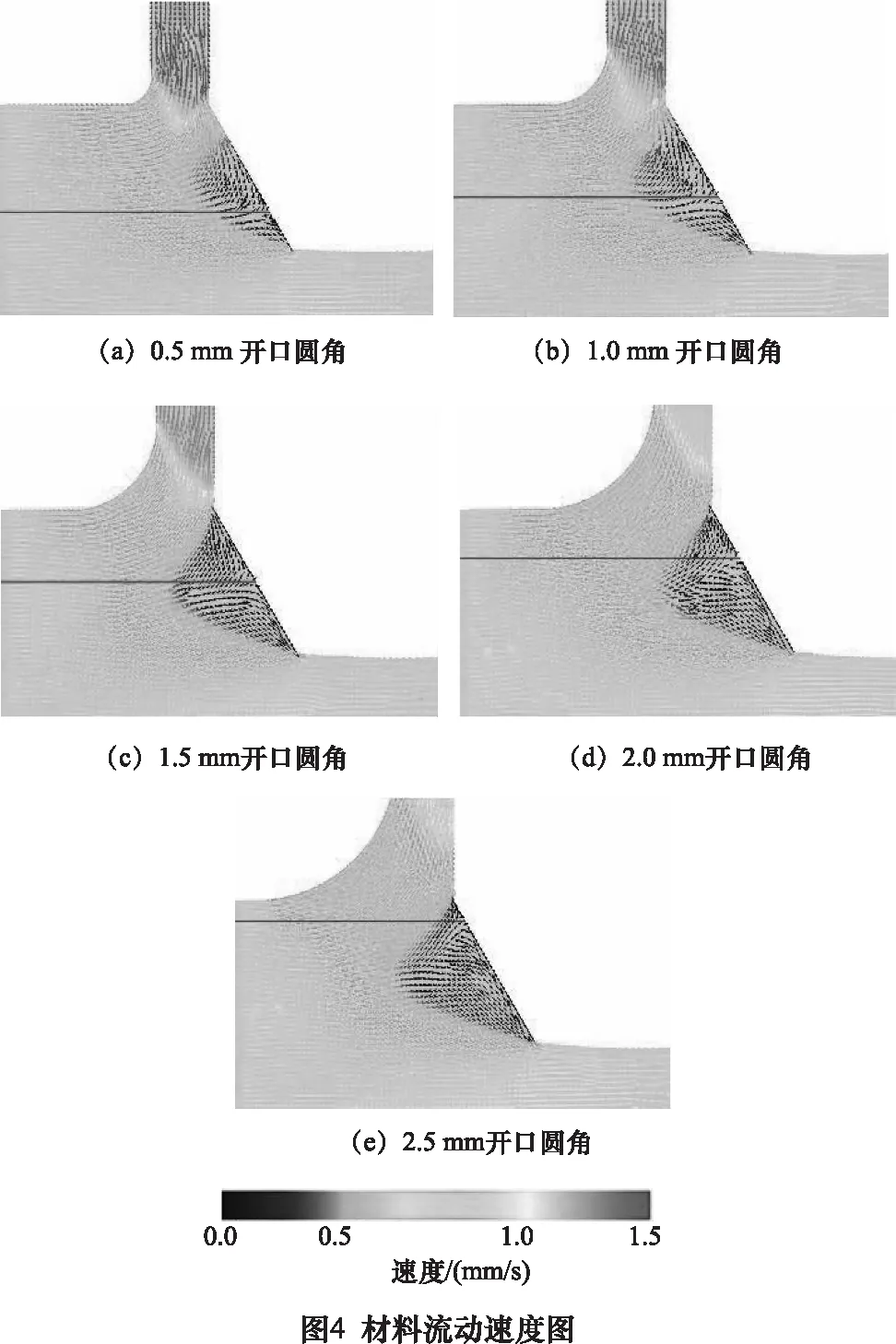
为了分析开口圆角对梯度结构铝薄板成形的影响,本节在保证挤压角度C为120°的前提下,模拟了开口圆角R在0.5 ~2.5 mm梯度结构铝薄板成形的结果,其中材料流动速度如图4所示,材料分流边界由实线标出。
由图5可以看出,随着开口圆角R的增大,梯度结构铝薄板的侧向挤压比x逐渐减小。
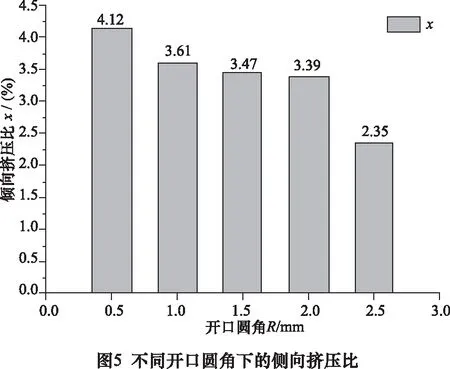
由图4可知,这是因为当R为0.5 mm时,材料横向流动阻力相对较大,开口挤出阻力相对较小,材料分流边界位于区域2,且开口附近材料流动速度较快,故较多的材料从开口挤出,侧向挤压比x较大。当R从0.5 mm逐渐增大到2.5 mm时,材料横向流动阻力逐渐减小,开口挤出阻力逐渐增大,材料分流边界由区域2逐渐过渡到区域1,且开口附近材料流动速度也逐渐减慢,故较少的材料从开口挤出,侧向挤压比x逐渐减小。
3.1.2 开口圆角对铝薄板等效应变的影响分析
对于开口圆角R在0.5~2.5 mm的模拟结果,其等效应变如图6所示。分别测量开口附近挤出铝薄板左右两侧的等效应变值,其结果如图7所示。


由图7可以看出,随着开口圆角R的增大,梯度结构铝薄板左侧等效应变εL逐渐增大。当开口圆角R1.5 mm时,梯度结构铝薄板右侧等效应变εR随R的增大而增大,当R1.5 mm时,εR随R的增大而减小。当R为1.5 mm时,εR与εL之差最大。
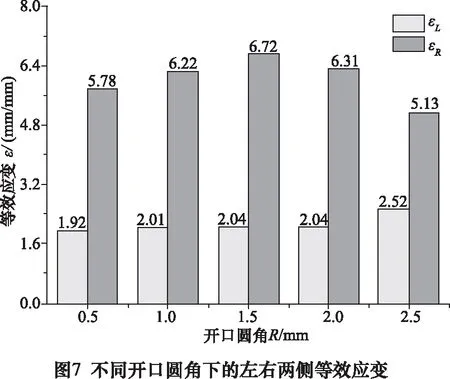
由图4可知,这是因为对于薄板左侧,当R从0.5 mm逐渐增大到2.5 mm时,圆角过渡作用逐渐增大,材料更加容易流入薄板左侧,塞积现象较严重,晶粒之间相互作用较大,且开口附近材料流动速度逐渐减慢,与开口侧壁摩擦作用较充分,故左侧等效应变εL逐渐增大。然而,对于薄板右侧,当R1.5 mm时,随着R的增大,开口附近材料流动速度逐渐减慢,与开口侧壁摩擦作用较充分,虽然材料分流边界有所上移,但效果弱于摩擦作用,故εR逐渐增大。当R1.5 mm时,随着R的增大,材料分流边界由区域1与区域2的交界处逐渐上移到区域1顶部,流入薄板右侧的材料减少,塞积现象较微弱,晶粒之间相互作用较小,虽然开口附近材料流动速度仍然减慢,但效果弱于晶粒之间相互作用,故εR逐渐减小。
3.2 挤压角度对铝薄板成形影响分析
为了分析挤压角度对梯度结构铝薄板成形的影响,本节在保证开口圆角R为1.5mm的前提下,模拟了挤压角度C在100°~140°梯度结构铝薄板成形的结果,其中材料流动速度如图8所示,材料分流边界由实线标出。

3.2.1 挤压角度对铝薄板侧向挤压比的影响分析
对于挤压角度C在100°~140°的模拟结果,分别测量其挤出铝薄板长度L0,并据式(2)计算相应的侧向挤压比x,结果如图9所示。
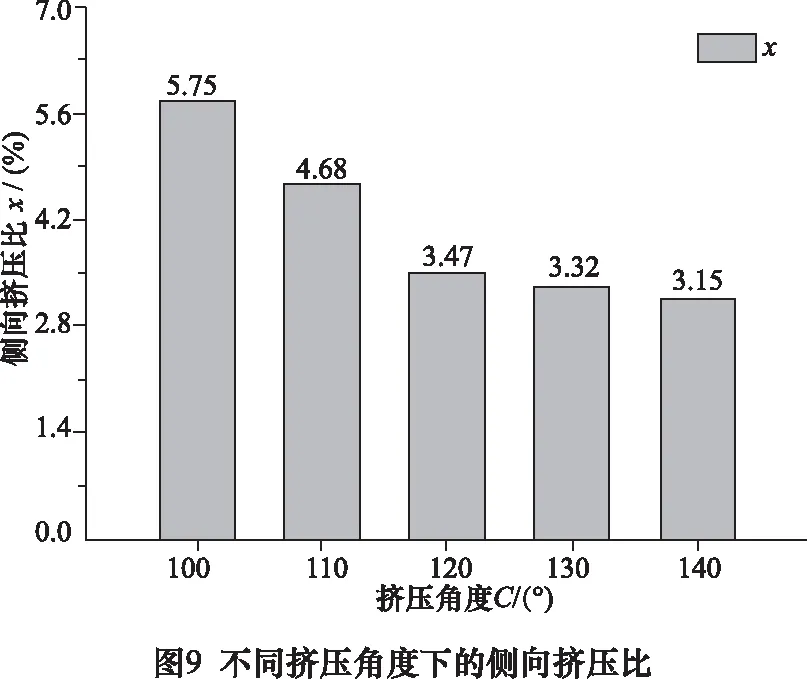
由图9可以看出,随着挤压角度C的增大,梯度结构薄板侧向挤压比x逐渐减小。
由图8可知,这是因为当C为100°或110°时,材料分流边界位于区域2底部,且开口附近材料流动速度较快,故较多的材料从开口挤出,侧向挤压比x较大。当C为120°时,材料分流边界迅速上移,位于区域1与区域2的交界处,且开口附近材料流动速度减慢,故从开口挤出的材料减少,侧向挤压比x减小。当C为130°或140°时,材料分流边界再次迅速上移到区域1顶部,且开口附近材料流动速度减慢,故较少的材料从开口挤出,侧向挤压比x较小。由此可见,当C在110°和130°之间变化时,材料分流边界上移速度很高,可作进一步研究。

3.2.2 挤压角度对铝薄板等效应变的影响分析
对于挤压角度C在100°~140°的模拟结果,等效应变如图10所示。分别测量开口附近挤出铝薄板左右两侧的等效应变值,结果如图11所示。
由图11可以看出,随着挤压角度C的增大,梯度结构铝薄板左侧等效应变εL逐渐减小。当挤压角度C120°时,梯度结构铝薄板右侧等效应变εR整体上随R的增大而增大,当R120°时,εR随R的增大而减小。当C为120°时,εR与εL之差最大。
由图8可知,这是因为对于薄板左侧,当C从100°逐渐增大到140°时,材料分流边界由区域2底部逐渐上移到区域1顶部,从开口挤出的材料减少,塞积现象减弱,晶粒之间相互作用减小,虽然开口附近材料流动速度逐渐减慢,但效果弱于晶粒之间相互作用,故左侧等效应变εL逐渐减小。然而,对于薄板右侧,当C120°时,随着C的增大,开口附近材料流动速度逐渐减慢,与开口侧壁摩擦作用较为充分,虽然材料分流边界有所上移,但效果弱于摩擦作用,故εR整体上逐渐增大。当C120°时,随着C的增大,材料分流边界迅速上移,从开口挤出的材料减少,塞积现象减弱,晶粒之间相互作用减小,虽然开口附近材料流动速度仍减慢,但效果弱于晶粒之间相互作用,故右侧等效应变εR逐渐减小。
4 结语
本文采用控制变量法,对不同开口圆角R与挤压角度C下梯度结构铝薄板的成形进行仿真分析,所用材料模型与文献[18]及[21]中的材料模型完全一致,且所得模拟结果与文献[18]及[21]中的数值分析结果及实验趋势基本相符,故证明该模拟结果具有较高的可信度。最终,得出了R与C对梯度结构薄板侧向挤压比及等效应变的影响规律,总结如下:
(1)随着R的增大,梯度结构铝薄板侧向挤压比x逐渐减小,左侧等效应变εL逐渐增大,右侧等效应变εR呈现先增大后减小的趋势。当R为1.5 mm时,εR与εL之差最大。
(2)随着挤压角度C的增大,梯度结构铝薄板侧向挤压比x逐渐减小,左侧等效应变εL逐渐减小,右侧等效应变εR整体上呈现先增大后减小的趋势。当C为120°时,εR与εL之差最大。
(3)在保证PFM模具其他结构不变的前提下,取R为1.5 mm及C为120°时,所制备铝薄板的应变梯度最为明显。

