基于服装含水率的PHS 模型改进

李杨 邹钺

东华大学环境科学与工程学院

在过去的几十年中，与高温环境相关的高发病率和死亡率成为了主要的紧急公共卫生问题之一[1-2]。尽管现在人类已经在各种热环境的生理适应方面有了很大的进步，但是对于现有的大多数的热调节模型来说，准确地预测热应变仍然是一个巨大的挑战[3]。其中预测热应变PHS 模型（Predicted Heat Strain）的应用较为广泛，并且被ISO 7933 采用。然而PHS 模型的理论基础是热平衡方程，在人体与环境进行热交换时，除了周围的环境以及人体的活动强度等参数，服装热阻对于人体与环境的换热是一个十分重要的参数。但是在PHS 模型的使用中，并没有考虑到当人体处于劳动状态时身体所排出的汗液会将服装打湿。由于服装的汗湿，其热阻可能会随着不同的润湿程度而不断的变化，不再是一个恒定值，而是一个动态变化值。本文通过汗湿服装的热阻试验数据对比进行修正PHS 模型，使其更加接近实际情况以更加准确的预测人员的安全劳动时间。

1 PHS 模型修正

1.1 PHS 模型简介

在1989 年首次公布该标准的时候，受到了外界的大量质疑，将其与Haslam[4]、Smolander[5]的试验数据做对比，发现预测结果与试验结果存在很大的偏差。之后大量的学者对其进行不断的改进，如Mehnert[6]等开发了一种新的预测平均皮肤温度的模型对PHS 模型进行修正，并验证了其合理性，从而提高了PHS 模型的有效性。Parsons 和Havenith[7-8]等人针对服装热阻提出了合理的修正，将服装热阻与人的移动以及周围风速的大小建立了联系，从而建立了动态服装热阻的概念。Malchaire[9]结合原模型仅对具有正常反射率特性的服装有效的缺点，提出了修正系数FclR。基于欧洲8 个热生理学试验室的672 个试验和237 个现场试验，Malchaire[9]于2001 年对ISO 7933 中的典型Swreq（Required sweat rate）进行了改进，提出了修正后的指标——预测热应变模型（PHS），为PHS 热应力预测模型奠定了基础。Malchaire，Piette 和Ingvar[9-10]进一步将PHS 模型与WBGT（Wet Bulb Globe Temperature）指数进行比较，显示了PHS 模型在热应力预测方面的优势。此外，PHS 模型通过计算直肠温度和失水的限制，提供了一种预测最大允许暴露时间的方法[11-12]。许多强有力的验证对结果作出了贡献，使得PHS 模型已被采用在ISO 7933-2004 中，并一直广泛使用至今。

PHS 模型被广泛用于预测人体在极热环境中的热耐受时长，其理论基础是人体与环境间的热平衡方程。从热平衡方程角度来分析，影响人体散热的环境因素有：温差、水蒸气分压力差、辐射等，但是人体所穿着服装的服装热阻对传热同样有重要的影响。服装热阻作为PHS 模型中一个重要参数，对其计算的准确与否直接影响着PHS 模型最后的预测结果。

1.2 服装含水率对热阻的影响

服装热阻R 的定义为织物厚度与织物导热系数的比值：

式中：R 表示服装热阻，(m2·K)/W；h 表示织物的厚度，m；λ 表示织物的导热系数，W/(m·K)。

服装热阻是影响人体与环境换热的一个重要因素。大量学者的研究都证明了服装在润湿状态下的热阻往往小于干燥状态下的热阻[13-15]。干织物的热导率主要受其孔隙率的影响，织物孔隙度是由纱线细度、经纬纱排布结构参数决定的。另外一个关键因素就是织物中的水分。当服装在润湿状态下，水分子会取代织物空隙中的空气，由于水比空气具有更高的导热性，使得湿织物的热阻大大降低。水的导热系数是0.6 W/(m·K)，空气导热系数是0.024 W/(m·K)，水约是空气导热系数的25 倍[16]。

1.2.1 服装含水率定义

服装的含水率表示服装中含有的水分质量与湿态服装质量的比值，用MC（Moisture Content）表示：

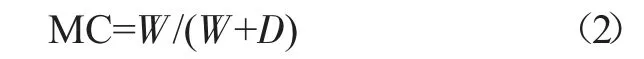
式中：W 表示服装中的含水量，g；D 表示服装在完全干燥状态下的质量，g。

与含水率类似用来表示服装的润湿程度的参数还有回潮率RE（Rate of Moisture Regain），表示材料中所含水分的质量与干燥材料质量的比值，表示为：

根据以上公式可以得到含水率与回潮率的关系为MC=RE/(RE+1)。众所周知空气中含有大量的水蒸气，当环境的温湿度不同时，水蒸气的含量会变化；而对于一般的织物而言，其含有的大量空隙就会吸收环境中的水蒸气并会放热冷凝使织物中存在一定量的水分，从而影响织物热特性改变其热阻大小。对于处在不同温湿度环境下的棉质纤维织物来说，其回潮率RE 可以大致用下面的公式表示[17]：

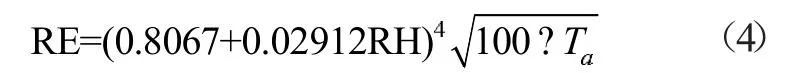
式中：RH 表示相对湿度，%；Ta表示环境温度，℃。

在PHS 模型中所使用的服装热阻Icl（clo），是在标准的测试环境下测量而来。因此根据式（4）及含水率和回潮率的关系得出，PHS 所使用的服装热阻是在含水率MC=0.075 状态下的热阻，并不是干燥热阻。

1.2.2 干燥服装质量

服装质量是计算含水率的重要参数，尤其是干燥状态下的服装质量。McCullough[18]利用暖体假人在气候控制室内测量了115 件不同服装和60 套具有代表性的经常在室内环境中穿着的套装的热阻值（clo）。采用回归分析方法，计算了服装热阻与服装质量的关系（皮尔逊相关系数R2=0.94）：

式中：AWT表示在测量环境下服装的质量，kg；Icl表示服装套装的热阻值，clo。

此时根据热阻计算得来的服装质量并不是干燥状态下的质量，根据上文所述服装中会含有一定量的水分，其含水率MC=0.075。对于大部分服装织物来说，当服装织物被水润湿后水分会浸润到服装织物间的孔隙当中，与服装形成类似于电路中的并联效果，据此我们假设服装与水分的热传导为并联模式，因此干燥状态下服装质量为：

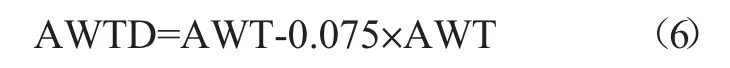
1.3 服装热阻修正系数

Evrim Kanat[19]使用ALAMBETA 测试仪测量了棉（CO），聚酯（PET），莫代尔（CMD）和丙烯酸（PAN）四种材质的面料在不同纱线支数下含水率分别为100%，75%，50%，25%以及绝对干燥状态下的热阻值，并采用回归分析的方法对四种面料进行了热阻的预测，预测方程包含纤维比热，纤维密度，织物厚度和回线密度等结构参数，成功预测了在不同含水率下的织物热阻。Chen[20]通过暖体假人测试了服装的隔热性能，分别模拟了暖体假人在低出汗量和高出汗量时测试服装的热阻，结果表明高出汗量下服装的隔热性能明显低于低出汗情况，原因是由于服装吸水后其隔热性能的降低。Wang[15]采用暖体假人，研究了服装合身性和含水率对服装湿式保温性能的影响。研究发现，含水率对保温损失有很大的影响并建立了三次多项式回归模型，定量分析了保温总损失与含水率之间的关系。研究还表明服装尺寸及合身程度对湿式保温效果影响最小。

需要建立的服装修正系数是直接将含水率与服装热阻建立联系，忽略服装面料纤维种类、纤维密度、纤维比热、厚度、孔隙率等因素。若将这些因素均考虑进去，会使PHS 模型更加复杂化，输入参数大大增加不便于使用与理解，因此需要一系列含水率与服装热阻关系的试验数据。Mangat[16-17，21]在2012 至2015 年做了一系列不同面料在不同含水率的情况下的湿态热阻变化。织物材质主要包括棉、聚丙烯（PP）、聚酯（PET）等，织物材质的主要参数如表1[16-17，21]所示：

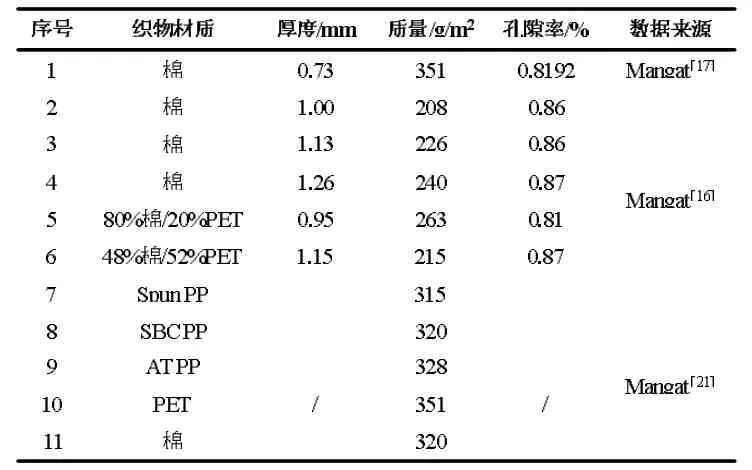
表1 试验织物的材质及各项参数

将M M Mangat 的试验数据进行综合分析，并进一步分析每组试验中织物热阻随含水率增加的下降比例，发现每组试验的热阻下降比例都遵循相同的趋势。在低含水率（MC＜0.3）时，热阻值的下降程度较大，热阻减少70%左右。当含水率进一步增大时（MC＞0.3）时，热阻值的下降趋势变得缓慢，说明少量的水分对织物热阻有显著的影响，进一步增加水量对热阻影响并不显著，如图1 所示。

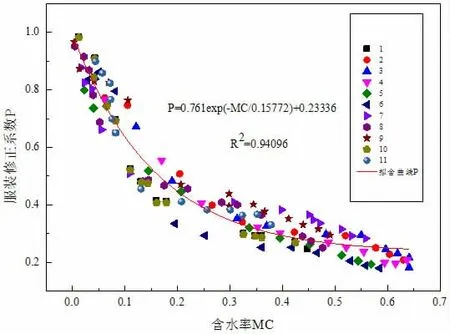
图1 服装修正系数P 随含水率变化关系

图1 中的试验数据一共涉及11 种不同织物，共140 个试验数据点。从散点数据随含水率变化的趋势来看，在织物含水率较低的情况下，热阻的下降趋势尤为明显。含水率在0～0.3 的范围内，热阻可下降70%左右，并且随着含水率的不断增加，热阻的下降趋势越来越平缓。当含水率大于0.3 时，这种热阻下降缓慢的趋势变得更加明显，热阻的下降幅度变得很小，随着含水率的继续增加，热阻的大小也基本不再变化。这表明在织物处于润湿状态下时，少量的水分是使其热阻降低的主要原因。

采用指数方程的形式去拟合采集的140 个试验数据点，最终的拟合曲线方程为：P=0.761e-MC/0.15772+0.23336，皮尔逊相关系数R2=0.94096，具有很高的相关性，因此可以使用方程来近似表示服装热阻随含水率变化的关系，当MC=0 时，P=1。本文将P 称之为服装热阻修正系数。

1.4 湿态热阻

1.4.1 服装含水率计算

如何确定当人体出汗时，服装的润湿程度即服装能够吸收多少出汗量是确定服装含水率的关键，也是计算润湿服装动态热阻的关键。由于服装的类型、面料、材质等均会影响其吸湿性能。此文中，假设工作人员穿着的服装都有良好的吸湿性能，且服装于人体皮肤处于紧贴的状态。当人体出汗时，服装吸收皮肤表面的汗液并于人体皮肤表面紧紧贴合，因此假设在这种状态下，服装能吸收人体出汗量的50%。因此，当工作人员处于一定的环境进行劳动时，由于出汗和环境温湿度的综合作用，服装的含水率MC 可以由下式计算得：

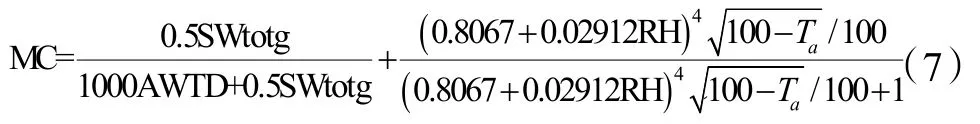
式中：SWtotg 表示出汗量，可由PHS 模型迭代计算得来，g；AWTD 表示干燥服装总量，kg；RH 表示相对湿度，%；Ta表示环境温度，℃。

1.4.2 动态湿态热阻

服装热阻在工作人员处于劳动的状态下并不是PHS 模型中所使用的一个不变的定值。由于环境温湿度、劳动强度等因素的影响，工作人员在劳动中不可避免地会出现大量出汗从而使服装润湿的情况。根据试验数据推导出了服装热阻随含水率变化的关系，即服装热阻修正系数P，则动态湿态服装热阻可上述计算公式推导计算出来，如下式：

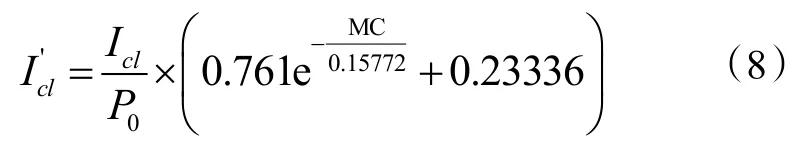
2 试验验证

将提出的动态湿态热阻应用到原PHS 模型中对其进行进一步的修正，修正后的模型称之为PHSW模型。为了验证PHSW模型对于热耐受时长的预测比之原PHS 模型的有效性，搜集了大量有关热耐受时长的试验数据，试验数据主要来自于陈颖，吕石磊及NA Pimental 等人[22-24]。由于不同人员的热耐受性不同，为了排除由于偶然性造成的误差，因此选择的试验数据至少是由4 个试验人员得出的平均值，试验结果与两模型的预测结果如图2～5 所示：

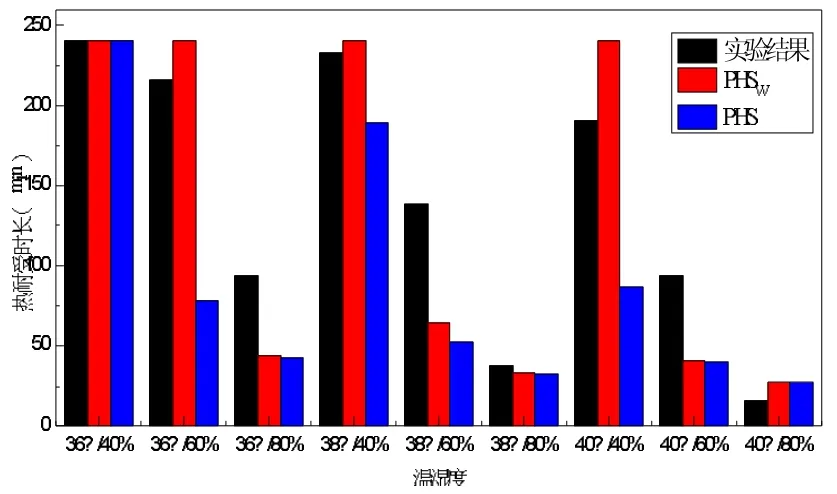
图2 热耐受时长试验结果[22]与PHSW、PHS 模型预测结果对比（核心温度达到38.5 ℃）

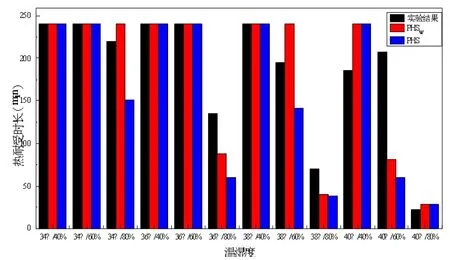
图3 热耐受时长试验结果[23]与PHSW、PHS 模型预测结果对比（核心温度达到39 ℃）

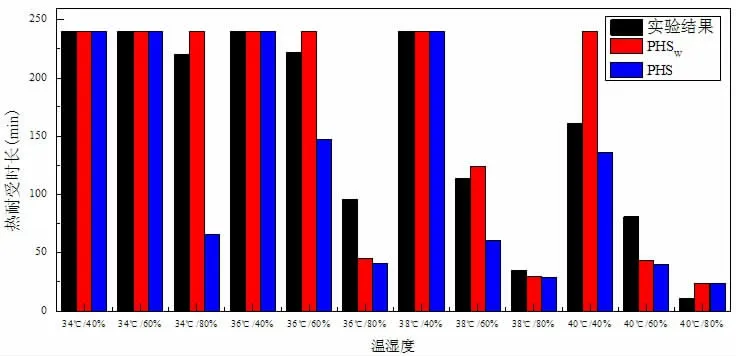
图4 热耐受时长试验结果[23]与PHSW、PHS 模型预测结果对比（核心温度达到38.5 ℃）

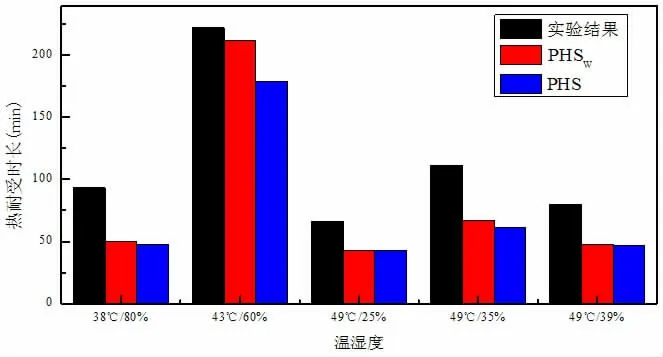
图5 热耐受时长试验结果[24]与PHSW、PHS 模型预测结果对比（核心温度达到39 ℃）

从图2～5 的对比结果来看，改进后的PHSW模型的预测结果比改进前更加的接近试验结果，但不是对于所有的环境条件改进效果都很明显。

根据图2 及图4，试验人员的退出试验的条件是核心的温度达到38.5 ℃。此时当相对湿度RH=80%时，处于很高的相对湿度状态下时，干球温度从34 ℃到40 ℃的模型改进前后预测结果的差别不大，只有很小的改进效果。当相对湿度RH=60%时，PHSW模型对于干球温度小于38 ℃的环境比原PHS 模型有更加准确的预测效果，在这种条件下原模型的预测结果远远低于真实的试验结果，而改进后的PHW模型对于这一状态的预测结果几乎和试验结果相同，证明了改进的PHSW模型具有更加可信的预测结果。当相对湿度RH=40%时，从图中可以看出在整个试验温度（34～40 ℃）范围内PHSW模型比PHS 模型都有更准确的预测结果。从上述结果可以看出，改进后的PHSW模型在低相对湿度及中等相对湿度情况下，对于干球温度小于38 ℃的环境的预测热耐受时长的准确度有明显的提高，而对高温（Ta≥38 ℃）及高湿度（RH≥80%）环境的预测结果改进并不明显。

根据图3 及图5，试验人员退出试验的条件是核心温度达到39 ℃以上。此时的结论与退出试验条件为核心温度达到38.5 ℃大致相同。特别从图5 中可以看出，在高温（Ta≥38 ℃）及高湿度（RH≥80%）环境下，改进后的PHSW模型的预测结果较原PHS 模型虽然有改进效果，但是效果不明显。

通过上述的试验数据，也可以明显看出空气温度和湿度对人体的热应激反应的影响。在不同的一系列试验中都表明在温度相同时，相对湿度越高人体在环境中的热耐受时长越短，并且当相对湿度大于60%后热耐受时长降低尤为明显，表明高湿度对人体热应激反应有尤为重要的影响。同样当相对湿度相同时，温度越高热耐受时长越短，并且相对湿度越大温度的影响效果也越明显。

3 结论

当人体劳动出汗时，服装热阻有由于服装的润湿而有所改变，并且随着服装润湿程度的不同，热阻的变化也会不同。本文对大量有关织物含水率对织物热阻影响的试验数据进行了整理分析，发现热阻随含水率的变化趋势都基本一致，在低含水率（0～0.3）的状态下，织物的热阻会出现明显的骤降，在此范围内热阻一般会降低70%左右。而随着含水率的不断升高，织物热阻的下降趋势明显减缓并趋于平缓状态，说明了织物的低含水率是造成其热阻降低的主要原因。应用回归分析的方法对大量数据进行了拟合求出了服装热阻修正系数P 的表达式并应用到PHS 模型中，得到改进后的PHSW模型。

针对人体在热环境下的热耐受时长的预测问题，将试验结果与改进前后的PHS 模型预测结果进行了对比分析。发现改进后的PHSW模型在低相对湿度及中等相对湿度情况下，对于干球温度小于38 ℃的环境的预测热耐受时长的准确度有明显的提高，而对高温（Ta≥38 ℃）及高湿度（RH≥80%）环境的预测结果改进并不明显。