毛细非饱和多孔介质液气相变传质特性数值模拟

杨牧沄 吴晋禄 黄洁洁 高峄涵 高乃平

1 同济大学机械与能源工程学院

2 上海新型烟草制品研究院有限公司

多孔介质是指由固体骨架和其构成的孔隙空间所组成的一类复合介质。与孔隙内只有气或液一相存在的饱和多孔介质不同，非饱和多孔介质孔隙内同时存在气液两相，其应用广泛存在于食品干燥、热泵系统、岩土工程、建筑材料、烟草制品等领域，其研究往往涉及两相流动，毛细压力，流体相变和非线性孔隙空间等复杂机理。在不同的研究背景下，大量学者的研究内容往往具有不同的研究重点。王刚等[1]采用数值模拟与实验相结合的方法，基于多孔介质模型研究了蒸发器内部速度，温度和压力分布，提出风道结构的优化方向。Talih 等[2]建立了受热多孔雾化芯的集总参数模型，得到加热功率，液体组成和运行参数对特定成分通量的影响规律。Ha 等[3]采用动力学方法，建立了多孔纤维素在电加热器内的蒸发热解的二维瞬态模型，数值模拟结果与经典模型相比显示模型具有优势。在现有文献中，少见对非饱和多孔介质内发生的毛细输运和相变传质相耦合的研究。因此，本文以非饱和多孔介质为研究对象，考虑介质的毛细输运能力对孔隙内液气相变传质的影响，建立了毛细输运与相变传质耦合计算的数值模型，基于Matlab 软件模拟并讨论了不同加热功率，液体组成和孔隙率下的非饱和多孔介质传质特性。

1 数值模型

1.1 模型介绍

本文所研究的柱形多孔介质总长L，直径D。介质中央部分区域外有电热丝缠绕（加热区），加热区长度为Lh，电热丝功率可控。作为液气相变出口的柱形气流通道与介质中央垂直相交，通道直径同样为Lh，其中的空气流速固定。多孔介质事先被液体工质浸润，液体工质组成为纯丙二醇（PG），纯丙三醇（VG）以及两者按1:1 体积比混合的溶液。当孔隙内的液体被气化时，外部的液体工质从多孔介质两端通过毛细作用自发向内输运填充。为了确定多孔介质的液体毛细输运能力的极限，需要进一步研究工质的轴向流动过程。由于物理模型的几何结构存在对称性，取多孔介质无电热丝缠绕区域（输运区）的一端进行建模分析，模型示意图如图1 所示。

图1 数值模型示意图

图1 中：Lt为多孔介质输运区一端长度，m；x 为所取微元体与加热区边界的轴向距离，m；h(x)为所取微元体视为液相连续体的液面高度，m；u 为液体毛细输运速度，m/s；为单位距离上的液体气化质量速率，kg/(m·s)，加热区的液体气化简化视为轴向平均分布；为单位距离上的液体输运质量速率，kg/(m·s)。

1.2 控制方程

为便于计算，采用多孔介质连续介质假设和局部热平衡假设[4]，多孔介质视为刚性骨架，内部孔隙均与外界环境连通且均匀分布，液相按不可压缩流动处理，气相按饱和理想气体处理，各相均为各向同性且采用常物性参数。

提取微元体进行连续性分析，相应的质量守恒方程为：

式中：ρl为液体密度，kg/m3，混合液的密度取为各组分密度以组分质量分数乘积加权作和，其他混合参数的计算方法类似。

非饱和多孔介质中液体的毛细流动满足达西定律[6]，即流动驱动力为液体流动方向前后压差，相应的动量方程表示为：

式中：μl为液体动力粘度，N·s/m2；pl为孔隙内液体压力，Pa；K 为多孔介质渗透率，m2。基于Kozeny[7]和Carman[8]的研究，多孔介质渗透率与孔隙率、平均孔隙半径rave和孔道弯曲因子τ 之间存在关联式为：

而根据毛细压力的定义，毛细压力pc可表示为气相压力pg和液相压力pl的压力差。由于毛细压力在这里提供液体流动的驱动力，而气相压力与外界气压相等，因此多孔介质内毛细输运流动的动量方程可化为：

对于同一多孔介质，毛细压力可以通过Leverett提出的无因次函数J(s)与饱和度相关联[9]，毛细压力的饱和度关联式为：

式中：σ 为气液表面张力，N/m。

忽略残余饱和度，无因次函数采用Udell[10]提出的经验式为：

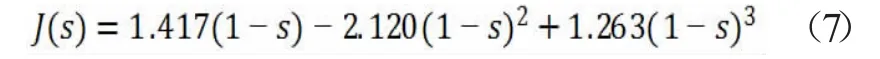
2 模拟条件及求解方法

2.1 边界条件

1）多孔介质的液体毛细输运入口处的具体边界条件为：

2）多孔介质的液体毛细输运出口同时也是液体发生受热相变的地方，此处边界条件应满足：

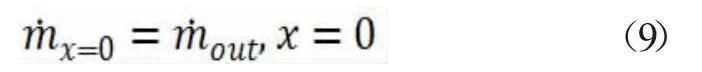
液体的毛细输运质量速率可由式（3）代入下式可得到：

式中：hD为多孔介质表面液体对流传质系数，m/s；ρg为液体蒸发产生的气体密度，kg/m3；As为多孔介质表面对流传质面积，m2；为液体汽化潜热耗热率，W；hfg为单位质量液体汽化潜热，J/kg；T 为液体温度，℃；Tb为沸点温度，℃。

液体在多孔介质加热区内发生气化换热过程，液体升温和气化的能量来自于电热丝输入能量中排除热损失的剩余部分，其中热损失包括湿介质与绕流空气的对流换热损失，湿介质的轴向导热损失以及辐射损失。因此根据能量守恒方程有：

2.2 求解方法

采用Matlab 作为计算软件，对上述控制方程采用有限差分法进行离散，毛细输运过程的求解采用二阶中心差分格式，液气相变过程的求解采用一阶前向差分格式[2]。液体质量速率的计算精度为0.0001。为了确定多孔介质毛细输运极限，即通过毛细作用可输运的最大液体质量速率，经过验算将处于毛细输运极限下多孔介质内饱和度最低值设定为30%。多孔介质直径3 mm，轴长16 mm，其中加热区长度为8 mm，输运区一端长度为4 mm。气流通道直径8 mm，空气流速0.36 m/s。多孔介质孔隙率实测平均值为44%，平均孔隙半径为100，孔道弯曲因子为1。介质固体骨架密度为500 kg/m3，比热容为1275 J/(kg·K)，轴向热导率0.049 W/(m·K)。介质表面与绕流空气的对流换热系数8.5 W/(m2·K)，介质辐射系数为5.67×10-8W/(m2·K4)。加热时长同时也是模拟总时长为3 s。介质和液体的初始温度以及环境温度均为10 ℃。数值模拟采用的液体物性参数如表1 所示。

表1 数值模拟采用的物性参数

3 计算结果及分析

为了验证数值模型的准确性，对五组不同加热功率（1.36～9.09 W）下的三种液态工质（PG，VG，PG 和VG 以1:1 体积比混合）的模拟结果与实验结果[11]进行对比，计算条件均与实验条件相同。一定加热功率下平均气化质量速率的模拟与实验结果对比如图2 所示。图2 中两种模拟结果的差异在于是否有考虑毛细输运极限对相变传质的限制作用。模拟I 为不考虑毛细输运限制的模拟结果，模拟II 为考虑毛细输运限制的模拟结果。由图2 可知，当加热功率小于6 W 时，两种模型的结果相差不大，而当加热功率大于6 W 时，考虑毛细输运限制的计算值与实测值更为吻合，而不考虑毛细输运限制的模型计算值要远大于实测值，说明较高加热功率下，多孔介质内的液气相变传质受到毛细输运极限的限制，且这种影响不可忽略。因此，考虑毛细输运限制的数值模型计算相比更为复杂，也更能准确反映真实物理情况。但当加热功率小于6 W时，采用不考虑毛细输运限制的数值模型能减少计算量，同时不影响结果的准确性。

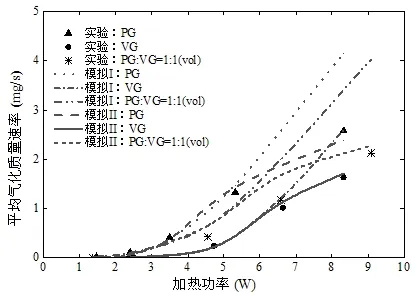
图2 三种液体平均气化质量速率与加热功率的关系

基于已验证的数值模型，对不同加热功率和液态工质组成下，液体平均气化质量速率与介质孔隙率的关系进行研究，结果如图3 所示。由图可知，当加热功率和介质孔隙率不变时，对比PG-VG 双组分液体工质的不同组成情况，其中纯丙二醇的液态工质具有相对最高的平均气化质量速率。这是由于液气相变过程由于液体温度和气化状态不同，分为蒸发和沸腾两个阶段。而同时相比丙三醇，丙二醇具有较高的对流传质系数和较低的汽化潜热，因而在整个液气相变过程中都能体现出更强的传质特性。

图3 不同加热功率下平均气化质量速率与孔隙率和液体组成的关系

此外，由图3 还可知，当加热功率和液态工质组成不变时，存在最佳的介质孔隙率，使得该介质孔隙率下液体平均气化质量速率处于极大值，即此时多孔介质传质性能最好。最佳孔隙率的取值与加热功率有关，且随着加热功率增大而升高。加热功率从1.36 W增加到9.09 W，对应最佳孔隙率从0.3 增加到0.7。最佳孔隙率与液态工质组成无明显关系。对于不同液态工质，当加热功率相同时，最佳孔隙率基本一致。因此根据加热功率选取特定的介质孔隙率有助于发挥出非饱和多孔介质的最佳传质性能。

之所以存在图3 中最佳介质孔隙率的原因，一方面是液气相变传质与液体温度相关，而增大孔隙率会增加湿多孔介质里液体的比重，从而加大导热损失，造成同样条件下液体升温减慢，液气相变传质减少。另一方面，介质对液体的毛细输运能力极限可能与介质参数和液体组成有关。为了研究不同因素对介质毛细输运能力极限的影响，对不同孔隙率和液态工质组成下液体毛细输运极限质量速率进行模拟，结果如图4所示。由图可知，非饱和多孔介质的毛细输运能力极限仅和介质孔隙率组成有关，与液体组成和加热功率基本无关。主要原因是在孔隙视为均匀分布的假设下，孔隙率增大即意味着孔隙数量增多，因而多孔介质的毛细输运能力的极限也随之上升。除此之外，由控制方程可知液体毛细输运极限质量速率还与液气表面张力和液体动力粘度有关，但其影响作用方向相反。因此对于所研究的PG-VG 双组分液态工质，液体毛细输运极限质量速率与液态工质组成关系不大。对于其他工质可能会有不同结论。

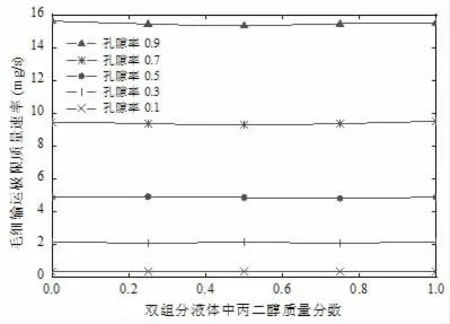
图4 毛细输运极限速率与介质孔隙率和液体组成的关系

4 结论

本文考虑了介质对液体存在的毛细输运极限对液气相变的限制作用，建立了柱形多孔介质内双组分液体毛细输运-受热相变过程的数值模型，通过与实验数据比较验证了模型的准确性，研究了加热功率、液态工质组成、介质孔隙率三种因素对非饱和多孔介质传质性能的影响。研究结论如下：

1）非饱和多孔介质的传质性能由相变传质和介质毛细输运极限共同决定。介质毛细输运极限决定了多孔介质传质性能的上限，且主要与孔隙率有关。随着孔隙率增加，液体毛细输运极限质量速率逐渐增大。加热功率和液体组成主要影响多孔介质的液气相变传质。加热功率越高，液体气化越多，则多孔介质传质特性越趋近其上限。

2）当加热功率较低时（本研究中临界功率为6 W），采用不考虑毛细输运限制的数值模型能减少多孔介质毛细输运-受热相变过程传质的计算量，同时不影响模拟结果的准确性。但当加热功率较高时，多孔介质内的液气相变传质可能会受到毛细输运极限的限制，且这种影响不可忽略，不考虑毛细输运限制的计算会存在较大偏差。

3）当加热功率和液体组成不变时，对于几何尺寸固定的多孔介质存在最佳的介质孔隙率，使得多孔介质传质性能最好。最佳孔隙率的取值与加热功率有关，与液体组成关系不大。当加热功率从1.36 W 增加到9.09 W 时，对应最佳孔隙率从0.3 升高至0.7。