基于频谱分析用针刺仪测定树木年龄的算法

潘 虹，卢 军，郭旭展，唐守正，高瑞东，徐建军

(1.中国林业科学研究院资源信息研究所，北京 100091；2.信阳师范学院数学与统计学院，河南 信阳 464000；3.管涔山国有林管理局，山西 宁武 036700；4.管涔山国有林管理局羊圈沟林场，山西 五寨 036200)

活立木年龄微损测定是目前林业生产研究中最重要和最基础的共性难题，对森林管护、森林经营以及古树保护等都具有重要的理论和实践意义[1-4]。传统的测定树木年龄的方法具有破坏性[5-6]，并增加树木致病感染的风险[7-10]；无损测定树木年龄的方法如建立数学模型和查数轮生枝法等[11-15]，准确性较低。目前，在我国实行天然林保护的环境中，亟需一种微损的测定树木年龄的方法。

针刺仪是估计树木年龄的微损工具，将针刺仪应用于活立木，可以获得相对阻力剖面[16]。针刺仪的基本工作原理是基于抗钻阻力与木材密度之间的线性关系，根据剖面曲线波峰波谷的趋势能反映年轮内部早材和晚材的界限[17]，峰值和谷值分别代表早材和晚材，可以用相对阻力剖面图来估计树木年龄以及树木生长率[18-20]，由于针叶树和阔叶树的树干材质不同，导致针刺仪钻入阻力变化不同，针叶树种的阻力变化比阔叶树种的阻力变化更明显，峰谷的区分度更好，能更准确地表示树木生长的变化，所以本研究选取针叶树中的华北落叶松（Larix principis-rupprechtiiMayr）作为研究对象。虽然使用针刺仪自带DECOM 软件对抗钻阻力剖面图进行分析，可以自动检测年轮边界，估计树木年龄，但是误差很大，不能应用于林业实际生产，基于抗钻阻力值序列来估算树木年龄的方法鲜见报道。

数字信号处理是将复杂的信号用简单的基本的信号表示，从而将复杂的信号分析转化成对基本信号的分析[21]。已经实际应用于广泛的学科领域，如语音处理、电话信道传输、图像处理和传输等[22-23]。傅里叶变换是数字信号频域分析的一种重要方法，可以将时域的信号用虚指数信号表示，反映了信号的时域与频域之间的关系[24-25]，是信号分析中不可或缺的重要工具，在各个领域都有广泛应用[26-27]。

针刺仪钻入活立木获取的抗钻阻力值序列，可以看做离散周期信号，从而可以考虑利用数字信号处理对其进行分析，来寻找树木年度变化的信息。本研究以德国RINNTECH 公司生产的树木针刺仪（Resistograph 4452P/S）钻入华北落叶松获取的抗钻阻力值序列为研究对象，利用数字信号处理中的傅里叶变换，对抗钻阻力值序列进行离散谱分解，通过确定代表树木年龄变化的谐波的周期数来估计树木的年龄。

1 样品采集

2017 年10 月，在山西省羊圈沟林场的华北落叶松人工林中，按径阶大、中、小至少各选3 株，优势木各选2 株，共52 株样木进行针刺试验。用针刺仪在每株样木胸径1.3 m 处4 个方向钻入，获取有效抗钻阻力值序列208 组。2018 年6 月，在相同的样木上，使用针刺仪在距离地面0.2 m 处和0.5 m 处分别从两个不同方向钻入，获取有效抗钻阻力数据115 组，两次试验共获取有效抗钻阻力数据323 组作为研究对象。

最后将样木伐倒，在树干上标明南北向，并分别在0.2 m、0.5 m 和1.3 m 针刺位置5 cm 内截取圆盘，在圆盘非工作面上标明南北方向，并以分式形式注记，分子为样地号和解析木号，分母为圆盘号和断面高度，共获取有效圆盘104 个。对圆盘进行抛光，打磨，扫描，用WinDENDRO 年轮分析系统结合人工判读方式获取圆盘年轮数，圆盘的年龄分布和径阶分布见表1 和表2。

表1 圆盘年龄分布汇总Table 1 Summery of disc age distribution

表2 圆盘径阶分布汇总Table 2 Summeryof disc radial distribution

2 利用频谱分析测定树木年龄的原理与方法

2.1 频谱分析原理

假设每年生长近似相同，针刺仪钻入活立木获取的相对阻力剖面记录为时间序列z={z1,z2,···,zk,···,zn}，n为针刺仪测量点的序列号，假设时间间隔为δ，则序列z是总时间长度为T=nδ的离散周期信号，以下将针刺仪抗钻阻力序列称为离散周期信号z。

离散时间信号z中 包含3 个部分的信息：趋势、年度变化、噪音。利用频谱分析估计树木年龄的基本思路：将离散时间信号z去趋势后，进行谱分析，确定代表年度变化的谐波信息。根据傅里叶分析可知，在时间T上，信号z可以分解成各种频率三角函数的和，由于树木生长1 年对应1 个峰，1 个周期内有1 个峰，估计树木的年龄取决于峰的数量，峰值和谷值分别代表早材和晚材。所以在这些三角函数中找到代表年度变化的周期数f，也就确定了周期P和年龄A，周期P在本研究中是指树木生长1 年所对应的抗钻阻力值序列长度，即由T=PA,T=f A，可得P=f。因次，估计树木年龄关键是确定代表年度变化的周期数。

2.2 利用频谱分析估计树木年龄的方法

估计树木年龄的基本思想是将抗钻阻力序列利用平滑器去趋势，然后再用傅里叶变换做频谱分析，给出k次谐波的系数，求出k次谐波的振幅，树木的年龄规律在振幅较大的谐波中得以体现。设定振幅比ε，寻找与最大振幅比值大于ε的振幅所对应的k次谐波的周期数k。

2.2.1 Savitzky-Golay 平滑器 Savitzky A 和Golay M 在1964 年提出了一种基于多项式拟合的方法来设计的形式简单的滤波器[20]，对抗钻阻力值所组成的离散周期信号z，把其中任一段数据测量点位置记为向量m=−M,···,0,···,M，测量点处对应的数据用一个p阶多项式拟合：

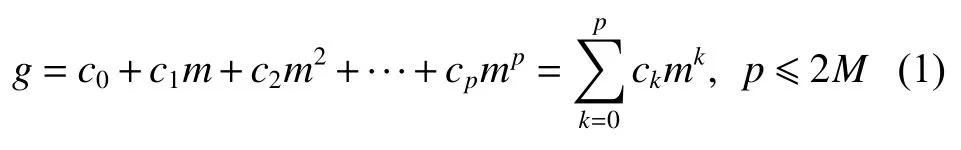
共有2M+1点数据，多项式拟合阶数为p，这种滤波器称为Savitzky-Golay 平滑器，该平滑器允许窗长可以较大，且对于大部分数据的平滑都比较有效。使用该平滑滤波器对信号z滤波，可以求取趋势项，用信号z减去趋势项，就得到所期望的去趋势后的信号，记为x={x0,x1,···,xk,···,xn−1}。

2.2.2 傅里叶级数与傅里叶变换 利用离散傅里叶级数，实现抗钻阻力序列经过去趋势后所得到的新的序列x从时域到频域的映射，利用离散的傅里叶变换，将长度为n的 时域序列x表示成n项虚指数信号的加权和，从而反映离散时间信号x中不同谐波分量的分布规律。

离散时间信号x的 离散傅里叶级数系数表示为：

离散时间信号x的逆离散傅里叶级数系数表示为：

2.2.3 离散时间信号的频谱分析 针刺仪获取的抗钻阻力值序列z经过去趋势后得到离散周期信号x，记为：

其谐波分解（谱分解）表示为

系数的估计公式为：

当n=2q+1时，q=r，上面3 个估计系数的等式成立。

当n=2q时，r=q−1对于前q−1项系数，即k

用离散傅里叶级数系数表示离散谱分解系数，估计公式为：

用逆离散傅里叶级数系数表示离散谱分解系数，估计公式为：

记：α=(α1,α2,···,αq)，其中αi=Re(bi),i=1,2,···,q；β=(β1,β2,···,βq)，其中βi=Re(bi),i=1,2,···,q。

将第k谐波的振幅记为Mk，即

谐波周期数为k，说明波峰出现的次数为k。若代表年龄变换为第k次谐波，则树木的估计年龄为谐波的次数k。将所有谐波的振幅及对应的周期数用矩阵表示：

矩阵P的每一行表示振幅和对应的周期数。

将向量M1和N1作为矩阵P1的第一列和第二列，即

将向量M2和N2作为矩阵P2的第一列和第二列，即

则矩阵P2是由矩阵P1的前j行组成，向量N2是与最大振幅比大于ε的所有的振幅按照从大到小排列组成。向量M2是每个振幅所对应的周期数。

将向量M2中所有分量取均值，记为δ，即

则δ表示树木的年龄估计值。频谱分析估计树木年龄的流程图（图1）：

图1 频谱分析估计树木年龄流程Fig.1 Flow chart of tree age estimation by spectrum analysis

2.2.4 步骤输入：针刺仪钻入活立木获取的相对阻力值序列z={z1,z2,···,zk,···,zn}。

step1 给定窗口大小Wid，将针刺仪获取的抗钻阻力序列z为离散时间信号，经过Savitzky-Golay平滑器，进行去趋势后得到离散时间信号x。

step2 利用公式（3）求出逆傅里叶变换求出离散时间信号x的逆傅里叶级数系数。

step3 利用公式（11）求出离散时间信号x的谐波分解系数。

step4 求出所有谐波的振幅，并按照从大到小进行排列，与所对应的谐波的周期数作为行向量写入矩阵P1。

step5 给定振幅比ε=0.85，将所有与最大振幅比值大于ε的振幅以及对应的周期数作为行写入矩阵P2。

step6 求出矩阵P2的第一列向量的均值δ，作为树木年龄的估计值。

输出：树木年龄估计值δ。

以上过程通过MATLAB 编程实现。

3 结果

对104 个圆盘所对应的抗钻阻力值序列进行频谱分析，首先根据圆盘直径大小，选择相应窗口值Wid，如表3 所示，对原始抗钻阻力值序列进行去趋势得到相应的离散周期信号，然后对其进行离散谱分析，计算得到所有谐波的振幅，将所有的振幅与对应的周期数作图可以看出全频谱分布情况，设定振幅比为0.85，求出与最大振幅比大于0.85的所有振幅都对应的周期数。以数据1 699 为例，数据1 699 是使用针刺仪在落叶松6 胸径处获取的数据，其胸径为14.7 cm，设定相应窗口为501，进行去趋势获取相应的离散时间信号记为x1699，对x1699进行离散谱分析，可以得到所有谐波的振幅，谐波次数与对应振幅做直方图可以看出全频谱分布情况，见图2。设定振幅比为0.85 后，计算出该数据第49 次谐波所对应的振幅满足条件，说明第49 次谐波的周期变化代表树木年龄变化，因第49 次谐波所对应的周期数为49，从而可以将周期数的一半作为该株落叶松胸径处的估计年龄，为24.5 a，实测年龄为25 a，精度较好。

表3 参数Wid 选择依据Table 3 The selection basis of parameter Wid

图2 数据编号1 699 频谱分析过程Fig.2 Spectrum analysis process of 1 699 data number

根据每个圆盘的直径选择相应的窗口大小，对原始抗钻阻力值序列去趋势后进行离散谱分析，可以得到每组抗钻阻力值所对应的的周期数的平均数δ，试验过程中，每个圆盘针刺获取的抗钻阻力值为2 组或者4 组，将对应的2 组或者4 组值的频谱分析结果取均值，作为圆盘的频谱分析算法估计年龄，所有圆盘频谱分析算法估计年龄与实测年龄对比见图3。

图3 频谱分析算法估计年龄与DECOM判定年龄对比Fig.3 Comparisons of age estimation by spectrum analysis algorithms and DECOM judgment test

每个圆盘的频谱分析算法估计年龄与实测年龄的相对误差分布见图4，针刺仪自带软件DECOM自动判读年龄结果误差较大，误差范围是−25 a 至2 a 之间，平均误差是−12 a，相对误差大多集中在−20%至−60%之间，最小相对误差为−7.69%，最大相对误差达到−84.78%，平均相对误差达到−49.98%。圆盘的实测年龄范围是18～27 a，频谱分析算法估计年龄误差范围是−5～6 a 之间，平均误差是−0.25 a，平均绝对误差是2 a；相对误差分布大多集中在−10%至10%之间，最小相对误差为0，最大相对误差为25.69%，平均相对误差为−0.35%。

图4 频谱分析算法估计年龄与DECOM 判定年龄绝对误差分布Fig.4 Relative error distribution map of age estimation by spectrum analysis algorithms and DECOM judgment test

分别对真实年龄与软件自动判别年龄（第1对）、真实年龄与算法估计年龄（第2 对）进行成对数据t 检验。第一对数据检验得到的t值为20.25，给定显著性水平δ=0.05，查表可得t1−δ/2(n−1)=t0.975(9)=2.262 2，由于 |t|>2.262 2，故拒绝原假设，即可视为DECOM 判定树木年龄均值与真实年龄均值之间有显著差异，此时检验的p值为2.2 × 10−6。第二对数据检验得到t值为0.85，由于|t|<2.262 2，故不能拒绝原假设，说明频谱分析算法估计树木的年龄均值与树木的真实年龄均值无显著差异，此时检验的p值为0.394 9。

4 结论

通过给出的频谱分析算法，将针刺仪获取的华北落叶松抗钻阻力值序列作为输入，根据树木的径阶给定窗口参数后，可得出活立木年龄的估计值，且精度较好，提高了针刺仪测定华北落叶松年龄的精度，改进了针刺仪自带DECOM 软件识别树木年轮边界准确率低，过于依赖人工经验的缺点，可以作为一种微损的估计华北落叶松年龄的有效方法，为活立木年龄的微损测定开辟了新的途径。