考虑导引头视场角的仿生分段复合制导律研究

王正杰， 蔡长青， 黄伟林

(北京理工大学 机电学院，北京 100081)

未来单兵作战武器的多样化、数字化和智能化是必然的趋势. 从单兵对小型化无人机的需求出发，研制出尺寸较小、质量较轻，便于单兵携带能够根据作战目的进入指定空域完成自主飞行侦查或攻击任务的微小型弹药是各国军事力量发展的重点之一，美、法、以色列、俄罗斯、乌克兰等国先后投入大量科研力量研制[1].

在军事领域，单兵便携式的小型弹药的潜能越来越凸显，主要体现在体积小而轻、操作简捷而迅速、准确侦查或打击、隐蔽性好以及价格低廉等优势[2]，从另一个角度来说，也正是由于体积小、质量轻等特点，微小型弹药大多安装了捷联成像导引头来进行目标探测，导引头探测范围受弹体动力学影响探测视角也会大大受限. 另外，采用传统制导律导引弹药去拦截迎面而来的目标，较大的相对速度会导致弹药末段需用过载大，弹目视线角速率过早发散，捷联体制的导引头会发生丢失目标等问题[3]. 针对低成本微小型弹药的精准攻击需求，需要提出一种具有针对性的新型制导律.

目前国内外针对导引头视场角受限的制导律研究很多，其处理方法主要分为两类，一类是设计一种保持目标视差角(目标偏离导引头视场中心的角度)定常的制导律，在制导过程中目标快要超出导引头视场范围时便切换至此制导律以保证目标始终位于导引头视场范围内. 比如，Sang D K等[4]针对固定目标，设计了一种攻击时间可控的导引律和目标视差角定常的制导律，在制导过程中让这两种制导律满足一定的切换逻辑，使得目标不会逃逸出导引头视场. 林鹏等[5-6]则针对微小型飞行器捷联制导问题，设计了一种比例滑模混合制导律，比例导引为传统的比例导引，滑模制导律的滑模面选取的是目标视差角，用于控制目标始终位于导引头视场内，在整个制导过程中让弹药在比例导引与滑模制导方式之间切换，使得目标不会逃离出导引头视场. 两种不同导引律直接切换可能会造成切换点处导引指令的过大跳变，从而影响制导性能和命中精度. 另一类则是直接分析整个制导过程中目标的最大视角，通过限制弹药的运动状态或者为制导律增加偏置项来达成目标的视差角不超出导引头视场的目的. 张道驰等针对固定目标的大落角攻击问题，分析了最优弹道成型制导律下导引头的最大目标视差角，通过选择适当的初始弹目视线角或者约束弹药的最大落角来使目标始终处于导引头视场角内[7]. 席杰等针对固定目标的大落角攻击问题，在带落角约束的最优制导律的基础上，设计了具有目标视差角修正能力的偏置项加入原有制导律，以保证目标始终处于导引头视场中[8]. 以上处理方法多是针对固定目标，对于运动目标的导引头视场角受限的制导问题，相关研究文献比较少.

昆虫学家发现，蜻蜓主要依靠光流感知外界环境变化与探测目标[9]，因此飞行昆虫在追踪目标时，可以使自身一直保持在焦点和目标连线上，从而使目标的视网膜中不能形成自己的光流，于是便让目标以为自身一直保持在焦点不动，进而可以对目标进行快速准确而又隐蔽的捕捉. 焦点为蜻蜓选取的伪装背景，它可以是实际的不动景物，也可以是一个不动的虚拟点，它可以位于有限远，也可以位于无限远. 生物这种隐蔽的飞行策略被称作为运动伪装(motion camouflage)[10-11]. 随后，美国研究人员记录了蜻蜓捕食的全过程[12-13]，用高速摄影记录蜻蜓的捕食轨迹. 在对大量轨迹进行研究后发现，蜻蜓在捕食果蝇前会使自身静止在某一处地方以搜索潜在的目标，当它发现目标的距离，飞行方向，飞行速度等参数合适时便会起飞开始捕捉目标，并且在短时间内快速扭转自身身体，使自身身体轴线在水平面内大致与果蝇飞行方向一致，在铅垂平面内与果蝇飞行方向呈一个比较小的夹角，此后则运用运动伪装追踪策略追踪目标，以保证蜻蜓在整个捕食跟踪过程中不易丢失目标果蝇. 特别是针对追捕迎面目标时，蜻蜓会通过调整自身姿态，保持以尾追模式追捕目标，并在追踪后半段使用与目标不产生相对角运动的运动伪装的追踪策略捕捉目标. 这种策略，可以确保蜻蜓在追捕目标末段，目标时刻在蜻蜓视场内，同时飞行轨迹平直，需要的加速度更小. 动伪装追捕方法也便于蜻蜓隐藏自身运动.

本文提出基于生物灵感的仿生制导律. 制定分段制导策略，末制导初始段，利用滑模控制律调整弹目视差角，控制弹药以尾追姿态攻击目标，末制导最后攻击段，运用焦点位于无限远的运动伪装制导律进行目标跟踪，保证弹道平直需要法向过载最小. 其中，末制导初始段与攻击段采取2阶平滑交接控制律进行过渡.

1 数学模型与问题描述

为了方便研究空间制导弹目交会问题，作如下假设以简化3维运动模型：①将3维的空间制导问题分解至横纵向平面，转化为2维平面问题； ②在末制导过程中弹药速度大小不变.

以铅垂平面为例，如图1所示，M为弹药，T为目标，F为平面内任意选取的一个固定点，定义为焦点，r为弹目距离，rm为弹药到焦点的距离，vm和vt分别为弹药和目标的速度，q为弹目视线角，qm为弹药相对于焦点转过的角度，θm和θt分别为弹药和目标的速度方向角，α为攻角，ψm为弹体姿态角，ηt为目标前置角. 定义弹药纵轴与弹目视线的夹角为视差角，即ηm.

图1 迎击拦截状态时弹目相对运动示意图Fig.1 Relative motion diagram of missile and target in the state of intercepting

弹药相对于焦点的运动方程为

(1)

弹目相对运动方程可以表示为

(2)

目标前置角ηt和视差角ηm可以表示为

(3)

通过目标前置角的绝对值进行追踪姿态判定[14]：

|ηt|<90°，则弹药处于尾追目标状态；

|ηt|>90°，则弹药处于迎击目标状态.

2 仿生制导策略设计

2.1 初始段制导律设计

初制导段的目的是使弹体像蜻蜓一样，快速调整自身的姿态，由迎击目标转为尾追目标的运动状态. 蜻蜓由于自身的身体特性可以大幅度扭转自身的身体以达到快速调整自身姿态的目的，但弹药的动力特性没办法使他与蜻蜓的姿态调整方式类似. 考虑到弹药的飞行动力学特性和探测目标的视场角限制，这里运用控制目标视差角方式的滑模原理来设计李雅普洛夫函数为

(4)

求导得

(5)

令

(6)

(7)

此时

(8)

于是得到初始段制导律为

ny=am/g+cosψm=

(9)

2.2 基于“运动伪装”的末段制导律设计

飞行昆虫在追踪目标时，可以使自身一直保持在焦点和目标连线上，从而使目标的视网膜中不能形成自己的光流，于是便让目标以为自身一直保持在焦点不动，进而可以对目标进行快速准确而又隐蔽的捕捉，焦点可以位于有限远，也可以位于无限远[10]. 生物这种“运动伪装”的追踪轨迹不仅能够隐蔽自身的行动，较平直的路径也降低了跟踪难度，因此制导末段可以仿照这种方法去设计制导律.

图2为焦点位于有限远时“运动伪装”弹目相对运动时的情况，F为焦点，M为弹药，T为目标，FT为伪装线. 图3为焦点位于无限远时“运动伪装”弹目相对运动时的情况，其中弹药初始位于M0，目标初始位于T0，q0为初始弹目视线角. 由于弹药在末制导阶段速度大小保持不变，即弹药切向过载为0，于是末段制导律的就是求取弹药的法向过载，使得弹药一直保持在伪装线上.

对于图2这种情况，弹药偏离伪装线的程度可以用直线FM和直线MT的夹角表示，即误差角er，为

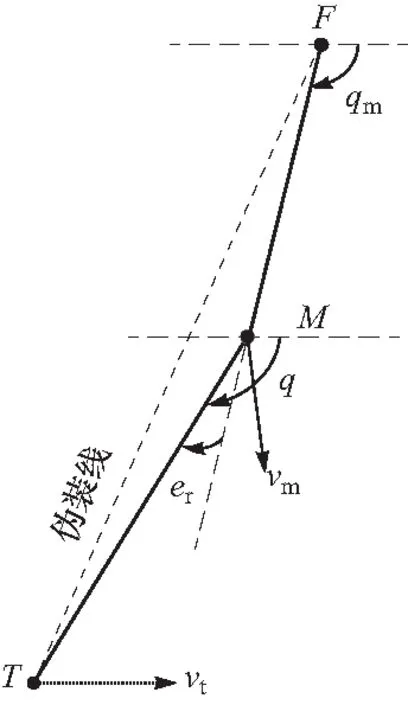
图2 焦点位于有限远时“运动伪装”弹目相对运动示意图Fig.2 Relative motion diagram of motion camouflage with fixed point at finite place

er=q-qm

(10)

对于图3的情况，误差角为当前弹目视线角q与初始弹目视线角之差,

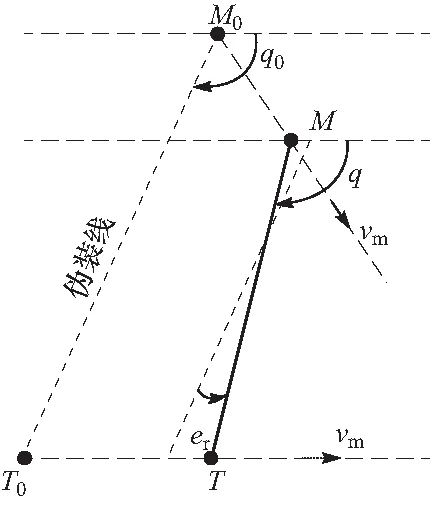
图3 焦点位于无限远时“运动伪装”弹目相对运动示意图Fig.3 Relative motion diagram of motion camouflage with fixed point at infinite place

er=q-q0

(11)

由于焦点位于无限远的运动伪装追踪轨迹弹道更为平直，需用法向过载更小，因此本文主要采用这种情况下的运动伪装仿生制导，此时设计制导律就相当于设计闭环的控制律，通过控制弹药速度方向，使得误差角er趋于0. 这里选用PID控制律，即

(12)

式中：Kp，Ki，Kd分别为PID比例，积分，微分参数；t为制导时间，于是基于“运动伪装”的末段仿生制导律为

(13)

2.3 过渡段制导律设计

初末制导段之间的切换阶段制导律主要针对两个问题：初末制导段切换时机的选择，以及交接时制导律的设计.

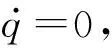
(14)

忽略攻角的影响，则前置角与目标视差角有关，将弹药导引头视场大小设定为[-φ,φ]，那么目标前置角绝对值应小于

(15)

时初制导段与末制导段间进行过渡，以确保导引头不会在视场中丢失目标.

过渡段制导律的加入目的是为了实现制导律切换的平滑过渡，以避免发生初末段制导律在切换时，需用过载剧烈震荡. 文献[15]提出的2阶平滑交接律将过渡段过载设计为初制导段过载与末制导段过载的加权和，

(17)

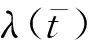
2.4 制导方案

仿生分段复合制导律的制导回路如图4所示. 在制导律工作开始前，需要根据导引头的探测视场大小，弹药的飞行速度和目标运动速度，利用式(15)确定初末段制导交接点，然后制导流程如下：

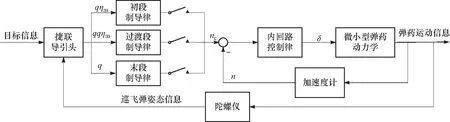
图4 仿生分段复合制导律制导回路Fig.4 Guidance loop of biomimetic subsection compound guidance law

第1步，根据式(9)进行初段制导，让弹药快速地进入尾追目标状态；

第2步，导引头不断获取目标的前置角信息，当其小于初始设置的交接点值时，切换到过渡段制导律；

第3步，设置过渡段时间，并利用过渡段制导律式(16)引导弹药追踪目标；

第4步，当过渡段时间一到，结束过渡段制导，并运用末段制导律式(13)引导弹药直到击中目标.

3 仿真验证

分别在铅垂平面和水平面内运用仿生分段复合制导律来模拟某翼展为1.2 m，重为1.1 kg的微小型弹药攻击地面目标. 仿真条件见表1.

表1 主要结构仿真材料参数Tab 1 Materials properties

在仿真过程中分别采用比例导引[16]和仿生分段制导律得到过载曲线，弹目弹道曲线，攻角侧滑角曲线，目标视场角曲线及姿态角曲线如图5～14所示.

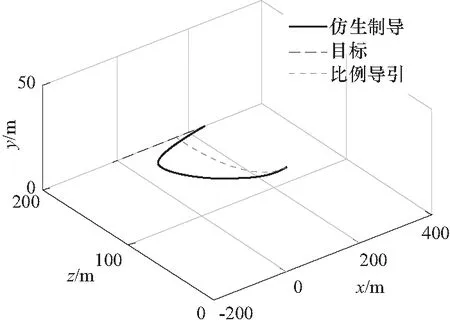
图5 弹目弹道曲线Fig.5 Trajectory curve of loitering munition and target

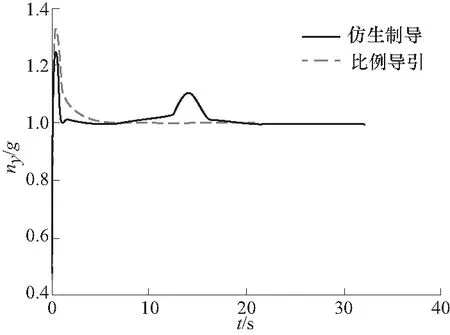
图6 铅垂平面上过载曲线Fig.6 Overload curve on vertical plane

图7 水平面上过载曲线Fig.7 Overload curve on horizontal plane

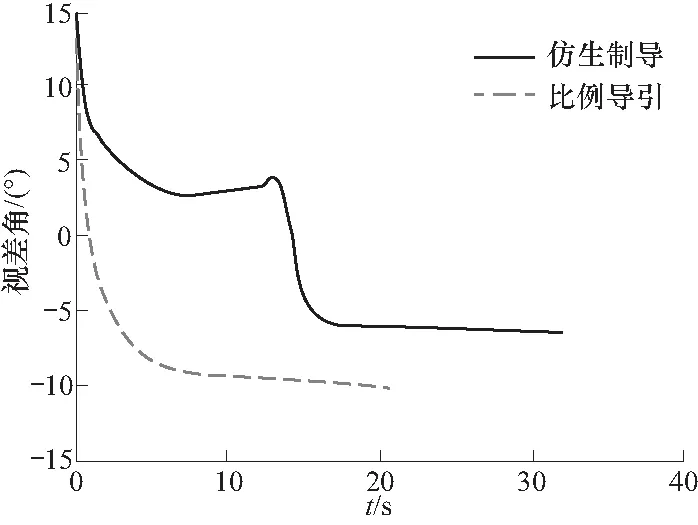
图8 铅垂平面上目标视差角曲线Fig.8 Parallax curve of target on vertical plane

图9 水平面上目标视差角曲线Fig.9 Parallax curve of target on horizontal plane

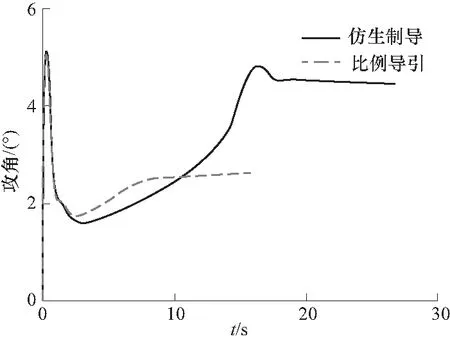
图10 攻角曲线Fig.10 Angle of attack curve

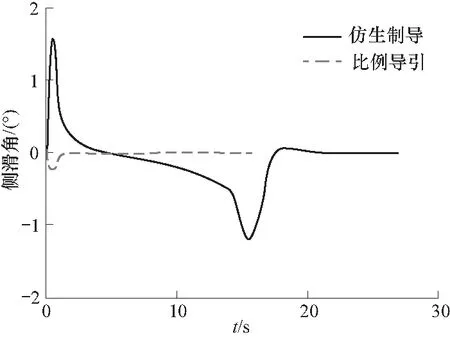
图11 侧滑角曲线Fig.11 Side slip angle curve

图12 俯仰角曲线Fig.12 Pitch angle curve

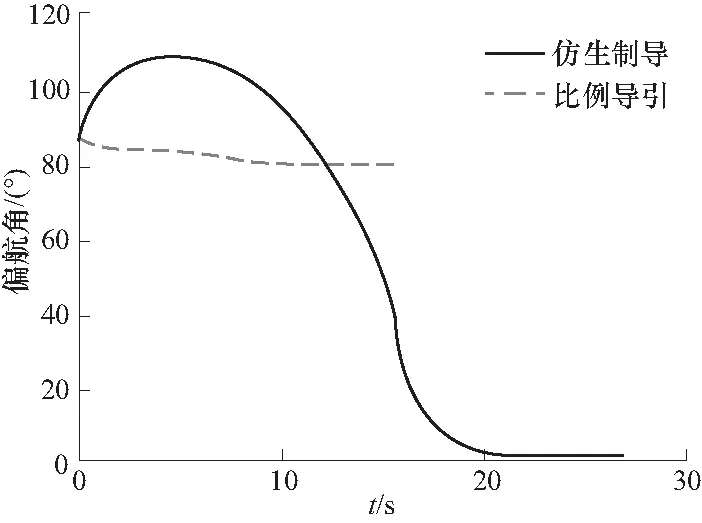
图13 偏航角曲线Fig.13 Yaw angle curve

图14 滚转角曲线Fig.14 Roll angle curve

由仿真结果图分析，当弹目速度比为1.375时，弹药初始状态处于对目标的迎击姿态，设计的复合制导律需要较长的拦截时间，但复合制导律的需用过载更小，并且复合制导过程中的目标视差角始终小于比例导引.

从图9中看到比例导引的最大视差角达到40°以上，已经远远超出导引头的视场范围，结果会使制导末端目标的丢失，本文所设计的分段复合制导的视差角处于(-20°，20°)，完全符合导引头规定的视场角范围.

4 结 论

从蜻蜓的这种捕食策略可以看出，不管它是在搜索目标还是追踪目标的初末段，都是在采用隐蔽性的追踪策略，并将目标始终至于蜻蜓的视场范围内，而蜻蜓在捕捉点的过载也保持在一个较小的值. 蜻蜓的这种追踪策略时千百年进化而来的最优化追踪策略.

针对带有捷联光学导引头的低成本微小型弹药末段追踪目标问题，基于自然界飞行昆虫的抓捕策略设计完成了类似蜻蜓机动策略的分段仿生制导律，末制导初始段利用滑模控制律对视差角进行控制，使弹药姿态调整至尾追目标的状态，在末制导段运用弹道平直特点的运动伪装制导律进行目标攻击.

本文所设计的制导律达到了蜻蜓在捕食果蝇过程中的某些优点，在迎击拦截与弹药速度相近的运动目标时，仿生分段复合制导与比例导引律相比，在末制导段中弹药的需用过载小，目标更接近视场中心位置，能够减小弹药在末制导段受机体的可用过载和导引头的视场限制，有效提高攻击精度.