基于数据驱动的小型柔性翼飞行器控制研究

张之得， 王正杰， 郝智渊

(1.北京理工大学 机电学院，北京 100081；2.中国航空研究院，北京 100012)

单兵便携式飞行器近来发展迅速，其中针对固定翼飞行器发展出了很多种便携的方式：充气机翼的方式、折叠机翼的方式以及可卷曲机翼的方式[1]. 由于单兵便携式小型飞行器具有质量小，飞行速度低的特点，在复杂多变的环境中，对于它的飞行来说，两个固有的问题就是阵风的干扰以及部署任务的空间和时间有限. 随着复合材料以及控制技术的发展，柔性翼无人机被认为是最有潜力解决这些问题的机型[2]. 目前已经进入大众视野的可卷曲机翼飞行器有Prioria公司的MAVERICK，ARA公司的Nighthawk以及以多款佛罗里达大学为典型代表研究的微小型柔性翼飞行器样机.

当前对阵风减缓的研究仍然处于开放活跃的阶段. 已有文献中不乏表明柔性机翼被动变形确实能够有效减缓阵风的影响的研究成果[3-6]. 小型柔性翼的灵感来自于弗罗里达大学的研究人员对飞行动物飞行特性的研究，通过对无人机机翼和飞行动物翅膀之间的比较，提出了适合在低雷诺数条件下飞行的翼型，同时通过对刚体和柔性机翼进行气动分析对比，发现柔性机翼可以有效提高升阻比和气动特性.

目前针对小型柔性翼飞行器，相关研究人员对其的概念内涵、柔性机翼的设计制作、空气动力学评估建模以及飞行试验等内容进行了系统的研究工作，但是关于控制方面的内容还未见相关的文章，由于柔性机翼建模复杂、气动数据难以获得，大量研究工作集中在如何解决刚柔耦合建模问题. 基于数据驱动的控制方法的出现弥补了现代控制理论基于的精确被控对象有时难以建立的缺憾，侯忠生先生曾对数据驱动的控制方法的概念内涵及其包含的方法做了详细的介绍，并对数据驱动的控制方法的存在背景以及适用环境作了阐述[7].

无模型自适应控制(MFAC)方法，作为数据驱动的控制方法中的一种，是侯忠生于1994年在其博士论文中提出的，并由其学生金尚泰、王卫红等[8-9]对其内涵作了详细补充，目前无模型自适应控制方法已经发展为一种较为系统、较为成熟的控制理论，其基本思想是利用一个新引入的伪梯度向量(或伪雅各比矩阵)和伪阶数的概念，在受控系统轨线附近用一系列的动态线性时变模型(紧格式、偏格式、全格式线性化模型)来替代一般离散时间非线性系统，并仅用受控系统的I/O数据来在线估计系统的伪梯度向量，从而实现非线性系统的MFAC. 侯忠生曾发表多篇论述无模型自适应控制的发展状况的文章[10-12]，针对建模复杂，成本较高的情况，阐述了无模型自适应控制方法的优势所在，并提出了几种与基于模型的控制方法优势互补的模块化设计方法，既肯定了现有的基于模型设计的控制方法的优势，也对无模型自适应控制方法未来的发展潜力作出了肯定. 根据近几年的文献调研，可以看出无模型自适应控制方法一直活跃在控制领域，越来越多的研究人员将无模型自适应控制方法应用到城市交通[13-14]、气泡水位控制[15]以及飞行器控制[16-21]等60多个不同领域，并取得了良好的控制效果.

本文将针对一型无副翼飞行器在飞行试验中反映出来的控制问题，基于无模型自适应控制方法设计一种多入多出的无模型自适应控制与前馈式PID控制器串联的控制方案，并通过数值仿真实验验证该控制方案的有效性.

1 数据分析与问题描述

本文研究的小型柔性翼飞行器样机如图1所示， 采用上单翼，十字尾翼，后推式动力的布局，由于柔性机翼要卷曲入筒，没有安装类似副翼的主动变形装置，采用全动平尾的同动，控制飞机俯仰运动；采用全动平尾的差动，控制飞机的滚转运动；采用双垂尾结构，控制飞行器的偏航运动. 全动平尾同动差动联合同时控制俯仰和滚转运动时会产生相对单通道控制更大的舵偏量，当舵面攻角超过其气动线性范围时就将出现严重的非线性气动特性，从而加剧俯仰和滚转通道耦合对自稳控制性能的影响.

图1 小型柔性翼飞行器样机Fig.1 A small flexible wing aircraft prototype

小型柔性翼飞行器参数如表1所示.

表1 飞行器参数Tab.1 Aircraft parameters

小型柔性翼飞行器以手抛方式起飞，由于飞行器为静不稳设计，因此从起飞阶段就以自稳模式进行飞行，为了保证飞行的充分性，在空中巡航阶段，进行多次绕圈飞行，最后阶段将飞行模式从自稳飞行切换到手动模式，观察飞行器飞行状态，由飞手感受飞行器的控制灵敏度. 其中自稳控制器采用串联PID控制器. 具体的飞行过程方案及实际飞行如图2所示.

图2 飞行试验方案示意图Fig.2 Flight test plan

从图3高度曲线的变化规律，可以将实际飞行过程分为6个阶段：① 起飞前测试阶段；② 手抛起飞爬升阶段；③ 不控制俯仰姿态的盘旋阶段；④ 控制俯仰姿态的盘旋阶段；⑤ 切为手动模式飞行阶段；⑥ 坠机之后到断电过程. 其中在阶段④，由于同时控制了俯仰和滚转通道的运动，因此该阶段从理论分析上是耦合最严重的阶段，极易出现控制效果不佳的状态.

图3 高度变化曲线Fig.3 Height curve

下面将从滚转角、滚转角速度、俯仰角、俯仰角速度以及偏航角速度对期望值的跟踪曲线上总结该小型柔性翼飞行器存在的控制问题.

综合各图，通过对比对应阶段④的同时控制俯仰和偏航时刻的自稳控制跟踪效果，如图4，图5，以及图8中，滚转和偏航明显出现跟踪滞后的情况；相比而言，滚转角速度相比俯仰以及偏航角速度的跟踪情况更差.

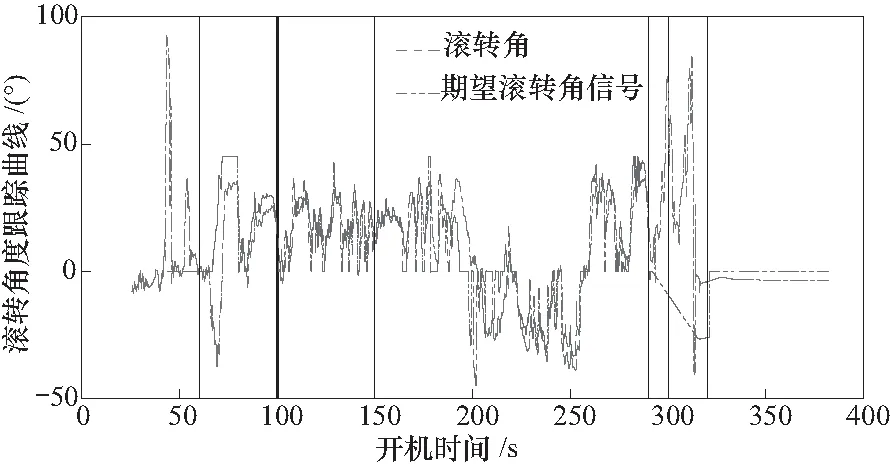
图4 滚转角对期望信号的跟踪曲线Fig.4 Tracking curve of the roll angle to the desired signal

图5 滚转角速度对期望信号的跟踪曲线Fig.5 Tracking curve of the roll angle rate to the desired signal

图6 俯仰角对期望信号的跟踪曲线Fig.6 Tracking curve of the pitch angle to the desired signal

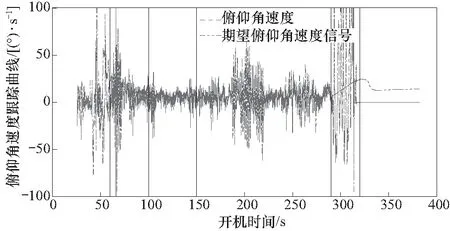
图7 俯仰角速度对期望信号的跟踪曲线Fig.7 Tracking curve of the pitch angle rate to the desired signal

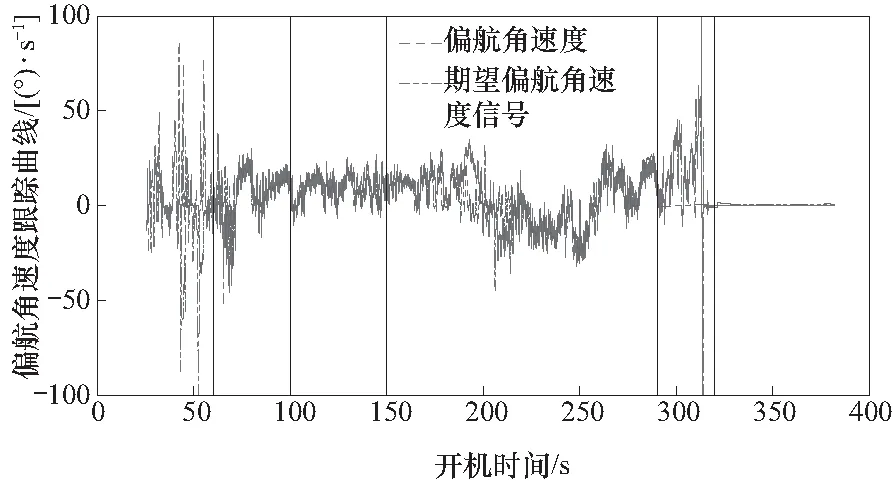
图8 偏航角速度对期望滚转信号的跟踪曲线Fig.8 Tracking curve of the yaw angle rate to the desired signal

通过飞行试验数据分析现得出关于小型柔性翼飞行器以下控制问题：

① 由于控制滚转运动的差动平尾控制面的控制力矩较小，在控制过程中，控制面的气动参数范围很容易进入非线性区域，因此对滚转通道控制器的设计相比于常规的副翼设计的飞行器要复杂一些，尤其是对这个非线性范围不可知的情况；

② 由于本文的小型柔性翼飞行器对滚转和俯仰运动进行控制的机构都为平尾全动舵面，因此相比于常规布局的飞行器，在姿态稳定控制过程中，横纵向的耦合程度更复杂，控制难度更大.

为了解决这两个问题，接下来给出一种基于数据驱动的无模型自适应控制方案.

2 无模型自适应控制方案设计

2.1 紧格式无模型自适应控制算法

无模型自适应控制器根据动态线性化方法的不同可以分为3类：基于紧格式动态线性化的无模型自适应控制(CFDL-MFAC)、基于偏格式动态线性化的无模型自适应控制(PFDL-MFAC)和基于全格式动态线性化的无模型自适应控制(FFDL-MFAC). 其中CFDL-MFAC由于结构最简单，已在近100个各类实际系统中得到应用. 本文也主要基于CFDL-MFAC进行控制器的设计，下文中提到的无模型自适应控制器都特指紧格式无模型自适应控制.

考虑到实验数据分析总结的控制问题，针对小型柔性翼飞行器的横纵向姿态多输入多输出 (MIMO)非线性系统，进行MIMO的无模型自适应控制器的设计.

考虑一类MIMO离散时间非线性系统如下：

y(k+1)=f(y(k),…,y(k-ny),

u(k),…,u(k-nu))

(1)

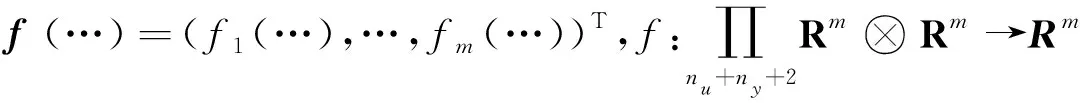
作出如下假设：

假设1 除有限时刻点外，fi(…)，i=1,2,…,m，关于第(ny+2)个变量的偏导数是连续的.

假设2 除有限时刻点外，系统满足广义Lipschitz条件，即对任意k1≠k2,k1,k2≥0和u(k1)≠u(k2)有

‖y(k1+1)-y(k2+1)‖≤b‖u(k1)-u(k2)‖

(2)

其中，y(ki+1)=f(y(ki),…,y(ki-ny),u(ki),…,u(ki-nu))，i=1,2；b>0是一个常数.

当系统满足假设1、2，并且有‖Δu(k)‖≠0时，非线性系统可以用如下动态线性化模型等价表达式,

Δy(k+1)=Φc(k)Δu(k)

(3)

其中，

(4)

为系统的伪雅各比矩阵(PJM).

证明：见文献[8].

考虑如下控制输入准则函数

J(u(k))=‖y*(k+1)-y(k+1)‖2+

λ‖u(k)-u(k-1)‖2

(5)

其中，λ>0是一个权重因子，用来限制控制输入量的变化；y*(k+1)为期望的输出信号，将式(3)代入准则函数(5)中，对u(k)求导，并令其等于0，可得控制算法

(y*(k+1)-y(k))

(6)

其中ρ∈(0,1]为步长因子. 式(6)中的Φc(k)的估计方法如下所述.

考虑如下参数估计准则函数

J(Φc(k))=‖y(k)-y(k-1)-Φc(k)Δu(k-1)‖2+

μ‖Φc(k)-Φc(k-1)‖2

(7)

其中μ>0为权重因子. 对式(7)求极小值，可得PJM的估计算法为

(8)

综合前面所得到的PJM估计算法(8)及控制算法(6)，可给出多入多出离散时间非线性系统的紧格式MAFC控制方案如下，

(9)

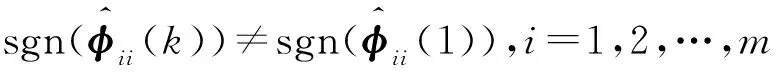
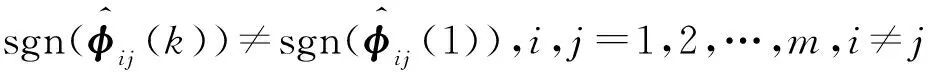
(y*(k+1)-y(k))

(10)

该控制器的设计过程中没有设计到任何的被控对象模型信息，利用的只是系统输入输出数据，故被成为无模型自适应控制，该算法需要调试的参数较少，计算简单，易于工程实现，控制框图如图9所示.

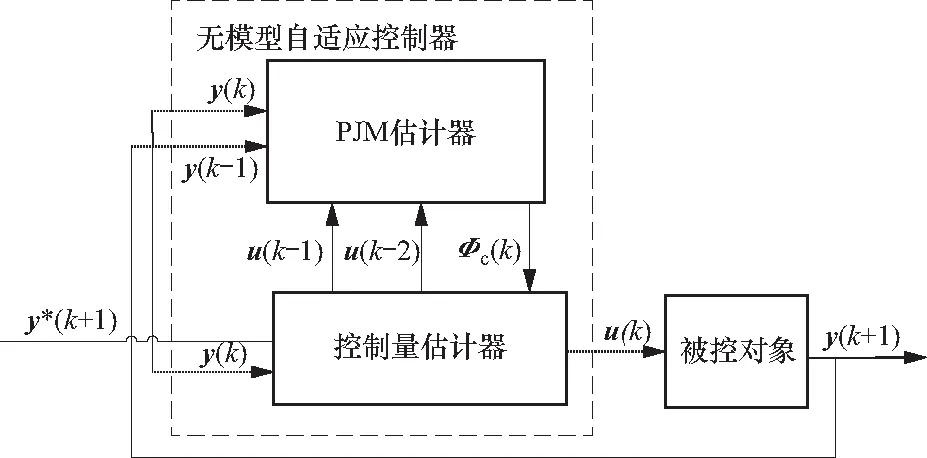
图9 基于MIMO非线性系统的紧格式无模型自适应控制框图Fig.9 Compact format model-free adaptive control block diagram based on MIMO nonlinear system

综上所述，非线性多输入多输出系统的紧格式MFAC设计一般步骤如下：

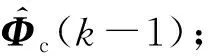
步骤3 利用测量输入输出数据，根据式(10)得出新的控制量u(k)，然后再根据系统(1)得到新的系统输出y(k+1)，进而得出一组新的测量数据.

重复以上步骤，即可使系统的输出值越来越逼近期望值.

2.2 MIMO的MFAC-PI+FF控制方案

通过相关文献对其稳定性的具体分析发现，CFDL-MFAC控制算法不适用于非自衡系统，即开环不稳定的系统. 本文设计的小型柔性翼飞行器在纵向上是静不稳的，因此不能直接利用一般的CFDL-MFAC控制算法，为了解决这类问题，郑健[20]在其论文中提出一种改进的MFAC控制方法，在原控制输入准则函数中加入了对于跟踪误差变化率即1阶差分以及该变化率的改变值即2阶差分项；同时又提出一种MFAC-PID串级控制方案，先使用传统的PID控制方法镇定非自衡系统，再使用紧格式MFAC进行控制，仿真结果表明使用MFAC-PID串级控制方案控制效果更好，鲁棒性更强.

本文在应用无模型自适应控制算法时借鉴该结论，在设计控制器的时候也采用串级控制方案，为解决小型柔性翼飞行器横纵向耦合严重的问题，本小节主要从多输入多输出的角度设计控制器，已知的无论是MIMO线性系统还是MIMO非线性系统的自适应控制，它们都需要精确已知受控系统的数学模型，尤其是输入输出之间准确的耦合关系，而这个耦合关系对于本文的小型柔性翼飞行器很难确定，因此提出MIMO非线性系统的串级紧格式动态线性化无模型自适应和前馈PI控制器(CFDL-MFAC-PI+FF).

具体控制框图如图10所示.

图10 基于MIMO非线性系统的CFDL-MFAC-PI+FF控制框图Fig.10 CFDL-MFAC-PI+FF control block diagram based on MIMO nonlinear system

(11)

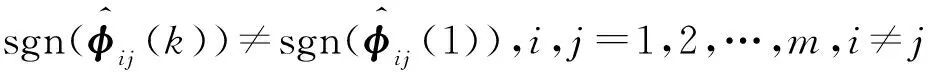
[y*(k+1)-y(k)]

(12)

而内回路中PI+FF控制方式为常规的PID控制器形式，内回路PI+FF控制器构成一个随动控制系统，有效提高了系统的稳定性，同时可以提高系统响应速度；主回路CFDL-MFAC控制器相比于基于模型的控制算法，可以更好地解决模型失配问题，而相比于传统的PID控制器，则可以有效解决非线性问题，增强系统的鲁棒性.

3 仿真验证

为验证上边内容给出的控制方案的有效性，本节将在Simulink环境下，针对前期设计的PID控制器和本章搭建的基于MIMO的MFAC-PI+FF控制器进行仿真实验，通过引入不同模块来模拟仿真模型相比于真实飞行过程中飞行器模型的失配问题，通过仿真实验验证无模型自适应控制方法的控制方案对解决所提出的问题的有效性.

仿真条件见表2.

表2 仿真初始条件Tab.2 Simulation initial condition

本文研究的模型失配问题主要针对第2节提出的两个控制问题，一个是关于控制舵面的力矩气动参数非线性化问题，另一个则是由控制舵作用效果引起的横纵向耦合问题，分别就这两个问题对飞行器模型引入模型失配项.

3.1 控制舵面的力矩气动参数非线性化问题

飞行器控制舵面的偏转会受到舵机及结构机械限幅等的影响，一般控制舵偏限幅在-30°～30°的范围；其实真实飞行过程中，平板翼随着攻角的增大，其提供的升力会随着攻角的增大，逐渐出现非线性变化，为了考察该非线性因素对控制器的影响，在仿真模型中对控制舵面产生的力矩模块中再加入一个非线性限幅模块，意在表述当控制舵面偏转到一定角度之后，将不会产生更大的控制力矩. 此时观察控制器对新模型的适应性.

图11和图12分别表示在加入了非线性限幅模块后，滚转角和俯仰角关于阶跃信号的响应曲线；表3和表4分别表示在加入了非线性限幅模块后，滚转角和俯仰角关于阶跃信号响应的性能指标.

图11 加限幅模块的滚转角阶跃信号响应曲线Fig.11 Roll angle signal response curve with limiter module

图12 加了限幅模块的俯仰角阶跃信号响应曲线Fig.12 Pitch angle signal response curve with limiter module

表3 加限幅模块的滚转角阶跃信号响应的性能指标Tab.3 Performance index of the roll angle step signal response of the limiter module

表4 加限幅模块的俯仰角阶跃信号响应的性能指标Tab.4 Performance index of the pitch angle step signal response of the limiter module

从上图和表中可以看到，在加入了非线性限幅模块后，整体上姿态控制效果相比没加非线性限幅模块要变得更差，但是仍然都能稳定在期望的控制信号附近. 对于滚转姿态的控制，MFAC-PI+FF控制器和P-PI+FF控制器的调节时间都急剧增加，这是因为平尾舵差动控制滚转的能力本身较小，在加入了非线性限幅后，对于滚转机动性有很大的制约；对于俯仰姿态的稳定，可以看到MFAC-PI+FF控制器比P-PI+FF控制器有更快的调节时间，更小的超调量，这些都可以看出基于 MIMO设计的MFAC-PI+FF控制器相比于基于SISO设计的P-PI+FF控制器有更好的鲁棒性.

3.2 平尾控制舵作用效果引起的横纵向耦合问题

为了分析由同一平尾控制面控制滚转和俯仰运动带来的耦合问题，本文通过将滚转控制量引起的力矩乘以一个比例因子引入到俯仰通道力矩计算模块中，将俯仰控制量引起的力矩乘以一个比例因子引入到滚转通道力矩计算模块中，来模拟控制舵面偏转对横纵向运动的耦合作用. 此时观察控制器对新模型的控制效果.

图13和图14分别表示在增加了平尾舵偏引起的横纵向耦合模块后，滚转角和俯仰角关于阶跃信号的响应曲线.

图13 加平尾舵偏引起的横纵向耦合的滚转角阶跃信号响应曲线Fig.13 Roll angle step response curve of transverse and longitudinal coupling caused by flat tail rudder

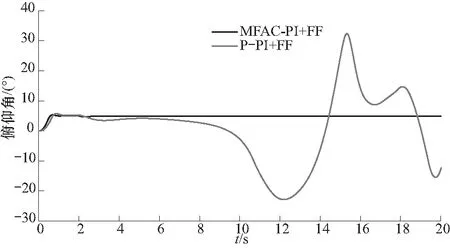
图14 加平尾舵偏引起的横纵向耦合的俯仰角阶跃信号响应曲线Fig.14 Pitch angle step response curve of transverse and longitudinal coupling caused by flat tail rudder

从图13和图14中可以看出，当增加平尾控制舵的舵偏对滚转和俯仰的耦合影响时，该影响因子取一个较大值时，传统的基于SISO设计的P-PI+FF控制器对于俯仰和滚转姿态的稳定出现发散现象，而基于MIMO设计的MFAC-PI+FF控制器在俯仰通道上仍能稳定在期望俯仰角附近，而对于滚转角的稳定，虽然能稳定在一个滚转角上，但是此时相比于期望的滚转角信号具有较大的稳态误差.

综上所述，基于MIMO设计的MFAC-PI+FF控制器相比基于SISO设计的P-PI+FF控制器具有更好的鲁棒性.

4 结 论

本文针对已通过飞行试验验证过的小型柔性翼飞行器平台，根据试验得到的姿态传感器数据对传统PID姿态控制器的性能进行了分析并得出该飞行器使用传统PID控制器难以克服的两个问题.

提出一种无模型自适应控制方法，利用紧格式动态线性法对飞行器动力学非线性模型进行等效，进而设计了紧格式无模型自适应控制算法与PID控制算法串联的MFAC-PI+FF控制方案.

通过仿真试验，验证了该算法在解决通过飞行试验数据提出的两个飞行控制问题上的有效性.