通风竖井地压计算

江俊杰 方志峰 刘永鹏 李小勇 陈代华 廖杭

为了科学地指导竖井设计施工、降低竖井施工风险，往往会对竖井地压进行估算。文章依托白马隧道通风竖井工程，首先通过弹性理论获得了竖井周边围岩的应力分布规律，同时基于莫尔圆极限平衡状态算出了井壁不会出现非线性变形的稳定条件，由此计算得出竖井的稳定深度为5.27 m，最后通过对竖井变形地压的计算进行了竖井支护参数对比，研究发现当初支混凝土采用厚度为32 cm、强度等级为C35时，支护效益最好。研究成果对类似工程具有一定参考价值。

公路隧道; 通风竖井; 变形地压; 支护参数对比

U455.8   A

[定稿日期]2021-07-22

[作者简介]江俊杰 （1983～），男，本科，高级工程师，主要从事隧道施工管理工作。

目前竖井作为一种大型通风道广泛应用于长大隧道的建设中[1-3]。竖井除了通风作用，还可以增加主洞开挖工作面，故而许多长大隧道为了缩短工期，常常在靠近隧道中部位置修建竖井[4]。随着竖井建设需求的增大，复杂地质条件下的深大竖井逐渐出现，有些工程前期地质勘察不够、对地压估计不足，出现了一系列事故。研究竖井地压对于竖井科学的设计施工、安全运营有着深远意义。

国内外许多学者对于竖井地压展开了大量研究。谢永利等[5]采用模型试验分析了竖井地压的变化规律，以此讨论了减少竖井地压的方法;王勍等[6]采用了数值模拟对竖井进行了安全性评价，并结合现场竖井周边应力、应变监测等多种方法管理地压，保证了竖井的安全;谢永利等[7]通过着手分析竖井周围的滑移线场并得到滑移线方程，由此展开竖井地压变化规律的研究;马英明[8]介绍了集中竖井地压的计算方法并对这些计算方法做出了评价。

本文依托白马隧道通风竖井工程，通过弹性理论获得了竖井周边围岩应力分布规律，同时基于莫尔圆极限平衡状态获得了井壁的稳定条件并由此计算得出了竖井的稳定深度，最后通过对竖井变形地压的计算和不同工况下支护参数的对比确定了竖井最合理的支护参数。研究成果对类似工程具有一定参考价值。

1 工程概况

白马隧道出口端（绵阳端）位于四川省平武县白马藏族乡亚者造祖村，穿白马至九寨沟县勿角乡蒲南村。隧道左线起讫桩号为K34+707～K47+720，长13 013 m;右线隧道起论桩号为YK34+664～K47+664，长13 000 m，最大埋深约1 092 m，属深埋特长隧道。

隧道中部设置两通风竖井，井身段穿过的主要岩性为板岩，岩性较软，层间结合较差，同时风化较严重，围岩等级为Ⅴ级，竖井纵剖面如图1所示。

2 极限深度计算

2.1 竖井周边稳定条件

竖井围岩中的软弱夹层是造成井壁变形破坏的主要因素，竖井设计中应对有代表性的软弱夹层进行稳定性验算。在竖井地质勘测过程中发现大量板岩夹砂和砂岩夹板岩的情况，可将其视为含软弱夹层地压计算。

在竖井周边取一小块单元体来研究，如图2所示。其上作用的应力可表示为：

σz=γH

σθ=2γHμ/（1-μ）

σr=0（1）

式中：σz为铅垂应力，单位为MPa;σθ为切向应力，单位为MPa;σr为径向应力，单位为MPa;γ为岩体重度，单位为kN/m3;μ为岩体泊松比;H为该点埋深，单位为m。

在判定出σz与σθ哪个是最大主应力σmax后，用σmax绘制莫尔圆，看其是否与强度曲线相切。如果莫尔圆在岩体强度曲线以下，说明衍生的剪应力τ<σtanφ+C，因而，井壁是稳定的;如果与强度曲线相切，则说明井壁岩体处于极限平衡状态。

由图2（b）可知，当井壁岩体处于极限平衡状态时，根据摩尔圆与强度曲线相切的关系，有：

sinφ=σmax/2σmax/2+Ccotφ（2）

（1-sinφ）σmax/2=Ccotφsinφ=Ccosφ（3）

联立式（2）和式（3），得到：

σmax=2Ccosφ1-sinφ（4）

从而可知井壁的稳定条件为：

σmax≤2Ccosφ1-sinφ（5）

式（5）也可转换为：

σmax≤2Ccosφ1-sinφ=2Csin（φ+90）1+cos（φ+90）=2Ctan（φ+90）2（6）

2.2 竖井围岩应力分布

在自然条件下，未开挖竖井的岩体中已存在相互平衡的原岩应力，在竖井开挖后，对岩体的扰动破坏了岩体的应力状态，进而引起竖井周围岩体朝着新的平衡状态进行应力重新分布（图3）。

若把竖井看作一个半无限体的垂直孔，垂直竖井轴线截取以薄片来研究，如图3所示。由于岩体自重应力在水平方向引起的水平应力为q=γH/（1-μ），设岩体为各向同性的弹性体，则可把它视为一个圆孔的双向等压板。根据弹性力学分析可知，离豎井中心r处的径向应力σr和切向应力σθ 分别为：

σr=μ1-μγH（1-a2r2）

σθ=μ1-μγH（1+a2r2）（7）

式中：μ为竖井围岩的泊松比;γ为围岩的重度，单位kN/m3;H为研究断面以上覆盖岩层的厚度，单位m;a为竖井断面半径，单位m;r研究点距离竖井中心的距离，单位m。

由式7知，在竖井周边上，即r=a时，有：

σr=0σθ=2μ1-μγH（8）

由式8知，竖井周边上的径向应力σr=0，切向应力σθ为原岩水平应力的2倍。随着r的不同，其应力分布为如图4（b）所示的状态。尽管在竖井周边的水平面上有较大的应力集中，但铅垂方向的应力σz仍有可能是竖井周边上的最大主应力σmax，至于最大主应力σmax到底出现在水平方向还是铅垂方向由围岩的泊松比μ的大小决定。

由式（1）可得，要使：

σθ=2γHμ/（1-μ）≥σz=γH（9）

有：

μ>1/3（10）

即当μ>1/3时，有σmax=σθ=2γHμ/（1-μ）;当即μ<1/3时，σmax=σz=γH。

2.3 竖井稳定深度计算

按竖井周边稳定条件计算极限深度H0，如图4所示。如果计算压力处H1< H0，则说明井壁应力集中不会使该软弱岩层产生非弹性变形，井壁能够承受上覆岩层的压力而不破坏;若计算处深度H2>H0，则说明竖井开挖后井壁应力集中使该岩层内出现非弹性变化区，甚至引起井身失稳，必须对井壁进行压力计算。

由井壁稳定条件公式6可知，软弱夹层在该深度的最大主应力有如下两种情况：

当σmax=σz=γH0时，有：

γH0≤2Ctanφ+902（11）

H0≤2Cγtanφ+902（12）

当σmax=σθ=2γH0μ/（1-μ）时，有：

2γH0μ/（1-μ）≤2Ctanφ+902（13）

H0≤Cγμtanφ+902（1-μ）（14）

在深度小于H0的上覆岩层作用下，竖井井壁并不会出现非弹性变形，处于稳定状态，H0即是竖井的稳定深度。

竖井井身所处围岩环境其力学参数如表1所示。

由式（10）、式（14）可得，竖井稳定深度为：

H0≤Cγμtanφ+902（1-μ）=5.27m

上述计算了未进行支护条件下竖井井壁的破坏深度，在5.27 m以上深度覆盖岩层作用下，井壁不会出现非弹性变形，不会破坏;在5.27 m以下的位置，井壁在围岩应力作用下发生非弹性变形而破坏。

3 竖井变形地压计算

当非弹性变形区内发生塑性流动时，会出现变形地压，将衬砌视为厚壁圆筒，根据弹性理论，衬砌上压力和变形关系式为：

pa=μbEb[1-rarb2]/2ra（15）

式中：pa为衬砌外侧表面所受的压力，单位为kPa;μb为衬砌外侧表面的径向变形;ra、rb为衬砌内、外半径，单位为m;Eb为衬砌弹性模量，单位为MPa。

根据围岩与支护相互作用原理，利用支护反力与竖井围岩位移关系式，可计算圆形竖井周边位移，即：

μa=rbsinφ（rb+Ccotφ）2G[（1-sinφ）（p0+Ccotφ）pi+Ccotφ]1-sinφsinφ（16）

G=E/2（1+μ）（17）

式中：μa为围岩径向位移，，单位为m ;pi为支护强度，单位为kPa;rb为衬砌外半径，单位为m，可近似取竖井断面半径，即rb=a;p0为原岩应力，单位為kPa;C为围岩内聚力，单位为kPa;φ为围岩内摩擦角;G为剪切弹性模量，单位为MPa，可通过式（17）计算得。

因为μa=μb，且pi=pa，联立式（15）、式（16）可解得衬砌外侧表面所受的压力pa。

4 支护参数选取

4.1 初支混凝土型号选择

在竖井地质勘测过程中发现大量板岩夹砂和砂岩夹板岩的情况，可将其视为含软弱夹层地压计算，可根据式（15）、式（16）得到衬砌在不同深度下，外侧所受压力与衬砌变形量大小。

针对不同型号的混凝土，见表2。当初支厚度为22 cm时，竖井深度与衬砌外侧压力pa、变形量μb之间的关系如图5所示。

图5为在不同混凝土强度下井深与衬砌外侧压力、变形量之间的关系图。由图5（a）～图5（d）知，衬砌外侧压力pa随着井深呈线性增加，各混凝土强度下衬砌外侧压力pa差距不大。由图5（e）可知，竖井变形量μb也随着井深呈线性增加。当竖井深度在0～100 m内时，各混凝土强度下衬砌位移量相差不大，基本位移量均在0～20 mm;当深度超过100 m时，4种不同强度等级混凝土对衬砌位移量影响渐渐体现，随着混凝土强度提高，竖井位移量逐渐降低，但降低速度逐渐减缓，如C30较C25对衬砌位移量影响较明显，但C35较C30对衬砌位移量的影响明显度下降，C35、C40强度的混凝土其位移量直线基本重合，说明在相同的衬砌厚度下C35、C40对位移控制量基本相同，此时将C35衬砌改为C40，提高混凝土强度进一步控制衬砌位移量意义不大。

综上，建议采用的初支混凝土强度为C30、C35。当初衬的厚度为22 cm时，井深超过100 m后，初衬位移量超过了20 mm;在井底时，初衬变形量高达70 mm，所以衬砌厚度22 cm无法满足现场支护要求，需加厚初衬。

4.2 初支混凝土厚度选择

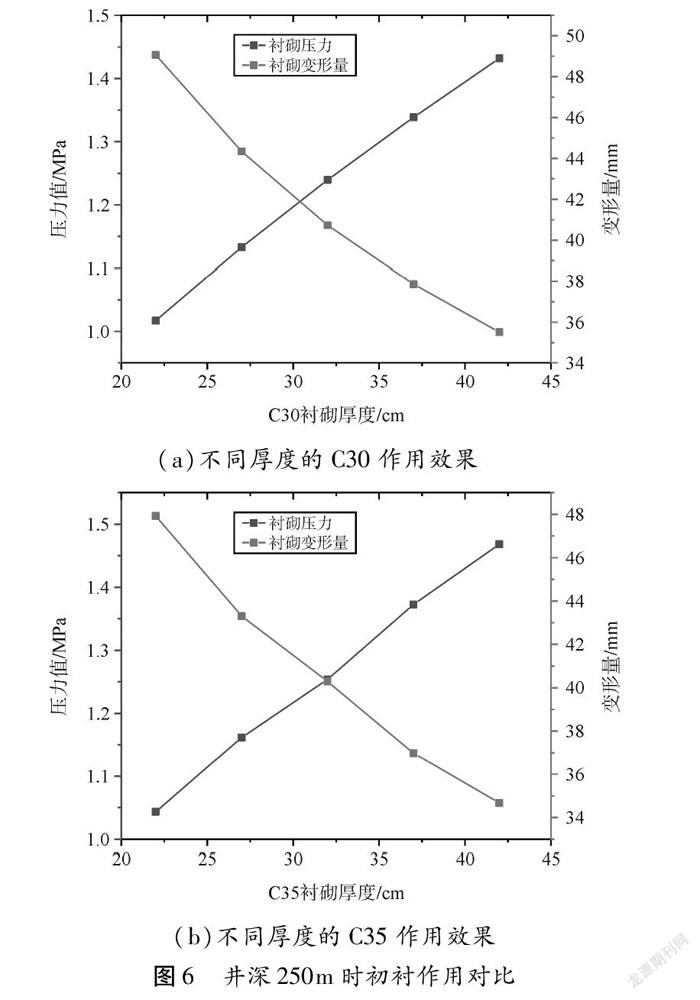
通过4.1节的计算可知，最合适的混凝土强度等级为C30或C35，同时衬砌混凝土厚度为22 cm无法满足现场支护安全要求，因此将C30或C35混凝土衬砌在不同厚度下比较其变形量及衬砌压力情况（表3），从而选择合理的衬砌厚度，选取井深分别为250 m、350 m处进行分析。

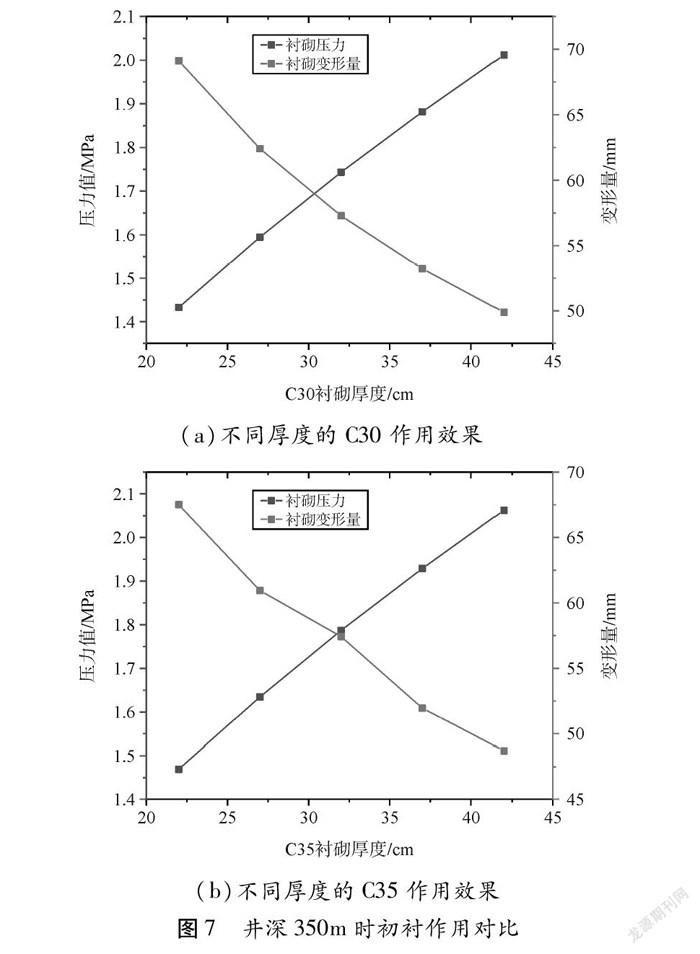
根据支护与围岩变形相协调支护原理，图6、图7反映了支护特性曲线与围岩特性曲线二者之间共同作用关系，随着衬砌厚度增加，支护强度近线性进一步提高，衬砌位移量同样呈近线性递减，图中二者之间的交点所对应的厚度属于该型号衬砌最为合理的支护厚度，即一方面围岩在衬砌作用下，产生一定的位移，应力得到一定程度释放;同时，衬砌也不会因为所受应力太高而造成压坏的情况。

从图6、图7中可以看出C30的最合理支护厚度为31 cm，C35的最合理支护厚度为32 cm，同时在不同深度处，C35最合理厚度对应的初支变形量相对于型号为C30的小，进而初支混凝土可选取厚度为32 cm的C35。通过对比图5～图7可看出，相比提高衬砌支护强度，提高衬砌厚度能够更加有效地控制围岩位移量。

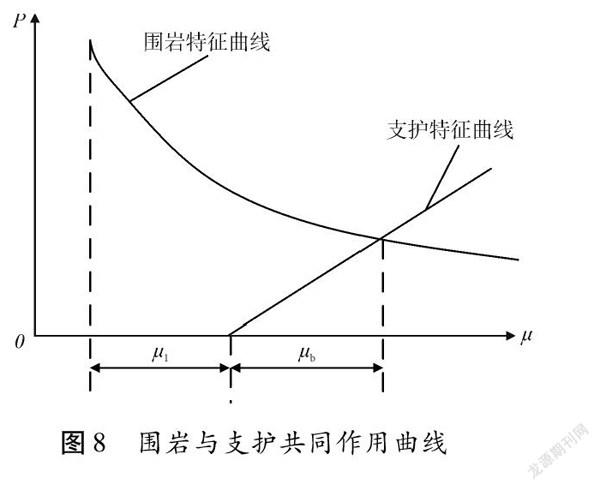
让压型支护理论认为，软岩工程围岩变形大。让压应避开初期来压，为围岩变形留一个空间，在压力得到一定能够程度释放以后，再进行支护，在支护前围岩已经产生一定的位移，如图8所示。支护刚度和强度变小，使得支护受力减小，周边径向位移增加。根据这一原理，在施工过程中有柔性支护与刚性支护的区别，允许井壁有一定的变形，从而减小后期围岩变形时给初衬所带来的压力，减小支护的受力。岩体性质越软，围岩特性曲线越向外外移，变形也就越大;支护时间越迟，支护曲线起点离坐标原点越远，支护工作压力也就越低。

考虑竖井为V级围岩，围岩中存在大量风化的板岩，因此在后期围岩可能存在长期的蠕变变形，因此在考虑竖井支护方案中初衬选择强度较弱的支护方案，为竖井围岩后期提供一定的预留变形量，另一方面提高二衬的支护强度从而保证最后的支护强度能够满足竖井的安全要求。

5 结束语

基于弹性理论以及围岩与支护相互作用原理对白马隧道通风竖井进行地压计算，得到了如下结论：

（1）深度为5.27 m以上时，竖井井壁在围岩应力作用下只会发生弹性变形，处于稳定状态;在深度为5.27 m以下，竖井井壁在围岩应力作用下将发生非弹性变形而破坏。

（2）根据地压计算结果，竖井衬砌外侧压力和衬砌外侧变形与井深基本成线性递增规律，增大衬砌厚度或者衬砌强度都可以减小衬砌外侧变形量。通过参数对比发现初衬采用厚度为32 cm强度等级为C35的混凝土时支护效益最好。

（3）根据让压型支护理论，为了减少初支的压力，竖井开挖后应避开初期来压，先释放部分围岩压力后再进行支护。

参考文献

[1] 王文，孙三祥.隧道竖井外流场模拟及风塔外型结构优化研究[J].中国安全生产科学技术，2020，16（6）：140-146.

[2] 王永东，覃桢杰，何志伟，等.公路隧道互补结合竖井送排的改進型混合通风方式研究[J].中国公路学报， 2020，33（4）：106-114.

[3] 王文，孙三祥，何世洋.隧道救援站通风网络优化设计及人员疏散研究[J].中国安全生产科学技术， 2020， 16 （8）： 57-62.

[4] 曾大仁，李胜宗，黄淮彬.雪山隧道从竖井增辟工作面施工探讨[J].隧道建设，2007（S2）：337-343.

[5] 谢永利，顾安全.关于竖井散体地压的研究[J].长安大学学报：自然科学版，1989（1）：82-92..

[6] 王勍，王洪江.浅议竖井保安矿柱回收的地压控制问题[J].有色金属（矿山部分），2004（4）：21-24.

[7] 谢永利，郭建生.滑移线场理论在竖井散体地压分析中的应用[J].西安公路交通大学学报，1994（1）：6-13.

[8] 马英明.深表土竖井地压的计算方法[J].煤炭科学技术，1979（1）：16-22.

3590500589221