基于模糊贝叶斯网络的管幕箱涵顶进安全评估



下穿既有道路超浅埋顶管施工中易对环境产生不利的影响,且影响因素多,缺乏精确数据统计资料,传统风险评估方法难以处理。文章提出了一种基于模糊贝叶斯网络的风险评估方法,采用模糊数描述各类风险事件风险状态及风险发生概率,利用专家评分方法,获取了各类风险事件发生可能性,通过模糊贝叶斯网络正向推理算出各节点不同风险状态下风险发生概率。并以南昌赣江大道南昌大桥西桥头路段非机动车道改造工程为依托,验证了此方法的有效性。实例结果表明,此方法能有效的评估施工中的风险事件风险等级,可以成为工程安全风险管理中的工具。
地下工程; 管幕法; 箱涵顶进; 模糊贝叶斯网络; 安全风险评估
U449.82 A
[定稿日期]2021-05-17
[作者简介]左志鹏(1991~),男,硕士,工程师,主要从事市政桥梁设计工作。
管幕箱涵顶进工法是利用小口径顶管机建造大断面地下空间的新型施工技术。采用该方法施工时,先利用顶管设备将小口径钢管逐根顶入土体,钢管间依靠锁口相连,在管幕的保护下利用顶进设备边开挖边顶进预制箱涵,完成建设的一种方法[1]。由于该方法工效高,对地层适应性较强,在近年的城市建设中得到较多应用。采用该方法施工超浅埋下穿既有道路的隧道时,由于顶进断面大,覆土浅,适用地层条件较差,周边环境对沉降敏感性较高等原因,施工易对环境产生不利的影响。众多学者对管幕箱涵顶进施工技术和施工引发的变形问题开展了大量研究[2-4],但关于施工中的风险识别及评估的研究较少[5]。且其施工过程中影响因素多,缺乏精确的数据统计资料,传统的风险评估方法难以处理。本文提出了一种基于模糊贝叶斯网络的管幕预制箱涵顶进施工风险评估方法,利用模糊数描述事件发生状态和发生概率的模糊性,并利用专家评分法获取风险事件发生概率,通过模糊贝叶斯网络确定本工程整体、各类风险事件的风险状态及其发生的风险概率。该方法可以为相关工程建设过程中的风险识别和风险评估提供参考。
1 模糊贝叶斯网络模型
1.1 贝叶斯网络方法
贝叶斯网络是一种结合了概率论和图论概率模型。包含两个部分:网络图形结构及网络参数。网络图形结构包括网络节点和连接节点的有向弧,节点表示变量,有向边表示变量间依赖关系。每一个节点都有一个条件概率表(CPT),用来表示该节点与其父节点的相关关系。网络参数主要指贝叶斯网络的条件概率表集合。贝叶斯网络中子节点与除父节点外的节点条件独立,如式(1)所示。
Pxiπ(xi),A(xi)=Pxiπ(xi)(1)
式中:π(xi)为节点xi的父节点集合,A(xi)为节点xi父节点之外的其他节点集合。
利用n个变量联合概率分布式及节点间条件独立性可以得出贝叶斯网络联合概率分布。式(2)为贝叶斯网络联合概率分布式:
P(x1,x2,…,xn)=P(x1)P(x2x1)…P(xnx1,x2,…,xn-1)
=∏ni=1P(xix1,x2,…,xn-1)=∏ni=1P[xiπ(xi)(2)
其中,当π(xi)为空集时,P(xi|π(xi))即为边缘分布P(xi)。
1.2 模糊贝叶斯網络节点描述
1.2.1 节点故障状态描述
传统贝叶斯网络认为节点只有故障和非故障两种状态,然而在实际情况下,节点状态可能存在介于“故障”与“正常”的中间态,存在模糊性。仅用二态描述节点状态是不准确的。本文认为节点有3种故障状态:完全故障、中等故障、无故障。在节点CPT中分别用0、1、2表示。
1.2.2 节点故障概率描述
节点故障率的确定通常需要精确的统计资料,然而实际中的数据资料往往难以满足统计需要。因此本文采用模糊数描述节点故障率。模糊数形式有很多种,包括:梯形模糊数、正态模糊数、三角模糊数、LR模糊数等。其中三角模糊数形式简洁明了,运算方便,得到了广泛的应用[6]为计算方便,本文采用三角模糊数作为节点故障率描述函数。三角模糊数通常可以记为F=(a, b, c)。其隶属函数如式3所示,隶属函数如图1所示。
μF=xm-l-lm-lx∈[l,m]
xm-u-um-ux∈[m,u]
0其他(3)
式中:l≤m≤u,l为最小可能值;u为最大可能取值;m为最可能值。
2 管幕箱涵顶进安全风险评估流程
2.1 管幕箱涵顶进安全风险贝叶斯网络构建
在模糊贝叶斯网络构建时可以选择由故障树转化构造的方式进行。故障树能全面系统的描述故障可能发生的原因,能直观反映出基本事件间逻辑关系。可以在顶进施工安全风险故障树的基础上,通过故障树向贝叶斯网络转换规则,将深基坑施工安全风险故障树转换为深基坑施工安全风险贝叶斯网络[7]。这样可以充分利用故障树在风险识别,风险因素相互逻辑关系定义方面的优势。
转换时,故障树中底事件、中间事件、顶事件分别与模糊贝叶斯网络中的根节点、中间节点、叶节点对应。故障树中存在多个事件时,转换后只建立一个节点;故障树中逻辑门通过调整条件概率表CPT的数值关系反映。
2.2 根节点先验概率的获取
2.2.1 专家意见的获取
获取根节点先验概率时,有两种不同的方式。在有大量统计样本资料时,可以根据统计资料获取节点先验概率;在没有统计资料情况下通常采用专家评分法获取先验概率。具体做法为:引入非常低、低、偏低、中等、偏高、高、非常高7个概率语言描述变量。并邀请具有不同经验背景、教育背景具备丰富地下工程设计、施工经验的专家若干名,合自己的经验,给出每个节点不同状态下的语言发生概率。再将语言概率转换为模糊概率。语言变量对应的模糊数见表1和图2。
2.2.2 专家意见的合成
考虑到不同教育背景、相关专业从业年限对判断的准确性有影响,在综合专家意见时,按照不同学历、不同从业年限对专家意见进行加权。不同学历和不同从业年限加权表如表2所示,最终按式(4)综合专家意见。
ij=∑nk=1αkβkkij∑nk=1αkβk(4)
式中:αk代表第k个专家的学历权重;βk代表第k个专家从业年限的权重;kij代表第k个专家针对第i个节点的;第j种状态提出的语言概率描述值所转化的模糊数;ij代表第i个节点第j种状态最终综合专家意见后的意见。
2.2.3 解模糊
专家评判意见是模糊概率,模糊概率经过模糊贝叶斯网络概率推理后其结果仍然是模糊概率。后续风险等级的确定及便于对比同节点不同状态发生概率,必须对模糊概率进行去模糊处理。去模糊是指从模糊集合中选取一个最能代表这个模糊集合的单值的过程。去模糊的方法有很多种,包括均值面积法、重心法、积分值法、加权平均法、隶属度限幅元素平均法[8]等。由于均值面积法具有概念清晰计算方便等特点,本文采用均值面积法进行去模糊处理[9]。
若節点Y处于状态Yq下的三角模糊概率值为(T=Tq)=(a,m,b),则经过式(3)换算后的精确概率P(Tq)′如式(5)所示。
P(Tq)′=a+2m+b4(5)
2.2.4 归一处理
经过解模糊处理后,同一节点各状态下概率和不一定为1,为满足这一要求,需要用式(6)对根结点发生概率进行归一化处理。
Pij=P′ij∑ri-1j=1p′ij(6)
其中:Pij是归一化之后的i节点j状态的发生概率;P′ij是归一化之前的i节点j状态的发生概率。
2.3 事故发生概率预测
在构建了模糊贝叶斯网络之后,可以利用模糊贝叶斯网络正向推理,通过已知节点的概率推理出其他节点概率。已知根节点各种故障状态的故障率为P(Xaii),根据贝叶斯网络概率推理算法[10]可以由桶消元法[11]求得叶节点T任意故障状态Ta的模糊概率如式(7)所示。
T=Ta=∑X1,X2,…Xn,B1.B2,…BnP~(X1,X2,…Xn,B1,B2,…
Bm,T=Ta)=∑λ(T)[T=Taλ(T)]×
∑λ(y1)[y1λ(y1)]×∑λ(y2)[y2λ(y2)]×…
×∑λ(ym)[ymλ(ym)]×(Xa11)×P~(Xa22)×…×(Xann)(7)
式中,λ(T)和λ(yi)分别为叶节点及中间节点的父节点集合;P(Xaii)为根节点xi故障状态为xaii的故障率。
3 工程应用
3.1 工程概况
依托工程为南昌赣江大道南昌大桥西桥头路段非机动车道改造工程,车道标准断面宽7 m,双向通行。采用管幕箱涵下穿既有南昌大桥西桥头路基路段,通道采用分离式双箱双孔断面,分上下两幅通行,单孔通道净宽5 m,净高3.3 m。顶管暗埋段部分全长24 m,顶管暗埋段两侧穿越地层为路基,主要为回填砂,无地下水。由于道路标高和净高限制,暗埋段埋深仅约1.5 m,在顶管通道四周设置管幕形成超前支护帷幕。管幕长度为25 m,两侧洞门结构各宽0.5 m,工程位置如图3所示,箱涵与既有路基关系如图4所示。
3.2 风险识别
文献[12]及文献[13]系统地分析了管幕顶管施工过程中存在的风险,并对各种风险的发生频率进行了评估。参照其研究成果,结合本工程实际情况,可以建立本工程施工中的故障树。并可以按照故障树向贝叶斯网络转换规则,构建本工程模糊贝叶斯网络。如图5所示,事件如表3所示。
3.3 风险评估
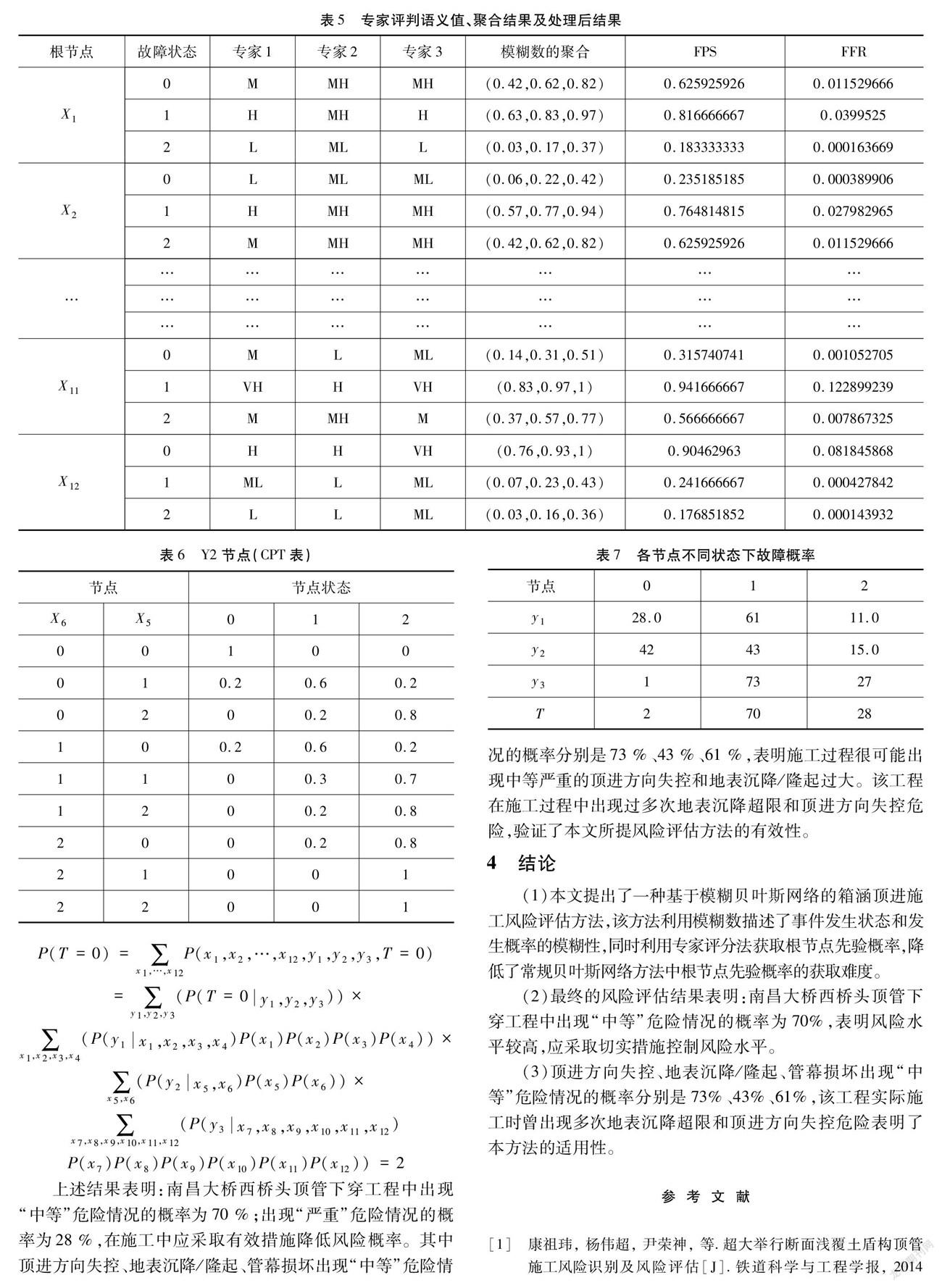
为获取根节点先验概率,本文邀请3位分别从属于高校、设计单位、施工单位专家分别依据自己的经验结合工程项目实际情况给出节点不同故障状态下的故障率情况,3位专家权重如表4所示。并按照3.2节所述方法经过去模糊处理后得到各根节点在不同故障状态下的故障概率,如表5所示。
节点CPT是根据事件间相互逻辑关系由专家结合工程实际状况给出。限于篇幅仅列出Y2节点CPT如表6所示。根据表6中各节点不同状态下故障概率及节点条件概率表CPT,可以求得叶节点T各故障状态的发生概率。同样的方法可以算出各节点在不同状态下的故障概率,如表7所示。
上述结果表明:南昌大桥西桥头顶管下穿工程中出现“中等”危险情况的概率为70 %;出现“严重”危险情况的概率为28 %,在施工中应采取有效措施降低风险概率。其中顶进方向失控、地表沉降/隆起、管幕损坏出现“中等”危险情况的概率分别是73 %、43 %、61 %,表明施工过程很可能出现中等严重的顶进方向失控和地表沉降/隆起过大。该工程在施工过程中出现过多次地表沉降超限和顶进方向失控危险,验证了本文所提风险评估方法的有效性。
4 结论
(1)本文提出了一种基于模糊贝叶斯网络的箱涵顶进施工风险评估方法,该方法利用模糊数描述了事件发生状态和发生概率的模糊性,同时利用专家评分法获取根节点先验概率,降低了常规贝叶斯网络方法中根节点先验概率的获取难度。
(2)最终的风险评估结果表明:南昌大桥西桥头顶管下穿工程中出现“中等”危险情况的概率为70%,表明风险水平较高,应采取切实措施控制风险水平。
(3)顶进方向失控、地表沉降/隆起、管幕损坏出现“中等”危险情况的概率分别是73%、43%、61%,该工程实际施工时曾出现多次地表沉降超限和顶进方向失控危险表明了本方法的适用性。
参考文献
[1] 康祖玮, 杨伟超, 尹荣神, 等.超大举行断面浅覆土盾构顶管施工风险识别及风险评估[J].铁道科学与工程学报, 2014(5): 1105-1112.
[2] 王剑, 邓宗伟. 某超大直径断面顶管施工引起的地层位移分析[J].铁道科学与工程学报, 2014, 11(2): 95-100.
[3] 贾连辉. 超大断面矩形盾构顶管设计关键技术[J]. 隧道建设, 2014, 34(11): 1098-1106.
[4] 房营光, 莫海鸿, 张传英. 顶管施工扰动区土体变形的理论与实测分析[J]. 岩石力学与工程学报, 2003, 22(4): 601-605.
[5] 彭立敏, 王哲, 叶艺超, 等. 矩形顶管技术发展与研究现状[J]. 隧道建设, 2015, 35(1): 1098-1106.
[6] ZHAO L J, WANG X L, QIAN Y.Analysis of Factors that Influence Hazardous Material Transportation Accidents Based on Bayesian Networks:A Case Study in China [J].Safety Science, 2012, 50(4): 1049-1055.
[7] BOBBIO A, PORTINALE L,MINICHINO M, et al. Improving the Analysis of Dependable Systems by Mapping Fault Trees into Bayesian Networks[J]. Reliability Engineering & System Safety, 2001, 71(3):249-260.
[8] 陆莹, 李启明, 周志鹏.基于模糊贝叶斯网络的地铁运营安全风险预测[J].东南大学学报:自然科学版, 2010, 40(5): 1110-1114.
[9] 兰蓉, 范九伦. 三角模糊数上的完备度量及其在决策中的应用[J]. 系统工程学报, 2010, 25(3):313-319.
[10] WEBER P, JOUFFE L. Complex system reliability modeling with dynamic object oriented bayesian networks(DOOBN)[J]. Reliability Engineering & System safety, 2007, 92(10):1413-1420.
[11] GALLARDO JE T. A representation of human reliability using fuzzy concepts[J]. Information Sciences. 1988,45(2):153-173.
[12] 朱合華, 闫治国, 李向阳, 等.饱和软土地层中管幕法隧道施工风险分析[J].岩石力学与工程学报, 2005(S2): 5549-5554.
[13] 程敏, 曹义敏. 基于模糊FMEA的长距离输水管线顶管施工风险分析[J]. 中国安全科学学报, 2013, 23(9):76-82.
2201501186333

