基于增强烟花算法的移动式储能削峰填谷优化调度

王育飞，郑云平，薛 花，米 阳

（上海电力大学电气工程学院,上海市200090）

0 引言

随着分布式电源的大量接入,配电网面临着负荷峰谷差进一步加大的风险［1-2］。移动式储能系统（mobile energy storage system,MESS）是为应对自然灾害和紧急情况而开发的一种以卡车为载体的后备式储能电源［3-4］。MESS除应急供电外,其闲置情况下可向配电网提供多种服务,如削峰填谷、无功支撑、平滑可再生能源出力等。

采用传统固定式储能系统解决配电网峰谷差过大问题的主要方式有集中式储能和分布式储能［5-6］。然而,固定式储能系统的容量和接入位置一旦确定便不宜更改,其较高的投资成本与运维成本一直是限制其大规模应用的主要因素［7］。与固定式储能不同,MESS兼具可移动性和储能系统特性,可根据负荷曲线特征灵活选取接入位置和合适的容量,能够避免冗余容量造成浪费,减小日常运行维护费用,有效提升削峰填谷的经济性。因此,根据配电系统实际运行情况制定合理的调度策略,对于改善负荷特性,提高发电设备的利用效率具有重要意义［8］。

目前,对于配电系统中不同运行模式下的MESS调度策略研究已取得了一定的成果,但很少专门涉及MESS用于削峰填谷调度策略的研究。文献［9］提出一种适用于MESS的日前能量管理系统,以调压和运行成本最小为目标,根据日前负荷预测建立交通延迟模型,并采用粒子群算法求解得到MESS接入的位置及容量。文献［10］主要考虑MESS的紧急电源作用,以运行成本最小为目标建立双层规划模型,针对不同应用场景确定MESS的最优路线及容量。文献［11］提出了一种用于配电系统中多种服务的MESS调度优化算法,旨在通过考虑MESS参与电网多服务（包括能源套利、电压调节和有功损耗最小化）来最大化配电公司的利润。文献［12］提出一种两阶段调度优化模型,第1阶段考虑配电网正常运行情况下MESS的低储高发套利,第2阶段考虑应急情况下MESS用于提升配电网的弹性。文献［13］提出通过MESS在最佳时间和位置提供充放电服务实现削峰填谷,但并未考虑MESS的容量选择。

移动式储能用于削峰填谷的调度是一个多维非线性问题,采用传统智能算法（如粒子群算法、遗传算法和模拟退火算法）求解此类问题易陷入局部最优［14］。烟花算法（firework algorithm,FWA）［15］采用的是一种分布式信息共享机制,同时基于免疫浓度思想的选择策略来避免早熟。自烟花算法提出以来,已在路径规划［16］、大数据处理［17］、故障诊断［18］等多个领域得到了应用,但目前未见其在移动式储能调度领域中的应用。

基于MESS有功调节灵活性和时空灵活性,论文提出在MESS削峰填谷调度优化中综合考虑MESS削峰填谷的可靠性与经济性。基于分层优化思想,上层综合考虑MESS削峰填谷效果和日净收益,求解各时刻MESS最优充放电功率,确定削峰与填谷时段；下层考虑接入点对网损的影响,确定MESS的最优接入位置和容量。基于烟花算法的特性与优势,提出一种柯西与高斯混合变异的改进增强烟花算法（enhanced firework algorithm,EFWA）求解下层模型。以IEEE 33节点配电网为例,对MESS削峰填谷优化调度结果进行分析。

1 移动式储能削峰填谷双层优化调度模型

MESS用于配电网削峰填谷,在调度时应充分考虑经济性,选择适当容量的MESS在合适的时间段充分发挥削峰或填谷作用,避免冗余容量造成浪费。同时应满足配电网的要求,选择最佳接入位置减少网络损耗并保证各节点电压不发生越限。以一天为一个调度周期,分别确定MESS用于削峰和填谷的最优调度策略。针对MESS削峰填谷调度优化问题,选取的目标函数为削峰填谷效果最优、净收益最大和网损最小。考虑到MESS调度策略的确定计及时序运行状态,将求解过程分为2层进行,其调度结构如图1所示。

上层优化模型中,同时考虑MESS削峰填谷的可靠性与经济性,以削峰填谷效果最优和净收益最大为优化目标；决策变量为一天内MESS的各时刻充放电功率；约束条件包括MESS的功率与荷电状态约束、配电网功率平衡约束；采用混沌粒子群优化（chaos particle swarm optimization,CPSO）算 法求解。

下层模型中,优化目标为MESS接入配电网后网损最小；决策变量为接入各节点的MESS各时刻充放电功率和MESS的接入位置；约束条件包括各时刻MESS总有功出力约束、节点电压约束、支路有功功率约束；采用嵌入潮流计算的改进EFWA求解。

上下层模型间参数传递关系为:上层优化模型求解得到MESS各时刻总充放电功率、削峰与填谷时段和各时段MESS总容量需求,作为参数传递给下层模型,并作为下层优化模型决策变量的约束条件；下层模型分别对削峰时段和填谷时段接入各节点的MESS各时刻出力和MESS接入位置进行寻优,并根据优化结果进行潮流计算,将得到的网损反馈至上层优化模型的功率平衡约束条件中。

图1 MESS削峰填谷双层优化调度结构Fig.1 Structure of bi-level optimal dispatch for peak load shifting with MESS

1.1 上层优化模型

上层优化模型以日前净负荷功率预测曲线为研究对象,目标函数为削峰填谷效果最优和净收益最大,求解MESS各个时刻的总有功出力,并对削峰与填谷时段与各时段总容量需求进行划分。

1.1.1 上层优化模型目标函数

1）削峰填谷效果

电力负荷需求存在不确定性,若某一段时间负荷需求较低,MESS可接入配电网储存一部分能量；若某一段时间负荷需求较高,MESS可接入配电网释放一部分能量。采用等效负荷标准差表征MESS削峰填谷的效果,如式（1）所示。

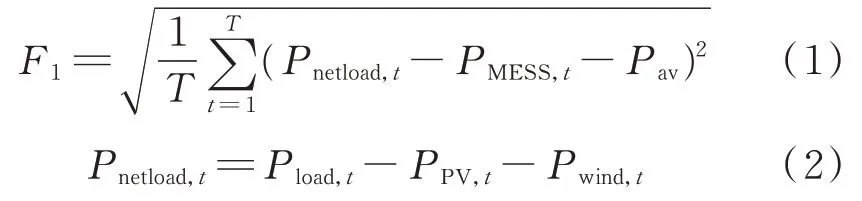
式中:Pnetload,t为t时刻配电网净负荷功率；PMESS,t为t时刻MESS的充放电功率,PMESS,t＞0表示MESS在t时刻向电网释放能量,PMESS,t＜0表示MESS在t时刻向电网吸收能量,PMESS,t=0表示MESS在t时刻既不吸收也不释放能量；T为一天24 h；Pav为净负荷功率平均值；Pload,t、PPV,t、Pwind,t分别为t时刻配电网负荷功率、光伏发电功率和风机发电功率。

2）削峰填谷净收益

配电网中已配置的MESS不仅用于削峰填谷场景,且单次接受调度的MESS只在某个时段进行出力。因此,为准确刻画削峰填谷效益,建立MESS度电成本模型,只计算MESS用于削峰填谷部分的使用成本与收益。单位移动式储能度电成本CLCOE的计算公式［19］为:

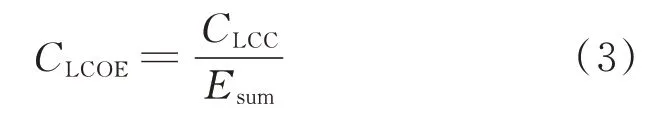
式中:CLCC为MESS全生命周期成本；Esum为MESS寿命期内预期总体转移能量。

其中,MESS全生命周期成本主要包括一次性固定投资成本、运行维护成本和回收残值,如式（4）所示。

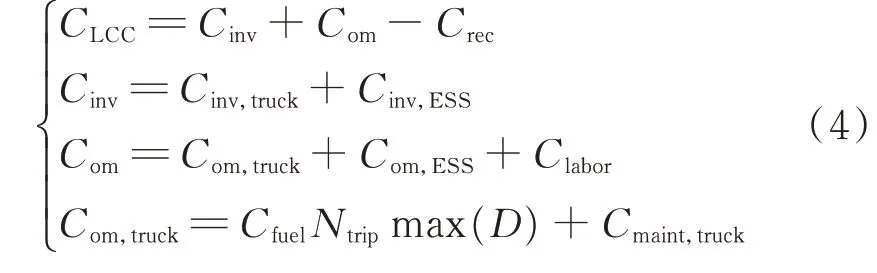
式中:Cinv为MESS一次性固定投资成本,包括卡车投资成本Cinv,truck和储能系统（ESS）一次性投资成本Cinv,ESS；Com为MESS运维成本,包括卡车运维成本Com,truck、ESS运维成本Com,ESS和人工成本Clabor；Crec为MESS回收残值,其值与MESS一次性固定投资成本Cinv相关；Cfuel为卡车的燃料成本；Ntrip为MESS全生命周期内总行程次数；D为MESS单次调度行驶距离,为简便计算,距离取为MESS停放点至最远接入点之间的距离max（D）；Cmaint,truck为卡车维护成本。

MESS在谷时电价时段储存能量,若在峰时电价时段释放能量,峰谷电价差即为利润；若在平时电价释放能量,平谷电价差即为利润。因此,一个调度周期T内MESS削峰填谷的净收益可以表示为:

其中

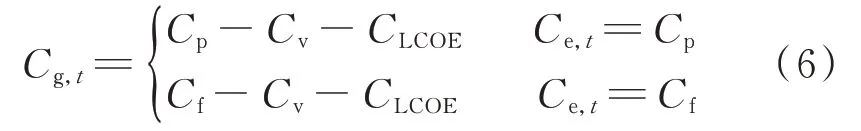
式中:μ为表征MESS在t时刻是否进行放电的标量,若是则μ=1,反之则μ=0；Cg,t为t时刻MESS提供单位电量服务的净收益；Cp、Cv、Cf分别为峰时段电价、谷时段电价和平时段电价；Ce,t为t时刻电价。

上层总目标函数为:

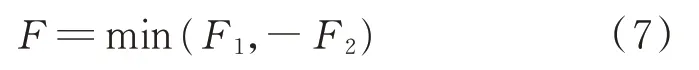
1.1.2 上层优化模型约束条件

1）MESS有功出力约束

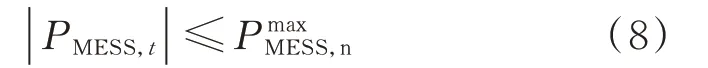
式中:PmaxMESS,n为处于闲置状态的MESS最大总额定功率。

2）MESS荷电状态约束

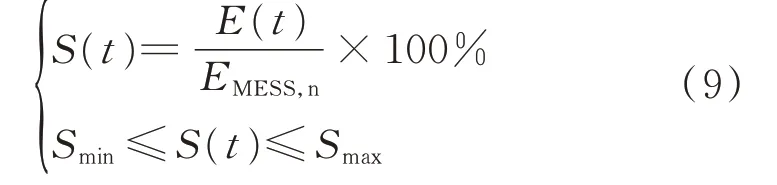
式 中:E（t）为t时 刻MESS的 总 电 量；EMESS,n为MESS的额定电能容量；Smax和Smin分别为MESS荷电状态上、下限值。

3）功率平衡约束

MESS接入配电网后,t时刻MESS充放电功率、发电机组出力、用户负荷应实现功率平衡,即

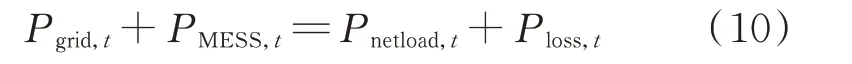
式中:Pgrid,t为t时刻网供功率；Ploss,t为t时刻配电网线路的有功功率损耗。

1.2 下层优化模型

在上层削峰与填谷时段MESS总容量需求确定的前提下,MESS接入位置的不同会对整个配电系统的网损造成影响。因此,下层以配电系统总网损最小为优化目标,对MESS的接入位置进行合理调度。

1.2.1 下层优化模型目标函数

下层优化的目标函数为MESS接入配电系统后削峰或填谷时段内总网损最小,其数学表达式为:

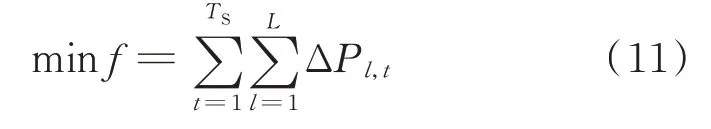
式中:L为配电网总支路数；ΔPl,t为支路l在t时刻的有功线损；TS为削峰或填谷时长。

1.2.2 下层优化模型约束条件

1）各时刻MESS总有功出力约束

各节点接入的MESS在各时刻的总有功出力受到上层决策变量（各时刻MESS充放电功率）的约束,即

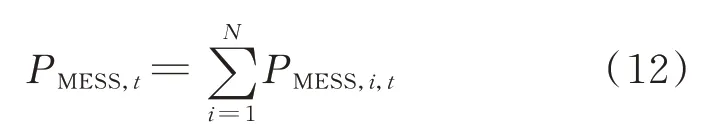
式中:PMESS,i,t为t时刻配电网节点i接入的MESS有功出力；N为配电网节点数。

2）节点电压约束

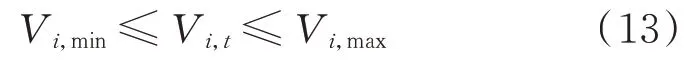
式中:Vi,t为t时刻配电系统节点i的电压；Vi,max和Vi,min分别为节点i电压的上、下限值。

3）支路有功功率约束

为防止线路发生阻塞,t时刻各支路有功潮流应满足所允许传输的有功功率限制,即

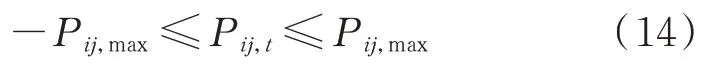
式中:Pij,t为t时刻支路i j传输的有功功率；Pij,max为支路i j传输的有功功率上限。

2 MESS削峰填谷优化调度求解算法

2.1 求解上层模型的CPSO算法

由于上层优化变量维数较高、非线性,采用具有参数设置少、搜索速度快的粒子群算法［20］比较合适。为了加快粒子群体的进化速度,采用基于混沌寻优思想的CPSO算法［21］。

1）目标函数归一化处理。上层各子目标之间存在量纲不一致问题,为了简便模型求解,首先采用归一化方法和设置权重将MESS上层多目标函数转化为单目标函数。

负荷方差属性值为成本型,取值越小越好,而净收益属性值为效益型,取值越大越好。为了使2个目标函数同时参与运算,对F1与F2归一化处理如式（15）所示。

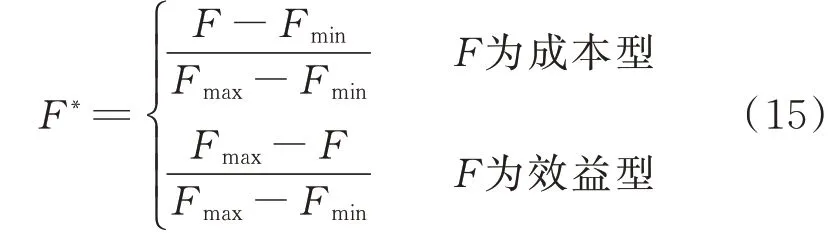
式中:F为目标函数；Fmin和Fmax分别为目标函数F的最小值和最大值。

归一化后得到新的目标函数为:

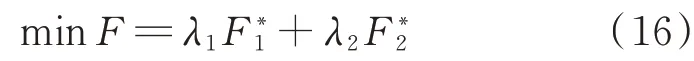
2）粒子编码。

式中:Pm为第m个粒子的位置；Pm,t为第m个粒子在t时刻的坐标,表示MESS在t时刻的充电或放电功率。

3）削峰与填谷时段划分。根据各时刻MESS出力可确定MESS持续充电时段和MESS持续放电时段,各时段开始时间即为MESS应到达时间ta,各时段结束时间即为MESS应离开的时间td。

计算得到MESS各时段的出力值,分别以充电和放电功率中的最大值作为MESS选择额定功率参考数据,充电功率之和以及放电功率之和作为MESS选择额定容量参考数据,最终接受调度的MESS总功率和容量应不小于参考数据。

2.2 求解下层模型的改进EFWA

2.2.1 改进型混合变异EFWA

烟花算法是受到夜空中烟花爆炸的启发而提出的一种群体智能算法。EFWA［22］针对基本烟花算法的性能缺陷提出了最小爆炸半径检测策略和新型高斯变异算子,同时提出一种精英-随机选择策略,有效提升了算法收敛效率和抗干扰能力,降低对初值的敏感性。但是,单一的变异算子依然不能兼顾全局搜索能力和局部搜索能力。因此,在EFWA中引入混合变异算子,以加快算法的收敛速度并提高算法的搜索精度。

对于求解调度问题,要求算法前期应具有较高的全局搜索能力,中后期应具有较高的局部搜索能力。高斯变异算子具有较好的局部搜索能力,柯西变异算子具有较好的全局搜索能力。因此,引入柯西与高斯混合变异算子。柯西分布的概率密度函数为:

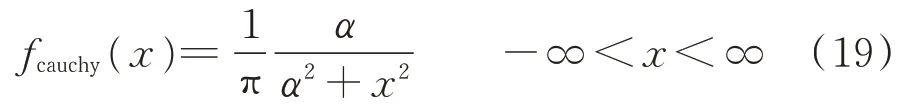
取α=1,标准柯西分布与标准高斯分布曲线见附录A图A1,在原点处柯西分布曲线的峰值较小,烟花爆炸产生变异火花后用于搜索相邻区间的时间相对较少。同时,柯西分布两翼宽于高斯分布且相对平缓,产生的变异步长较大,能够使用更多的时间搜索全局最优值,有利于引导个体跳出局部搜索,提高算法的全局搜索能力。

进行快速全局搜索,迅速定位全局最优解所在的范围,在后期以局部开采能力为主,找到最优解的精确位置。为实现不同求解阶段2种变异算子的切换,引入动态切换概率p∈[0,1],计算公式如下:

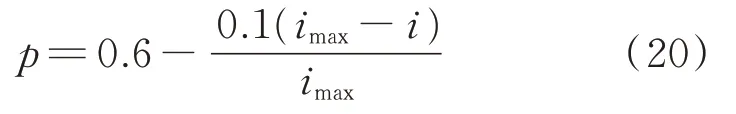
式中:imax和i分别为最大迭代次数和当前迭代次数。

生成随机数r∈[0,1],若p≤r,则采用柯西变异进行全局寻求；若p＞r,则采用高斯变异进行局部寻优。

2.2.2 改进EFWA烟花编码

烟花编码见附录A图A2,每个烟花包括两部分:t时刻接入到各节点MESS的功率和MESS的接入位置。

其中,接入各节点MESS的功率满足式（12）,MESS接入位置满足如下约束:

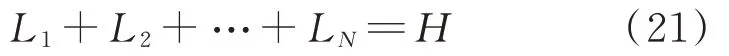
式中:Li的取值为0或1,Li=0表示节点i处不安装MESS,Li=1表示节点i处安装MESS；H为配电网允许MESS最大安装节点个数。

采用改进EFWA求解下层模型的具体步骤如下。

步骤1:确定MESS最大安装节点个数H,当前MESS接入节点个数h=1,MESS接入位置采用二进制改进EFWA进行优化。

步骤2:初始化烟花可行域（各节点允许接入MESS的充放电功率范围）,并从中随机产生M个烟花（接入各节点的MESS各时刻充放电功率）。

步骤3:计算每一个烟花的适应度值（下层目标函数值）,判断是否收敛或达到最大迭代次数。若满足,则h=h+1,否则执行步骤4。

步骤4:计算子代爆炸火花的数量与爆炸幅度,随机选择一定数量的烟花进行变异,对于越界一定范围内的火花映射到可行域内,从中选择部分火花作为子代烟花,并计算目标子代烟花的适应度值。

步骤5:算法结束,对比不同安装节点数下MESS的系统网损,输出最优调度方案。

改进混合变异EFWA求解下层模型详细流程见附录A图A3。

3 算例分析

3.1 算例数据

选取IEEE 33节点配电系统作为算例进行仿真分析,系统结构如图2所示。节点14和21接有装机容量为500 k W的光伏发电单元,节点24和31接有装机容量为500 k W的风力发电单元。网络额定电压UN为12.66 kV,最大负荷为3.715 MW,节点电压上、下限分别取为1.05 UN和0.95 UN。

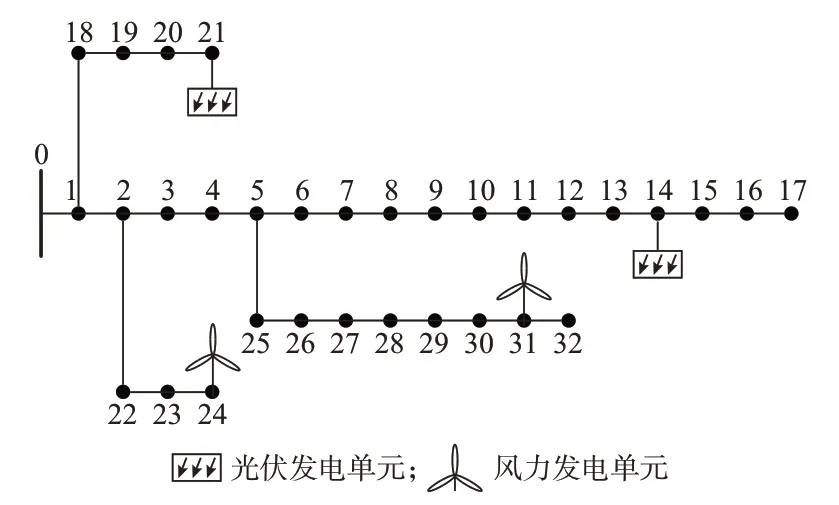
图2 IEEE 33节点配电系统结构Fig.2 Structure of IEEE 33-bus distribution system

假设配电网中已有5种不同容量的MESS可供调度,其参数如表1所示。节点0为平衡节点,因MESS在夜间谷时电价时段需集中充电,为简便潮流计算,将待调度MESS在节点0处统一停放管理。储能采用磷酸铁锂电池,MESS可安装节点为节点2至33,各节点最大允许安装功率为500 k W。为充分利用MESS,本文考虑MESS的荷电状态下限值为0,上限值为1。

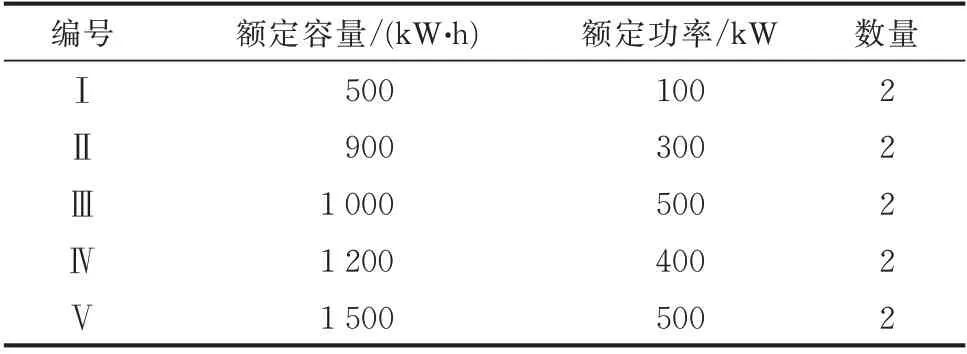
表1 MESS参数Table 1 Parameters of MESS

采用某地区典型日负荷、光伏和风电功率数据作为日前预测数据,合成后的净负荷功率曲线见附录B图B1。可以看出,在下个调度周期内,最大净负荷功率为3 459 kW,最小净负荷功率为579 k W,日平均净负荷功率为1 765 k W,峰谷差为2 880 kW。分时电价见附录B表B1。

3.2 仿真结果分析

3.2.1 算法性能对比

选取CPSO算法、EFWA与改进EFWA进行性能对比。设置权重λ1=0.5和λ2=0.5,MESS接入节点个数为2时,3种算法求解调度结果如表2和表3所示。3种算法各重复运行10次,分别对比削峰与填谷下的最优调度结果。从表2平均适应度值和适应度值均方差可以看出,在算法求解稳定性方面,CPSO算法每次求解所得适应度值波动较大,EFWA稳定性优于CPSO算法,改进EFWA在稳定性方面进一步提升。从表3可以看出,3种算法所求得MESS接入节点均不相同,因此所产生的损耗也不相同,EFWA所得调度结果优于CPSO算法,改进EFWA调度结果优于EFWA和CPSO算法。

表2 3种算法适应度值比较Table 2 Comparison of fitness values of three algorithms

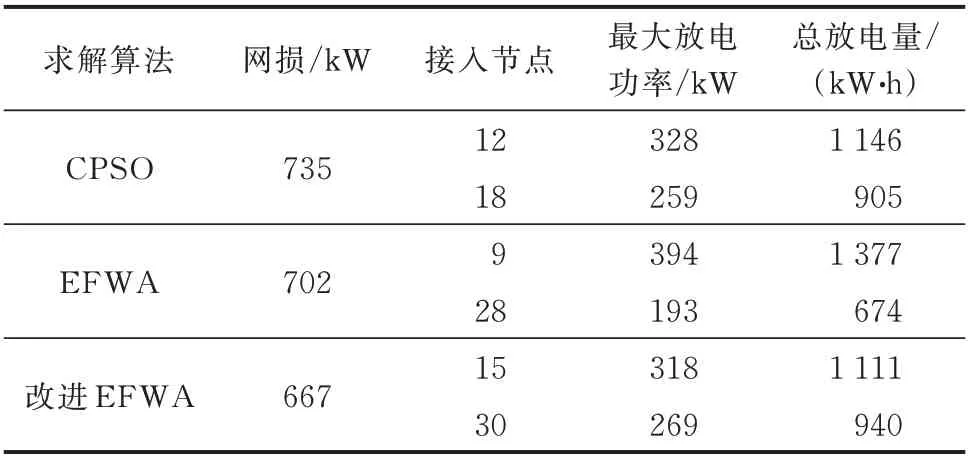
表3 3种算法的削峰求解结果Table 3 Peak shaving results of three algorithms

图3为3种算法求解下层模型的优化性能对比结果。由图可见,对于下层多维MESS选点问题,改进EFWA很好地避免了CPSO算法和EFWA易陷入局部最优的问题,能够更快搜索到全局最优解,具有更快的收敛速度。CPSO算法、EFWA和改进EFWA求解所得最小网损分别为735、702、667 kW,说明相较CPSO算法和EFWA,改进后的EFWA具有更优的求解精度。

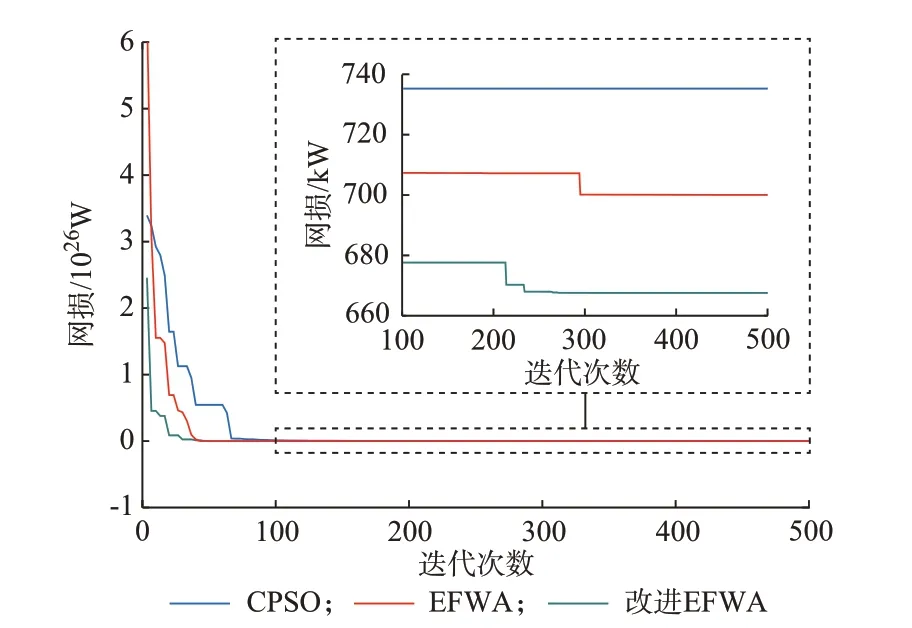
图3 3种算法的优化性能对比Fig.3 Optimization performance comparison of three algorithms

3.2.2 调度结果分析

上层目标函数需先归一化为单目标函数,因此首先利用CPSO算法求得上层各子目标函数的最值见附录B表B2。

归一化后的单目标函数为:

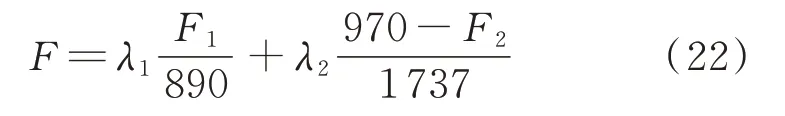
考虑到MESS的其他用途及人工成本,一条馈线内不可能接入过多的MESS,因此设定算例中MESS最大接入节点个数为3,不同节点个数的MESS调度方案如表4所示。

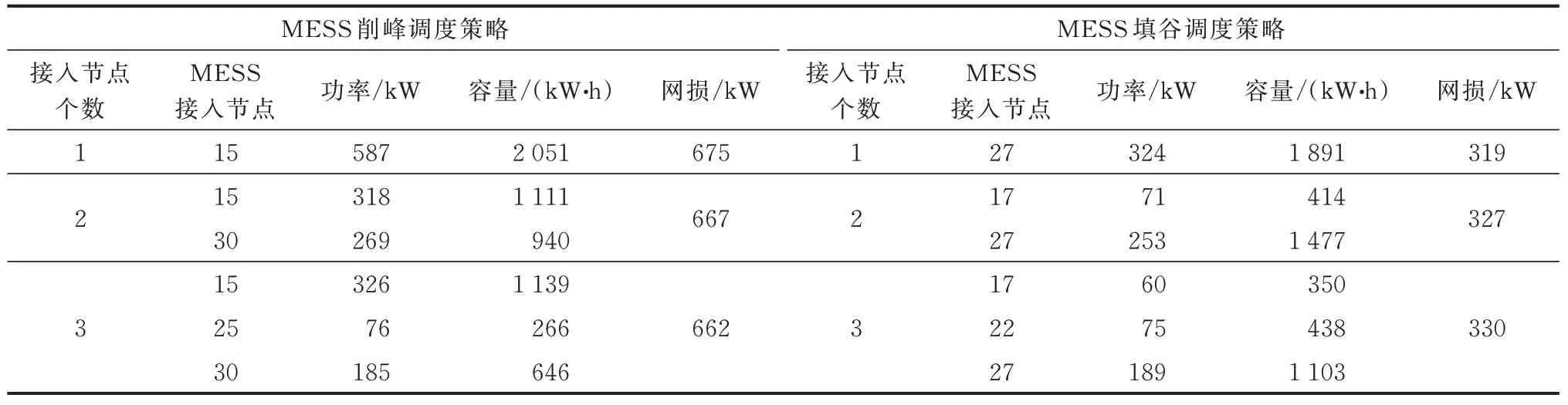
表4 不同接入节点数量下MESS接入方案对比Table 4 C omparison of MESS access schemes with different numbers of access nodes

分析表4可知,当接入节点数为1时,所需MESS额定功率与容量较大,没有与之相匹配的MESS可供选择,且接入节点处电压易发生越限。接入节点个数为2时,已经合理地减小了网络损耗且保证各节点电压处于合格水平。接入节点个数为3时,增加了人工成本且效果与接入节点为2时相差不大。采用所提调度方法得到削峰时段MESS的最优总放电量为2.051 MW∙h,填谷时段MESS的最优总充电量为1.891 MW∙h。

根据所得削峰与填谷时段MESS的最优充放电量和最佳接入节点个数,确定调度方案如附录B表B3所示。2台额定容量分别为100 kW/500 k W∙h和500 k W/1 500 k W∙h的MESS应提前从节点0出发,在00:00之前分别接入节点17和27,00:00至10:00提供充电服务,在10:00之后离开并返回节点0处。2台额定容量分别为400 k W/1 200 k W∙h和500 k W/1 000 k W∙h的MESS应提前从节点0出发,在15:00之前分别接入节点15和30,17:00—23:00提供放电服务,在23:00之后离开并返回节点0处。MESS各时段的SOC变化曲线见附录B图B2。

图4为MESS接入配电网后不同时间各节点电压曲线。从图4可以看出,经过对MESS调度策略进行优化,MESS接入配电网进行削峰填谷,各节点全时段均处于0.95（标幺值）至1.05（标幺值）之间,没有出现电压越限情况。

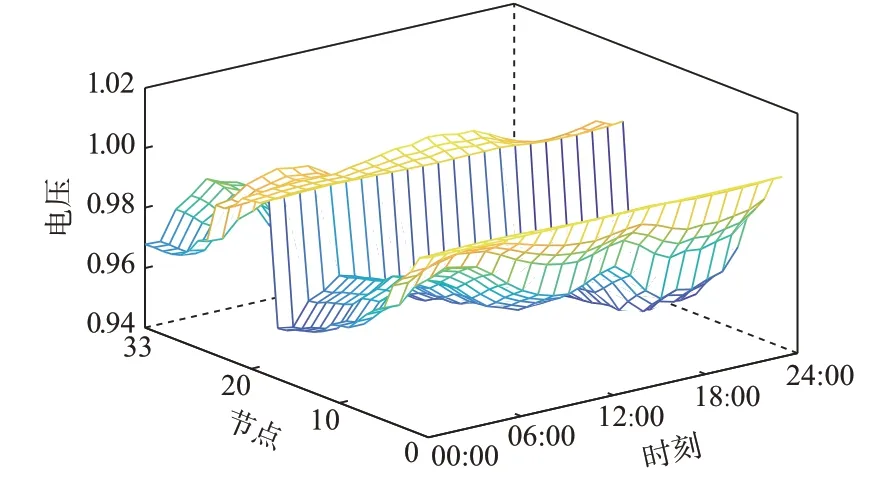
图4 接入MESS后各节点电压Fig.4 Node voltage with MESS accessed

MESS接入配电网后的削峰填谷效果如表5和图5所示。

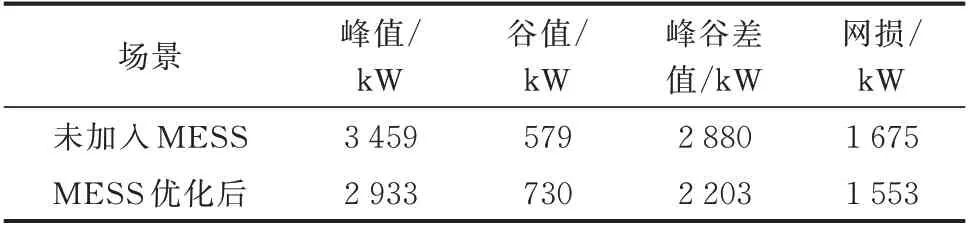
表5 削峰填谷效果对比Table 5 C omparison of peak load shifting effect

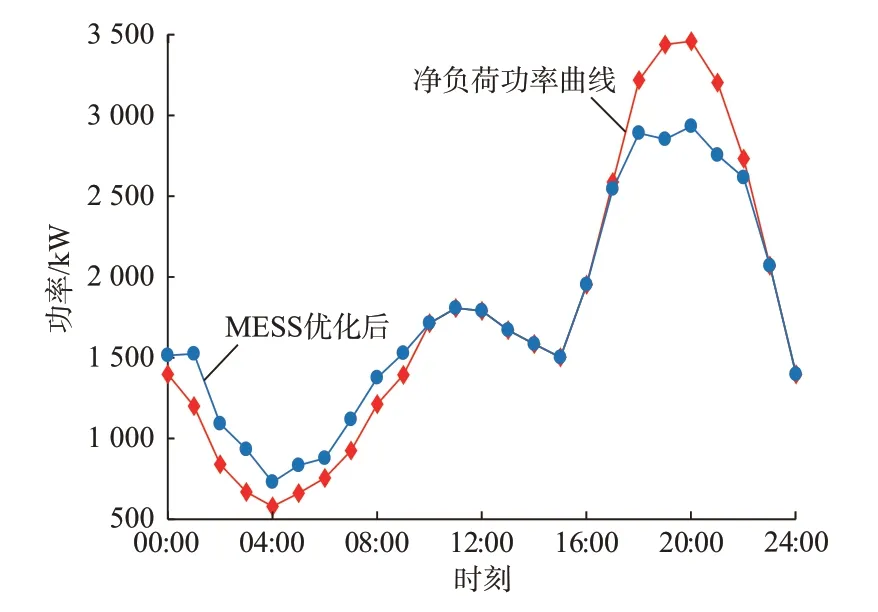
图5 MESS削峰填谷效果Fig.5 Effect of MESS in peak load shifting

可以看出,根据上述方法所求调度策略,优化后净负荷曲线的最大净负荷功率为2 933 k W,最小净负荷功率为730 k W,峰谷差减小为2 203 k W,负荷平均值为1 754 kW,网损减小为1 553 k W,MESS削峰填谷净收益为283元。对于其余未参与削峰填谷的MESS,其在削峰填谷应用场景下的能量转移为0,代入式（5）计算其经济效益为0。上述结果有效验证了所提调度方法的有效性,对于其余日负荷曲线,采用所提调度方法进行求解,若净收益为0或为负,则不必对MESS进行调度,故所提调度方法对不同负荷情况具有普适性。

4 结语

移动式储能在配电网削峰填谷方面具有广阔的应用前景,制定合理的削峰填谷调度策略是移动式储能商业化应用的关键。本文提出了一种基于改进EFWA的移动式储能削峰填谷调度优化方法,首先围绕MESS削峰填谷的可靠性、经济性以及减小网损建立了双层调度优化模型,并在IEEE 33节点配电系统中利用CPSO算法与改进EFWA进行求解验证,得到以下结论。

1）根据日前负荷预测数据,利用MESS削峰填谷调度目标函数可以实现MESS的调度优化,MESS双层优化模型可以求得所需的功率与容量,相应地选择合适参数的MESS,并派往不同的配电网节点提供充放电服务。

2）通过仿真验证了MESS可以兼顾削峰填谷可靠性与经济性的结论,MESS接入配电网,既能取得明显的削峰填谷效果,同时又能获得可观的经济效益。

3）对于削峰填谷下层高维非线性目标函数,基于高斯变异和柯西变异的改进EFWA所得结果优于CPSO算法和EFWA,证明了改进EFWA对于高维非线性问题求解具有很好的收敛性和精度。

本文所提调度策略仅在已有可调度MESS的条件下确定MESS的额定容量及接入位置,未考虑行驶路线对运行成本的影响,在后续工作中可考虑MESS削峰填谷的容量配置与路径规划。