基于分解协调方法的光储系统配置—运行协同优化

张雨曼，刘学智，兰 琛

（上海交通大学 电子信息与电气工程学院，上海 200240）

0 引言

光伏发电具有清洁、技术成熟等优点，构建以光伏—储能系统为基础的多能源系统，有利于提高光伏消纳、节省运营成本、缓解高峰用电压力。采用储能技术不仅可以平滑光伏系统输出，解决弃光问题，增强系统调频调峰能力，提高稳定性，还能够通过规划最佳的容量配置和充放电策略，为用户带来最大化收益［1］。将储能系统与光伏发电组合统筹规划，能够增强系统的可协调性和灵活性，为用户带来最大化收益。

由于光储系统的前期投入较大，因而对光储系统容量和功率的配置方案以及其经济效益的研究具有重要意义［2］。同时，对于光储系统调度的优化方案也对系统运行有借鉴意义［3］。文献［4］研究了分布式能源系统中的储能配置策略，文献［5］、文献［6］研究了含储能系统的运行调度策略，但是都只对配置或运行单独进行优化，并未将规划和运行统一进行优化。文献［7］综合研究了配置与运行优化，但是只有短时间尺度下的应用。文献［8］、文献［9］在多种时间尺度下进行了配置和运行的优化，但是均为建立指标对模型进行效益评估。

此外，基于全局优化的模型，需要同时决策光储系统的规划和运行，实现协同优化，导致求解难度大。Benders 分解法能将全局模型分解为主问题和子问题，在主、子问题局部优化的基础上达到全局最优，能够有效解决这类问题。文献［10］利用Benders分解将充放电状态和购售电状态的0/1变量和功率流动变量进行分解，得到了微网调度策略，但未实现规划运行协同优化；文献［11］利用Benders分解将综合能源系统分解为热力系统主问题和电力系统主问题，但也未涉及规划优化；文献［12］运用Benders 分解方法将复杂可再生能源接入规划问题分成投资—运行分解模型进行求解，但其只有单个典型日分析；文献［13］利用Benders分解将问题分解为初始投资费用主问题和运行优化子问题，但其子问题仅作为可行性检验，不会进行优化计算。现有的Benders 分解法大多缺乏多时间尺度的应用场景验证和经济技术效益的评估。

基于以上问题，本文在Benders分解模型的现有优势下探讨其衍生应用，利用Benders分解方法实现了光储系统配置—运行协同优化，将模型分解为规划配置主问题和运行调度子问题。计算中实现了Bender 割集累积过程的可视化，揭示了容量配置与优化运行的交互作用，直观展示出了Benders分解法的收敛过程，深入研究了Benders分解法在实际求解中的原理和过程，对分解协调优化模型之后的衍生应用有一定的借鉴价值。此外，探讨了分解协调优化模型在中长期尺度下求解的可行性，对于此方法在多时间尺度的应用也有参考意义。

本文首先建立光伏—储能系统规划和运行优化模型，建立目标函数，约束条件和评价指标；其次提出Benders分解方法对模型进行求解，并通过算例分析Benders 分解法的求解机理；最后提出聚类分析，基于3 个天气场景对全年光伏和负荷数据进行处理，建立全年的光伏储能模型，验证Benders 分解模型是否适用于长时间尺度的分析。

1 光伏—储能规划和运行优化模型

1.1 光伏—储能功率流模型

对应于储能电池的配置规划和光储系统的调度运行，本文决策变量定义如表1，对应的光伏—储能功率流动关系如图1。

图1 中，4 个实线功率流动变量是决策变量，2个虚线功率流动变量不是决策变量，但是其仍然存在，并且可以由其他决策变量表示。对于2 个虚线功率变量的处理如下:

表1 决策变量Table 1 Decision variables

图1 功率流动图Fig.1 Power flow diagram

（1）光伏售给电网功率PPV→grid

由于来自光伏系统的电力可以直接供给负荷、储能电池系统（BESS）或售给电网，因此必须满足以下约束条件

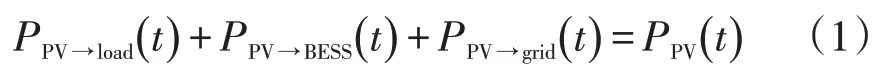
式中:PPV(t)为光伏发电量，是已知常数，因此与光伏有关的变量只有2 个为决策变量，即PPV→load(t)和PPV→BESS(t)，而PPV→grid(t)可以由这2个变量表示。

（2）电网购给负荷功率Pgrid→load

负荷功率要满足以下约束

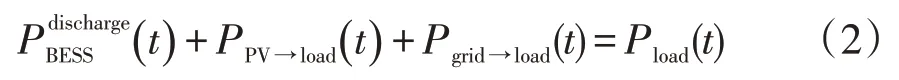
式中:Pload(t)为负荷量，是已知常数，因此与负荷有关的变量只有2 个为决策变量，即PPV→load(t)和而Pgrid→load(t)可以由这2个变量表示。

本文的负荷供电优先原则规定如下:

（1）当PPV(t)≤Pload(t)时，光伏发电量全部供给负荷，此时PPV→load(t)=PPV(t)。

（2）当PPV(t)＞Pload(t)时，剩余光伏电量可以选择储存到储能电池或者售卖给电网。此时PPV→load(t)=Pload(t)，剩余光伏功率PPV(t)-Pload(t)储存到储能电池。

对于剩余光伏功率的利用优先原则规定如下:

1.2 目标函数

设置目标函数为最小化的系统成本，由于光伏储能设备的维护成本较小，因此仅考虑运营成本Copex和投资成本Ccapex。

（1）运营成本

在t时刻，运营成本由电网购电支出、售电收入和光伏补贴组成。

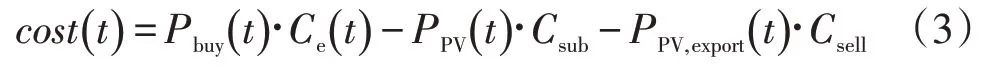
式中:cost(t)为t时刻的运营成本，由1 项运营支出（正值）和2项运营收入（负值）构成；Pbuy(t)为购电量；Ce(t)为购电价，对应购电支出；Csell为售电价，对应售电收入；Csub为光伏补贴价格，对应光伏补贴收入。

由此可得每日运营成本Copex为

（2）投资成本

由于本文是固定光伏出力的模型，光伏容量配置已确定，故不包含对光伏的配置优化，只关注储能电池的配置优化。因此，投资成本Ccapex分为储能电池容量成本Ccap和储能电池功率成本Cpower。

电池容量成本等于电池容量和单位容量投资成本之积［14］。设置锂电池放电深度为90%，则

式中:Smax为电池容量；unitcostcap为单位容量投资成本。

电池功率成本Cpower是满足功率要求的储能变流器（PCS）双向变流器成本（本文中PCS 变流器的超负荷率约为1.0），PCS 双向变流器功率与选取的电池最大充放电功率相同，电池功率产生的成本Cpower为变流器功率与单价的乘积，即

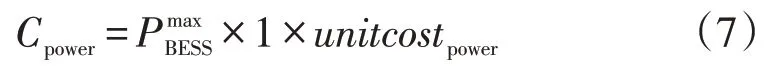
最终，投资总费用为

设置资金回收系数LFn，用于表示储能设备投资总费用均摊到储能设备寿命周期内每年的平均投资成本。

式中:d为折现率；n为储能电池的寿命年限。

综上所述，目标函数为一个典型日的总费用支出

1.3 约束条件

（1）电池充放电约束

任何时刻电池的充放电功率都应在额定范围之内，不应超出最大充放电功率

同时，由于频繁的同时充放电会缩短电池寿命，因此规定储能电池的充电和放电不能同时进行，即

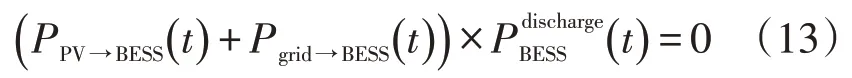
（2）光伏出力约束

（3）负荷功率约束

（4）电池容量约束

当电池在充放电过程时，电量满足约束

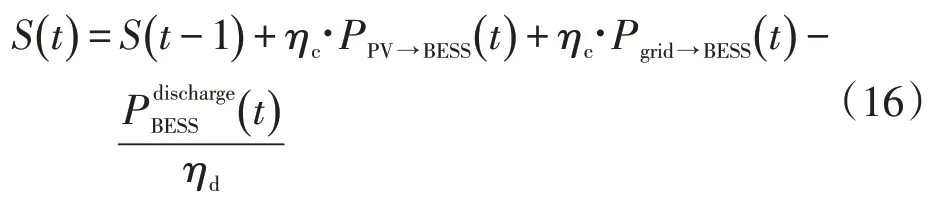
其中ηc=ηd=0.98，是电池充放电效率。t时刻的电池电量为t-1 时刻的电量加上这1 h的充放电电量。显然，电池容量S(t)不能超过额定容量，即

（5）电量置零约束

在电池容量约束的基础上，考虑储能电池一天24 h充放电总量的累积和为0，即

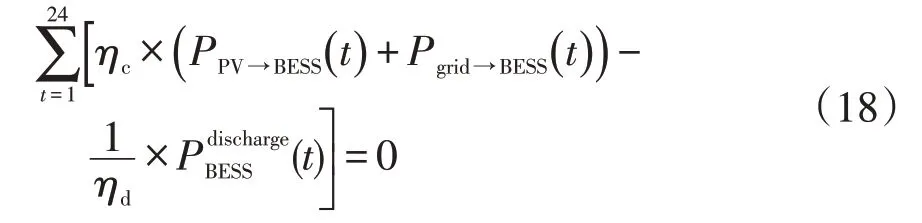
（6）电池充放电次数约束

电池充放电次数过多，可能导致电池提前老化，降低电池的使用寿命。为了让电池健康工作，我们需要对电池的充放电次数进行约束，使电池一天中放电总量不超过电池容量，这意味着一天中电池进行不超过一次放电循环。

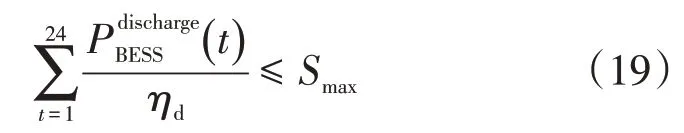
1.4 评价指标

为了评价模型的优劣，对优化结果进行指标的计算。本文的评价指标包括光伏自我消纳率（self-consumption ratio，SCR）和自给率（self-sufficiency ratio，SSR），净现值（net present value，NPV）和内部收益率（internal rate of return，IRR），动态投资回收期。

1.4.1 消纳率与自给率

储能电池可以显著提高消纳率和自给率。

消纳率定义为光伏系统产生的供给负载和储存电池的能量（EPV,used）与产生的总能量（EPV,gen）之比

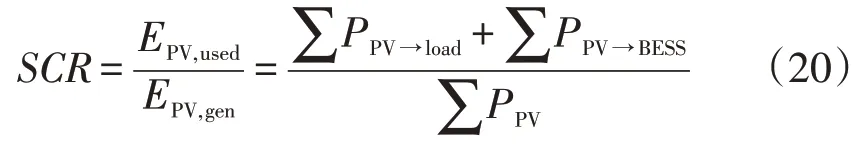
自给率定义为光伏系统产生的供给负载和储存电池的能量（EPV,used）与负载使用的能量Eload之比

1.4.2 净现值和内部收益率

净现值是一项投资所产生的未来现金流的折现值与项目投资成本之间的差值，反映了项目投资获利能力的指标。一般情况下，净现值大于0时，该项目是可行的。

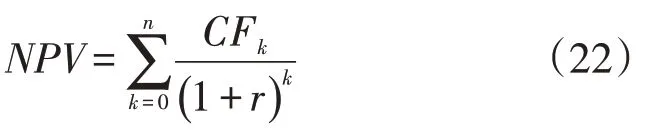
式中:CFk为每年的净现金流量，即每年电池售电收入和该年的所有支出之和；r为贴现率。

内部收益率定义为电池净现值为零时的折现率。一般情况下，IRR大于等于基准收益率（6%）时，该项目是可行的。

可以通过求解NPV=0 来确定内部收益率，如下所示

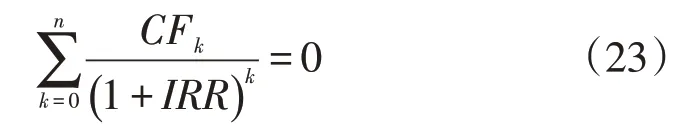
1.4.3 动态投资回收期

动态投资回收期是指在考虑货币时间价值的条件下，以投资项目净现金流量的现值抵偿原始投资现值所需要的全部时间。

计算方式为:由光伏储能系统的售电收入与光伏补贴之和，减去购电成本，得到系统的总运行收益。当系统运行到第n年时，累计总运行收益超过初始投资成本Ccapex。表达式如下所示

式中:Cin(k)为第k年的运行收入；Cout(k)为第k年的运行成本；r为贴现率。当计算所得的n大于电池寿命时，投资无法回本，更无法盈利。

2 基于Benders分解的光伏—储能规划和运行优化模型

2.1 Benders算法

Benders 分解算法是 J.F.Benders 在 1962 年首先提出的，目的是用于解决混合整数规划问题，即连续变量与整数变量同时出现的极值问题。但它的实际应用并不限于此，它可以对具有Benders分解基本形式的非线性问题求解［15］。

其通用数学公式为

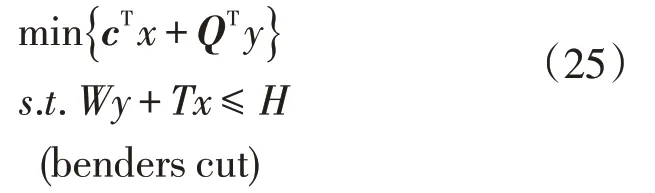
式中:x为主问题变量；cT为x的变量系数矩阵；y为子问题变量；QT为y的变量系数矩阵；（benders cut）为割集。通过将主、子问题分解，相互迭代求解全局最优值，其求解流程如图2所示。

值得注意的是，子问题在反复迭代的过程中形成的可行割或不可行割是不断累积的，最终会形成一个割集，对主问题进行约束。随着迭代进行，割集不断增大，可行解不断减少，使得问题最终趋向最优解。

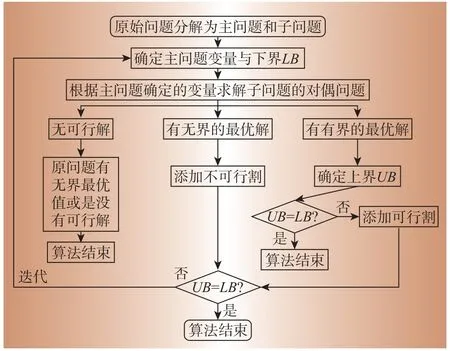
图2 算法流程图Fig.2 Algorithm flow chart

2.2 变量参数化

为了便于使用Benders算法优化，本文在进行问题分解时，将配置问题确定为主问题x，运行问题确定为子问题y。由此，将电池容量Smax和电池最大额定充放电功率用参数x(1)和x(2)表示，t时刻光伏供给负荷的功率PPV→load(t)，光伏供给储能电池 功 率PPV→BESS(t)，电网供给储能电池的功率Pgrid→BESS(t)，储能电池放电功率分别用参数y(4t-3)、y(4t-2)、y(4t-1)、y(4t)表示，如表2所示。

表2 参数设置表Table 2 Parameters setting table

2.3 建立参数化系统模型

2.3.1 目标函数

将变量参数化后，最终的目标函数方程为

由于Benders中目标函数方程为

对应得到主问题x的变量系数矩阵c和子问题y的变量系数矩阵QT

2.3.2 约束

本文模型中的变量系数矩阵形式为线性形式Wy+Tx≤H。对应该形式，将在1.3 节中设立的约束方程参数化:

电池放电约束

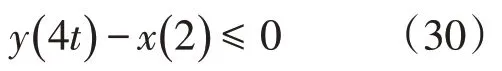
电池充电约束

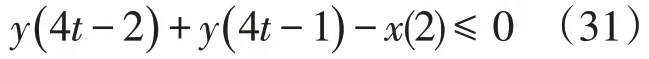
光伏出力约束

负荷功率约束

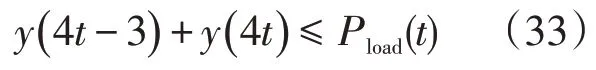
电池容量约束1

电池容量约束2

量置零约束

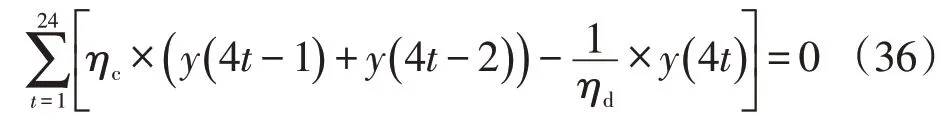
电池充放电次数约束

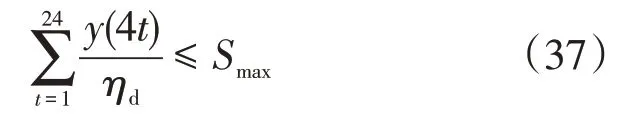
以上参数化约束条件方程对应的矩阵表达如表3。

为了将不等式约束转换为等式约束，引入松弛变量组成稀疏矩阵Asparse，由于改造的不等式约束都是同号（≤），所以松弛变量的系数都是1，矩阵近似单位矩阵，只有等式约束对应行为零元素。

y的新变量系数矩阵W′由W和Asparse组成如下

2.4 算例求解

本文采用的是广东某工业园区数据，主要考虑包括华夏学院等在内的5家用户的负荷，并使用2020年低方案负荷数据。由于本文研究用户属于工业用电，负荷曲线与该工业园区本身的运行安排相关，如图3（a）。在13:00出现负荷率最低点的原因是由该工业园区生产排班所造成。光伏数据见图3（b），24 h分时电价如图3（c）。光伏上网电价Csell= 0.451 5 元/kWh ，光伏补贴Csub= 0.42 元/kWh，折现率d= 0.06，储能电池充放电效率η= 0.98，电池容量投资成本unitcostcap=125 万元/MWh ，电池功率投资成本unitcostpower=50 万元/MW ，储能电池的寿命年限n=11［16］。

表3 变量系数矩阵Table 3 Variable coefficients matrix

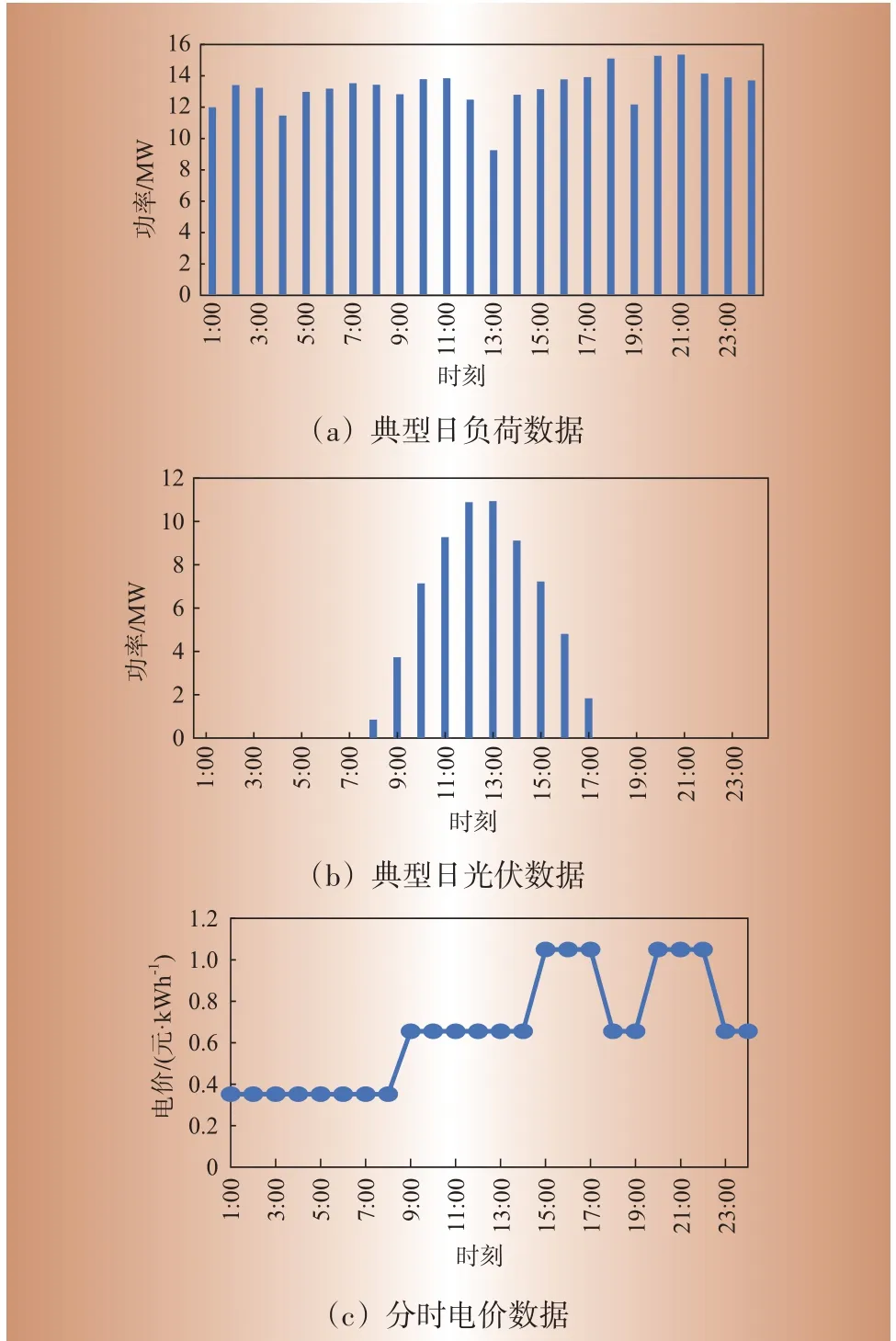
图3 广东某工业园区数据Fig.3 Data of an industrial area in Guangdong

2.4.1 Benders算法迭代过程

在MATLAB 程序中经过多次迭代后，生成的割平面如图4所示。图4实现了迭代计算时Benders割集形成过程的可视化，可以直观看出割平面的累积过程，即割集的形成。从求解结果可知，在计算过程中发生了9 次迭代并产生了9 个割平面，每次迭代都会为算法增加切割和新约束。

最小日成本、最大充放电功率及最大电池容量的随着迭代进行的收敛过程如图5所示。前4次迭代数值巨大，故省略。由图5可知，随着迭代不断进行，在第六次迭代后各优化目标已趋于收敛，在第九次迭代后找到最优结果。

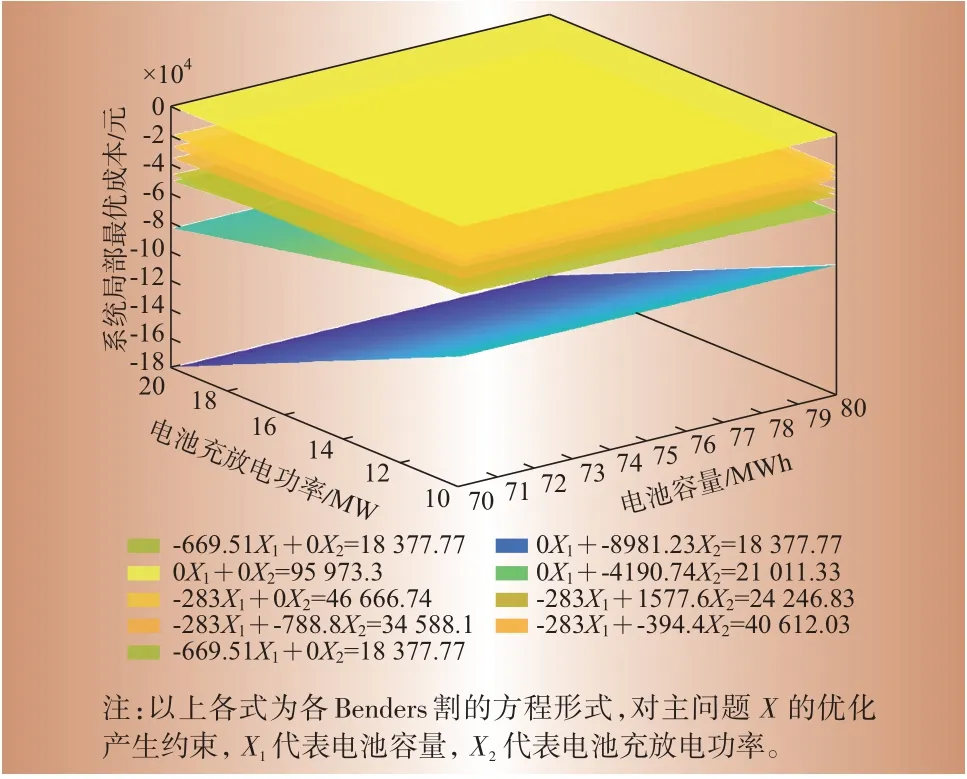
图4 优化空间和割平面Fig.4 Optimize space and benders cut plane

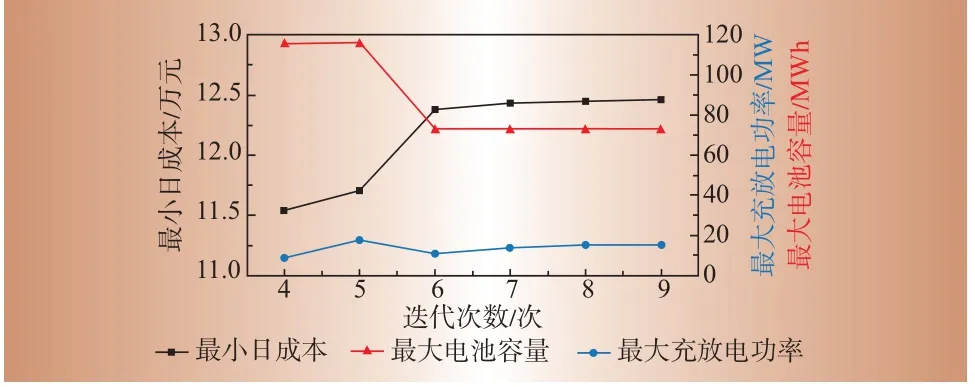
图5 迭代收敛过程Fig.5 Iterative convergence process

2.4.2 配置及运行优化结果分析

配置和运行优化结果如表4，在这样的储能电池配置下，系统运行调度情况如图6所示。

表4 优化结果Table 4 Optimization results

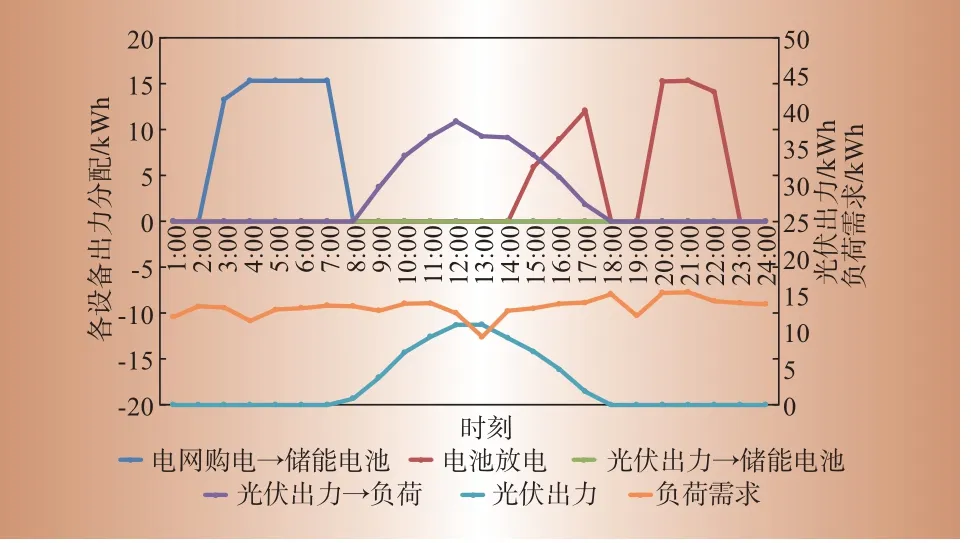
图6 光伏—储能系统运行调度优化结果Fig.6 Scheduling optimization results of photovoltaicbattery system

由计算得出的经济指标可以看出，其均满足以下3 个要求:一是净现值大于0；二是内部收益率大于或等于基准收益率（6%）；三是动态回收期效于电池寿命（11 年）。因此是具有经济效益的可行方案，具有现实意义。

3 基于聚类—Benders 分解的中长期光伏储能系统

为探究本文方法是否适用于长时间尺度上的案例，利用K-means 聚类算法对长时间尺度上的光伏出力数据进行聚类分析，建立全年的光伏储能模型，验证其可行性［17］。

3.1 基于K-means聚类分析的全年光伏储能系统分析

第二章的典型日光伏储能系统案例分析是基于典型日24 h光伏出力和负荷需求的数据，但光伏出力数据在长时间尺度上可能会因为各种因素产生波动和差异，为了探究第二章的优化结果是否适用于长时间尺度上的案例，要利用K-means 聚类算法对长时间尺度上的光伏出力和负荷数据进行聚类分析，建立全年的光伏—负荷出力模型。

本节对全年8 760 h 的光伏出力和负荷数据中每个月的数据利用K-means 聚类分析，通过设定K=3，将聚类分析所得数据对应到3种天气情况，即晴天、阴天和雨天。

12个月份的光伏和负荷的聚类结果分别计算如图7、图8所示。

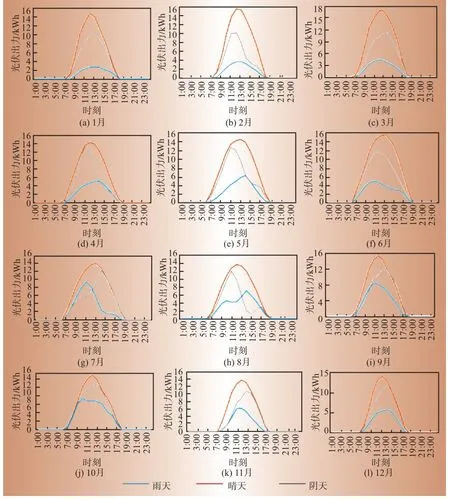
图7 1月至12月光伏聚类结果Fig.7 PV clustering results from January to December

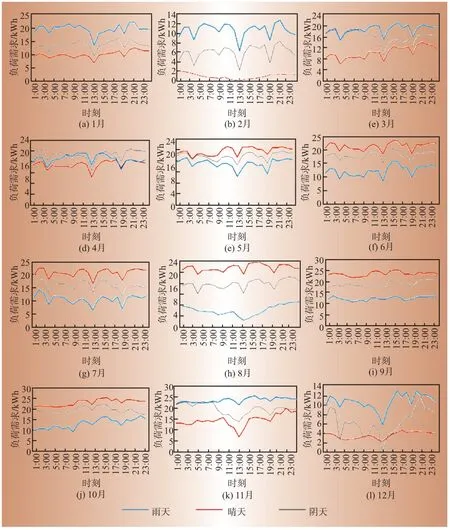
图8 1月至12月负荷聚类结果Fig.8 Load clustering results from January to December

关于3种天气情况的聚类结果如表5所示。

表5 每月聚类结果Table 5 Clustering results of each month d

为了生成全年的总成本表达式作为目标函数，设置第m月的3 种天气情况的天数分别为:晴天天数为Dsunny(m) ，阴天天数为Dcloudy(m) ，雨天天数为Drainy(m)。第m月的晴天运营成本为Copex,sunny(m)，阴天运营成本为Copex,cloudy(m) ，雨天运营成本为Copex,rainy(m)，则全年的总成本可以表示为

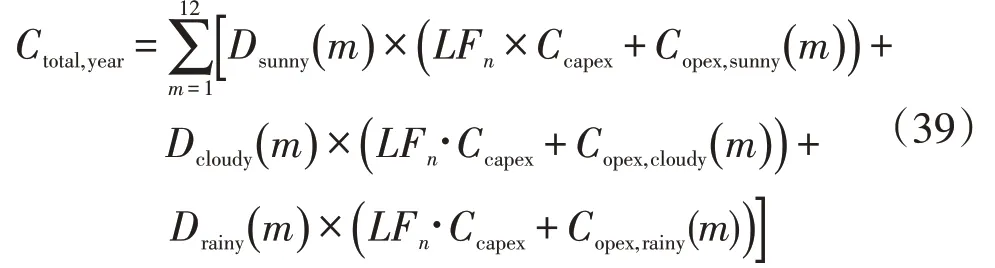
对于约束条件，中长期优化模型以12个月的典型日为优化对象，以一年12个月的年度总成本为优化目标，本质上研究对象仍然为典型日，因此其仍然采用第二节模型的约束，未添加新的约束。

由此，基于K-means 聚类分析的中长期优化配置与运行模型建立完成。

3.2 全年光伏—储能系统优化结果

将聚类分析所得年光伏出力模型，同样利用Benders 求解法计算。最大充放电功率及最大电池容量的随着迭代进行的收敛过程如图9所示。最优配置下的优化结果如表6所示。

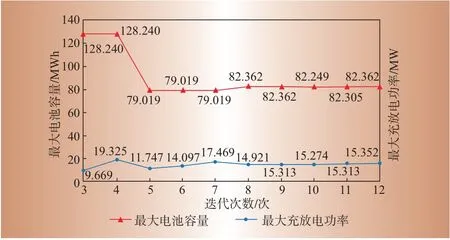
图9 迭代收敛过程Fig.9 Iterative convergence process

表6 中长期尺度下配置和运行方案Table 6 Configuration and operation plan under the medium and long-term scale

4 结束语

本文主要是利用Benders 分解算法对长时间尺度上的光储系统模型进行优化求解，确定储能电池的最优配置和系统的优化调度方案。

为建立光储系统模型，首先明确了光储系统内部的功率流，确立优化求解最重要的目标函数，并依据功率流动和储能电池状态设立模型的约束条件，然后选取了消纳率、自给率、净现值等用于评估优化结果的指标。然后依据Benders算法思想，将问题分解为配置主问题和运行子问题，将原有模型进行参数化，配合线性规划函数经过多次迭代求解出储能电池的最优配置和系统的优化调度方案。此外，本文使用了K-means 聚类分析算法对长时间尺度（全年）的光伏出力和负荷数据进行聚类分析，建立全年的光储优化模型，并仿效之前的求解过程进行优化求解，得出长时间尺度的优化配置方案。

总的来说，本文展示了算例求解中Benders分解法的迭代过程，以及Benders 割的形成机理和过程，对于分解协调模型求解原理实现了更深刻的剖析，对Benders 分解法之后的衍生应用有一定的借鉴价值。此外，本文加入全年的光储优化模型，验证了Benders分解法在长时间尺度下求解的可行性，对于此方法实现在多时间尺度的应用也有参考意义。