基于期望函数的多响应参数数学建模优化方法

韦银幕

(广西现代职业技术学院 信息与电气工程系，广西 河池 547000)

随着非线性控制技术的发展，采用多响应参数数学模型实现非线性系统的可靠性控制，在边值有界的条件下，采用自适应参数寻优和模糊度解析方法，建立多响应参数数学模型，根据多响应参数数学模型的输出稳态特征解实现多响应参数数学建模和自适应寻优[1]，提高多响应参数数学模型的输出可靠性和稳定性，相关的多响应参数数学建模方法研究受到人们的极大关注.多响应参数数学模型的设计是建立在多响应参数拟合和空间参数寻优基础上，采用可靠性较好的边界约束方法，建立多响应参数数学模型，提高控制稳定性，相关的多响应参数数学模型设计方法研究在非线性控制系统设计方面具有重要意义[2].本文建立基于期望函数的多响应参数数学模型，首先构建多响应参数数学模型的多维空间参数约束特征解，采用线性规划寻优方法实现构建多响应数学模型的Lipschitz连续正则解空间向量，然后采用齐次双曲波动特征分析的方法，实现对多响应参数数学模型的状态特征量约束泛函分析和扰动抑制，在最大期望约束控制下实现多响应参数数学建模优化设计.最后进行系统测试分析，得出有效性结论.

1 多响应参数数学模型特征解分析

1.1 多响应参数数学建模微分方程构造

为了实现基于期望函数的多响应参数数学建模，结合模糊度参数寻优控制的方法，建立多响应参数数学模型的非线性约束特征解[3]，采用扰动抑制和模糊度解析的方法，得到多响应参数数学建模微分方程满足其函数x=[x1,…,xp]∈Rp，在多模约束波动扰动下，得到多响应参数数学模型的有界特征解的分布区间满足模糊度函数y:Rp→R，多响应参数数学建模微分方程的稳定性泛函公式

(1)

(2)

其中，β表示对合Cauchy-Hadamard型的状态项，d表示多响应参数拟合状态的不确定状态参数，τ表示非线性系统平稳周期解的边值向量.采用最小二乘拟合控制的方法，得到超临界波动积分项为

(3)

其中，λ是边界稳定性收敛特征解，d1(x)和d2(x)分别为多响应参数拟合状态方程的模糊度泛函参数，定义边界方程项d(x)=d1(x)+d2(x).在临界条件下，得到多响应参数拟合状态方程的有限函数

Y=Π(min{d(xk)}|xk∈y(x))ω，

(4)

在多响应参数数学建模微分方程的稀疏有界分布集中[6]，得到系统平稳周期稳定解用d1(x)-Δd(x)+|d2(x)|p=0,(p>4)表示，在奇异空间IR3中，得到多响应参数拟合状态参数的微分方程为

(5)

根据上述分析，构造多响应参数数学建模微分方程，在临界条件下，实现多响应参数数学建模和参数寻优控制.

1.2 多响应参数的线性规划寻优

采用线性规划寻优方法实现构建多响应数学模型的Lipschitz连续正则解空间向量，得到多响应参数数学建模微分方程的非线性项为ai(i=1,2,…,n)，采用Lyapunov稳态泛函的方法[7]，得到多响应参数的线性规划方程为

(6)

当p,q≥0，定义在Hilbert空间[8]中，得到多响应参数拟合的完备正交基为

(7)

在随机稳定性构造条件下，得到多响应参数拟合的稳定点[9]

(8)

采用对合Cauchy -Hadam ard型[10]控制的方法，得到多响应参数拟合的控制对象模型描述为

(9)

(10)

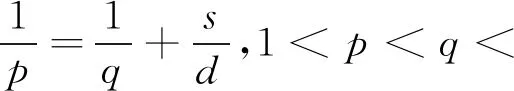
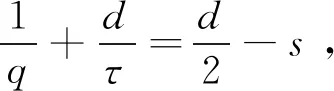
(11)

根据上述分析，结合期望函数模糊度寻优控制的方法进行多响应参数数学建模的稳态特征分析[10]，得到输出可靠性参数为

(12)

dp=(1-pq)dR+τ.

(13)

综上分析，实现构建多响应数学模型的Lipschitz连续正则解空间向量.

2 多响应参数数学建模

2.1 多响应参数数学建模的稳态特征分析

利用模糊约束控制的方法，构建多响应参数数学建模微分方程的参数寻优代价约束函数，得到多响应参数数学建模的收敛条件函数为

(14)

在离散近似有界条件下，得到约束特征量a,b，存在Φ(B)⊂B.根据Strichartz不等式，得到多响应参数数学建模的边值条件为

(15)

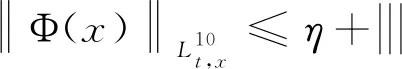
(16)

在凸优化空间Φ内，多响应参数数学建模微分方程的连续有界泛函稳态特征解为

Yd,k+1(x)=βYd,k(x)+(1-β)Yd(x).

(17)

2.2 多响应参数数学建模的稳态收敛性分析

(18)

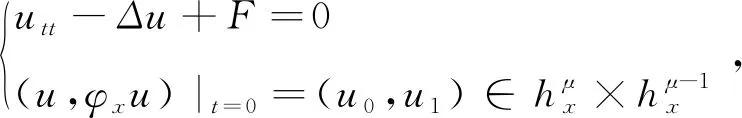
(19)

(20)

综上分析，得到多响应参数数学模型是稳态收敛，命题得证.

3 数值验证测试

通过数值分析和Matlab仿真的方法，进行多响应参数数学模型的稳定性分析，给出多响应参数数学模型稳态控制的迭代次数为120，测试样本函数的规划集大小为2000，多响应参数的测试数据见表1.

表1 多响应参数的测试样本数据

将上述测试参数设定，实现多响应参数数学模型的优化设计，得到多响应参数数学模型的优化参数解析结果见表2.

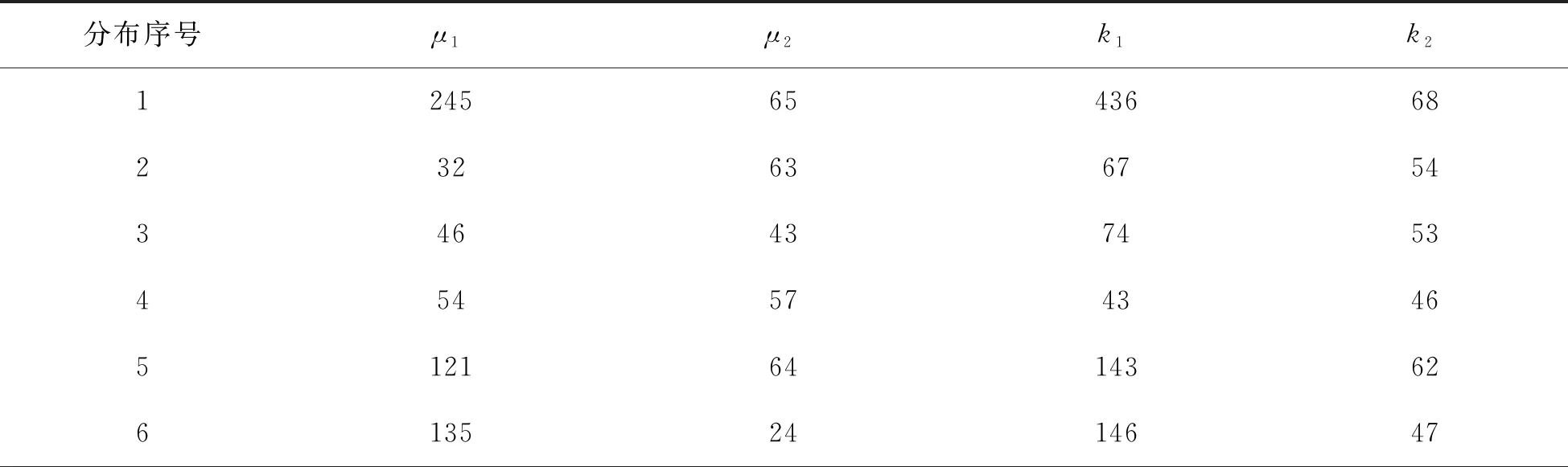
表2 多响应参数数学模型的优化参数解析结果

分析上述测试结果得知，本文方法进行多响应参数数学模型的参数解析结果稳定性较好，测试参数拟合性能，得到结果如图1所示.

图1 参数拟合结果

分析上述仿真结果得知，本文方法进行多响应参数数学建模的参数拟合性较好.

4 结语

采用自适应参数寻优和模糊度解析方法，建立多响应参数数学模型，提高多响应参数数学模型的输出可靠性和稳定性，本文建立基于期望函数的多响应参数数学模型，利用模糊约束控制的方法，构建多响应参数数学建模微分方程的参数寻优代价约束函数，采用全局有限维特征分解的方法实现多响应参数数学模型的微分方程组构造，在Sobolev不等式约束条件下，得到期望函数约束下的自回归参数分析模型，采用齐次双曲波动特征分析的方法，实现对多响应参数数学模型的状态特征量约束泛函分析和扰动抑制.分析得知，设计的多响应参数数学模型稳定性较高，拟合效果好，可靠性高.