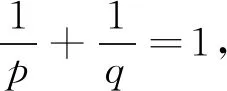常p -Laplacian系统周期解的存在性
郭 曼,王大斌
(1.四川信息职业技术学院 基础教育部,四川 广元 628000;2.兰州理工大学 理学院,甘肃 兰州 730050)
考察如下p-Laplacian系统

(1)
当p=2时,系统(1)即为二阶Hamiltonian系统.经查阅文献发现,对于二阶Hamiltonian系统解的存在性问题,大量学者采用了不同的方法来验证,最后得到了一系列成果.特别地,Li[1]等在较弱的积分周期条件下得到了关于系统(1)周期解的一个新的结果,且该结果推广了Willem[2]的结论.通过采用类似于文献[1]中的条件,Wang[3]等证得了二阶离散Hamiltonian系统存在周期解.其他研究成果详情可参见文献[4-8]及其参考文献.
目前,关于(1)式这样的p-Laplacian系统周期解的存在性问题受到了很多学者的关注,详情可见文献[9-14]及其参考文献.特别地,文献[9]分别运用对偶最小作用原理和鞍点定理讨论了系统(1)周期解的存在性问题,并且最后在该问题上有所收获.
受到文献[1]和[9]的启发,一个自然的问题:若用[1]中的方法去研究[9]中的系统的周期解存在性问题得到几个结论.
1 主要结论
本文主要针对系统(1)的周期解的存在性问题展开讨论,其中p≥2,F:×N→,N≥2,F(t+T,x)=F(t,x),T>0,F(t,u(t))=F′(t,u(t))表示F(t,u(t))关于t的梯度.在文中,假定F(t,u(t))满足如下条件:
(A)对任意x∈N,F(t,x)关于t是可测的,对几乎每个t∈[0,T],F(t,x)关于x连续可微,且存在a∈C(+,+),b∈L1([0,T];+),对每个x∈N和几乎所有的t∈[0,T]满足下列式子
|F(t,x)|≤a(|x|)b(t),|F(t,x)|≤a(|x|)b(t).
下面为本文的主要结果.
定理1假设F满足条件(A)和下列条件
(F1){ei|1≤i≤n}是N的正交集,存在Ti>0对任意的x∈N和几乎所有的t∈[0,T]满足


|F(t,x)|≤C1|x|p+C2,
则系统(1)至少存在一个T-周期解.
定理2假设条件(A),(F1)和下列条件成立
(F3)存在λ1 (F4)当|x|→+,对任意的t∈,存在δ>0满足F(t,x)>δ, (F5)F(t,x)≤b|x|p. 定义空间 引理1[16]假设X为Banach空间,f∈C1(X,).若{un}⊂X满足如下条件 f(un)→C,(1+‖un‖)‖f′(un)‖*→0, 且{un}⊂X存在收敛的子序列,则泛函f满足(CPS)C条件. 引理2[17]X为自反的Banach空间当且仅当X中任一有界序列存在弱收敛的子序列. 通过运用文献[2]中的方法,得到了如下结果. (i)Poincare-Wirtinger不等式 (ii)Sobolev不等式 ‖u‖ 引理4[2]假设X为Banach空间,M⊂X为弱闭子集,且f:M→∪{+}为弱下半连续函数.若f在M上的极小化序列有界,则f在M上可达到下确界. 引理5[2]假设X为自反的Banach空间且f∈C1(X,).令X=X1⊕X2且 dimX1<+, 令 引理6[18-19]假设L:[0,T]×N×N→对任意的(x,y)∈N×N,L(t,x,y)关于t是可测的,对几乎所有的t∈[0,T],L(t,x,y)关于(x,y)是连续可微的,且存在a∈C(+,+),b∈L1([0,T];+)和c∈Lq([0,T];+),1 |L(t,x,y)|≤a(|x|)(b(t)+|y|q),|DxL(t,x,y)|≤a(|x|)(b(t)+|y|q), |DyL(t,x,y)|≤a(|x|)(c(t)+|y|p-1), 在Sobolev空间 内是连续可微的,且有 易知,泛函f的临界点对应系统(1)的周期解. 定理1的证明 事实上, 由Poincare-Wirtinger不等式和(F2)可得 (2) 因此,f在X上是强制的. (3) 由假设(F1)可以推出 因此,若{uk}为f的极小化序列,则 也为f的极小化序列.所以,可以假设 (4) 结合(3)和(4)可得{uk}为一有界极小化序列.因此,存在弱收敛的子列.此外,由于f是凸连续函数和弱连续函数之和,可得f是弱下半连续的.结合引理6,结论成立. 注1定理1推广了文献[1]中的定理1.3,利用鞍点定理,得到了关于周期解的新的存在性定理,其中文献[1]中的p=2. f(uk)→C,(1+‖uk‖)‖f′(uk)‖*→0, 从而对任意的n∈,有 |f(uk)|≤C,(1+‖uk‖)‖f′(uk)‖*≤C. (5) 结合(5)和(F3),得到 (p+1)C≥(1+‖uk‖)‖f′(uk)‖*-pf(uk) ≥〈f′(uk),uk〉-pf(uk) 这意味着,存在常数C使得 由(5)可知 即 (6) 由假设(F1)可以推出 因此,若{uk}为f的一(CPS)C序列,则 也为f的(CPS)C序列.所以,可以假设 (7) (8) uk→u在C([0,T];N)中. (9) 结合文献[14]中的结果,便有 ‖uk‖→‖u‖. (10) 定理2的证明 另外,对任意的u∈X1,由(F4)得 则利用引理7和引理5,可以得到系统(1)存在一个T-周期解. 注2定理2推广了文献[1]中的定理1.4,而且本文结论不同于其他文献证得的结果. 注3定理2中的条件(F3)弱于定理1中的条件(F2).
2 预备知识







3 主要结论的证明