基于截断奇异值的镜像综合孔径亮温重建方法

吴袁超 吕容川* 窦昊锋 李一楠 李 浩卢海梁 罗 丰 李青侠

①(中国空间技术研究院西安分院 西安 710000)

②(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

③(华中科技大学电子信息与通信学院 武汉 430074)

1 引言

微波辐射测量技术最早被用于射电天文领域，目前在地球遥感、医学及目标探测方面有越来越多的应用。光学、红外遥感虽然具有较高的空间分辨率，但存在易受天气因素(云、雨、雾等)干扰的缺点。微波遥感由于其能实现全天时、准全天候的实时动态遥感监测，而受到广泛关注[1]。为提升微波辐射计的空间分辨率，综合孔径技术被引入到微波辐射计中，其采用多个小口径天线合成等效的大口径天线，通过直接测量的可见度函数经傅氏变换得到重建亮温图像。但相比于实孔径辐射计，综合孔径系统天线单元与通道数量多，数据处理相对复杂很多。综合孔径辐射计是以系统电气的复杂性与信号处理的复杂性换取实孔径辐射计中的机械复杂性[2,3]。对于空间分辨率要求较高的综合孔径辐射计，例如GeoSTAR，其需要几百个天线和接收通道，上万个相关器，导致系统装配困难、成像复杂度高。

为进一步提高微波辐射计的空间分辨率，文献[4–7]提出了镜像综合孔径(Mirrored Aperture Synthesis, MAS)的概念。镜像综合孔径辐射计采用反射板与天线阵组合，形成等效的镜像阵列，通过求解转移方程获得余弦可见度函数，由余弦可见度函数经反余弦变换可获得重建亮温图像。相较于常规综合孔径辐射计，镜像综合孔径辐射计能够在相同阵列大小下，有效提高系统的空间分辨率[8,9]。由于实际系统硬件等因素影响，测量数据不可避免地存在误差与噪声。并且，对于镜像综合孔径辐射测量而言，余弦可见度函数由转移方程求解得到，求解的精度将影响最终重建亮温的精度。然而，转移矩阵为病态矩阵，含有误差的相关输出与病态的转移矩阵求解得到的余弦可见度偏离了正确的解向量，导致最终的重建亮温图像失真。

本文将基于镜像综合孔径的基本原理，研究一种镜像综合孔径的亮温重建方法——截断奇异值分解，用于改善镜像综合孔径的成像质量。并通过仿真与实验验证该方法的有效性。

2 镜像综合孔径的基本原理

如图1所示，镜像综合孔径辐射计由反射板与天线阵组成。阵列中任意天线单元将接收来自场景的直射信号与来自反射板的反射信号。

当接收天线的极化方向为x方向时，天线p和q接收到的信号的相关输出为

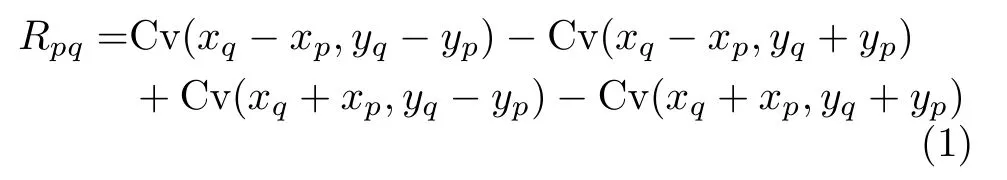
其中，( xp,yp)与 ( xq,yq)分别是波长归一化的天线坐标，C v(u,v)是2维余弦可见度，可表示为

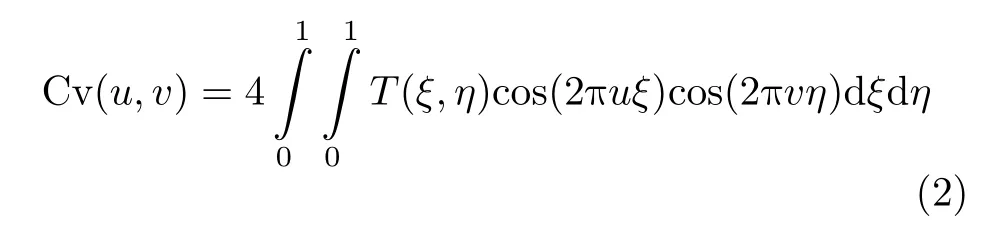
镜像综合孔径的双天线相关输出与余弦可见度可线性表示为

其中，式(3)即为转移方程。Q表示天线单元数目，M和N分别表示两个维度的最大空间采样频率。R为双天线相关输出向量，P为转移矩阵，CV为余弦可见度向量。

亮温与余弦可见度间的余弦变换关系为

故镜像综合孔径的重建亮温是先由式(3)求解得到余弦可见度，再根据式(4)进行反余弦变换得到。

3 转移矩阵的病态性

由双天线相关输出求解余弦可见度为一个数学反问题，求解反问题需要考虑其不适定性。而式(3)是一个第1类Fredholm的离散模型的方程组形式，是一个典型的病态方程，其解是不稳定、不唯一的，即式(3)是不适定的。若采用广义逆求解式(3)

其中，P+为转移矩阵P的广义逆矩阵。当相关输出存在任何微小的误差或噪声时，求解得到的余弦可见度结果将很不稳定，含有很大误差，严重偏离正确值。而镜像综合孔径的重建亮温是由余弦可见度经过余弦变换得到，余弦可见度的误差将导致重建亮温图像的失真。图像误差可以用误差条件下的重建亮温与理想条件下的重建亮温Tid的均方根值来衡量

其中，M代表像素点数。

以一个24单元的双L阵列为例，仿真存在系统噪声时，镜像综合孔径的成像效果。系统带宽设置为200 MHz，积分时间为0.05 s，接收机噪声温度为500 K。余弦可见度函数由式(5)求解得到。双L阵列如图2所示。仿真场景为环形展源(模拟电暖器实验场景)，理想的重建亮温结果如图3所示。加入系统噪声后的重建亮温图像如图4所示。从仿真结果可以看出，加入系统噪声后，重建亮温图像背景不均匀，且目标轮廓扭曲，图像质量不佳，图像误差ΔT = 103 K。

图4的结果主要是由于受误差影响，转移矩阵P的条件数“很大”，得到的余弦可见度含有较大误差。

假设转移矩阵P稳定不变的情况下，由矩阵论[10]，有

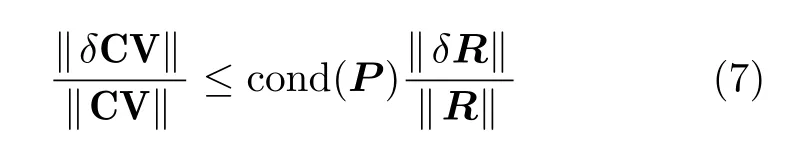
图2 双L阵列

其中，||δR||表示相关输出向量R的噪声，||δCV||为由||δR||导致的余弦可见度CV的误差，cond(P)为转移矩阵P的条件数，记为其中，σmax为转移矩阵P的最大奇异值，σmin为转移矩阵P的最小奇异值。

条件数可用于衡量误差或噪声经转移矩阵P到余弦可见度CV的扩大程度。当 cond(P)趋近于1时，相关输出向量R或转移矩阵P的一个较小扰动只引起余弦可见度CV的一个很小扰动，此时转移矩阵P为良态矩阵，否则，就称为病态矩阵。并且，条件数越大，矩阵的病态性也越大。

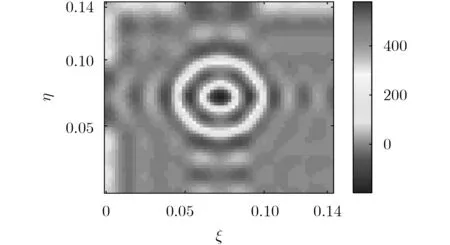
图3 理想重建亮温图像

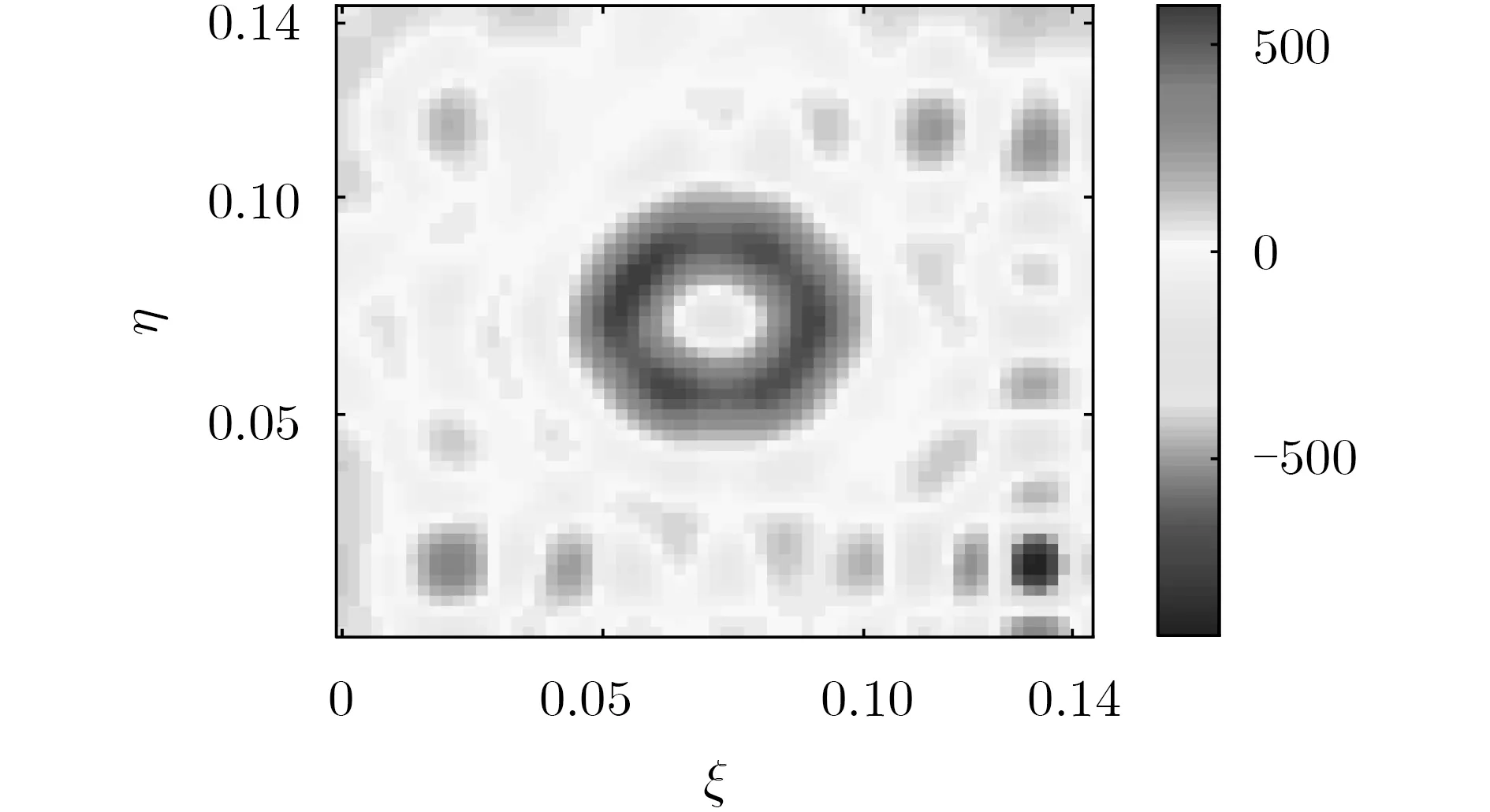
图4 带系统噪声的重建亮温图像

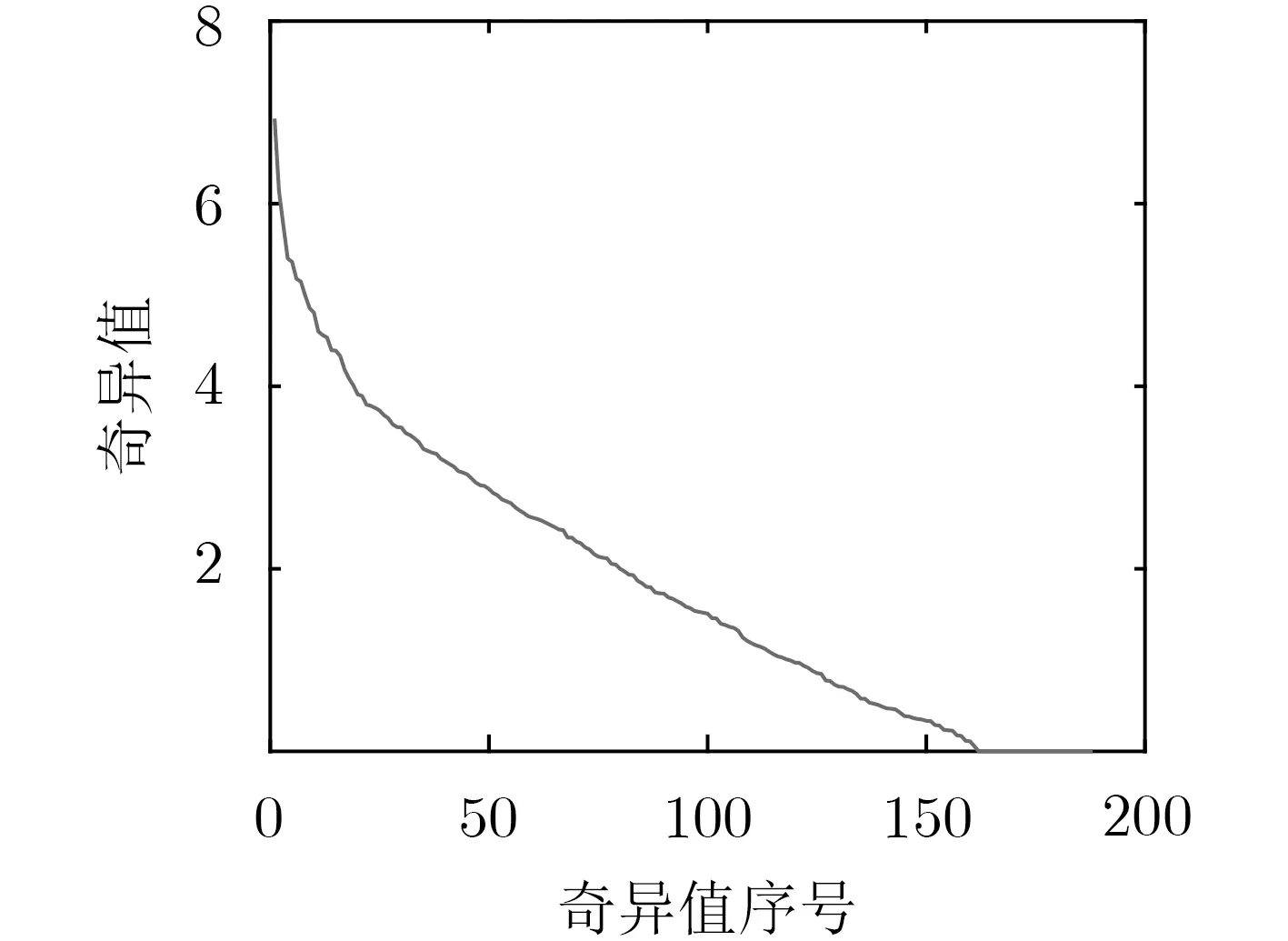
图5 转移矩阵P 的奇异值

双L阵对应的转移矩阵P的奇异值如图5所示。可以看到，其奇异值从第162号开始均为0，即σmin=0。由式(7)可知，此转移矩阵P的条件数为无穷大，转移矩阵P是相当病态的。故系统噪声经过转移矩阵P的传播，得到的重建亮温图像误差较大。

根据奇异值分解理论，转移矩阵P的有效奇异值(非零奇异值)个数等于转移矩阵的秩。所以，对于秩亏的转移矩阵，必然存在σmin=0，即转移矩阵为病态的。对于图2中的双L阵，其转移矩阵P的大小为276×188, P的秩rank(P)为161，故双L阵的转移矩阵是秩亏且是病态的。

显然，在所有阵列中，满阵的秩应是最大的[11]，表1讨论了不同大小的满阵所对应的转移矩阵P及其秩的大小。可以看到，在2维镜像综合孔径中，即使是天线数最多的满阵也存在秩亏问题。故可以得出，在镜像综合孔径中所有阵列的转移矩阵均存在秩亏问题，转移矩阵为病态的。

表1 满阵的秩

4 截断奇异值分解

截断奇异值分解是一种正则化方法，在信号降噪[12,13]、特征提取[14]、数据压缩[15]、数据反演[16]、图像加密[17]等领域均有广泛地应用。本文将截断奇异值分解用于镜像综合孔径的亮温重建过程，获取式(3)的稳定近似解。

对于式(3)中的转移矩阵P( V ∈Rm×n)，存在正 交 矩 阵U( U ∈Rm×m)和 正 交 矩 阵V(V ∈Rn×n)，使得矩阵P可以表示成

其中， Λ=diag(σ1,σ2,···,σr)为矩阵P的奇异值组成的对角矩阵，且满足σ1≥σ2≥...≥σr。

由图5可知，矩阵P的奇异值由大到小，逐渐为零。对于无噪声的系统，非零的奇异值才是有效的。而对于含有噪声的系统，等于零的奇异值与部分由噪声引起的较小的奇异值均是无效的，会导致解向量CV与精确解偏差很大。为此，对矩阵P采用截断奇异值分解，截去较小的奇异值，保留较大的奇异值，以减小 cond(P)，降低矩阵P的病态性，提升结果的有效性与稳定性。截去较小的奇异值后，用剩余的奇异值重新构建转移矩阵P为Pr

其中， σk> 0，为截断阈值，小于此阈值的各奇异值均被截断。

因此，利用截断奇异值分解进行亮温重建的步骤为：

(1) 对镜像综合孔径的转移矩阵P进行奇异值分解；

(2) 观察奇异值曲线，根据实际情况，选择合适阈值，截去小于阈值的奇异值及与其相关的左、右奇异向量；

(3) 利用截断后的奇异值及与其相关的左、右奇异向量，构建新的转移矩阵Pr；

(4) 由新的转移矩阵Pr与相关输出向量R求解出余弦可见度向量CV；

(5) 利用求解得到的余弦可见度获得重建亮温。

对上一节中的仿真，采用截断奇异值分解后，得到的成像结果如图6所示。可以看到，此时的成像结果与理想情况下的成像结果接近，背景噪声明显减少，图像轮廓清晰，图像误差ΔT = 17 K，验证了该亮温重建方法的有效性。

5 实验

下面通过实验进一步对截断奇异值分解的亮温重建效果进行验证。

实验系统为镜像综合孔径微波辐射计系统(Mirrored Aperture Synthesis at the V band,MAS-V)[18,19]。MAS-V接收系统工作在V波段51～59 GHz，共7个频点，通过调节本振的频率可以实现不同频点的切换。MAS-V系统共24路接收通道，包括6个四通道射频前端模块、3个八通道中频模块。接收天线阵列可排布为不同的阵列形式：1维线阵、T形阵、U形阵、双L阵等。实验时，系统工作频率设置为51.6 GHz，接收天线单元为矩形喇叭天线。阵列排布与仿真相同，为24单元的双L阵，相邻天线间最小间距为3.5倍波长，实物图如图7(a)所示。带双反射板的MAS-V系统观测电暖器的实验场景如图8所示，反射板与阵列距离为1.75倍波长。此时，系统在两个维度上的空间分辨率分别为0.0184 rad与0.0248 rad[8]。场景目标为电暖器，如图7(b)所示。场景目标与天线阵列距离约为4 m。

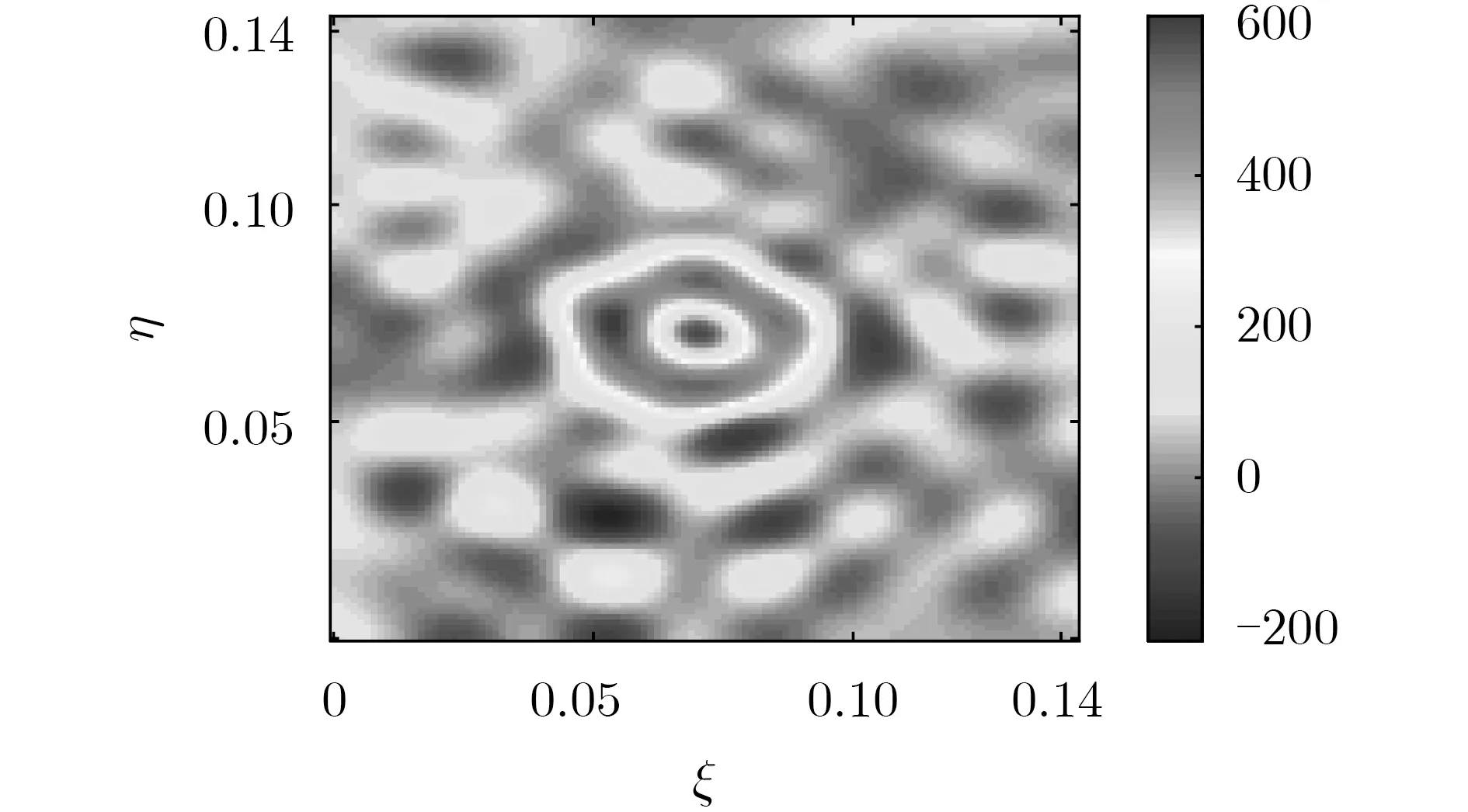
图6 截断奇异值分解后的重建亮温图像

由于实际系统不可避免地存在误差，由式(2)求解的余弦可见度函数存在较大误差，得到的重建亮温图像质量较差，如图9所示。采用截断奇异值分解后得到的重建亮温图像如图10所示，图像质量提升明显，电暖器的轮廓较清晰。由于电暖器中部受金属遮挡，成像结果成环形高亮温，与实物图吻合。实验结果有效验证了截断奇异值分解的有效性。

图7 实物图

图8 实验场景

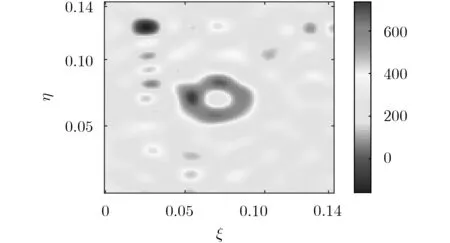
图9 电暖器的重建亮温图像

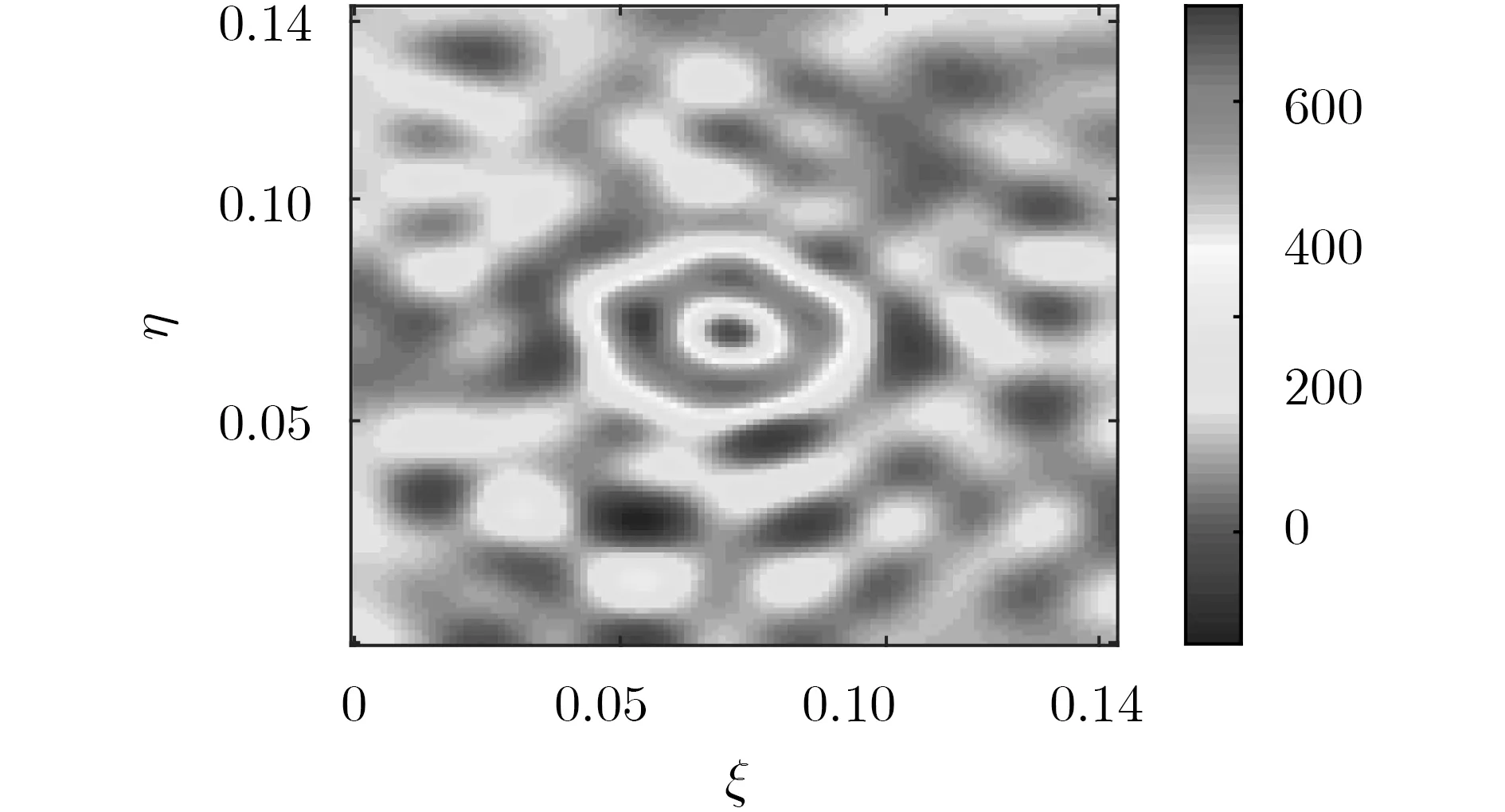
图10 截断奇异值后的电暖器重建亮温图像

6 结论

由于镜像综合孔径转移矩阵的病态性，求解的余弦可见度函数十分不稳定。实际系统的相关输出不可避免地存在误差与噪声，经过转移矩阵的传播扩大，余弦可见度函数存在较大误差，导致最后反演的亮温图像失真。本文给出了一种基于截断奇异值分解的镜像综合孔径亮温重建方法，较好地解决亮温重建中存在的病态问题。并对电暖器目标进行了仿真与实验。从仿真与实验结果可以看出，采用截断奇异值分解后的重建亮温图像背景噪声明显减少，目标轮廓更清晰，并且仿真中的图像误差从103 K减小到17 K。结果表明截断奇异值分解能有效降低噪声，对图像质量的提升起到重要作用。