一种用于工业过程监测的鲁棒迁移字典学习算法

阳春华, 梁慧平, 黄科科*, 李勇刚, 桂卫华

S chool of Automation, Central S outh University, Changsha 410083, China

1.引言

过程监测对工业系统来说是必要的和有意义的，并吸引了工业界和学术界相当多的关注[1-4]。一般来说，过程监测方法分为三类：基于模型的方法、基于知识的方法和数据驱动的方法[5-8]。基于模型的方法使用系统的数学表示，将对系统的物理理解纳入监测方案。基于知识的方法使用图形模型，如Petri 网、多信号流图和贝叶斯网络（BN），用于系统监测和故障排除。这种方法特别适合于耦合系统的预测[9]。数据驱动的监测方法不需要反应机理或过程的机理知识。近年来，通过利用智能传感器、数据分析和深度学习技术的快速进步，数据驱动方法已经被开发出来，以提高诊断的有效性和性能[10]。该领域的进展包括玻尔兹曼机、支持向量机（SVM）、卷积神经网络（CNN）等[11-13]。近年来，数据驱动的方法已经成为复杂工业过程监测的主流。

然而，目前大多数数据驱动的方法均假定历史训练数据和在线监测数据遵循相同的分布[14-16]。事实上，从实际工业过程中收集的数据总是受到许多因素的影响，如多变的操作环境、原材料的变化和生产指标的修改[17]。当基于训练数据学习的模型被应用于实际在线监测时，这些因素常常导致模型失配等问题。这样的问题使其难以实现精确的过程监测。为了解决历史训练数据和在线测试数据遵循不同分布的问题，研究者已经做了很多的工作。Hou等[18]提出了一个用于时变过程监测的增量主成分分析（PCA）在线模型。在这个模型中，当获得一个新的样本时，PCA 模型利用原来的PCA 模型和新的样本进行更新，预测误差平方（SPE）和T2的控制限也被更新。Jiang等[19]提出了一种基于当前数据和历史数据的多模型判别部分最小二乘法（DPLS）来诊断数据。Zhang等[20]建立了一个深度信念网络（DBN），该网络具有很强的泛化能力，可以在线监测焊接状态。为了适应新数据样本的增加，Zeng 等[21]提出了增量局部保存投影（LPP）算法，该算法通过使用拉普拉斯矩阵和原始样本的投影值来更新。然而，这些算法不能应对两个域之间的巨大差异，例如，被监测的工业过程处于一个完全不同的操作环境。Ge和Song[22]提出了在线批处理独立成分分析-主成分分析（ICA-PCA）方法，在该方法中，使用从模型库中选择合适的ICA-PCA 模型来监测新数据。然而，这种方法需要构建多个模型，而且数据的不平衡性会降低监测性能。

字典学习通常学习一个过完备的字典，然后，原始数据可以通过字典和稀疏矩阵进行重构。真实的原始数据通常具有结构冗余的特点。通过字典学习，原始数据被映射到一个较低的维度空间，从而消除了原始数据的结构冗余，同时保留了最简洁的信息。Peng等[23]提出了一种通过LPP计算出一个映射字典的方法，以保留原始数据的几何结构。Chen等[24]提出了一种利用字典正则化从少量目标域数据中学习字典的方法，同时保障这个字典与从源域数据中学习的字典相似。Zhang 等[25]提出了一种方法，在该方法中，为了实现跨域分类，学习了一个公共字典、一个源域字典和一个目标域字典。在Jie等[26]提出的方法中，学习了源域字典和目标域字典之间的若干个子空间字典。Long 等[27]提出了迁移稀疏代码（TSC），该方法引入了图的正则化并减少了分布距离，以实现知识迁移。这些字典学习方法在信号重建、信号降噪、图像识别、图像校正等方面取得了很大的成就，引起了学术界和工业界的高度重视。此外，最近的研究表明，字典学习在过程监测中具有非凡的优势。Huang 等[28]提出了一种核字典学习方法用于实现非线性过程监测，以及一种分布式字典学习方法用于实现高维过程监测。

尽管上述方法在工业系统中表现出卓越的过程监测性能，但它们没有考虑历史数据和在线监测数据的分布差异。迁移学习是不同域间知识迁移的一般框架，近年来得到了广泛的研究，特别是在人工智能、图像识别和计算机视觉界。受字典学习强大的表示能力和迁移学习的跨域知识迁移能力的启发，本文提出了一种鲁棒迁移字典学习（RTDL）方法，用于处理现实工业过程监测的数据分布畸变问题。本方法是联合表示学习和域自适应性迁移学习的一种协同方法。简而言之，历史训练数据和在线测试数据被分别作为迁移学习问题的源域和目标域。对于一个工业系统来说，虽然系统总是在不同的运行环境中运行，会不可避免地导致不同的数据分布，但其内部的基本信息，如机理，往往是相同或相似的。换句话说，工业系统的高维观测数据往往在不同域间有不变的子空间。因此，将源域和目标域映射到一个公共的子空间是可行的，在该子空间中源域和目标域之间的分布差异被消除。之后，在该子空间中进行过程监测。在实际应用中，提出了一种判别性的字典学习方法，从多模态工业数据中提取特征。接下来，提出了最大平均差异（MMD）正则化[29]作为非参数距离度量来表达分布距离，减少了源域数据和目标域数据之间的分布畸变。此外，为了减少模内数据的距离，引入了线性判别分析（LDA）正则化。因此，即使源域和目标域受到不同操作环境的严重影响，本方法也能学习到一个鲁棒的公共字典。因此，该方法能有效地提高过程监测和模态识别的性能。

本文的主要贡献如下。第一，提出了一种RTDL 方法，以减少工业系统多变的运行环境所带来的负面影响。通过减少域间差异，本方法可减少由多变的运行环境引起的过程监测和模态识别的性能下降。第二，给出了关于带约束不可微分字典学习问题的详细优化步骤，可以有效实现RTDL 的求解。第三，通过大量的实验验证了本方法，包括数值仿真实验和实际工业实验。实验结果表明，该方法在精度上优于一些先进的方法。因此，该方法适用于工业系统的过程监测任务。

本文的其余部分组织如下。第2节简要介绍了域自适应迁移学习、字典学习和本文的动机。第3 节提出了RT‐DL 模型并给出了其有效的优化步骤。第4 节进行了广泛的实验，包括数值仿真、连续搅拌釜加热器（CSTH）基准和风机系统实验，以验证RTDL方法的有效性。第5节为结论和总结意见。

2.相关知识

2.1.域自适应迁移

假设有一个拥有大量数据的源域（Xs=[xs1,xs2,...,xns]，其中ns是源域数据Xs的数量）和一个拥有少量数据的目标域（Xt=[xt1,xt2,...,xnt]，其中nt是目标域数据Xt的数量）。这里，源域和目标域是相关的，但不相同。以风机系统为例，将风机系统在冬季的过程数据设为源域，在夏季的过程数据设为目标域。这两个域是相关的，因为每个域的数据均是在相同的机理下从同一个风机系统中采集的。然而，由于外部运行环境的不同，两个季节的观测数据往往具有不同的分布。在数学上，各域的输入特征空间是相同的，但各域的边缘分布和条件分布是不同的，即Xs∊χ、Xt∊χ、Ps(x)≠Pt(x)、Ps(y|x)≠Pt(y|x)。其中Ps和Pt分别代表源域和目标域的概率分布；χ代表数据空间；x代表数据样本；y代表数据x的标签。

为了实现目标域的过程监测，需要消除源域和目标域之间的分布差异，即条件分布差异和边缘分布差异。当源域和目标域的分布畸变消除后，源域数据可以表现出与目标域数据相同的过程信息，因此该方法可以利用丰富的源域数据辅助训练模型，从而达到积极的知识迁移效果。

2.2.字典学习

字典学习的思想是通过学习由一系列原子组成的字典和一个稀疏矩阵来最小化数据重构误差。假设XN=[x1,x2,...,xN]∊Rm×N是一组原始样本，其中xN表示维数为m的第N个样本，R是向量空间，N表示数据量。DK=[d1,d2,...,dK]∊Rm×K是由K个原子组成的字典，其中dK是第K个原子，K是原子数。SN∊RK×N代表稀疏矩阵。字典学习的问题可以表示如下：

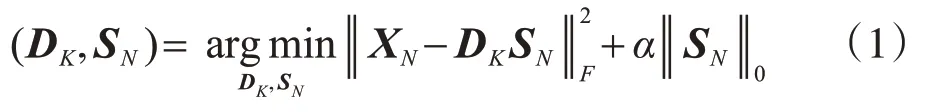
式中，α（α>0）是控制SN稀疏性的参数；‖ ‖•F表示矩阵XN的F范数；‖ ‖•0表示矩阵SN的L0范数。

2.3.本文动机

如前所述，尽管一个工业系统在不同的运行环境下（如不同的地点、时间、天气和人工操作等外部干扰）运行时，会不可避免地导致数据分布的畸变，但基本的内部机理往往是相同或相似的。也就是说，不同域下的工业系统的高维观测数据往往具有不变的子空间。因此，有必要提取不变的知识或子空间，以消除外在干扰，从而进一步提高工业过程监测的性能。为了生动地展示源域数据和目标域数据之间可迁移特征的效果，图1显示了仅受不同环境因素影响而导致不同分布的数据散点图。源域和目标域的边缘分布和条件分布明显不同。传统的数据驱动方法有两种常见的策略。如图1（a）所示，第一种策略是忽略源域数据，只用目标域数据作为输入数据，这样可以满足训练数据的分布与测试数据的分布相同的假设。然而，由于目标域的训练数据非常少，最终的模型很容易出现过拟合。如图1（b）所示，第二种策略是忽略源域和目标域的不同特征。这种策略直接使用大量的历史数据和少量的新数据来进行模型训练任务，因此，最终的模型会混淆域间差异信息和异常信息。此外，该模型很容易被拥有大量样本的源域所支配。相比之下，图1（c）是本文提出的RTDL模型。该方法试图找到一个映射关系函数Φ(·)。通过这个映射关系，原始数据被映射到一个子空间。在这个子空间中，源域的边缘分布和条件分布与目标域的分布相同；也就是说Ps(Φ(x))=Pt(Φ(x))，Ps(y|Φ(x))=Pt(y|Φ(x))，其中Φ(x)是关于x的映射。我们认为如果Φ(·)能克服外在环境的干扰，只保留最简明的内部机理信息，就能将知识从源域迁移到目标域。也就是说，通过在字典学习目标函数中加入MMD 和LDA-like 的正则化，RTDL 方法可以利用丰富的源域数据来辅助训练模型，达到迁移的效果，以提高工业过程监测的效果。

3.方法

在详细讨论该方法之前，这里先引入一个假设。这个假设是合理的，且通常情况下工业系统满足这个假设。

假设：一个复杂的工业过程常常以不同的模态运行，以满足不同的现实需求。在不同的模态下，观察到的变量的特征是不同的。为了清楚地描述不同的观察结果，历史训练数据和在线测试数据分别被看作是源域和目标域。

一般来说，进行多模态数据过程监测有两种方式。第一种方式是单独处理多模态数据，然后单独完成过程监测任务。第二种方式是全局处理多模态数据，然后使用单一模型完成过程监测任务。当在每个单独模态下收集的数据足够时，第一种方式是更好的选择。然而，对于实际的工业过程监测任务来说，目标域的数据总是严重不足，单独的方法容易造成过拟合，因此，最好是全局处理多模态数据。此外，观察到的变量不仅由工业过程的内部机理决定，还受到外在环境（如人工操作、不确定性、参数测量的不连续性、噪声等）的影响。在线测试数据的外在环境与历史训练数据的外在环境不同，所以会出现域畸变。为了获得准确的过程监测结果，一个明智的选择是通过使用域自适应迁移学习的方法来消除无关的外在干扰。

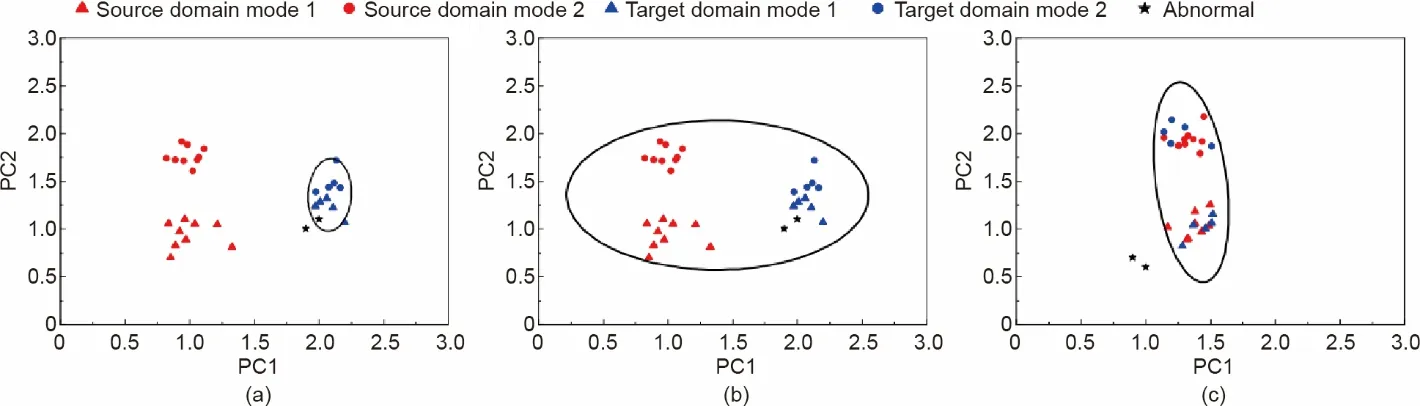
图1.源域数据量大而目标域数据量小的情况。（a）传统策略1：忽略源域，仅利用目标域数据进行模型训练。（b）传统策略2：忽略源域和目标域的特征差异，直接利用所有数据进行模型训练。（c）RTDL模型将源域和目标域的数据进行正则化约束，消除域间差异。该模型是三种模型中最合理的。PC1和PC2表示数据的两个主要成分。

3.1.判别性字典

传统的字典学习已经被广泛地引入过程监测。此外，最近的研究表明，学习判别性字典可以使字典具备模态识别能力[30-33]。因此，对于过程监测任务来说，迫切需要一种判别性的字典学习方法。这里，判别式字典被表示为D=[D1,D2,...,DC]∊Rm×Ck，其中C代表模态的数量；k代表每个模态的原子数量；DC是一个由k个原子组成的子字典，用来代表第C个模态的特征。原始样本矩阵（X）关于字典D的稀疏矩阵为S=[S1,S2,...,SC]∊RCk×(ns+nt)，其中SC=[SsC,StC]；SsC代表第C个模态源域数据的稀疏编码；StC代表第C个模态目标域数据的稀疏编码。为了简单起见，我们将Xi关于字典D的稀疏编码记为Si=是Xi关于子字典DC的编码系数；Xi是由第i个模态样本组成的矩阵（i∊{1,2,...,C}），是X的子矩阵。

为了提高多模态数据的表示能力，应该在字典学习中加入先验约束。第一，数据应该被字典和相应的稀疏矩阵很好地重构，即X≈DS。第二，数据应该被它自己的子字典和子稀疏矩阵很好地表示出来； 即Xi≈第三，由于数据可以由它自己的子字典和子稀疏矩阵很好地表示，因此项应该尽可能地接近于零，公式（1）可以转化为以下形式[31]。

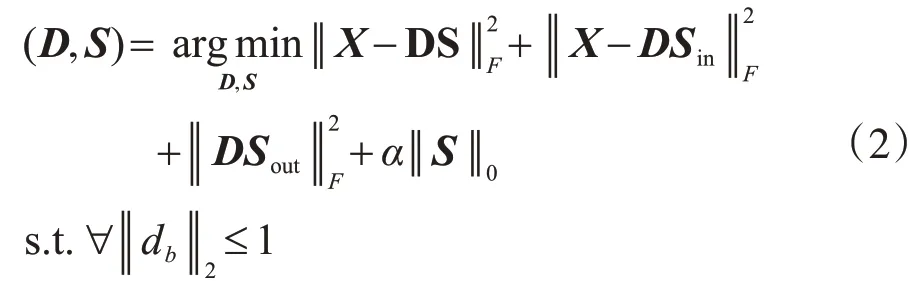
式中，db代表字典D中的第b个原子；Sin和Sout是关于S的表达式，如下所示。

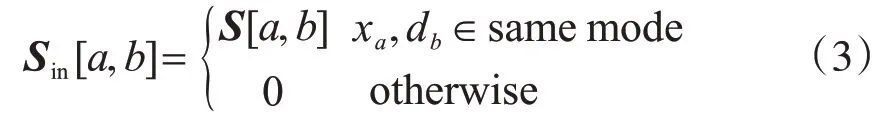
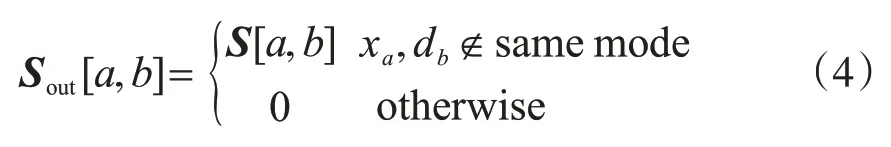
式中，xa是X的第a个样本。

3.2.正则化

由于工业系统的源域和目标域受到不同环境因素的影响，所以数据分布是不同的。为了确保学习到的字典能够捕捉到源域和目标域中潜在的公共机理信息，而不是无关的外在干扰，一个直接的方法是通过最小化一些预定义的度量来减少分布差异。MMD正则化被认为是一种表达域间分布差异的非参数指标[27]，它可以使稀疏矩阵Ssi和Sti的中心接近。在数学上，MMD正则化表示如下。

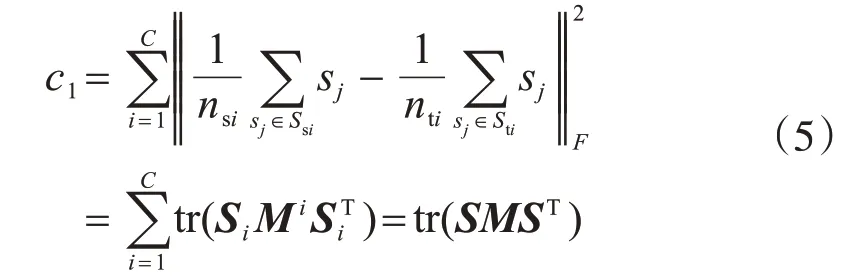
式中，c1代表源域和目标域之间的MMD正则化；nsi和nti分别代表源域和目标域中第i个模态的样本数；sj是稀疏矩阵S中的一个稀疏代码；Mi代表MMD矩阵M的第i个模态部分，可以计算如下。

众所周知，同一模态下的观测数据的分布应该是相同的。然而，由于工作环境的不确定性，同一模态下的数据也表现出一定的差异。为了消除不确定环境的干扰，无论数据来自哪个域，最好使同模态数据的稀疏码彼此更加接近。也就是说，Si=[Ssi,Sti]∀i∊{1,2,...,C}的每一个列向量均应该相互接近。因此，的值应该尽可能小，其中是Si的中心。因此，应该引入以下约束条件。

式中，c2是所有模态的模内距离；I是单位矩阵。LDAlike矩阵H可以通过以下方式得到。

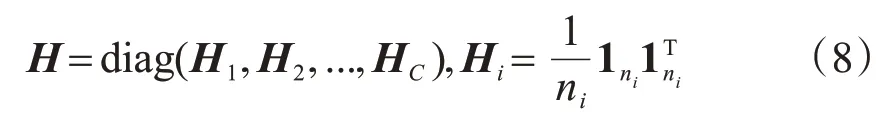
式中，1ni是一个长度为ni及所有元素均等于1的向量；ni是第i个模态在源域和目标域的总数据数。公式（7）的正则化形式上与LDA 正则化相似[34]，所以它被称为LDAlike正则化。

总之，MMD和LDA-like正则化可以被认为是一种渐进的关系。MMD正则化使每个模态的源域中心接近每个模态的目标域中心。作为补充，LDA-like正则化使同一模态的数据相互靠近，以减少模态内的距离。基于这两种正则化的协同作用，我们将公式（2）、（3）和（7）连接起来，形成了本文中所提出的方法，该方法的目标函数可以表示如下。

式中，β1和β2（β1,β2>0）分别是MMD 正则化和LDAlike正则化的超参数，这些超参数可以平衡重建误差和正则化约束之间的权重。由于本方法减少了源域和目标域之间的分布畸变，因此可以达到消除外在环境干扰的效果。

3.3.优化

上述目标函数的优化变量是D和S。由于优化问题不是两个变量的联合凸问题，而是分别凸于D（保持S固定的情况下）和凸于S（保持D固定的情况下），因此引入迭代优化方法来计算D和S的最优值[35]。

3.3.1.更新D

当通过固定S更新字典D时，目标函数可以简化为如下形式：

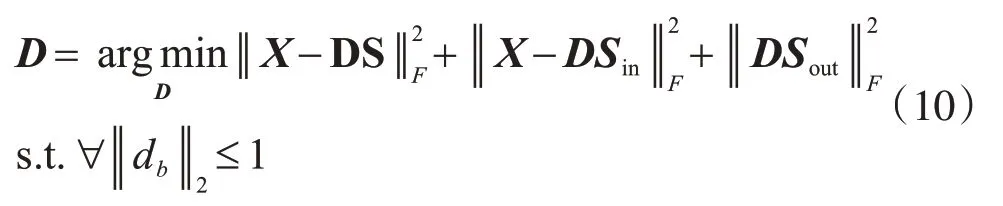
构建了一个新的数据矩阵Xnew=[X,X,O]和一个新的稀疏矩阵Snew=[S,Sin,Sout]，其中O是与矩阵X维度相同的零矩阵，目标函数[公式（10）]变为如下形式：

该目标函数可以通过使用拉格朗日对偶法[35]来有效解决。首先，考虑拉格朗日函数：

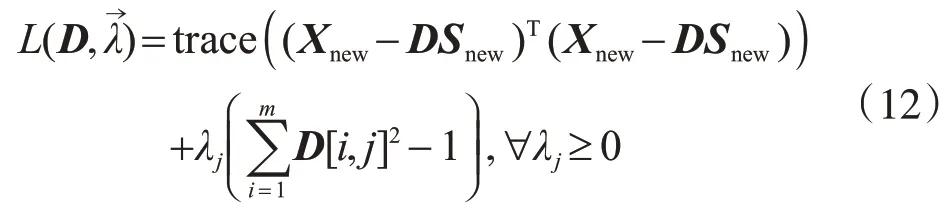
式中，L是拉格朗日函数；是引入的非负参数。

通过最小化拉格朗日函数[公式（12）]得到拉格朗日对偶问题，如下所示。

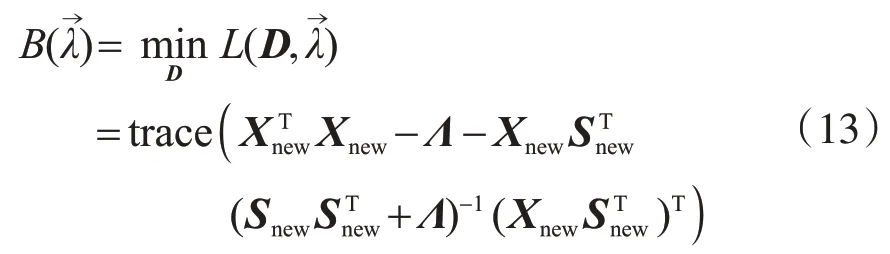
式中，B是拉格朗日对偶公式；Λ是由组成的对角矩阵，拉格朗日对偶问题[公式（13）]可以用牛顿法或共轭梯度法来优化。在最大化B(λ→)后，我们得到最优字典D如下。

3.3.2.更新S

矩阵S将被逐列进行更新。当更新其中一列sj时，目标函数可以表示如下。

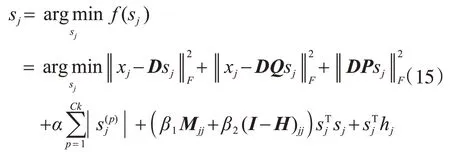
式中，Q、P和hj是目标函数简化过程中的中间变量。Q=(β1Mjj'+β2(I-H)jj')sj'。Q是一个对角线矩阵，元素1只存在于sj所属模态的相应的k个位置上；xj是X中的第j个样本；是sj中的第p个元素。我们通过特征符号搜索算法[27,35]来优化公式（15）。定义g(sj)如下：

式中，g(sj)是公式（15）的可微分部分。为了实现公式（15）中的特征符号搜索算法，引入以下定理。

定理1：定义一个关于x的连续函数为F(x)=G(x)+的最优必要条件为

式中，G(x)是关于向量x的连续可微函数[35-36]；xp是向量x的第p个元素；∇pG(x)是G(x)关于xp的偏导。

证明：我们通过反证法来提供一个简短的证明。假设最优解x中有一个元素xp不符合上述最优必要条件。首先，对于|xp|≠0，∇pG(x)+λsign(xp)≠0，则很明显可知∇pF(x)=∇pG(x)+λsign(xp)≠0。因此，我们可以找到另一个值x*p来代替xp，使F(x*)值更小。这与x为最优解的假设是矛盾的。其次，对于|xp|=0，∇pG(x)>λ，由于G(x)是一个连续可微的函数，我们可以找到一个x*p<0来代替xp， 并 且 满 足G(x*)-G(x)<λx*p。 因 此F(x*)=G(x*)+这也是与假设相矛盾的。对于|xp|=0，∇pG(x)<-λ，可以用同样的方法来证明该假设不成立。综上所述，命题得证。

根据定理1，公式（15）中的必要条件可以描述如下。

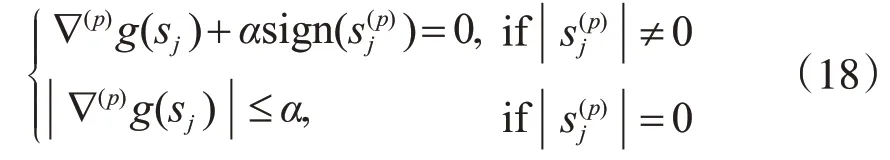
当第一个条件被违反时，因为其符号是已知的，公式（15）中的目标函数是可微的，它成为一个无约束的优化问题（QP）。当第二个条件被违反时，假设∇(p)g(sj)>α，由于∇(p)f(sj)一定大于零，为了最小化f(sj)的值，必须减少。由于从零开始，对其进行的任何无限小的调整均会使其符号为负，因此，我们直接让为−1。那么，f(sj)关于同样是可微的，问题可以简单解决。如果∇(p)g(sj)<-α，可以用同样的方法更新。

据此，稀疏矩阵优化算法的完整过程被总结为算法1。

3.4.在线过程监测

在获得通用字典D后，利用该字典可以进行过程监测和模态识别任务。

3.4.1.过程监测

字典D和正交匹配追求（OMP）算法[37]被用来计算训练集中目标域数据的稀疏表示，训练集中目标域数据的重构残差（RES）可以根据公式（19）得到。

式中，‖ ‖•2代表向量的L2范数；r是样本x的重建误差。

接下来，用核密度估计法（KDE）[38]计算目标域数据的残差分布区间，以检测新的测试数据是否正常。当新的测试数据x来自目标域时，使用同样的OMP 算法得到稀疏代码s；然后使用公式（19）可以得到测试数据的RES。当RES 属于上述分布区间时，它是正常数据，否则，就是故障数据。

3.4.2.模态识别

测试数据被检测为正常数据后，进行模态识别，通过公式（20）来识别数据x。

式中，si是s的子稀疏表示。

综上所述，RTDL的完整流程总结于算法2。

4.验证实验

在本节中，我们在数值仿真、CSTH基准和风机系统上进行了广泛的实验，以证明RTDL方法的有效性和优越性。为了性能的可视化和参数的敏感性分析，在数值仿真中分别引入MMD正则化和LDA-like正则化，以便能够直观地观察样本的分布。对于CSTH基准和风机系统，将提出的方法与一些最先进的方法进行了性能比较。

4.1.性能可视化和参数敏感性分析

4.1.1.数据集

本小节在数值仿真上进行了实验，以验证本文动机并直观地评价性能。数值仿真的数据生成模型如下。

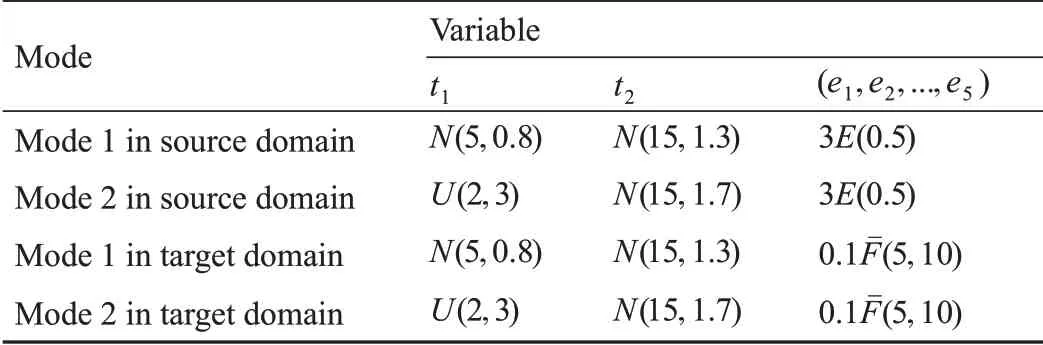
表1 关于仿真数据的细节描述

?

对于训练数据，我们在源域的每个模态收集了100条正常数据，在目标域的每个模态收集了10 条正常数据。对于测试数据，我们在每个模态收集50 条正常数据，在目标域收集300条异常数据。

4.1.2.性能可视化实验

如前文所述，MMD正则化和LDA-like正则化可以从不同角度消除分布畸变。为了验证两者均有消除分布畸变的能力，我们分别引入其中一个，设置另一个正则化参数为零，直观地观察样本的分布。训练数据被利用来学习一个公共的字典。然后通过公共字典和OMP 算法得到源域数据、目标域数据和异常数据的稀疏代码。我们通过PCA将稀疏代码可视化。图2显示了可视化的情况。

图2（a）显示了原始数据的分布。由于环境干扰，域间数据出现了分布畸变，且异常的信息是不明显的。图2（b）、（c）显示，在单独使用其中一个正则化后，分布畸变被部分消除，异常信息通过字典学习后开始显示出来。图2（d）显示，源数据和目标数据完全混合，通过使用两种正则化的方法，异常信息很容易被识别。据此，实验结果验证了本文的动机（第2.3节）。

Algorithm 2.RTDL.Input:Source domain data matrix Xs=[xs1,xs2,...,xns],target domain data matrix Xt=[xt1,xt2,...,xnt],parameters α,β1,and β2 Begin RTDL algorithm Step 1.Initialization Structure data matrix X=[Xs1,Xt1,...,Xsc,Xtc,...,XsC,XtC],MMD matrix M by Eq.(4)and LDA-like matrix H by Eq.(8).D and S are initialized as random values,where Xsc and Xtcrepresent the data sets of Cth mode of the source domain and target domain,respectively Step 2.Off-line training Obtain D and S iteratively To fix S,update D using Eq.(14)To fix D,update S using Algorithm 1 Step 3.Online testing(i)Process monitoring Get the RES limit by D and the OMP and KDE algorithms Conduct process monitoring by comparing the RES statistic and RES limit(ii)Mode classification After the testing data is detected as normal data,conduct mode classification using Eq.(20)End RTDL algorithm

4.1.3.参数敏感性分析实验

参数α是字典学习中一个重要的调整参数，它控制着S的稀疏程度。一般来说，α可以通过观察S的稀疏程度来选择，S的稀疏程度表示矩阵中非零元素所占的比例。如图3所示，当稀疏率（SPR）为20%~50%时，可以得到满意的过程监测结果；据此，对SPR 的参数敏感性分析验证了所提方法的鲁棒性。

接下来，对修改后的β1和β2参数的过程监测性能进行分析。令β1从101变化到105，而β2从10 变化到70。错误报警率（FAR）和故障检测率（FDR）被认为是过程监测的两个评价指标。结果显示在图4 和图5 中。可以看出，当β1和β2改变时，FAR总是低于3%，FDR总是大于80%。尽管β1和β2的变化范围很大，但过程监测的这种性能仍是满意的。当β1和β2的值过小时，学习的字典可以很好地重建训练数据。然而，训练数据中不相关的环境干扰也会被字典学习。当β1和β2的值过大时，目标函数只是减少域之间的分布差异，学习到的字典不能很好地重建过程数据，而且潜在的语义信息，如数据中的机理信息将被丢失。这两种情况均会降低字典捕捉过程数据中常见的潜在信息的能力，导致过程监测的性能不佳。为了给这些超参数选择一个合适的值，可以选择网格搜索这样的优化方法。

4.2.性能比较实验

4.2.1.数据集

由于RTDL在数值仿真中的性能是比较满意的，我们现在考虑其在现实工业场景中的性能。本实验准备了两个数据集。

（1）CSTH。CSTH 过程是一个非线性的真实平台，已被广泛用作评估不同过程监测方法的基准[39]。CSTH的原理如图6 所示。在CSTH 过程中，有两个物理平衡：质量平衡和热平衡。冷水和热水同时流入水槽进行搅拌，同时被蒸汽加热[40]。假设这个过程有两种模态，其中模态状态由液面设置、温度设置和热水阀位置设置决定。详细情况见表2。为了模拟环境干扰，我们在所有观测变量中加入一个指数分布变量，以形成源域，在所有观测变量中加入一个F分布变量，以形成目标域。在观察到的流量变量上施加一个加性故障，以产生异常数据。我们在源域的每个模态收集了100个数据，在目标域的每个模态收集了30 个正常数据，以形成训练数据。测试数据包括每个模态的50个数据和目标域的200个异常数据。

表2 CSTH的传感器电流信号设置参数

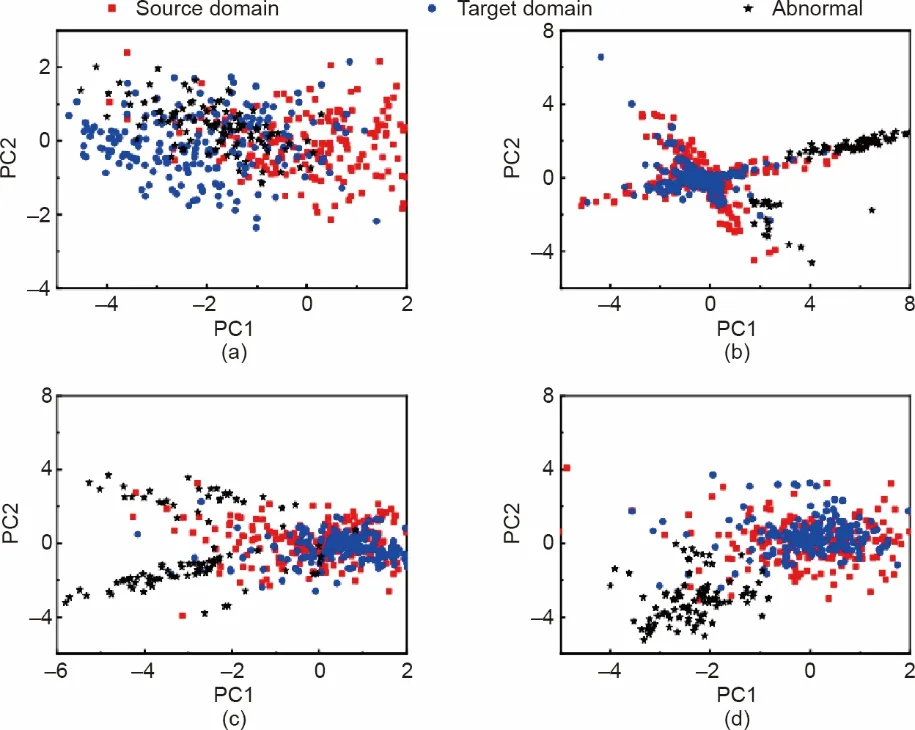
图2.样本分布散点图。（a）原始数据；（b）通过带LDA-like正则化的字典学习得到的稀疏表示；（c）通过带MMD正则化的字典学习得到的稀疏表示；（d）通过同时带LDA-like正则化和MMD正则化的字典学习得到的稀疏表示。

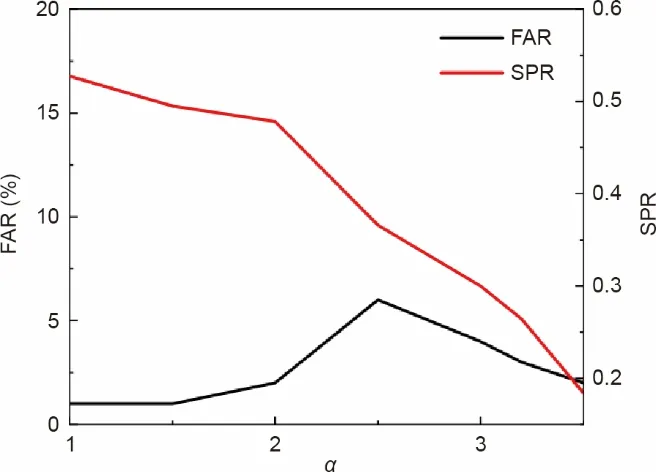
图3.参数α对指标FAR和SPR的灵敏度分析。FAR：错误报警率。

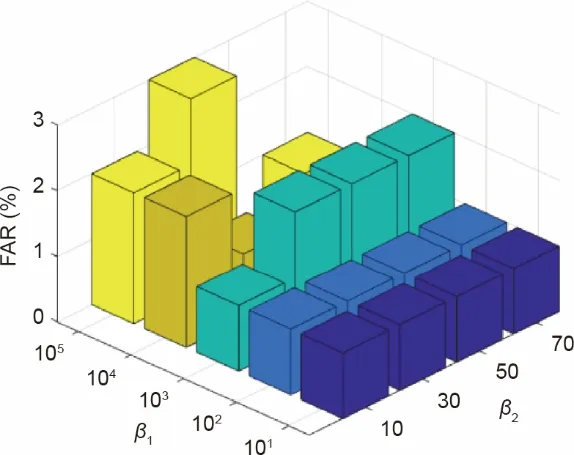
图4.参数β1和β2对指标FAR的灵敏度分析。

图5.参数β1和β2对指标FDR的灵敏度分析。

（2）风机系统。风机系统的数据来自于北京的一家风力发电公司。从2011年1月1日至2011年11月11日，8台风机每分钟采样一次，表3所示的15维数据被用于过程监测和模态识别。每台风机的数据中存在着不同的流形结构，可以认为是风机系统的运行模态。夏季的温度和风力与冬季不同，导致风力发电机组的工作温度和工作功率不同，从而导致数据分布畸变。风力涡轮机系统在不同季节会受到不同的环境干扰。我们假设冬季为源域，而夏季为目标域。详细说明见表4。训练数据由源域中每种模态的350 个正常数据和目标域中每种模态的50 个正常数据组成。每个模态的50个正常数据和目标域的300个异常数据构成测试数据。由于风机系统数据的尺寸差异很大，所有的数据在实验前均进行了标准化处理。

表3 风机系统实验中使用的特征

表4 关于风机系统数据的详细描述

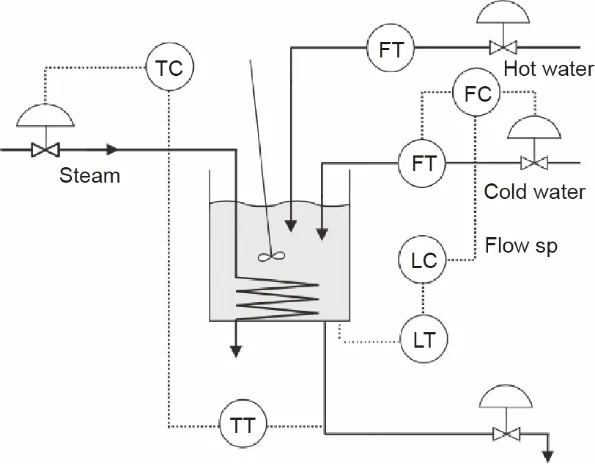
图6.CSTH原理图。TC：温度控制器；FC：流量控制器；LC：液位控制器；TT：温度传感器；FT：流量传感器；LT：液位传感器；sp：设定值。摘自参考文献[40]，经Elsevier许可，©2008。

4.2.2.过程检测的比较实验

为了定量评估RTDL方法，我们使用了另外两种新颖的字典学习方法和一种自适应监测方法进行比较实验。此外，第2.3 节中提到的两种数据处理策略也被用于对比。比较方法包括：label consistent K-singular value decompo‐sition（LC-KSVD）（S+T）、LC-KSVD（T）、Fisher dis‐crimination dictionary learning （FDDL）（S+T）、FDDL（T）、moving window PCA（MWPCA）和RTDL。LC-KS‐VD[41]、FDDL[31]和MWPCA[42]方法是用于过程监测的三种先进的方法。LC-KSVD 和FDDL 同时具有模态识别的能力，而MWPCA是另一种用于过程监测的自适应方法。这里，LC-KSVD（S+T）和FDDL（S+T）分别指LC-KSVD 方法和FDDL 方法，其直接使用所有源域训练数据和目标域训练数据作为输入数据，不考虑域之间的不同特征。LC-KSVD（T）和FDDL（T）分别指LC-KSVD方法和FDDL方法，其只使用目标域训练数据作为输入数据。MWPCA方法直接使用所有源域训练数据和目标域训练数据作为输入数据，不考虑域之间的不同特征。RTDL将源域的训练数据和目标域的训练数据有区别地作为输入数据。为了公平，字典的大小和其他参数被设定为相同。为了比较各模型的性能，我们参考了两个指标：FAR 和FDR。

结果显示在图7和图8中。如图所示，在这两个实际数据集中，本方法在准确性方面均优于对比方法。有一些有趣的结果值得注意，在CSTH中，LC-KSVD（S+T）的FDR接近于LC-KSVD（T）的FDR，但是LC-KSVD（S+T）的FAR明显大于LC-KSVD（T）的FAR。这一结果与我们的观察相吻合，即如果忽略了域的分布畸变，模型可能更容易将域间差异信息与异常信息混淆，导致过程监测结果更差。

4.2.3.模态识别比较实验

本方法可以处理多模态数据，当检测到数据为正常数据时，可以进行模态识别。因此，在本节中，通过与对比方法的比较来评估模态识别的有效性。对比方法的参数设置与过程检测比较实验一样。值得注意的是，MWPCA方法不能完成模态识别任务，所以该方法不用于本实验。为了比较模型的性能，我们参考了两个指标：模态1准确率和模态2准确率。结果显示在表5中。可以看出，本方法在模态识别中的表现优于对比方法的表现，这进一步验证了本方法的有效性。

表5 模态识别结果

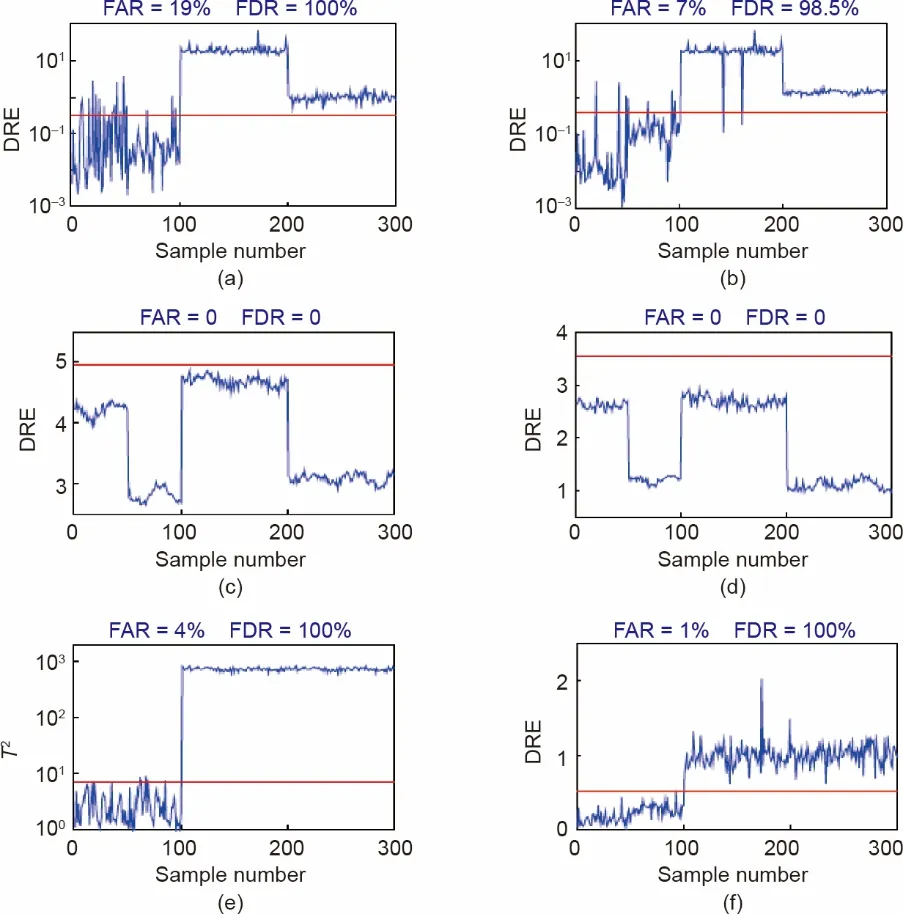
图7.本方法与对比方法在CSTH 上的监测结果。（a）LC-KSVD(S+T)的统计量DRE；（b）LC-KSVD(T)的统计量DRE；（c）FDDL(S+T)的统计量DRE；（d）FDDL(T)的统计量DRE；（e）MWPCA的统计量T2；（f）RTDL的统计量DRE。DRE：字典重构误差。

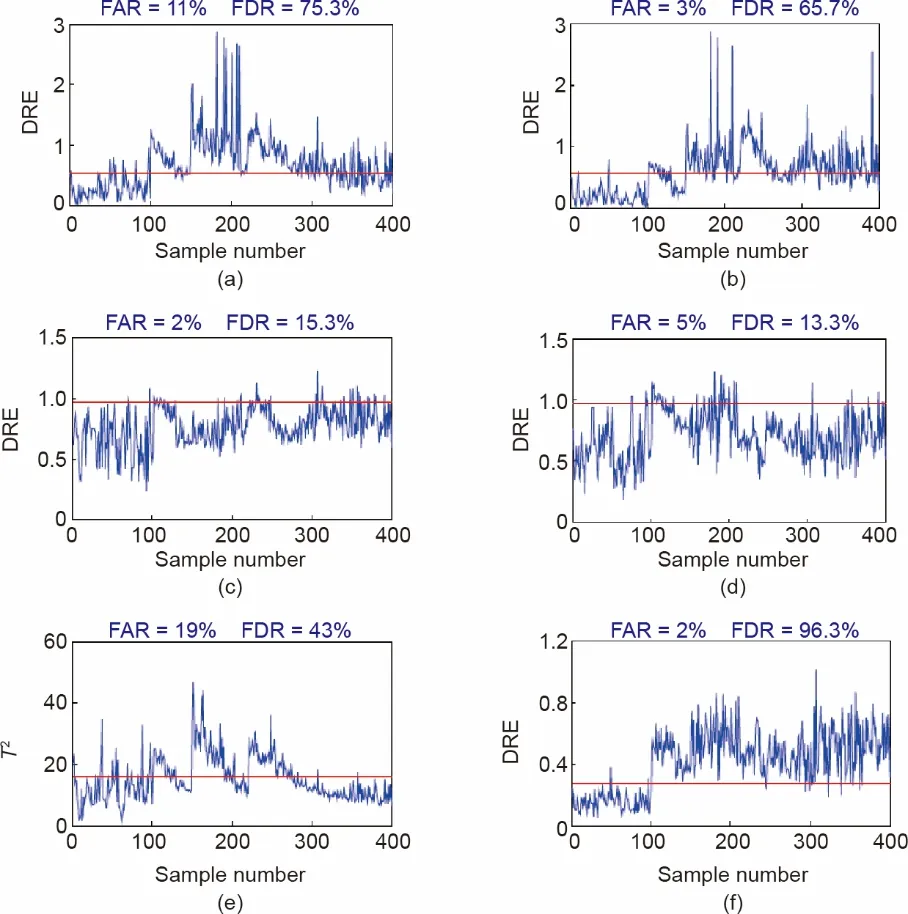
图8.本方法与对比方法在风机系统上的监测结果。（a）LC-KSVD(S+T)的统计量DRE；（b）LC-KSVD(T)的统计量DRE；（c）FDDL(S+T)的统计量DRE；（d）FDDL(T)的统计量DRE；（e）MWPCA的统计量T2；（f）RTDL的统计量DRE。

5.结论

由于工业过程经常受到多变的操作环境的影响，在线监测数据和历史训练数据并不总是遵循相同的分布。因此，基于历史训练数据的过程监测模型不能准确地执行监测在线流数据的任务。为此本文提出了一种RTDL 方法。该方法是一个表示学习和域自适应迁移学习的协同框架。也就是说，首先使用字典学习方法，将原始数据投射到一个子空间，学习一个公共的字典来表示源域数据和目标域数据。在减少子空间中的域间分布距离和模内距离后，消除了环境干扰引起的分布畸变，从而提高了字典表示内部语义信息的能力，如机理信息。通过大量的实验，包括数值仿真、CSTH基准和真实的风机系统，证明了所提方法在域迁移问题上的优越性。因此，可以得出结论，本方法可以将知识从单一源域迁移到单一目标域。由于工业过程通常会遇到多种操作环境，未来的工作将集中在实现从多个源域到多个目标域的知识迁移。

致谢

本研究由国家自然科学基金（61988101）和国家重点研发计划（2018YFB1701100）项目资助。

Compliance with ethics guidelines

Chunhua Yang, Huiping Liang, Keke Huang, Yong‐gang Li,and Weihua Gui declare that they have no conflict of interest or financial conflicts to disclose.