中澳规范混凝土结构受弯承载力对比分析

刘颖,杨明,张春华

(中交第二公路勘察设计研究院有限公司，湖北 武汉 430056)

中国的“一带一路”倡议与澳大利亚(以下简称澳洲)“北部大开发”计划的对接，将推动双方在基础设施建设领域的合作。近年来，以中国交建为代表的中资企业在墨尔本地铁、阿德莱德城市通道工程等方面开展了业务。伴随中国国际工程业务在澳洲的展开，中国标准如何借此机会 “走出去”值得研究。将中国标准推出去，需要科技工作者对澳洲规范开展研究与对比分析。

当前学术上对中澳规范对比研究屈指可数，主要有：熊军辉通过对一算例计算发现，对于轴心受压钢柱澳洲钢结构设计规范比中国钢结构设计规范更为安全；田引安通过中澳公路设计规范对比研究，发现澳洲规范对净空和视距要求高，竖曲线最小半径较大，但其余指标限制值与中国规范比均有不同程度降低。同时，对澳洲规范的研究也较少，主要集中在预应力、消防设计、深梁计算方面。例如，李谦等介绍了澳洲规范AS 3600-2009中预应力结构设计方法及预应力筋材料、预应力损失的计算；邱培芳对澳洲2015版建筑规范中消防性能化设计进行了总体的介绍，分析了该规范的结构特点，对建立适合中国国情的性能化设计规范体系的框架结构提出了几点建议；龚昊骏采用美国、澳洲以及欧洲混凝土设计规范中收录的STM模型设计方法对简支深梁进行了受力分析，发现3种规范计算公式形式基本一致，主要是系数存在不同，计算结果与实际较为接近，而中国规范采用的经验公式计算结果较为保守。

AS 3600-2009《澳洲混凝土结构设计规范》是由澳洲标准委授权BD-002混凝土结构委员会颁布的，是在澳洲、新西兰广泛应用，在斯里兰卡、南非等英联邦国家得到逐步推广的区域性混凝土结构设计标准。然而，当前对应用最广泛的建筑材料——混凝土方面的澳洲规范研究却相当缺乏。为此，该文将以澳洲规范与中国规范中受弯构件的一般规定、设计计算理论和承载力计算等方面的异同点为切入点展开中澳混凝土结构设计规范的对比研究，以期为海外工程设计计算提供借鉴。

1 材料属性的差异

中国规范对混凝土强度等级规定按立方体抗压强度标准值确定，按28 d养护龄期，具有95%保证率的抗压强度值确定。澳洲规范对28 d龄期混凝土强度分两大类进行确定，一般混凝土按AS 1379取规定强度等级，特殊混凝土按AS 1012.9通过试验确定，强度保证率为95%。与欧美规范相同，澳洲规范一般采用圆柱体抗压强度作为混凝土等级划分的依据，标准强度依据混凝土的特征抗压强度划分为8个等级：20、25、32、40、50、65、80、100 MPa。中国规范普遍采用立方体抗压强度作为混凝土强度等级划分依据，包括14个等级，即:C15、C20、C25、C30、C35、C40、C45、C50、C55、C60、C65、C70、C75、C80。常用C30强度等级的混凝土立方体抗压强度为30～35 MPa，其轴心抗压强度标准值为20.1 MPa，设计值为14.3 MPa。澳洲常用32号标准强度等级的混凝土，设计中采用28 d标准养护后设计的特征抗压强度为32 MPa。

中国规范明确400 MPa级钢筋为主力钢筋，倡导使用500 MPa级钢筋，逐步淘汰335 MPa级钢筋。澳洲规范规定了250与500 MPa两种强度等级钢筋，一般使用500 MPa钢筋，根据其延性等级又分为N级钢筋与L级钢筋。对于500 MPa钢筋，澳洲规范采取其屈服强度500 MPa，中国规范采用其轴心抗压或抗拉强度设计值，为435 MPa。

2 设计计算理论

中国规范采用了基于可靠度的概率极限设计理论体系，具体分项系数取值偏重试验所得，结构构件承载力极限状态的设计公式以分项系数表达为：

(1)

式中：γs为作用效应的分项系数；Sk为作用效应的标准值；γR为结构抗力分项系数；Rk为结构抗力标准值;fc,k为混凝土的轴心抗压强度标准值；fy,k为钢筋抗拉强度的标准值；γc为混凝土材料分项系数，取γc=1.4；γs为钢筋材料分项系数，取γs=1.1；As为钢筋截面面积；b,h0分别对应横截面的宽度和有效高度。

澳洲规范采用的是基于概率理论的荷载-抗力系数设计方法，规定设计强度须大于荷载作用效应：

Rd≥Ed

(2)

式中：Rd为设计承载力;Ed为设计荷载作用效应。

其中针对设计承载能力有Rd=φRu，Ru为构件的极限强度。在此澳洲规范采用了承载能力折减系数φ，根据构件所受作用的类型不同，折减系数φ取值如表1所示。

表1 澳州规范折减系数φ的取值

两国规范的设计公式，在形式上虽有差别，实质上都是要求结构的设计承载力大于预期中结构所要承受的荷载效应，以此保障结构的安全性。中国规范中的Rk/γR与澳洲规范中的φRu在概念上是一致的，但中国规范将抗力分项系数γR分解为混凝土材料分项系数γc和钢筋材料分项系数γs，并根据基于概率理论的可靠度方法得到分项系数γc=1.4 和γs=1.1。澳洲规范的结构抗力折减系数φ(0.6～0.8)也是基于概率理论的可靠度方法得到的，只是将结构构件抗力作为一个整体来考虑。

3 受弯设计理论

两国规范中都明确指出混凝土受弯构件弯曲前后符合平截面假定，并且在混凝土应力-应变关系中只考虑混凝土受压。对于除超高性能混凝土等纤维混凝土外的几乎所有混凝土类型这一假定都是正确的，因为常规混凝土结构中和轴以下的混凝土中承担的拉应力很小，可以忽略。两国规范中混凝土受压应力-应变关系如图1所示。

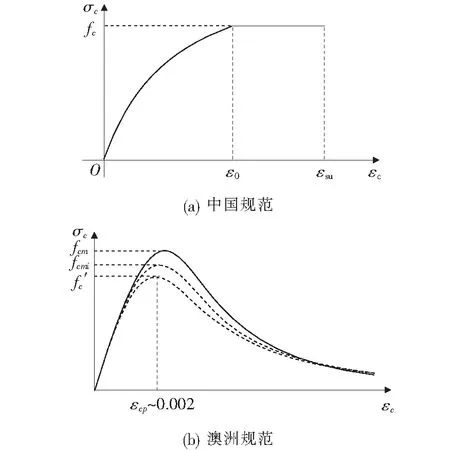
图1 混凝土受压应力-应变曲线

(1) 中国规范[图1(a)]

当εc≤ε0时，

(3)

当ε0<εc≤εcu时,

σc=fc

(4)

(5)

ε0=0.002+0.5(fcu,k-50)×10-5

(6)

εcu=0.003 3-(fcu,k-50)×10-5

(7)

式中:n≤2.0，ε0≥0.002，εcu≤0.003 3。

(2) 澳洲规范[图1(b)]

澳大利亚规范AS 3600 Supplement 1:2014对混凝土的受压应力-应变关系进行了相关规定。根据研究对象的需求，混凝土应力应变曲线中的应力峰值σcp可选取混凝土圆柱体样本抗压强度平均值(fcm)、原位抗压强度平均值(fcmi)或抗压强度特征值(f′c)。

fcm=(1.287 5-0.001 875f′c)f′c

(8)

fcmi=0.9f′c

(9)

混凝土应力-应变关系曲线如下式所示：

(10)

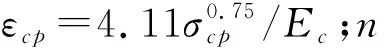
对于混凝土矩形受压区，认为边缘受压纤维最大压应变为0.003。混凝土受压区的等效均布压应力为α2fc′，受压区高度为γkud。α2及γ由下式计算得到：

α2=1.0-0.003f′c(0.67≤α2≤0.85)

(11)

γ=1.05-0.007f′c(0.67≤γ≤0.85)

(12)

为确保构件的延展性，构件在仅考虑弯矩作用下受压截面中性轴到受压边缘的高度与截面有效高度之比(相对受压区高度)kuo不大于0.36(对于仅受到弯矩作用的构件，ku即为kuo)。

中澳两国规范对受弯承载力计算时都采用了基于平截面假定的等效矩形图形计算方法，但假定的混凝土应力-应变关系有所区别，正截面受弯计算等效矩形图以及计算系数略有差别(图2)。

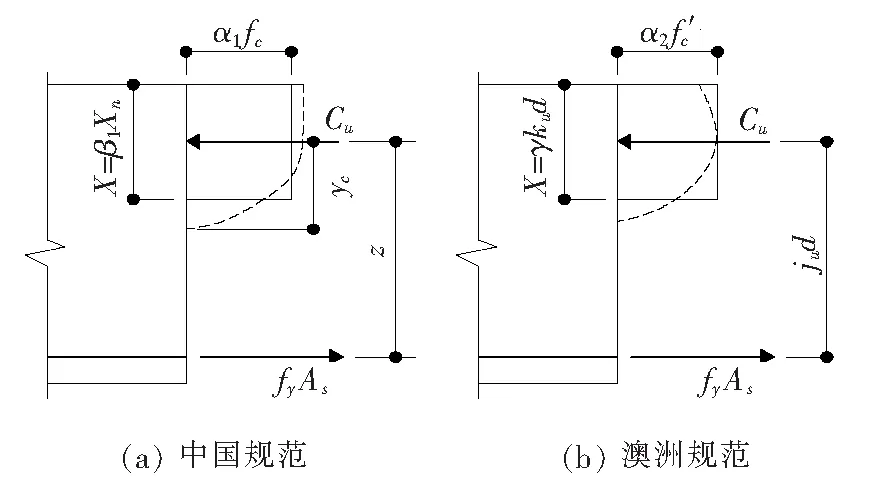
图2 正截面受弯承载力计算简图

4 配筋率的限定

为防止结构发生脆性破坏，中国规范对配筋率有最小限制。对于最小配筋率的计算，有受弯的板或梁结构受拉区混凝土开裂时钢筋刚好屈服，即Mcr=Mcy。

对于钢筋混凝土受弯构件，纵向受拉钢筋最小配筋率为：

(13)

为了防止构件骤然破坏倒塌，澳洲规范对构件的最小抗弯强度进行了规定。要求构件满足最小抗弯强度(Muo)min：

(Muo)min=1.2[Z(f′ct.f+Pe/Ag)+Pee]

(14)

式中：Z为未开裂截面相对于受拉侧边缘的界面模量；f′ct.f为混凝土的抗拉强度特征值；Pe为预应力钢筋的有效应力；Ag为构件截面面积；e为预应力钢筋中心距未开裂截面中性轴的距离。

对于普通钢筋混凝土截面，可通过控制最小受拉钢筋面积来满足构件最小抗弯强度的要求。

Ast≥[αb(D/d)2f′ct.f/fsy]bwd

(15)

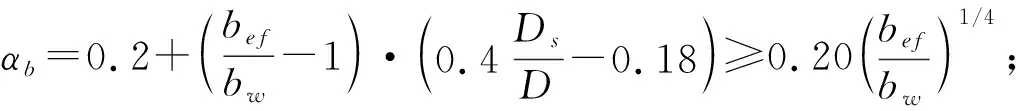
关于最大配筋率的确定，中国规范通过控制混凝土相对受压区高度ξ不超过其相对界限受压区高度ξb来保证结构发生混凝土破坏时钢筋已先屈服。即：

(16)

(17)

澳洲规范同样也对混凝土相对受压区高度(kuo)进行了界定(kuo≤0.36)。

5 极限承载力计算对比

为比较两国规范在计算混凝土构件抗弯极限承载力上的差异，以一个矩形截面梁为例。截面尺寸为250 mm×550 mm，钢筋中心距受拉边缘50 mm(单排钢筋)，C30混凝土，HRB500级钢筋。对应澳洲规范，最为接近的标准混凝土为32号混凝土，其标准强度f′c=32 MPa。

中国规范和澳洲规范计算混凝土梁极限抗弯承载力的公式分别为：

(18)

(19)

式中：h0、d为截面有效高度；b为截面宽度。

在计算过程中，根据两国规范规定，各个参数的取值如表2所示。

表2 抗弯承载力计算相关系数

由表2可见：两国规范抗弯承载力计算的核心思想是一致的：在适筋范围内均是考虑受拉钢筋达到屈服强度，由混凝土受压和受拉钢筋受拉平衡得到混凝土受压区高度，从而进一步计算得到结构的抗弯承载力。两国规范的差异主要体现在材料属性参数，混凝土受压区的等效简化，以及抗弯承载力的折减方法上。

在材料方面，两国规范对混凝土的等级划分有所不同，澳洲规范规定常用混凝度强度等级为32 MPa，与中国规范C30混凝土立方体抗压强度接近，但在设计中中国规范采用混凝土轴心抗压强度设计值，而澳洲规范则是直接采用的抗压强度特征值；对于钢筋强度，结构设计计算中中国规范采用抗压或轴心抗拉强度设计值，而澳洲规范采用钢筋屈服强度。

在混凝土受压区等效简化方面，两国规范均是将混凝土受压区简化成均布受压。混凝土均布压应力转化系数的取值略有不同；此外中国规范未对混凝土等效均布受压区高度进行折减，而澳洲规范提供了等效均布受压区高度系数(γ)。这就导致了在计算混凝土相对受压区高度时，两国计算方法有所差异。

最后在抗弯承载力折减方面，两国采取的方法差异较大。中国规范从材料强度入手，混凝土抗压强度以及钢筋抗拉强度均是采用的设计值，从而对结构的抗弯承载力进行了折减。中国规范混凝土的轴心抗压强度设计值仅有混凝土强度等级的45%～50%。澳洲规范则是直接采用抗弯承载力折减系数从整体上进行折减。

此外，两国规范均规定了最小配筋率的限制，虽计算公式略有不同，但均是出于防止构件的骤然破坏考虑；同时两国规范均通过对混凝土相对受压区高度不超过界限受压区高度的限值规定了最大配筋率，中国规范根据不同强度混凝土搭配不同强度钢筋分别限定了临界相对受压区高度，澳洲规范则是直接规定了相对受压区高度不超过0.36的限值。针对该示例，根据两国规范计算得到的最大及最小配筋率基本一致。根据规范规定，中国和澳洲规范计算的梁的配筋范围分别为0.2%～1.6%和0.164%～1.618%。可见根据两国规范计算所得的配筋率范围非常相近。由于两国混凝土和钢筋的材料分项系数不同，导致配筋率(ρ)对应的混凝土相对受压区高度(ξ)有所区别，具体差异如表3所示。

表3 配筋率及相对受压区高度

在适筋范围内，两国的极限抗弯承载力对比结果如图3所示。

由图3可知，两国规范下梁的配筋率范围相近，且在适筋范围内抗弯承载能力计算结果也相差甚小，其差异在中国规范的±7%以内。在配筋率较小时(<1.2%)，中国规范计算所得抗弯承载力略高于澳洲规范。随着配筋率的增加，两国抗弯承载力差异逐渐减小，配筋率达到1.2%后，澳洲规范计算得到的抗弯承载力高于中国规范。

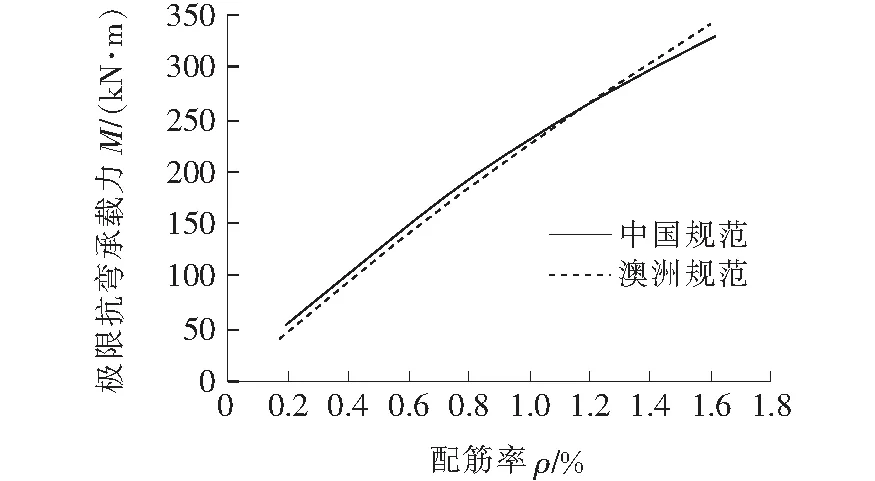
图3 中澳极限抗弯承载力比较结果

6 结语

构件极限承载力计算方面两国规范均采用了基于概率理论的分项系数设计理念，采用的设计公式，在形式上虽有差别，实质上都是要求结构的设计承载力大于预期中结构所要承受的荷载效应，以此来保障结构的安全性。两国规范对于受弯构件正截面承载力的计算公式原理基本相同，但在设计中关于配筋率的限定、材料属性、混凝土受弯构件抗弯承载力计算等方面存在诸多细小差异。

通过中澳两国混凝土结构设计规范构件承载力的具体规定，比较了在受弯构件设计计算中材料属性、设计计算理论、配筋率、极限承载力等几个方面的异同。以期为承接澳洲项目的设计人员提供一定的参考。