基于FLOW-3D的单桩海上风电基础防冲刷数值模拟研究

净晓飞，刘 国，柏延强，贾家喻, 张金凤

(1.中广核研究院有限公司，广州 518034；2. 天津大学 水利仿真与安全国家重点实验室，天津 300072)

结构物附近的海床冲刷在水利工程中十分常见，如桩柱冲刷、管道局部冲刷及水射流冲刷等等。其中，桩柱是近海工程中的常见结构形式，当桩柱放置在海床上时，水流受到桩柱的影响发生局部变化，从而发生冲刷。冲刷会使桩柱的入土深度逐渐减小，导致基础承载力降低，严重影响结构稳定性，因此冲刷防护工作在工程中尤为重要[1]。

许多学者针对不同的海上风电基础型式，开展了广泛的物理模型试验和数值模型的研究，阐明了海上风电基础冲刷的产生机理及希尔兹数、KC数、结构尺寸等因素对冲刷深度及范围的影响[2-11]。近年来，针对泥沙冲刷问题，FLOW-3D软件被广泛应用。与试验相比，数值模拟方法具有经济、便捷等诸多优势，能够较为精确地完成大量重复试验[11]。吉鸿敏[12]等对不同流速下的圆柱绕流流态进行数值模拟，并和模型试验进行了对比验证。史忠强[13]对复合筒型基础的流场进行模拟验证，并对基础周围床面剪切应力进行了研究。黄佳丽[14]等对FLOW-3D模拟冲刷时网格划分以及泥沙参数的选取对于冲刷计算效果的影响进行研究，为冲刷计算和防护设计提供了重要参考。

目前工程中用来预防或者减缓冲刷对桩基础安全影响的方法主要有：将抛石合理配置后抛投于河床上提高基础附近抗冲刷能力[15]；采用土工布、软体排等压实于基础附近保护基础床面[16]；仿生水草治理[17]等。针对不同特点选用不同方法以达到综合治理目的。本文利用三维流体分析软件FLOW-3D分别对海上风电单桩基础无防护下以及抛石和软体排防护下的冲刷进行模拟，分析冲刷深度与冲刷时间关系以及最大冲刷深度，为实际工程中防冲刷措施提供技术支撑。

1 数值模型

数值模拟软件FLOW-3D的基本控制方程包含连续性方程和不可压缩黏性流体运动的Navier-Stokes动量方程。其连续性方程和动量方程中均包含体积和面积分数参数。

连续性方程

(1)

动量方程

(2)

式中：ρ为流体密度；p为流体压强；t为时间；VF为体积分数；x为笛卡尔坐标系中的方向；Ai为i方向上的面积分数；ui为i方向上的速度分量；fi为i方向上的粘滞力加速度；Gi为i方向上的重力加速度。

(3)

式中：τij为液体剪应力；i为作用面；j为作用方向；τij的具体表达式为

(4)

(5)

(6)

(7)

(8)

(9)

式中：μ为动力粘滞系数。

FLOW-3D中有5种湍流模型，分别是零方程模型中的普朗特混合长度模型，一方程模型，标准k-ε模型，RNGk-ε模型，以及大涡模拟LES。其中，RNGk-ε模型通过修正湍动粘度，考虑了平均流动中的旋转及旋流流动情况，可以更好地处理高应变率及流线弯曲程度较大的流动。针对本文拟计算的算例，所建立的数值水池要模拟三维水流与建筑物、床之间的相互作用，比较适合采用该模型来计算。

2 数值模型流速验证

本文采用Kirkgöz和Ardiclioglu[18]明渠流速试验的实测数据对水动力条件参数及边界条件的可靠性进行验证。

数值模型设置基本参数为：水流方向x网格长度为7.0 m，高度方向z网格长度为0.1 m。x向网格数为3 500，为了精确地模拟底部边界层中流速发展情况，对网格z向进行局部加密，从水底至0.02 m划分为20个网格，0.02～0.1 m划分为50个网格，模型总网格数为24.5万。边界条件上，入流侧采用流速边界条件，出流侧采用连续边界条件，底边界采用壁面边界条件，其余边界均采用镜像无通量边界条件。初始水深为0.075 m，计算时间设置为130 s，计算结果输出间隔设置为1 s。

提取数值模型对应位置x=6.5 m处的流速垂向分布，与物理模型数据相比较，结果如图1所示。对比可知，采用FLOW-3D作为数值模拟软件建立冲刷模型，流速剖面与试验值吻合良好，水动力模型满足精度要求。

图1 流速验证

3 冲刷计算结果与分析

3.1 冲刷模型的计算与验证

3.1.1 模型设置

如东二期海上风电项目位于江苏省如东县东部近海海域，风电场处于粉沙质海岸，粒径在0.12 mm附近的粉沙运动特性与工程现场接近，模型所选为天然沙，中值粒径d50=0.121 mm，模型沙与2020年工程区底床泥沙采样物理性质非常接近，都属于粉沙质海岸泥沙，可以体现粉沙在波流作用下的运动特点。

工程所用单桩基础直径5.5 m，水深为11.1 m，平均流速为1.4 m/s。在天津大学水利工程仿真与安全国家重点实验室进行了物理模型试验，采用1:34模型比尺，单向流条件下进行单桩基础周围的冲刷和防冲模型试验。本文针对此试验进行数值模拟并对比。

桩柱直径为0.16 m，沙床厚度为0.4 m，断面平均流速0.24 m/s，水深为0.326 m，水体温度为20°C，动力粘度系数为0.001 Pa·s，试验用沙采用原型沙，粒径为0.12 mm，密度为2 650 kg/m3，重力加速度取981 cm/s2。数值模型的基本参数与试验数据一致，泥沙参数设置具体数据见表1。

表1 模型中泥沙参数设置

由于模型计算过程颇为耗时，因此在不影响正常计算结果的前提下，尽量选取较小的计算区域[19]。冲刷模型中，圆柱距入流边界、出流边界距离均为8D，左右边界和圆柱的距离均为4D。

入流侧采用流速边界条件，出流侧采用压力边界条件，底边界采用壁面边界条件，其余边界采用镜像无通量边界条件。计算时间设置为64 800 s，结果输出设置为600 s 输出一次。在进行纯流作用下的泥沙冲刷模拟过程中，网格的划分对模拟的效率和精度有着重要影响。为了精确地反映圆柱周围沙床的冲刷特征，对模型网格进行嵌套以实现局部加密，将计算域内网格划分为内外两层。外层网格长2.88 m、宽1.28 m、高0.64 m，各项网格尺寸均为0.025 m；内层网格长0.96 m、宽0.96 m、高0.64 m，各项网格尺寸均为0.02 m，网格数共计约18.7万。

FLOW-3D 软件中的泥沙控制方程包括基于梅叶-彼得公式求解平整沙面的推移质输沙率方程和悬移质扩散方程，可较好地预测泥沙的各种状态，模拟出与试验吻合的泥沙运动状态。泥沙模型参数设置对泥沙的悬浮、扩散以及堆积情况有很大影响，其中泥沙临界体积分数Cv反映泥沙悬浮量，泥沙水下休止角φ反映冲刷坑角度，泥沙挟带系数α反映底床泥沙起动浓度，推移质系数β反映泥沙输运量。

由于入流侧速度边界提供的是沿整个水深均一的流速条件，从而造成沙床底部加入流速，将入口处床沙带走，与实际情况不符，为防止此情况发生，在左右侧底边界设置与床面高度相同的实心挡板[20]。挡板上表面粗糙度与沙床表面粗糙度一致为0.3 mm。模型整体网格划分如图2所示。

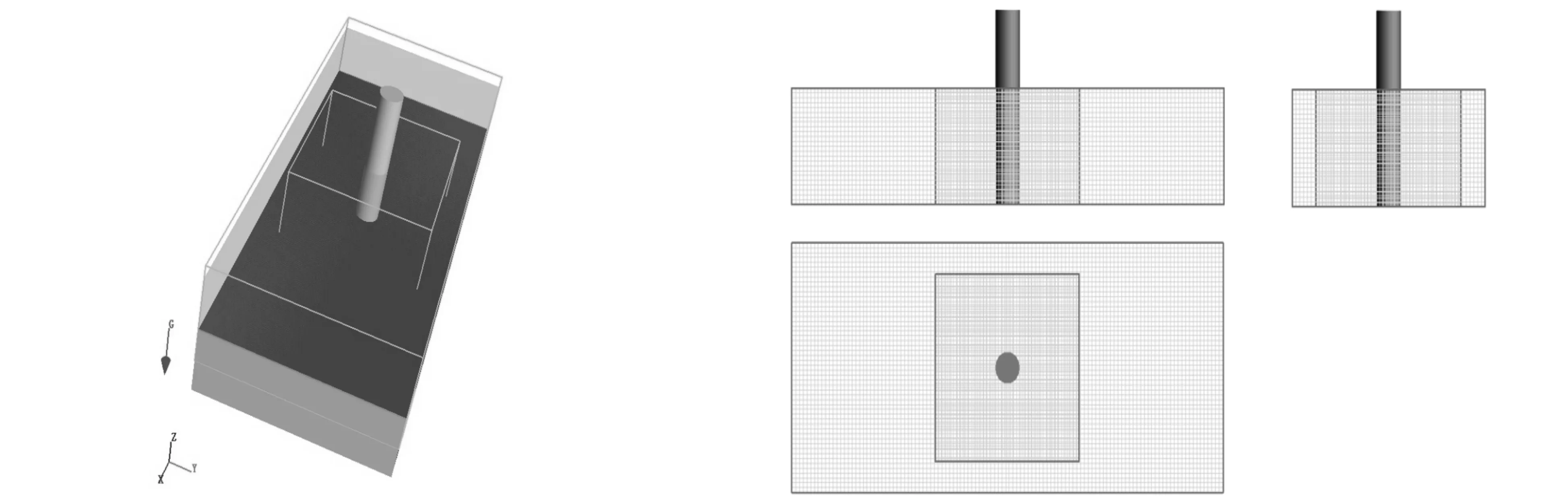
2-a 冲刷模拟模型图 2-b 冲刷模拟网格模型三视图

3.1.2 计算结果与验证

为准确反映冲刷过程中单桩基础周围地形变化、判断冲刷是否平衡及进行试验模型与数值模拟的对比，模型选取8个特征测点进行监测，每个测点距单桩中心15 cm。

对基础周围布置的1、3、5三个测点(图3)进行验证，绘制冲刷深度随时间变化的曲线，可以看出冲刷坑发展过程中模型试验与数值模拟的关系。图4为测点1、3、5冲刷对比图，可见数值模拟结果与试验模型冲刷深度基本吻合，说明本研究中数值计算方法能够较为准确地反应实际冲刷情况，所建模型可以应用于模拟实际工况下的冲刷过程。通过各点冲刷过程曲线可以看出，18 h后冲刷深度值基本不再随时间变化，达到冲刷平衡状态。

图3 测点分布图

4-a 测点 14-b 测点3 4-c 测点5

计算结束后，观察桩柱附近冲刷坑的深度和形状，图5显示了数值计算结果与模型试验照片的对比，图5-a为数值模拟结果，水流从左端流入，可以看出，冲刷坑的形状、大小与图5-b基本相同。越靠近基础冲刷效果较强，冲刷深度较大，形成一个近似于环形的冲刷坑。

5-a 试验模型 5-b 数值模拟

综上所述，模拟最大冲坑深度(9.2 cm)与试验结果(8.4 cm)相差10%左右，产生的原因主要包括：实际情况下泥沙颗粒的运动比较复杂，泥沙起动具有较强的随机性；数学模型计算结果受网格精度影响易产生些许误差。

3.2 抛石防护计算结果

块石防护层对近海结构物抵抗外力侵袭有很好的效果[21]，可用于海上风电基础的冲刷防护，将粒径3.4 mm的砾石防护模型布置于桩柱周围，厚度为2.5倍砾石粒径，铺设范围为3倍桩柱直径D。图6显示了测点1、5、6、8冲刷深度随时间变化规律，发现各测点均在冲刷初始阶段冲刷剧烈，随后冲刷深度随冲刷时间的增加缓慢增加。由于抛石防护仅将沙床表层粉砂替换为粒径较大的砾石，但流场并未改变，故抛石防护下冲刷深度最大位置没有改变，6、8两点冲刷深度最大。

图6 测点1、5、6、8冲刷深度历时曲线图

计算结束后，观察桩柱附近冲刷坑的深度和形状，图7显示了数值计算结果与模型试验的对比，其中图7-a为物理试验结果，图7-b为数值模拟结果。冲刷开始16 h后(冲刷达到平衡状态)，出现明显椭圆形冲刷坑，冲刷坑顺流方向沿桩直径呈对称形态，越靠近桩径部分冲刷越严重，单桩周围2倍桩柱直径D范围内抛石护面发生冲刷。

由图7可见，抛石防护情况下冲刷坑在形态上与无防护条件下冲刷形态相似，但冲刷深度及冲刷范围较小，抛石边缘在水流的作用下也发生移动。由模拟结果可知，模拟最大冲刷坑深度为6.2 cm，冲刷深度减少，在一定程度上对单桩基础周围底床起到了保护作用，但整体已经发生破坏。

7-a 试验模型 7-b 数值模拟

3.3 软体排防护计算结果

复合土工布(即软体排)由上下两层土工布之间缝制成的若干单元体组成，每一单元体内充灌沙子形成肋状结构，沙肋平行于水流方向。由于复合土工布软体排具有很好的柔性，可自动调节整体的形状，能够形成良好的防护线，具有很好的冲刷防护功能。

软体排防护模型(图8)在桩柱周围铺设800 mm×800 mm的软体排，沙肋直径15 mm，相邻6 mm，沙肋内砾石粒径0.12 mm，沙肋平行于水流流向。

图8 软体排示意图

图9显示了软体排角点的冲刷深度随时间变化规律，发现迎水侧角点较背水侧角点冲刷情况严重。迎水侧角点在冲刷开始前3 h仅出现轻微冲刷，随后1 h冲刷效果加剧，之后的8 h缓慢冲刷，冲刷进行12 h后，再次迎来较高强度的冲刷，随后达到平衡状态，冲刷平衡下最大冲刷深度约为2.3 cm。背水侧角点在冲刷开始的10 h仅有轻微冲刷，之后的4 h冲刷加剧，随后冲刷深度略有减小后达到平衡状态，冲刷平衡下最大冲刷深度约为0.8 cm。

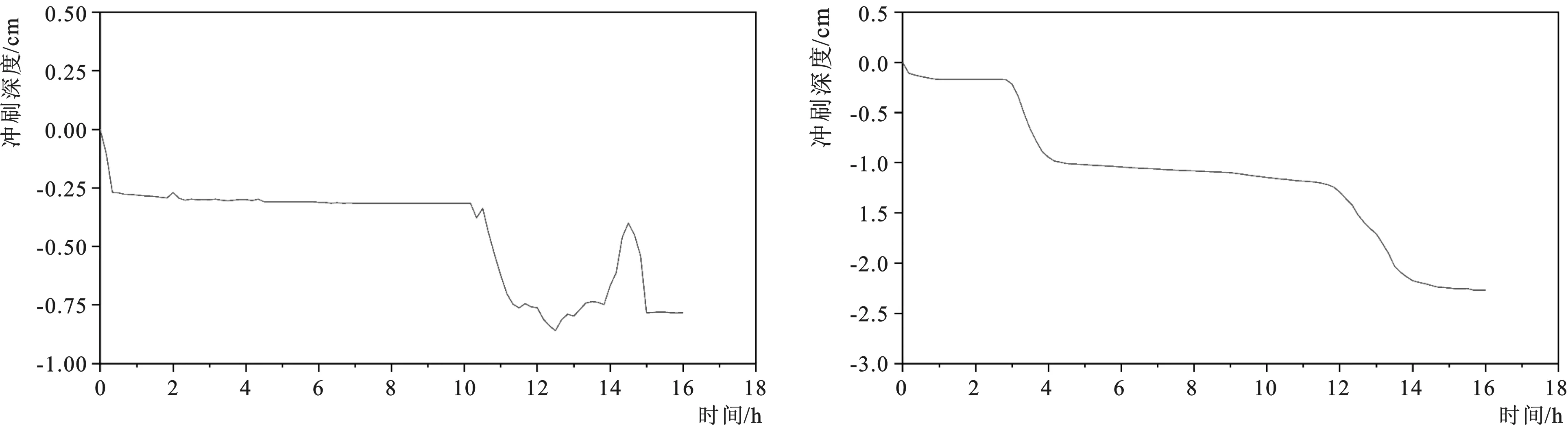
9-a 迎水侧角点 9-b 背水侧角点

计算结束后，观察桩柱附近冲刷坑的深度和形状，在有软体排防护条件下进行冲刷防护试验，冲刷16 h后(冲刷达到平衡状态)，床面沙粒运动覆盖软体排，桩基周围无明显冲刷坑，只有软体排边缘有轻微下陷，最大冲刷坑深度约2.3 cm。

由于模型计算过程颇为耗时，因此在不影响正常计算结果的前提下，在计算域的选择上尽量选取较小的计算区域。

3.4 结果分析

基于数值模拟软件FLOW-3D建立了三维数值水池模型，对冲刷模型试验进行了模拟，并将计算结果与试验结果进行对比验证。

由表2可知所建三维水池模型能够较为准确地模拟物理试验的最大冲刷深度。

表2 最大冲刷深度比较

4 结论

以江苏如东二期海上风电场项目为研究背景，采用FLOW-3D软件对抛石、软体排防护下的海上风电单桩基础冲刷进行模拟，得到了以下结论：

(1)无防护措施时，实验室中单桩基础冲刷由开始至稳定状态历时约18 h，最大冲刷深度达9.2 cm。

(2)设置抛石防护层和软体排后，同样条件下冲刷由开始至稳定状态历时约16 h，最大冲刷深度分别为6.8 cm和2.3 cm，单桩基础附近冲刷坑范围及深度均有所减小，最大冲刷深度约为无防护时的74%和25%。

(3)相比无防护情况，抛石、软体排防护可以增强基础周围海床的抗冲刷性能，使得泥沙不易起动，减少对风电基础的冲刷，使风电基础周围海床更稳定，且沙质海床上单桩基础周围软体排防护效果明显优于抛石防护。