基于新型往返式探空观测的下平流层重力波特征分析*

杨晨义 郭启云 曹晓钟 张 武

YANG Chenyi1 GUO Qiyun2 CAO Xiaozhong2 ZHANG Wu1

1. 兰州大学大气科学学院，半干旱气候变化教育部重点实验室，兰州，730000

2. 中国气象局气象探测中心，北京，100081

1. Key Laboratory for Semi-Arid Climate Change of the Ministry of Education，College of Atmospheric Sciences，Lanzhou University，Lanzhou 730000，China

2. Meteorological Observation Center of China Meteorological Administration，Beijing 100081，China

1 引 言

重力波普遍存在于地球大气中，且具有全球效应。其时、空尺度范围较大，水平波长从十几到几千千米，周期从几分钟到几天。一些研究指出，重力波不仅是稳定大气受到激发的产物，同时也是影响一些中尺度过程发生、发展的因子。在中层大气中，重力波的传播及其动力学效应在决定大气环流的基本性质方面起重要作用。然而，目前对于重力波的发生、发展机制及其对天气过程的反馈机制了解还十分有限，在具体业务中使用重力波进行预报也比较困难。为了了解重力波的形成及各种作用机制并模拟重力波，则需要重力波的活动、分布、变化等气候学特征信息，这些特征可以通过对观测资料进行分析得到。目前，在研究重力波时采用的观测手段主要有：遥感观测（Preusse，et al，2002；McLandress， et al， 2000； Tsuda， et al， 2000；Taylor，et al，1998）、无线电探空观测（卞建春等，2004；吴泓锟等，2019；Bai，et al，2016；Pramitha，et al，2016）、火箭观测（Eckermann，et al，1995；王博等，2017）、飞机观测（Alexander，et al，2000），由于重力波波源的多样性及其在传播过程中背景场垂直结构的复杂性，大气中的重力波在时间和空间上的变化尺度非常大，每一种观测手段只能获取重力波的部分频段特征，而无法获取全貌（Alexander，et al，2010）。

常规高空气象探测作为综合气象观测的重要组成部分（郭启云等，2018a），不仅满足天气、气候分析的需求（郭启云等，2018b），还是地基遥感的相对参考。在下平流层区域内的高空气球探测主要有两类：气象背景要素高空气球和大气成分气球探空。目前，绝大多数气象背景要素高空气球探测在下平流层区域仅仅提供比较可靠的风和温度资料。将高分辨率的垂直探空资料用于分析重力波特征，最初由Kitamura 等（1989）提出并使用，他们利用探空资料计算风速与温度的扰动，并根据所得到的扰动计算出了一系列的重力波参数。卞建春等（2004）和邓少格等（2012）曾详细推导并描述了这一方法的物理意义。这种方法被广泛使用并在以后的各种研究中不断改进，如Zhang 等（2005）曾对武汉附近站点的数据进行过分析，并比较了中、低纬度地区的结果；马兰梦等（2012）曾使用提取出的重力波参数进行了动量通量相速度谱的分析；王丽吉等（2018）使用扩展经验正交函数（EEOF）取代了原有的多项式拟合法，对热带下平流层行星波和重力波扰动进行了分离。此外，吴泓锟等（2019）、白志宣等（2016）也使用上述方法开展了一些研究。

文中所使用的高垂直分辨率往返式探空系统在传统上升探空观测的同时可以利用下降段进行类似“逆上升”的探测进行空间加密，一定程度上解决了传统无线电探空观测的密度问题，并且由于其具有的高垂直分辨率，能够更敏锐地捕捉波动的特征。

2 资料与方法

2.1 往返式探空观测资料

选用的探空观测资料来自新研发的往返探空系统，该系统可以实现“上升段（约1 h）—平漂段（约4 h）—下降段（约1 h）”3 个阶段共计6 h 左右的长时效观测。其下降段可以起到加密观测的作用，且经过验证下降段数据的质量与上升段相近（郭启云等，2018a），平漂段可以弥补平流层—对流层较长时效连续直接观测的空白。且由于夏季平漂距离（放球结束点距放球站距离）约为300 km，文中认为可以视上升段和下降段所测得的结果来自同一个重力波事件，并且由于主要分析的是区域统计特征，即使上升段和下降段所测得的不是同一个重力波事件，但其得出的夏季区域统计结果也具有相近特征。

文中仅选取往返式探空系统的上升段和下降段的数据，由中国东南部的6 个探空站观测试验提供，这6 个站为安庆、长沙、赣州、南昌、宜昌、武汉（图1）。时间跨度为2018 年6 月9 日到2018 年7 月10 日。该数据每日采集两次，分别为07 和19 时（北京时，下同）。数据中所有参数的时间分辨率为2 s。由于气球的上升和下降速度不是均匀不变的，且在下降段气球爆炸后最初的几秒仪器降落速度较快，2 s 内的垂直高度变化过大，所以将所有变量都插值成50 m 间隔。

文中下平流层的下边界由对流层顶确定，上边界由气球的探测高度确定。考虑到6 个站位于较低纬度地区，对流层顶接近18 km 高度，以及Allen等（1995）建议的常用分析高度，文中选取18—25 km的高度进行该地区下平流层的重力波特征分析。数据经过质量控制，剔除了一部分不可信数据，范围内剩余数据为有效数据，各站点上升段和下降段可以使用的数据总量如表1 所示。从表1 可以看到，在廓线总数相近的前提下各站点下降段的数据总量相较于同站点的上升段要少很多，这是因为选取的下平流层高度较高，在该高度范围内下投探空仪多具有很高的速度，垂直分辨率与测量精度都会受到很大影响，这与Gardner 等（1993）的结论较为一致。

2.2 研究方法

以往对重力波的研究多采用小波分析法（覃卫坚等，2010；郝立生等，2006；万明波等，2006），或根据物理量的空间分布特征直观判断波动特征参数和传播方向（许小峰等，2003；龚佃利等，2005；张勇等，2008），进而分析其产生机制及其和天气现象演变的关系。但这些传统分析方法均不能够准确反映大气重力波的实际特征（邓少格等，2012）。文中利用温度廓线和风廓线提取重力波参数进而分析大气重力波实际特征，该方法能够较为准确地描述重力波特征。卞建春等（2004）和邓少格等（2012）曾详细推导并描述了这一方法的物理意义，这里只简要介绍。

图1 探空资料的站点分布（五角星表示）Fig. 1 Distribution of stations （pentagram） where sounding data are used in this study

表1 探空站点信息及测量阶段的数据总量和廓线数Table 1 Information of 6 sounding stations and effective samples in two measurement stages

（1）重力波能量

式中，EK为重力波动能，EP为重力波势能。和表示在选定高度范围内水平风速扰动量的平均值。由于风速垂直分量与水平分量相比要小很多，同时风速垂直分量难以测量，所以式中未考虑垂直方向风速扰动对重力波能量的贡献。N 为Brunt-Vaisala 频率。N 和 ρ都可由探空资料计算得到，g 为重力加速度。

（2）垂直波长式中，m 为重力波的主要垂直波数，通过Yule-Walker最大熵谱分析方法得到归一化温度扰动（）的垂直波数功率谱分布，并选取功率密度最大值的垂直波数作为重力波的主要垂直波数。

（3）固有频率

（4）水平波长

式（5）中， kh为重力波水平波数，可由频散关系（式（6））得到。

（5）传播方向

重力波垂直传播方向可通过水平风速廓线的旋转方向来确定，水平传播方向一般使用拟合椭圆法确定。在北半球，如果水平风速扰动廓线的旋转方向为顺时针方向则重力波能量向上传播，反之则向下传播。

式中， α为从x 轴开始逆时针旋转至椭圆长轴方向的夹角。但其存在180°不确定性，由于纬向风扰动与温度扰动之间存在 π/2的相位差，因此需要利用归一化温度扰动量的垂直梯度与纬向风扰动（ u′）乘积的符号来消除此不确定性（Vincent，et al，2000）。

3 结果分析

重力波根据波源的不同可以分为地形重力波与非地形重力波（以深对流触发为主）。文中所选取的6 个站中赣州、宜昌海拔高度比周边地区高，其余4 个站都处在较为平坦的地带，并且其周围都存在海拔最高不超过1000 m 的山脉。意味着这6 个站所在地区都存在一定的海拔高度差，为触发地形重力波提供了一定条件，但地形高度普遍较低，激发能够传播至平流层的重力波比较困难。由于对流活动也能激发重力波（Hoffmann，et al，2013），这里同样也对产生对流重力波的条件进行了分析。对流是一个比较复杂的物理过程，在发生时往往会伴随着大气层结和风切变的相互作用以及潜热释放等一系列现象，温度层结对对流的限制作用以及风垂直切变对对流的促进作用的相对大小决定了对流是否能够发展起来，这就使得对流激发重力波的机制相较于地形重力波更为复杂。目前，常见的对流源激发重力波机制主要为障碍作用（Lane，et al，2001）、机械振荡（Fovell，et al，1992）和纯热源（Alexander，et al，1995），并且这3 种激发机制相互作用会促进对流重力波的激发，各个机制的相对重要性主要受局地风切变、潜热等因素的影响（Lane，et al，2008）。由于对流源激发重力波的机制相对复杂，且以往的研究表明重力波活动与对流强度的相关性较好，文中选择分析对流产生的条件进而判断对流重力波存在的可能，并且确保波动在因不稳定性破碎或者因多普勒频移作用吸收前被探空观测所捕捉到。因大气热力层结在很大程度上决定了对流活动是否能够形成发展，这里选择浮力频率（N2）表征大气层结稳定度，通过分析浮力频率来判断是否存在通过深对流活动激发重力波的条件。经过计算发现，几乎所有的样本都具有不稳定层结，各站点均有约一半的样本具有能够延伸至下平流层的不稳定层结。相较于比较平坦的地形，研究区域内的对流条件较好，所以认为本研究中所提取的重力波主要为对流性重力波。

为了确保所提取的扰动为重力波，在提取重力波参数前还进行了功率谱分析（图略），发现各次试验得到的波谱都随着频率增大分别存在能量衰减率约为−3 和−5/3 次幂的阶段，对应了重力波能量衰减率和惯性副区能量衰减率，并且在这两阶段中间存在间歇区，与典型的重力波谱特征一致，表明提取的是重力波特征参数，并且该参数是可靠的（斯塔尔，1991；Sun，et al，2015）。

3.1 能量密度

重力波的能量密度大小表征了重力波活动的强弱，对选取的6 个站在试验期间的势能、动能、总能量和动势能比变化特征进行统计（图2）可以看出，各个站因具体试验情况的不同，总成功试验次数不同，但都有50 次左右。

图2 6 个站上升段 （a1—f1） 和下降段 （a2—f2） 下平流层重力波能量密度 （a. 安庆，b. 长沙，c. 赣州，d. 南昌，e. 武汉，f. 宜昌）Fig. 2 Energy density of gravity wave in the lower stratosphere in the ascending （a1—f1） and downcast （a2—f2）sections of 6 stations （a. Anqing，b. Changsha，c. Ganzhou，d. Nanchang，e. Wuhan，f. Yichang）

续图2 Fig. 2 Continued

图2 中的三条浅蓝线分别代表动能、势能和总能量，橙红线代表能量的比值。各站上升段所测得的3 种能量变化相对较为平稳，动能分布在0.4—1.2 J/m3，平均值约为1.0 J/m3；势能分布在0.03—0.5 J/m3，平均值约为0.2 J/m3。因动能比势能大得多，使得总能量曲线与动能曲线趋势相近，只是量值略大，动势能比为2—6，但也有个别试验比值在2 以下或8 以上，说明该地区重力波以惯性重力波而非纯重力波为主。下降段测出的重力波能量波动情况与上升段相近，但更为平稳，量值略小于上升段。动能分布在0.2—1 J/m3，平均值约为0.5 J/m3，势能分布在0.02—0.4 J/m3，平均值约为0.2 J/m3，动势能比在5 附近变化。该区域不同站的能量密度特征及变化的差异较小，可能是所选取的站较为接近造成的（经纬度差异均不足5°）。比较两阶段结果发现，下降段所提取的能量整体小于上升段，这可能是下降段垂直分辨率相对上升段较低，因而漏掉了一些小尺度的重力波。后文分析垂直和水平波长时同样会考虑该因素的影响。文中6 个站结果都与以往研究（白志宣等，2016）中宜昌站结果接近，说明本研究提取的重力波能量密度参数是合理的。

3.2 垂直波长

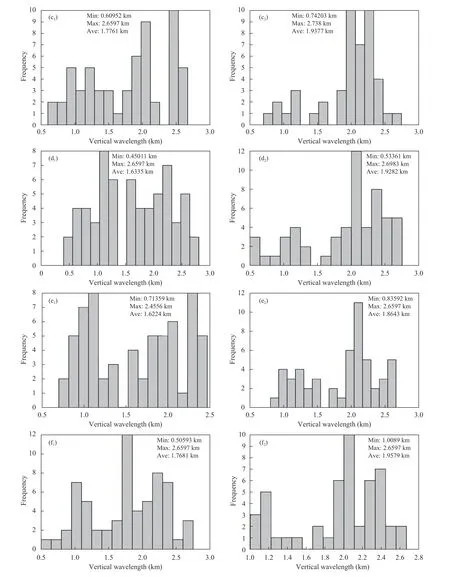
利用Yule-Walker 最大熵谱分析方法得到归一化温度扰动（）的垂直波数功率谱分布，并选取功率密度最大值的垂直波数作为重力波的主要垂直波数（m），从而得出下平流层重力波垂直波长。从6 个站重力波垂直波长频数分布以及最大（小）值和平均值（图3）可以看出，所有站的垂直波长最小值为0.20 km、最大值为 2.73 km，90%的样本分布在1.0—2.5 km，50%的样本分布在2.0—2.5 km，平均波长为1.8 km 左右。从整体来看，各站垂直波长的分布范围以及平均值没有明显差异，下降段所测得的垂直波长各值均略大于上升段。这一结果与3.1 节提出的推测相符，即下降段垂直分辨率相对较低，致使漏掉一些小尺度的重力波。结果还显示，重力波垂直波长的频数分布以1.5 km 为界有两个峰值，分别位于1 和2 km 处。

3.3 固有频率

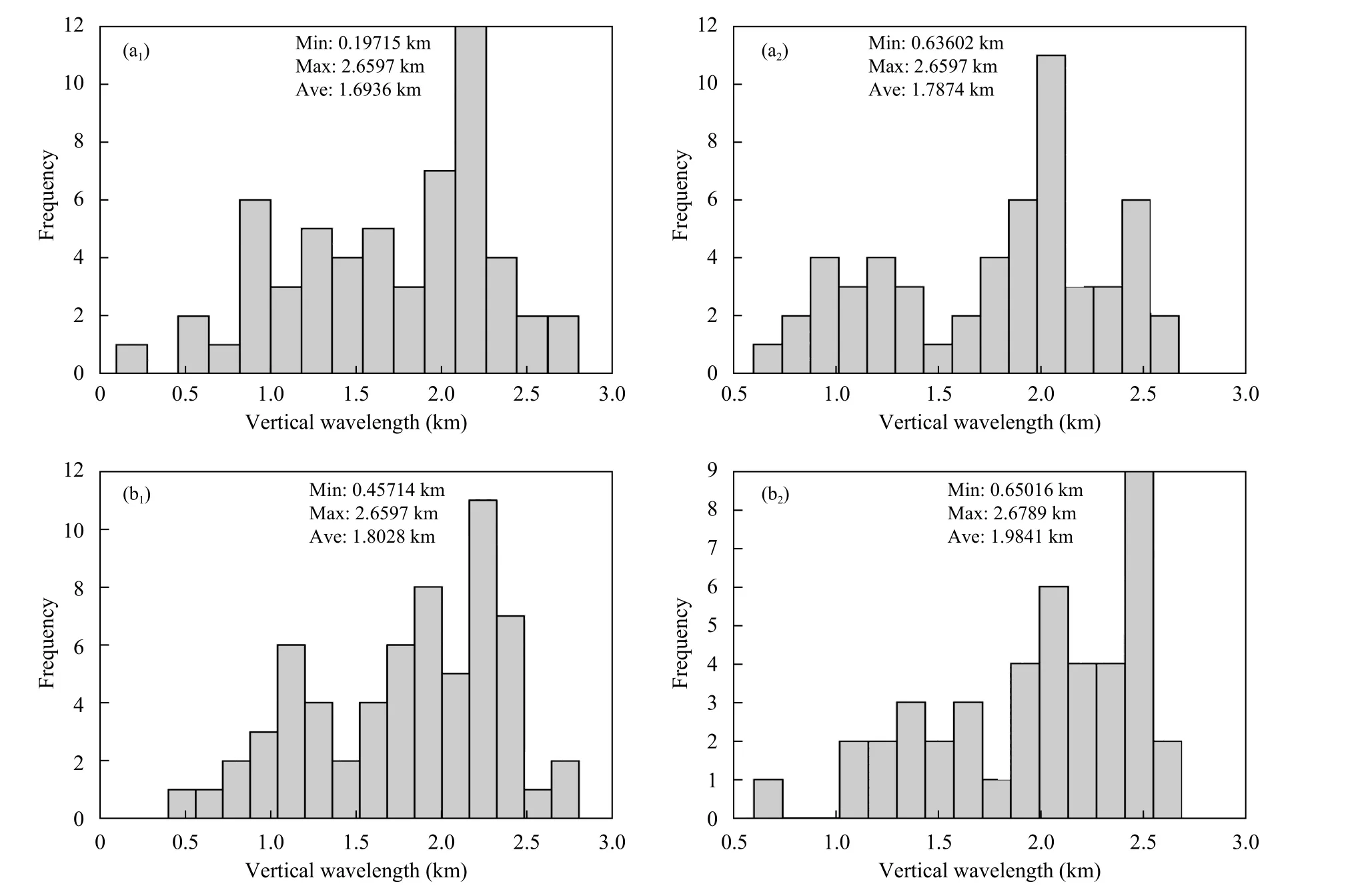
图3 6 个站上升段 （a1—f1） 和下降段 （a2—f2） 下平流层重力波垂直波长频数分布（a. 安庆，b. 长沙，c. 赣州，d. 南昌，e. 武汉，f. 宜昌）Fig. 3 Vertical wavelength frequency distribution of gravity wave in the lower stratosphere in the ascending （a1—f1） and downcast （a2—f2） sections of 6 stations （a. Anqing，b. Changsha，c. Ganzhou，d. Nanchang，e. Wuhan，f. Yichang）

续图3 Fig. 3 Continued

上述结果表明，滤波前、后固有频率的分布变化比较明显，因此计算前应进行必要的滤波处理才能够获得更为准确的固有频率；上升与下降段结果同样存在一定差异但较小。

3.4 水平波长

从6 个站上升和下降段测得的下平流层重力波水平波长频数分布（图6）可以看到，下平流层水平波长在40—1500 km 内均有分布，集中分布在200—800 km，平均值约为550 km。水平波长与垂直波长比约为250∶1，表明平流层重力波在垂直方向的夹角极小，主要在水平方向传播，这也是惯性重力波能够传播到距离波源极远地方的原因，与北京（卞建春等，2004）、四川（吴泓锟等，2019）、华北地区（Chen，et al，2019）的结果相似，但平均值略有不同，且各站之间差异较小。说明尽管在夏季一般存在约为300 km 的平漂距离，下降段数据也能起到对重力波事件的加密观测作用。

图4 滤波前6 个站上升段 （a1—f1） 和下降段 （a2—f2） 下平流层重力波固有频率频数分布（a. 安庆，b. 长沙，c. 赣州，d. 南昌，e. 武汉，f. 宜昌）Fig. 4 Natural frequency distribution of gravity wave in the lower stratosphere （before filtering） in the ascending （a1—f1）and downcast （a2—f2） sections of 6 stations （a. Anqing，b. Changsha，c. Ganzhou，d. Nanchang，e. Wuhan，f. Yichang）

续图4 Fig. 4 Continued

图5 滤波后6 个站上升段 （a1—f1） 和下降段 （a2—f2） 下平流层重力波固有频率频数分布（a. 安庆，b. 长沙，c. 赣州，d. 南昌，e. 武汉，f. 宜昌）Fig. 5 Natural frequency distribution of gravity wave in the lower stratosphere （after filtering） in the ascending （a1—f1） and downcast （a2—f2） sections of 6 stations （a. Anqing，b. Changsha，c. Ganzhou，d. Nanchang，e. Wuhan，f. Yichang）

续图5 Fig. 5 Continued

3.5 传播方向

重力波垂直传播方向一般可通过水平风速廓线的旋转方向来确定，分别分析各站的水平风速廓线旋转方向发现，2018 年6 月9 日到2018 年7 月10 日，6 个站下平流层重力波能量垂直向上传播的概率均大于 90%，且各站结果之间无显著差异。说明下平流层重力波在垂直方向上主要是向上传播，与之前的一些研究（卞建春等，2004; Zhang et al，2007，2010）结果一致。

图6 6 个站上升段 （a1—f1） 和下降段 （a2—f2） 下平流层重力波水平波长频数分布（a. 安庆，b. 长沙，c. 赣州，d. 南昌，e. 武汉，f. 宜昌）Fig. 6 Horizontal wavelength frequency distribution of gravity wave in the lower stratosphere in the ascending （a1—f1） and downcast （a2—f2） sections of 6 stations （a. Anqing，b. Changsha，c. Ganzhou，d. Nanchang，e. Wuhan，f. Yichang）

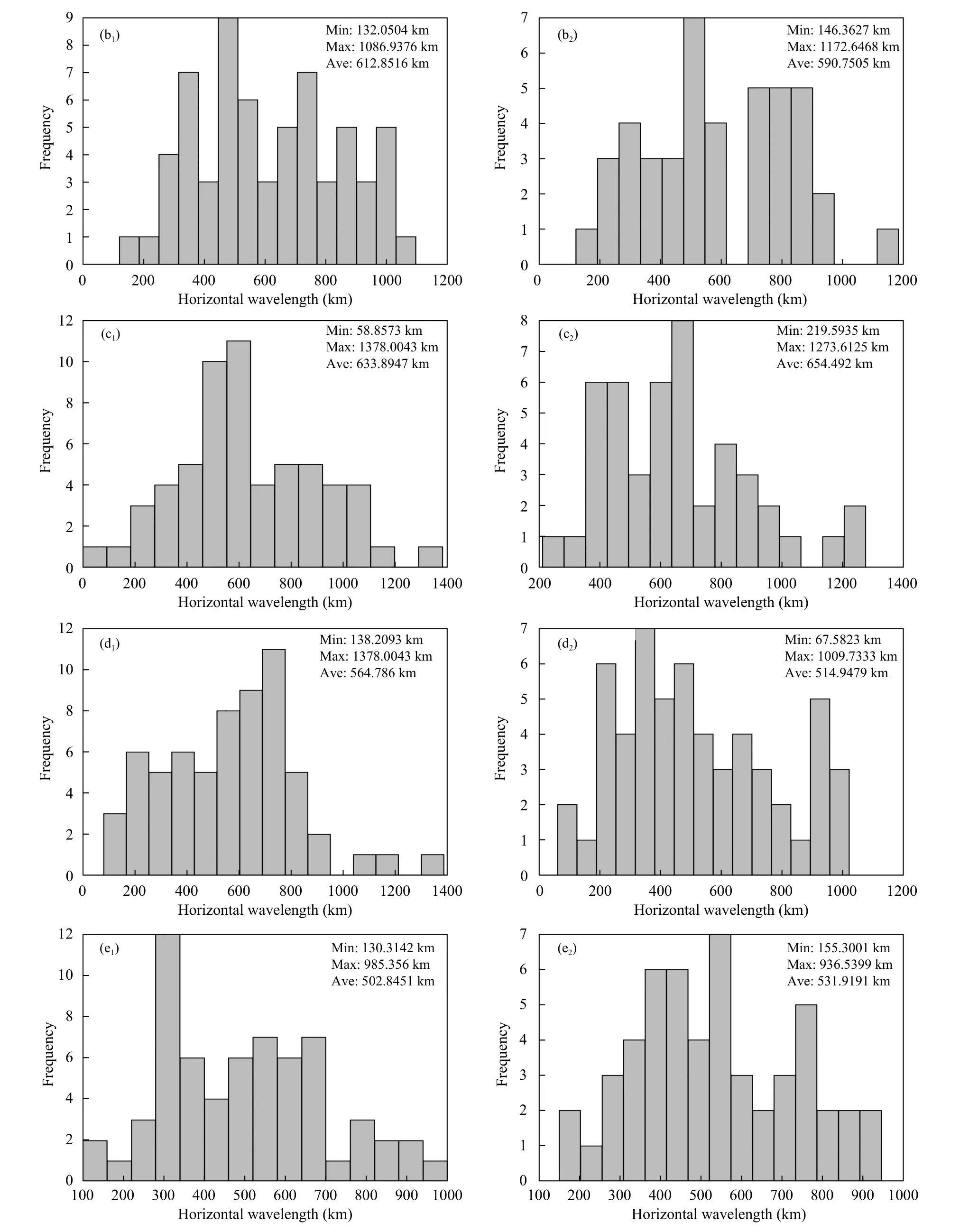
续图6 Fig. 6 Continued

图7 6 个站上升段 （a1—f1） 和下降段 （a2—f2） 下平流层重力波传播方向频数分布（a. 安庆，b. 长沙，c. 赣州，d. 南昌，e. 武汉，f. 宜昌）Fig. 7 Frequency distribution of gravity wave propagation directions in the lower stratosphere in the ascending （a1—f1） and downcast （a2—f2） sections of 6 stations （a. Anqing，b. Changsha，c. Ganzhou，d. Nanchang，e. Wuhan，f. Yichang）

续图7 Fig. 7 Continued

续图7 Fig. 7 Continued

图7 为6 个站下平流层重力波水平传播方向频数分布，扇形的方向表示水平传播方向，扇形的大小表示出现在这个方向范围内的频数，扇形越大表示在这个方向范围内重力波传播的频率越高。从图中可以看出，与其他参数不同，两阶段所测得的水平传播方向特征差异较大，考虑到经过平漂过程后测量位置改变，气球与重力波的相对位置也有改变，这一结果是比较合理的。大部分站的上升段和下降段结果均存在比较明显的主要传播方向，但主要传播方向特征并不一致，以西北向传播最多，其次是北向传播。

4 结论与讨论

利 用2018 年6 月9 日 到2018 年7 月10 日 安庆、长沙、赣州、南昌、宜昌、武汉6 个站的往返式探空系统试验数据，提取重力波能量密度、固有频率、波长以及传播方向等参数，统计了试验地区6—7 月的重力波特征，比较了各站之间以及重力波上升与下降段的差异。主要结论如下：

（1）该区域内下平流层重力波在日尺度上变化明显，并且重力波动能的量值远大于势能，动势能比为2—6，总能量的曲线受重力波动能影响较大。不同站的能量密度特征及变化差异较小，上升段与下降段的差异也较小。

（2）该区域内下平流层重力波垂直波长与水平波长的比值很小，说明平流层重力波以水平传播为主，在垂直方向上的夹角极小，使得平流层重力波能够传播到相对较远的地方。同时说明尽管存在夏季一般约为300 km 的平漂距离，但下降段数据也能起到对重力波事件的加密观测作用，且无论是垂直波长还是水平波长，下降段结果均略大于上升段。

（3）滤波前后固有频率的分布变化比较明显，滤波后结果有向大值方向移动的特征，滤波前固有频率主要分布在1.2 —2 f，平均值为1.7 f；滤波后固有频率的最小值仍为1.2 f 左右，但最大值明显增大，较大值分布频数也明显增多，大部分分布在1.2—4 f，平均值也增大至2.1 f 左右。

（4）与其他参数不同，两阶段所测得的水平传播方向特征差异较大。大部分站上升段和下降段结果均存在比较明显的主要传播方向，但主要传播方向特征并不一致，以西北向传播最多，其次是北向传播。

因主要着眼于重力波的区域统计特征，所以文中将上升段和下降段的结果视为等效并进行了比较分析，但实际上这两阶段的结果存在一些差异，这在后续的工作中需要重点关注：（1）因平漂段的存在，上升段和下降段所处位置发生了改变，因夏季平漂距离（放球结束点距放球站距离）约为300 km，认为可以考虑将上升段和下降段所测得的结果视为同一个重力波事件，并且认为两阶段结果应具有相近特征，除水平传播方向以外的其余参数的结果都比较支持这一假定。但冬季平漂距离相对较远，这时上升段和下降段的结果是否能近似认为源自于同一重力波事件仍有待讨论。（2）分析中发现能量和垂直波长的下降段结果存在相对于上升段结果的整体偏移（偏大或偏小），在分析两阶段数据的差异时认为这可能是因为下降段速度明显偏大，其垂直分辨率偏低，因此相对于上升段会漏掉一些小尺度的重力波，从而影响到能量和垂直波长的统计特征，这一差异较小，但今后在进行其他方向的研究时可能不能忽略，如何在保证上升段高时间分辨率的同时消除这种差异需要进一步讨论。