四种定量降水预报客观订正方法对比研究*
苏 翔 袁慧玲 朱跃建
SU Xiang1,2 YUAN Huiling3 ZHU Yuejian4
1. 江苏省气象台,南京,210008
2. 中国气象局交通气象重点开放实验室,南京,210009
3. 南京大学大气科学学院/中尺度灾害性天气教育部重点实验室,南京,210023
4. 美国国家环境预报中心/环境模拟中心,马里兰,20740
1. Jiangsu Meteorological Observatory,Nanjing 210008,China
2. Key Laboratory of Transportation Meteorology,China Meteorological Administration,Nanjing 210009,China
3. Key Laboratory of Mesoscale Severe Weather Ministry of Education/School of Atmospheric Sciences,Nanjing University,Nanjing 210023,China
4. NCEP/Environmental Modeling Center,Maryland 20740,USA
1 引 言
定量降水预报是最重要的气象预报业务之一(宗志平等,2012;毕宝贵等,2016)。提升定量降水预报质量,对于防灾减灾、工农业生产和公众生活等方面具有重要意义。数值模式是定量降水预报的基础,然而由于初值和模式本身的不确定性,模式定量降水预报存在一定的误差。
对数值模式直接输出的定量降水预报产品进行客观订正是提升定量降水预报质量的有效手段。美国国家环境预报中心(NCEP)在业务上使用频率匹配法(FMM)对全球模式降水预报产品进行客观订正,显著减小了模式定量降水预报的系统偏差(Zhu,et al,2015),该方法在中国进行了一定的推广和应用(李俊等,2014,2015;周迪等,2015;徐姝等,2018a)。袁慧玲等于2013 年从NCEP 引进频率匹配法开发了欧洲中期天气预报中心(ECMWF)确定性降水预报频率订正产品(栾菲,2017),并于2015 年在国家气象中心实现业务运行(代刊等,2016)。江苏省气象台苏翔基于频率匹配法开发了用于订正中国GRAPES 全球预报系统(GFS)确定性降水预报的业务产品,并于2018 年在中国气象局数值预报中心实现业务运行。吴启树等(2017)基于频率匹配法的思路,将频率偏差(Frequency Bias,简称FB)最优改为TS 评分最优,发展了最优TS 评分(OTS)算法,显著改进了ECMWF、日本气象厅(JMA)、NCEP 和T639 模式定量降水预报的TS 评分。此外,由于集合预报产品相比于确定性预报产品可以提供更加丰富的预报不确定性信息,在降水预报中也发挥了越来越重要的作用(Zhu,et al,2002;Buizza,2008;杜钧等,2014)。国家气象中心基于集合预报开发了集合多统计量融合技术(FUSE),对不同降水量级分别参考特定的集合分位数(例如集合最大值、90%集合分位数、75%集合分位数、中位数、10%集合分位数等)进行订正(陈博宇等,2015,2016;徐姝等,2018b)。若将集合多统计量融合技术方法中固定的集合分位数改为根据TS 评分最优滑动建模得到的集合百分位,则转变为更加灵活的最优百分位(OP)技术(代刊等,2018)。最优百分位技术于2015 年在国家气象中心投入业务应用,2015 年夏季24 h 预报时效的暴雨主客观预报评分结果显示,最优百分位法的TS 评分已略超过预报员的预报结果(代刊等,2016)。概率匹配(PM)结合了集合成员的量级和集合平均的空间分布进行模式定量降水预报订正,无需历史训练数据,常用于中小尺度降水集合预报(Chien,et al,2004;Clark,et al,2009;Gallus,2010;Berenguer,et al,2012;Surcel,et al,2014;陈博宇等,2015)。其他定量降水预报客观订正方法还包括分位值映射法(Voisin,et al,2010)、相似 法(Hamill,et al,2006)、多模式集成(李芳,2012;智协飞等,2013)等,具体可参考代刊等(2018)的综述文章,这里不再赘述。
文中重点研究上述的频率匹配、最优TS 评分、最优百分位、概率匹配这4 种常见的定量降水预报客观订正方法,主要目的有以下3 点:(1)厘清上述4 种订正方法的基本概念。目前中国部分科研和业务工作者在使用上述定量降水预报客观订正方法时,由于概念上缺乏清晰的认识以及翻译文献的不准确,出现了将名称相近的方法混淆的情况。例如标注“频率匹配法”的名称但实际使用的是“概率匹配”订正,或是不清楚“集合多统计量融合技术”法和“最优百分位”法的区别;(2)通过理想模型和个例订正加深对不同订正方法的直观理解。TS 评分等传统检验指标包含的信息量有限,预报员难以根据评分大小对不同客观订正方法产生直观的理解。通过理想模型研究原始预报雨区在不同位移和干湿偏差情况下频率匹配和最优TS 评分订正方法的表现,并对4 种不同方法进行个例订正展示,有助于预报员直观地理解上述方法的基本特性,并将其合理应用于主观分析中;(3)检验评估上述4 种定量降水预报订正方法的总体性能。对比不同定量降水预报客观订正方法在全年、不同季节、不同预报时效和不同降水量级下的表现,研究集合预报信息的引入是否有助于预报性能的提升,检验不同预报订正产品在风险决策中的经济价值(Zhu,et al,2002),为气象业务工作提供科学参考。
2 资料和方法
2.1 资 料
气象实况资料为2017 年10 月1 日—2019 年12 月31 日中国2411 个气象站的逐日降水观测(08—08 时,北京时)。数值预报资料为ECMWF 确定性预报资料和集合预报资料,分辨率分别为0.125°和0.5°,其中集合预报包含50 个扰动成员。选取起报时间12 时(世界时),预报时效36—228 h(1.5—9.5 d),间隔24 h,并采用双线性插值将预报插值到2411 个气象站点上。
2.2 检验方法
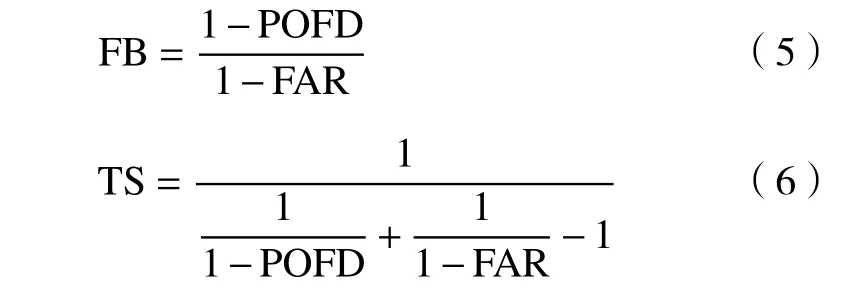
选取2019 年全年为检验期,检验4 个标准降水等级(小雨(0.1 mm/d)、中雨(10 mm/d)、大雨(25 mm/d)、暴雨(50 mm/d))的TS 评分、频率偏差(FB)、漏报率(POFD)、虚警率(FAR),计算方法如下(Jolliffe,et al,2003)

式中,h 为预报和实况同时达到降水等级的样本比例,m 为实况达到降水等级但预报未达到的样本比例,f 为预报达到降水等级但实况未达到的样本比例。
由式(1)—(4)可推知TS 评分、频率偏差、漏报率和虚警率之间存在如下关系
在研究不同季节的预报性能时进一步引入性能图(Performance Diagram)(Roebber,2009;Guan,et al,2017)将不同定量降水预报客观订正方法的TS 评分、频率偏差、虚警率和漏报率在一张图上综合展示,并标注样本基础观测覆盖率(Base Rate,简称BR)。
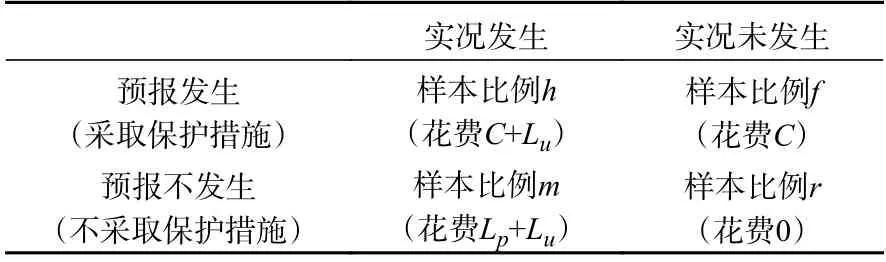
表1 花费和损失的预报与观测二元事件联立表Table 1 Contingency table of costs and losses depending on dichotomous forecasts and observed events
经济价值模型(Zhu,et al,2002)常用来分析不同定量降水预报客观订正方法在风险决策中的表现情况。如表1 所示,假定降水事件发生时:若采取保护措施,花费为 C,但灾害仍会产生不可避免的经济损失为 Lu;若未采取保护措施,造成的额外经济损失为 Lp,总损失为 Lu+Lp。记降水事件的观测频率为s, s=h+m,则完美预报的平均经济损失为

若按预报降水事件是否发生来决策是否采取保护措施,产生的平均经济损失为
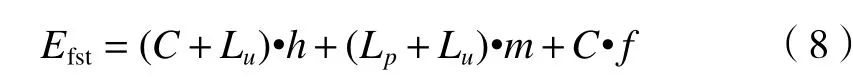
若不参考预报信息,总是采取或总不采取保护措施的平均经济损失分别为
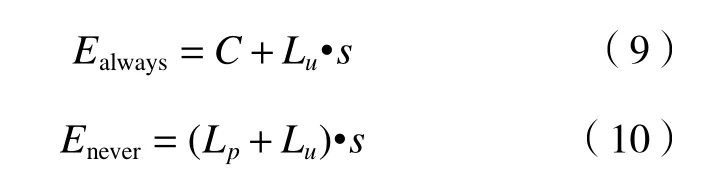
记花费/损失为 α=C/Lp,选取式(9)和(10)中较小的平均经济损失作为参考值
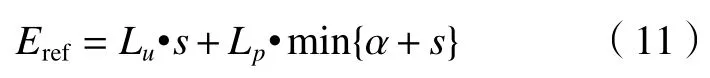
通过式(7)、(8)、(11)可计算通过预报进行决策在减少经济损失方面产生的技巧,即经济价值评分
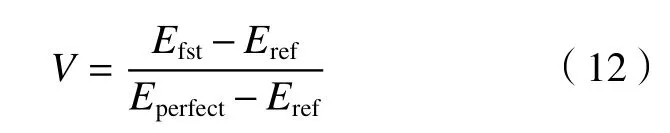
对于特定的预报,经济价值(V)是 α的函数。V 越大代表预报对决策的贡献越大,V>0 代表预报信息对决策减少经济损失有正效果,V<0 代表预报信息对决策减少经济损失有负效果,V=0 代表无效果。
2.3 训练取样方法
针对不同预报时效分别订正,采用长度为61 d的组合对称滑动窗口进行训练样本取样,即距离预报日最近可用的30 d 和上一年同期及其之后的30 d组合而成的滑动对称训练样本。以订正2019 年8 月22 日20 时(北京时)起报的84 h 预报为例,预报的降水时段为2019 年8 月25 日08 时—8 月26 日08 时,选取2019 年7 月24 日—8 月22 日(30 d)和2018 年8 月26 日—9 月25 日(31 d)共61 d 的历史实况和对应的84 h 预报样本进行训练。
此外,还测试了持续滑动窗口取样方法和历史对称窗口取样方法。持续滑动窗口选取距离预报日最近可用的61 d 的滑动训练样本,优点是能够适应模式由于升级更新产生的系统偏差的变化,缺点在于季节更替时前期样本的季节代表性较差。历史对称窗口选取上一年同期及前后各30 d 组成的61 d 的滑动对称训练样本,优点是季节代表性较好,缺点是无法及时适应模式由于升级更新产生的系统偏差的变化。
从理论上讲,组合对称滑动窗口取样方法结合了持续滑动窗口和历史对称窗口的优点。测试结果表明,3 种取样方法和不同窗口长度对检验结果的影响不大。因此,以下选取窗口长度为61 d 组合对称滑动窗口取样方案应用于频率匹配、最优TS评分和最优百分位订正方法中(概率匹配订正不需要训练样本)。
2.4 频率匹配法
频率匹配法使用训练期内的确定性预报和对应的实况资料建立原始预报和预报订正值之间的一一映射关系,目的是消除不同降水等级上的频率偏差,使得预报与观测雨区的总面积保持一致。使用组合对称滑动窗口取样代替Zhu 等(2015)中的卡尔曼滤波算法,并将对订正系数插值改为对预报订正值直接插值,具体算法是:首先,统计一组降水阈值 t1,t2,···,tN对应的预报累积频率 p1,p2,···,pN和观测 累 积 频 率 q1,q2,···,qN,通 过 坐 标(p1,t1),(p2,t2),···,(pN,tN)构建预报累积频率曲线;其次,通过插值计算累积频率 q1,q2,···,qN在预报累积频率曲线上对应的降水阈值g1,g2,···,gN;然后,通过坐标(g1,t1),(g2,t2),···,(gN,tN)构建原始预报值和预报订正值对应的订正曲线;最后,对于任意的原始预报值,可通过线性插值计算其在订正曲线上对应的预报订正值。选取N=10 个 降 水 阈 值 t1,t2,···,tN分 别 为0.1、1、5、10、25、35、50、75、100 和150 mm/d,与 吴 启 树 等(2017)的最优TS 评分方法保持一致。设定订正的上、下界分别为250 和0.1 mm/d,分别用于防止极端降水外插导致过度订正和小雨消空。当原始预报大于订正上界时,保留原值不订正;当订正后的预报小于订正下界时,设为0 降水。
2.5 最优TS 评分法
最优TS 评分法与频率匹配法有相似之处,也使用训练期内的确定性预报和对应的实况资料建立原始预报和预报订正值的对应关系,但目的是通过对雨区面积进行缩放使得不同降水等级上的TS 评分最大。参考吴启树等(2017)的最优TS 评分算法
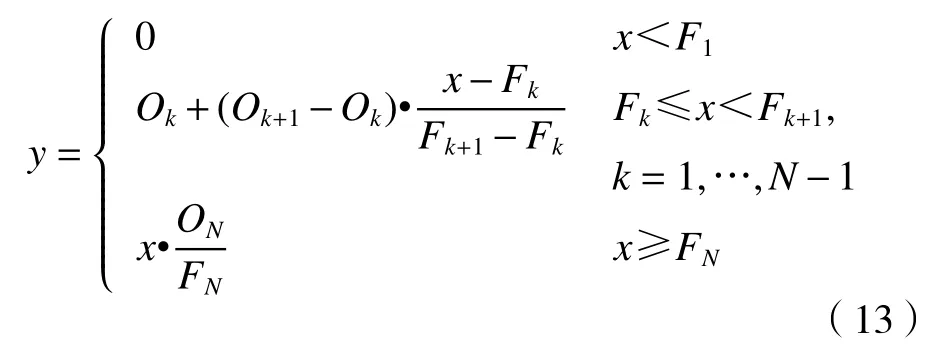
式中,x 为原始降水预报值,y 为降水预报订正值,Ok为第k 等级降水阈值(分别取0.1、1、5、10、25、35、50、75、100、150 mm/d), Fk为原始预报订正到Ok时,该降水等级对应的原始预报降水值。此外,吴启树等(2017)还将35 mm/d 以上降水的订正系数限制在0.8 到1.6 范围内以避免由于高值降水样本偏少导致的订正系数不稳定问题。
2.6 最优百分位法
最优百分位法使用训练期内的集合预报和对应的实况资料,在不同等级降水上寻找TS 评分最大的集合分位数(代刊等,2018)。这里选取的降水等级阈值 tk与2.4 节中的10 个降水阈值相同。对每个 tk,计算训练期内所有样本不同集合百分位0%,2%,4%,···,98%,100%的总体TS 评分,找到评分最优的集合百分位 Xk,然后按照 tk从大到小的顺序依次进行判断:若原始集合预报的 Xk百分位值PXk≥tk, 则订正值为 PXk, 否则对下一个 tk进行判断;若所有判断都不满足,则订正值为0。
2.7 概率匹配法
概率匹配法(陈博宇等,2015)将集合成员的量级和集合平均的空间分布相结合,将实时的集合预报数据直接处理成单一预报订正产品,订正过程不包含历史观测信息。假定预报区域内包含N 个格点(或站点),集合成员数为M,概率匹配算法具体如下:首先,计算区域内N 个格点(或站点)的集合平均,并对集合平均进行排序;其次,对区域内N 个格点(或站点)共N×M 个集合成员进行排序,再划分长度为M 的N 个模块;然后,计算每个模块的平均值,并按模块序号替换相同序号的集合平均值,生成概率匹配订正场。
3 理想模型与个例订正
3.1 理想模型
为了研究不同干湿偏差和雨区位移偏差情形下,频率匹配和最优TS 评分法对原始预报(RAW)的订正效果,构建了如图1 所示的理想模型,其中实况观测雨区是半径为1 的单位圆,预报雨区是半径为r 的圆,假设雨区的质心和圆中心重合,预报和观测雨区的中心距离为d,通过调节r 值和d 值的大小可分别设定不同干湿偏差和雨区位移偏差的预报情形。这里的干(湿)偏差是指降水预报的面积小于(大于)降水观测的面积,对应频率偏差小于(大于)1。设置两种雨区位移偏差情形(图2):(1)d=0.5,代表小位移偏差;(2)d=1.5,代表大位移偏差。此外,设定4 种干湿偏差情形(图2):(1)FB=0.5,代表强干偏差;(2)FB=0.8,代表弱干偏差;(3)FB=2.0,代表强湿偏差;(4)FB=1.2,代表弱湿偏差。由于FB 等于预报雨区和观测雨区的面积比,即FB=r2,故设定FB 值与设定半径r 值等效。
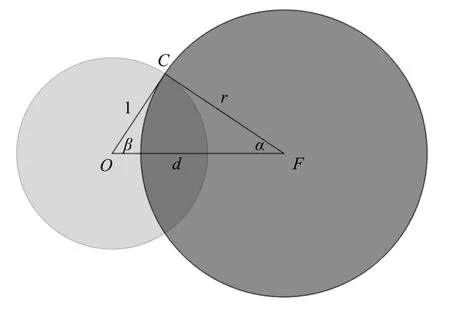
图1 理想模型 (其中实况雨区是圆心为O 的单位圆,预报雨区是圆心为F 半径为r 的圆,预报和观测雨区的圆心距为d)Fig. 1 An ideal model (the unit circle O is the observed rain area and circle F with a radius of r is the forecast rain area,the central distance between forecast and observed rain areas is d)
图2 给出了不同位移和干湿偏差情形下,原始降水预报、频率匹配与最优TS 评分法对应的理想模型以及理想模型的TS、频率偏差评分。由于是理想模型分析,这里的最优TS 评分法不设置订正系数的限制。从图2 可以归纳出以下几点:(1)频率匹配法订正消除了干湿偏差(FB=1),而最优TS 评分法订正总是伴随着湿偏差(FB>1,严格地讲最优TS 评分法仅当d=0 时FB=1),且原始预报的位移偏差越大,最优TS 评分法订正的湿偏差越大;(2)当原始预报位移误差较小时,频率匹配法与最优TS 评分法订正的TS 评分差异不大,都能显著改进除弱湿偏差以外的原始预报的TS 评分;(3)当原始预报的位移偏差较大时,频率匹配法仅能改进干偏差情形的TS 评分,而最优TS 评分法可以改进所有干湿偏差情况的TS 评分。
图3a 给出了不同位移偏差d 情形下,理想模型的TS 评分随预报雨区半径(r)的变化。可以看出,TS 评分峰值对应的预报雨区半径r 总是大于1(仅当d=0 时TS 峰值对应的r=1),与图2 中最优TS 评分法总是伴随湿偏差一致。对于较小的位移偏差d=0.5(图3a 黑色实线):频率匹配法订正(r=1)的TS 评分接近TS 峰值,与最优TS 评分法订正的TS 评分差异不大;而弱的湿偏差(r 略大于1)对应的TS 评分也接近TS 峰值,因此频率匹配和最优TS 评分法难以改进包含弱湿偏差的原始预报的TS 评分。对于较大的位移误差d=1.5(图3a 点划线):TS 评分在干偏差区间(0,1)上单调递增,因此频率匹配订正(r=1)能改进干偏差情形的TS 评分;而在湿偏差区间(1,3.58)上的TS 评分均不低于r=1 时的TS 评分,因此频率匹配法难以在原始预报包含湿偏差时提升TS 评分。图3b 给出了最优TS 评分(TSmax)及相应的预报雨区半径(rOTS)、频率偏差(FBOTS)随位移偏差d 的变化。可见,随着d 的增大,最优TS 评分法订正的湿偏差(FBOTS)也随之增大,且订正后的最优TS 评分(TSmax)也迅速下降。
3.2 订正个例

图2 不同位移偏差和干湿偏差情形下,原始预报、频率匹配、最优TS 评分法对应的理想模型 (观测:浅色阴影,预报:深色阴影),以及理想模型的TS 评分和频率偏差评分 (其中的最优TS 评分不设置订正系数的限制)Fig. 2 Ideal model (observation:light shaded,forecast:dark shaded) and its TS,FB of RAW,FMM and OTS under different displacement bias d and dry/wet biases situations (the OTS has no limitations for calibration coefficient)
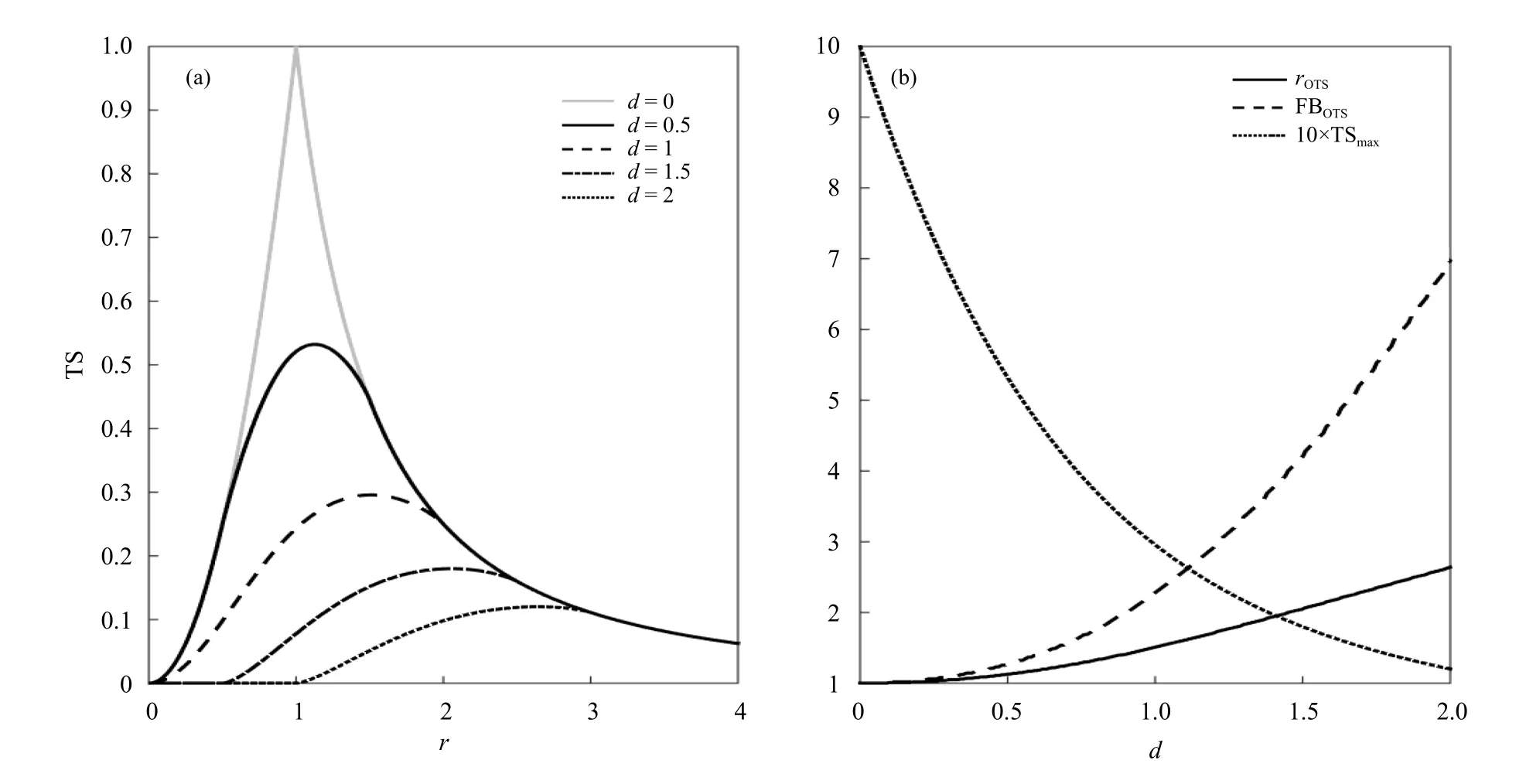
图3 (a) 不同位移偏差d 情形下,理想模型的TS 评分随预报雨区半径(r)的变化,(b) 最优TS 评分 (TSmax)及相应的预报雨区半径 (rOTS)、频率偏差 (FBOTS) 随位移偏差d 的变化Fig. 3 (a) Under different displacement bias d,TS as a function of the radius r of forecast rain area in the ideal model;(b) the optimal TS (TSmax),the corresponding radius of forecast rain area (rOTS),and frequency bias (FBOTS)as a function of the displacement bias d
为了进一步直观理解4 种订正方法的基本特性,本节采用2019 年第11 号台风“白鹿”的强降水(8 月25 日08 时—26 日08 时)个例进行订正展示。图4 给出了2019 年8 月22 日20 时(北京时)起报的60—84 h 原始降水预报、4 种降水预报订正产品和相应的实况,由站点降水通过反距离权重插值到格点上。表2 给出了该个例中原始降水预报和4 种降水预报订正产品在图示区域内站点的暴雨(50 mm/d)检验评分。可以看出,原始预报(图4a)相比于实况(图4f)存在偏北的位移误差,且在暴雨量级上存在弱的干偏差,频率偏差为0.81(表2)。经频率匹配和最优TS 评分订正后,暴雨雨区有所扩大而小雨雨区有所减小(图4b、c),雨区面积更接近实况,频率偏差更接近1(表2),TS 评分也有明显提升。这一点与3.1 节中理想模型分析的“频率匹配和最优TS 评分法均能提升干偏差情形的TS 评分”一致。需要注意的是,频率匹配与最优TS 评分法仅能订正雨带的量级,无法订正雨带的位移误差,因此在提升TS 评分和降低漏报率的同时,也存在虚警率略偏大的问题(表2)。最优百分位法则基于历史集合预报与实况资料计算出该个例对应的历史训练期TS 评分最大的集合百分位为90%,故最优百分位法对该个例订正的结果为原始集合预报的90%集合分位数(图4d)。从表2 中可以看出,虽然最优百分位法的TS 评分最高、漏报率最低,但由于雨区面积过大(图4d)也导致虚警率最高。简单的集合平均由于平滑作用常常导致强降水预报的降水量级偏低,而概率匹配法既保留了集合平均的空间分布,又参考了集合成员的降水量级。图4e 为概率匹配法订正的降水预报,具有强降水落区向集合平均中心集中的特征。由于概率匹配法不使用历史资料训练,在本个例中无法根据历史系统偏差对集合预报进行订正,因此对暴雨的量级预报偏弱,订正效果不佳(表2)。综合对比4 种订正法的降水落区,可以看出频率匹配和最优TS 评分法主要改变原始预报的降水量级而并不改变落区,最优百分位与概率匹配法由于使用了集合预报信息可同时改变原始预报的降水量级和落区。
4 总体检验评估
4.1 全年预报性能
小雨量级(图5),原始模式预报存在较强的湿偏差,不同预报时效的频率偏差都在1.5 以上。频率匹配法订正显著消除了小雨的强湿偏差,不同预报时效的频率偏差都接近1。虽然频率匹配法订正后总体的雨区面积与实况较一致,但对小雨的漏报率很高,可以推断这是由于雨区的位移偏差较大造成的。最优TS 评分和最优百分位法在一定程度上减小了小雨的湿偏差,而概率匹配法反而略增大了原始模式的湿偏差。这是由于概率匹配法未引入历史实况信息对原始预报的湿偏差进行修正,而是利用集合预报直接生成定量降水预报产品。从频率匹配法的频率偏差和漏报率随预报时效的变化分析可知,雨区的总体面积保持不变的情况下漏报率不断增大,说明雨区的位移偏差随预报时效的延长不断增大。因此,在较长预报时效下,原始预报除了湿偏差还伴随着较大的位移误差,结合理想模型的分析结论“当原始预报的位移偏差较大时,频率匹配法仅能改进干偏差情形的TS 评分”可知,频率匹配法无法在较长预报时效下改进小雨的TS 评分,这一点也从TS 评分随预报时效的变化图(图5b)上得到了印证。最优TS 评分法的TS 评分在1.5—5.5 d 预报时效下正技巧最高,而在更长的预报时效下TS 评分不如最优百分位和概率匹配法,这是由于随着预报时效的进一步延长,预报的不确定性增大,集合预报相比确定性预报的优势逐渐凸显。考虑到最优百分位法相比概率匹配法增加了历史实况信息,因此最优百分位法在各个预报时效下TS评分的表现好于概率匹配法。

图4 2019 年8 月22 日20 时起报的60—84 h 原始降水预报 (a)、频率匹配法订正 (b)、最优TS 评分法订正 (c)、最优百分位法订正 (d) 和概率匹配法订正 (e) 的结果以及2019 年第11 号台风“白鹿”的强降水 (8 月25 日08 时—26 日08 时)实况 (f)Fig. 4 Observation (f),the 60—84 h RAW (a) precipitation forecasts initialized at 20:00 UTC 22 August 2019,using FMM (b),OTS (c),OP (d) and PM (e) calibration during the heavy rain (08:00 BT 25—08:00 BT 26 August)of Typhoon Bailu (1911)

表2 2019 年第11 号台风“白鹿”的强降水个例的原始预报、频率匹配、最优TS 评分、最优百分位和概率匹配法的暴雨 (50 mm/d) 检验评分Table 2 Verification scores of torrential rain (50 mm/d) of RAW,FMM,OTS,OP,and PM in the heavy precipitation event of Typhoon Bailu
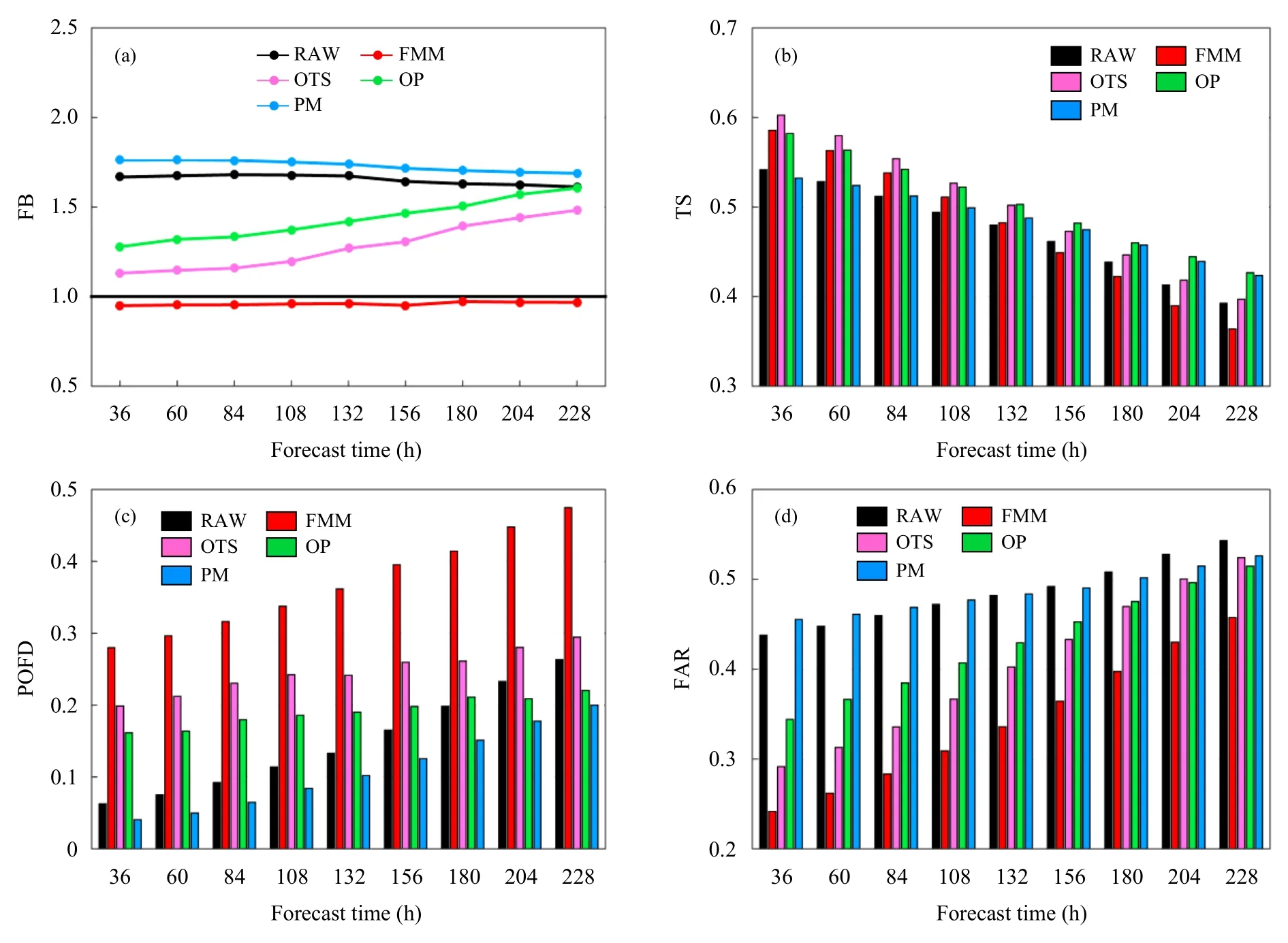
图5 原始预报、频率匹配、最优TS 评分、最优百分位和概率匹配法全年不同预报时效小雨量级 (0.1 mm/d) 的频率偏差 (a)、TS 评分 (b)、漏报率 (c) 和虚警率 (d)Fig. 5 Annual frequency bias (a),threat score (b),probability of false detection (c) and false alarm ratio (d) of light rain(0.1 mm/d) for RAW,FMM,OTS,OP,and PM at different lead times
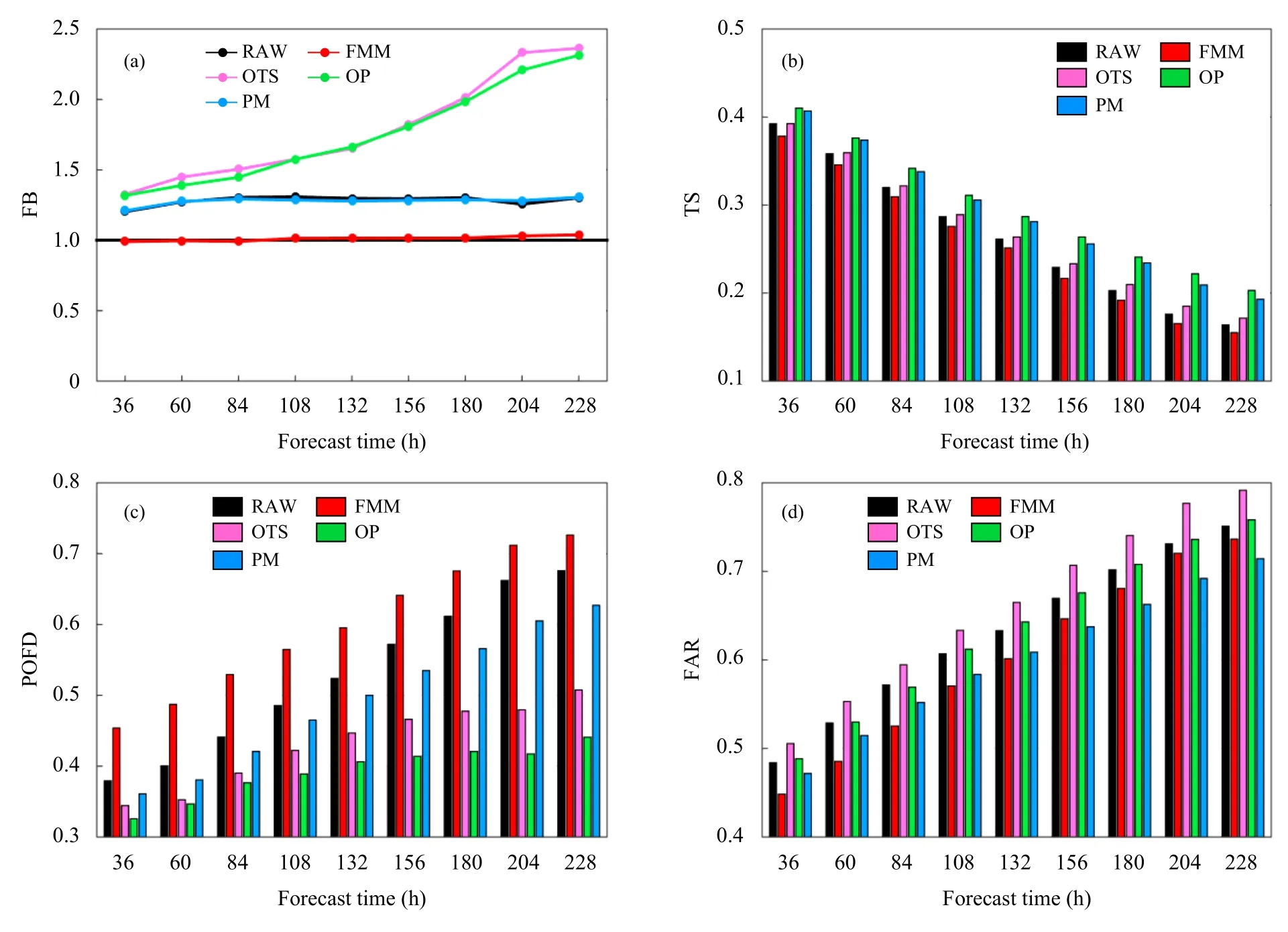
图6 与图5 相同,但为中雨量级 (10 mm/d)Fig. 6 Same as Fig. 5 but for moderate rain (10 mm/d)
中雨量级(图6),原始模式预报存在较弱的湿偏差,不同预报时效的频率偏差都在1.3 左右。频率匹配法订正显著消除了中雨的弱湿偏差,不同预报时效的频率偏差都接近1。根据理想模型的结论可以判断频率匹配法无法改进弱湿偏差情形下的TS 评分,这一点从图6b 中也得到了印证。概率匹配法的频率偏差与原始预报一致,而最优TS 评分和最优百分位法均呈现较大的湿偏差,且随预报时效的延长而增大。这一点也可以通过理想模型进行解释,由于最优TS 评分与最优百分位法都以TS 评分最优为目标,因此总是伴随着湿偏差,且雨区的位移偏差越大,湿偏差越大。虽然最优TS 评分法对强降水的订正系数进行了范围限制(35 mm/d以上降水的订正系数限制在0.8—1.6),但雨区面积随降水阈值并非线性变化,订正前、后雨区面积的增长倍数可大于降水量增长的倍数。此外,还可以看出集合预报对于存在较弱湿偏差的中雨量级降水预报体现了明显的优势,最优百分位和概率匹配法相比原始预报在没有增大虚警率和漏报率的情况下,提升了所有预报时效的TS 评分,这得益于集合预报信息的加入,而仅通过对确定性预报进行量级订正(频率匹配和最优TS 评分法)无法显著改进原始预报。
大雨量级(图7),原始预报频率偏差接近1,几乎不存在系统偏差,此时频率匹配法无法改进原始预报。最优TS 评分法虽然略微改进原始预报的TS 评分,但也伴随着强的湿偏差和虚警率最高的问题。基于集合预报的最优百分位和概率匹配法再一次发挥了优势,但两者的表现有所不同。最优百分位法倾向于增加一定的湿偏差来达到TS 评分的最大,与最优TS 评分法相比,最优百分位法的湿偏差与之量级相当,但TS 评分、漏报率和虚警率均好于最优TS 评分法。这是由于集合预报信息的引入在一定程度上修正了确定性预报的落区。概率匹配法在不同评分上的表现较为平衡,没有明显的干湿偏差,且TS 评分、漏报率、虚警率比原始预报均有改进,尤其是虚警率的降低最明显,这再一次体现了集合预报的优势。
暴雨量级(图8),原始预报存在较弱的干偏差。频率匹配法仍然具有4 种订正方法中最优的频率偏差,但相比小雨、中雨和大雨那样近乎完美的频率偏差,暴雨仍存在微小的湿偏差。这是由于暴雨量级的训练样本较少,频率偏差存在年际变化,或是由于模式升级更新导致在该量级降水预报的系统偏差出现了微小的变化。频率匹配法改进了1.5—5.5 d预报时效的暴雨TS 评分,与理想模型的结论“频率匹配可以改变干偏差情形的TS 评分”一致。对于更长的预报时效,原始预报的频率偏差接近1,但漏报率、虚警率都显著增大,说明暴雨的位移误差也显著增大,甚至出现较多原始预报与实况没有重叠雨区的情况,此时频率匹配法因保持雨区面积与实况一致而无法提升TS 评分,最优TS 评分法通过适当的扩大雨区范围增加与实况雨区的重叠面积在一定程度上提升了TS 评分。需要注意的是,由于最优TS 评分法增加了订正系数的范围限制,因此湿偏差并不是很大。同时,测试了不加订正系数范围限制的最优TS 评分,发现对小雨、中雨、大雨都没有影响(因为都小于35 mm/d),而对暴雨的频率偏差与最优百分位法类似存在很大的湿偏差,且可进一步提升TS 评分,但提升之后TS 评分总体上仍低于最优百分位法(图略)。最优百分位法虽然显著提升了不同预报时效的TS 评分,但也存在湿偏差和虚警率过大的问题。概率匹配法对暴雨的干偏差比原始预报还大,说明在暴雨量级上集合预报本身相比实况仍然量级偏低,因此无法改进暴雨的预报性能。
4.2 季节预报性能
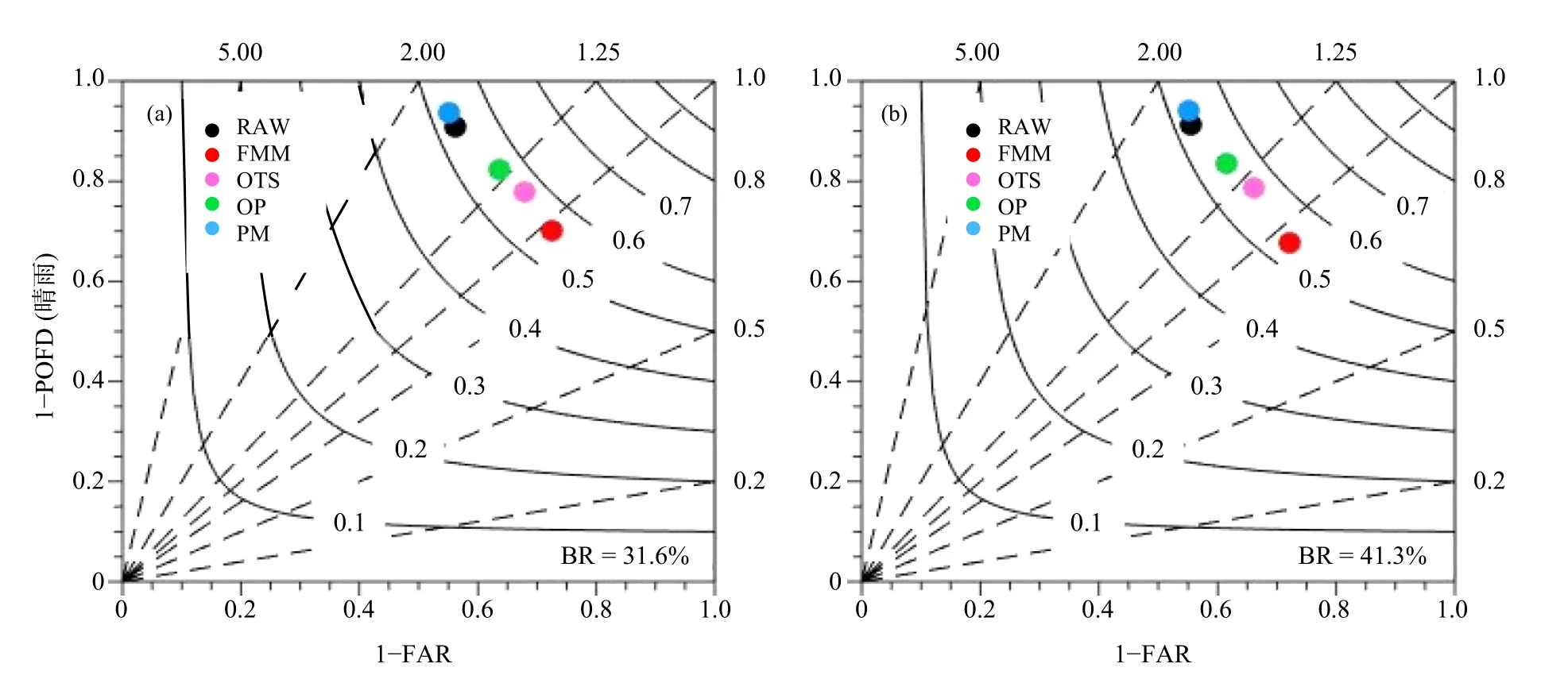
图9 不同季节 (a、e、i、m. 春季,b、f、j、n. 夏季,c、g、k、o. 秋季,d、h、l、p. 冬季)、不同降水量级 (a—d. 小雨,e—h. 中雨,i—l. 大雨,m—p. 暴雨) 的原始预报、频率匹配、最优TS 评分、最优百分位和概率匹配法的性能(BR 为样本的基础观测覆盖率)Fig. 9 Performance diagrams of RAW,FMM,OTS,OP and PM for different seasons (a,e,i,m. spring;b,f,j,n. summer;c,g,k,o. autumn;d,h,l,p. winter) and rain thresholds (a—d. light rain (0.1 mm/d),e—h. moderate rain (10 mm/d),i—l. heavy rain (25 mm/d),m—p. torrential rain (50 mm/d))(BR is the sample base rate)
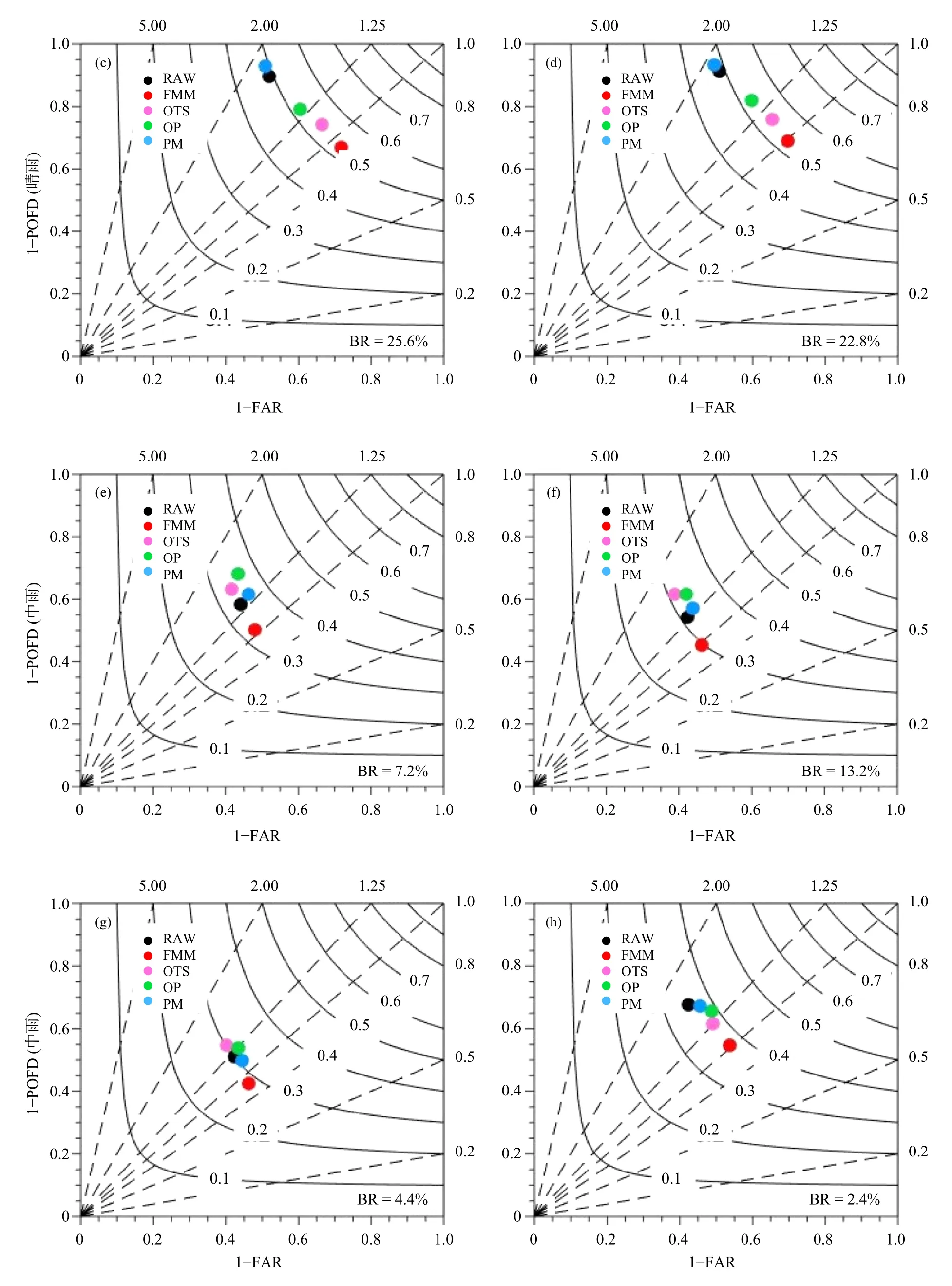
续图9 Fig. 9 Continued
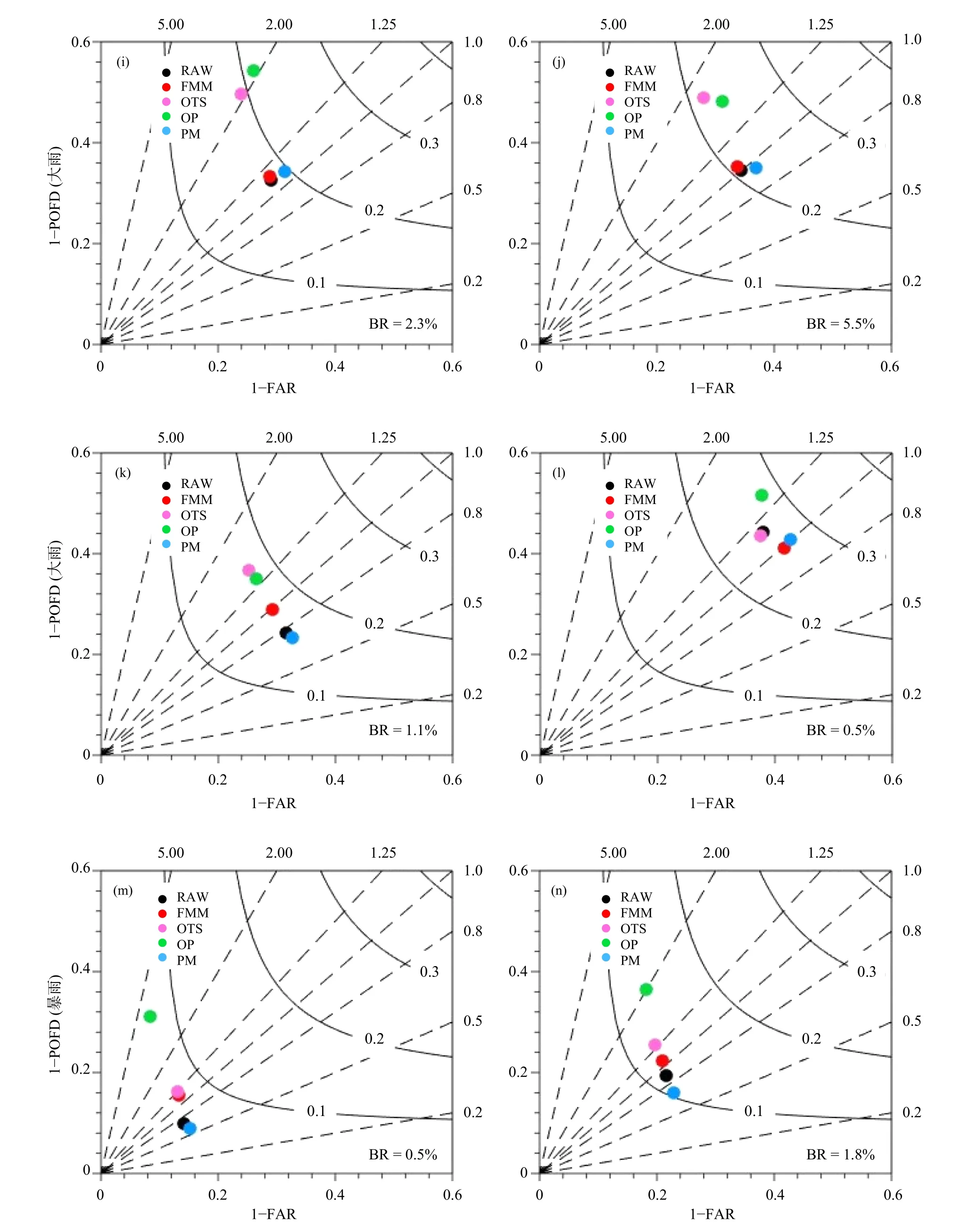
续图9 Fig. 9 Continued
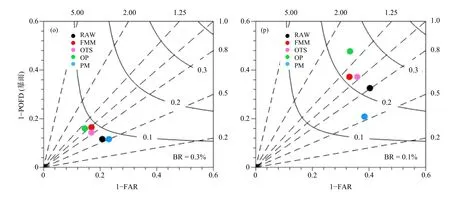
续图9 Fig. 9 Continued
评估不同定量降水预报客观订正方法在不同季节的预报性能表现,对于实际业务更具指导意义。图9 给出以60—84 h 预报时效为例进行的性能检验评估,同一张图上可同时展示4 种检验评分的结果,其中实曲线代表TS 评分等值线,虚直线的斜率为频率偏差,横坐标为1−虚警率(FAR),纵坐标为1−漏报率(POFD)。从实况基础覆盖率(BR)可以看出,不同等级的降水覆盖率排序都是夏季>春季>秋季>冬季。总体来看,频率匹配法在不同季节、不同降水等级情形下的频率偏差都是最优的,最接近对角线,有效减小了原始预报雨区面积的系统偏差。对于晴雨(同小雨),实况样本量比较充足,即使样本量最低的冬季观测覆盖率也达到了22.8%(图9d),不同季节的评估结果也具有相似性。频率匹配、最优TS 评分和最优百分位法都对原始预报的TS 评分有小幅度提升,同时降低了原始预报的湿偏差,减小了虚警率但增大了漏报率,其中频率匹配法的虚警率和漏报率达到平衡,结论与全年检验结果一致。对于中雨,最优百分位和概率匹配法对原始预报的TS 评分有小幅度提升,其中最优百分位法的提升幅度略大一些。最优百分位法在降水较多的春、夏两季湿偏差比原始预报还大,秋季与原始预报一样,而降水较少的冬季减小了原始预报的湿偏差。对于大雨,原始预报在春、夏两季不存在干湿偏差,而秋季略偏干,冬季略偏湿。最优百分位法对原始预报的TS 评分提升最大,但总是伴随着湿偏差,尤其在春季频率偏差达到了2。对于暴雨,秋、冬两季出现的频率很低,观测基础覆盖率分别为0.3%和0.1%。从春、夏两季来看,频率匹配和最优TS 评分法在改进了原始预报的TS 评分的同时,维持了较好的干湿偏差。虽然最优百分位法对夏季暴雨的TS 评分提升最大,但湿偏差也明显,雨区总面积达到了观测的2 倍。
4.3 不同订正方法的经济价值模型评估
图10 以60—84 h 预报时效为例,从参考不同预报产品进行风险决策所产生经济价值的角度,对4 种定量降水预报客观订正方法进行评估。对于小雨(图10a),当花费/损失在0.05—0.2 时,只有概率匹配法的经济价值高于原始预报,而当花费/损失在0.5—0.7 时,另外3 种订正方法产生了比原始预报更高的经济价值,从大到小依次是频率匹配、最优TS 评分和最优百分位法。最优百分位法在中雨、大雨和暴雨的风险决策中体现了较大的参考价值(尤其是暴雨),经济价值分别在花费/损失区间0.05—0.3、0.02—0.2、0.01—0.1 上高于其他预报方法。需要注意的是,当经济价值为负值时,所有预报产品在风险决策中都失去了参考价值。以暴雨为例,当花费/损失大于0.2 时,无论参考那种预报产品进行风险决策,所产生的经济价值都是负效果。其他预报时效的结论与60—84 h 时效一致(图略)。
5 结论与讨论
重点对比了频率匹配、最优TS 评分、最优百分位、概率匹配4 种定量降水预报客观订正方法的特性和预报性能。通过构建理想模型研究了频率匹配和最优TS 评分法在不同位移和干湿偏差情形下的基本特征。选取典型降水个例,评估了4 种定量降水预报客观订正方法在全年、不同季节、不同预报时效、不同降水量级下的表现,以及在风险决策中的经济价值。表3 归纳了不同订正方法的基本原理,以及2019 年在中国站点上的预报订正效果,包括不同降水量级下的频率偏差、预报技巧等信息。得出以下主要结论:
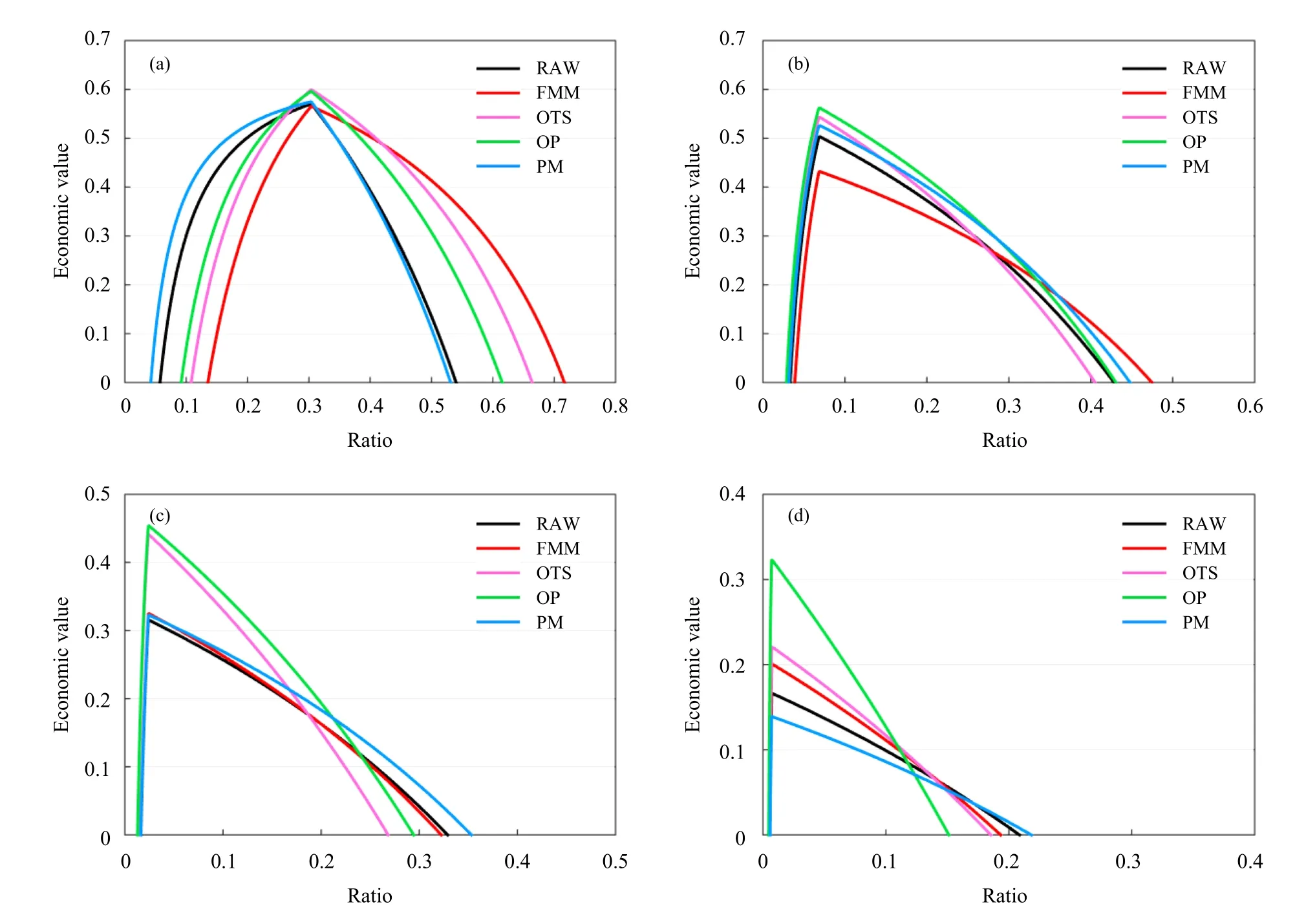
图10 60—84 h 时效的原始预报、频率匹配、最优TS 评分、最优百分位和概率匹配法在小雨 (a,0.1 mm/d)、中雨 (b,10 mm/d)、大雨 (c,25 mm/d) 和暴雨 (d,50 mm/d) 降水量级上的经济价值随花费/损失的变化Fig. 10 Economic values as a function of cost/loss for 60―84 h precipitation forecasts of RAW,FMM,OTS,OP and PM at light recipitation forecasts of RAW,FMM,OTS,OP and PM at light (a,0.1 mm/d),moderate (b,10 mm/d),heavy (c,25 mm/d)and torrential (d,50 mm/d) rain thresholds
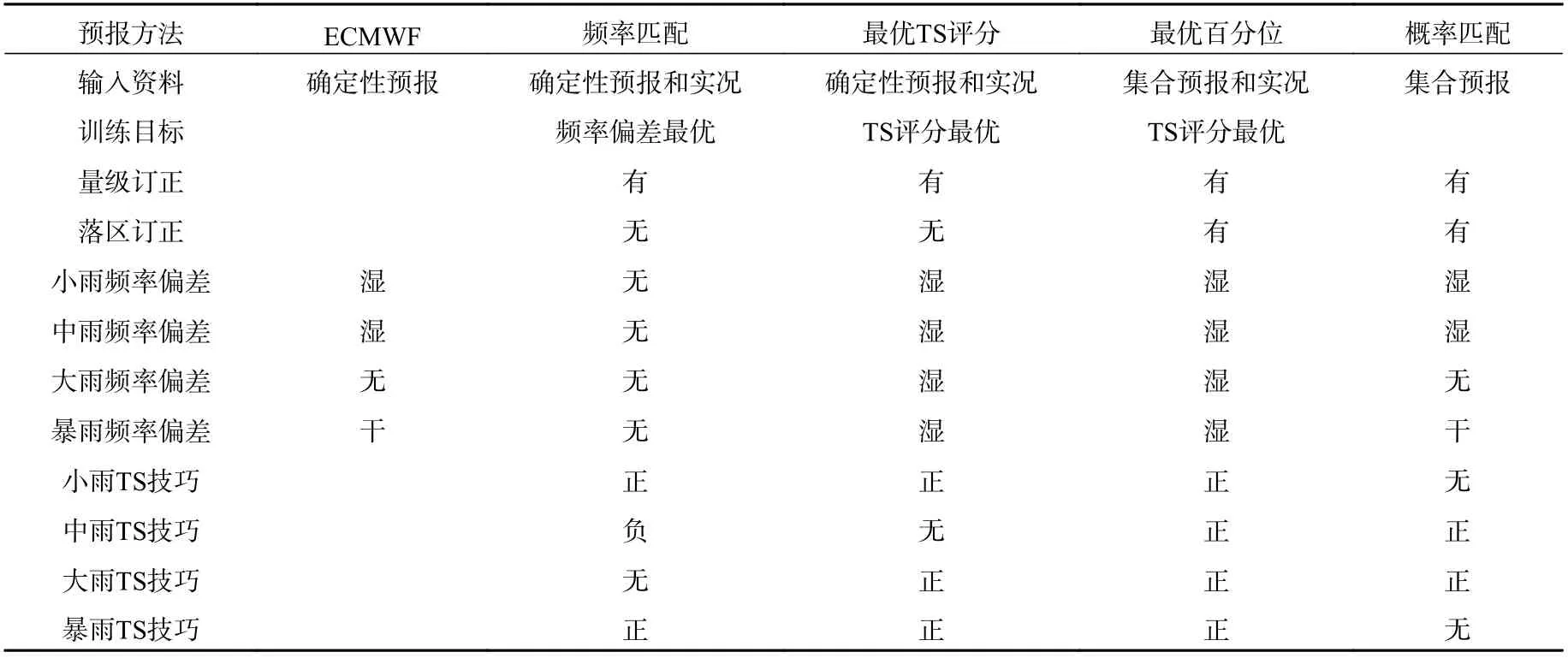
表3 ECMWF 原始模式预报及不同订正方法在2019 年中国2411 个气象站的逐日降水预报中的表现(TS 技巧是指预报产品的TS 评分与ECMWF 原始模式TS 评分之差,正值代表正技巧,负值代表负技巧)Table 3 Performance of the original ECMWF and four different calibration methods in the daily precipitation forecasts of 2411 meteorological stations during 2019 (The TS skill score indicates the difference of TS between the calibrated and the original ECMWF forecasts. Positive values represent skillful while negative values represent unskillful )
(1)ECMWF 确定性预报模式的整体降水系统偏差表现为:小雨存在较强湿偏差、中雨存在较弱湿偏差、大雨无干湿偏差、暴雨存在弱的干偏差。
(2)频率匹配和最优TS 评分法基于历史训练资料直接对确定性预报进行量级订正,无法订正原始预报的位移误差,因此降水落区的形态也与原始预报相似;最优百分位和概率匹配法均利用集合预报信息生成确定性预报产品,可以改变降水落区的形态。
(3)频率匹配法以频率偏差最优为训练目标,能有效地消除模式的干湿偏差;当雨区的位移误差较小且存在明显的干湿偏差时,频率匹配法可以提升TS 评分。以TS 评分最优为训练目标的最优TS 评分法和最优百分位法则表现为湿偏差,特别是春、夏两季最优百分位的湿偏差较大;最优TS 评分可在一定程度上提升小雨、大雨和暴雨的TS 评分,但无法改善中雨的TS 评分;最优百分位法显著提升了所有量级降水的TS 评分,这主要得益于集合预报信息的引入,在较长预报时效下的改进优势尤其凸显。概率匹配法虽然也使用集合预报信息,但没有利用历史实况对集合预报进行订正,因此仅能在一定程度上改进大雨、中雨和较长预报时效小雨的TS 评分。
(4)不同定量降水预报客观订正方法的风险决策经济价值模型评估表明:对于小雨,概率匹配和频率匹配法在不同花费/损失区间上具有较高的经济价值;在中雨、大雨和暴雨的风险决策中,最优百分位法体现了较大的参考价值,尤其是暴雨。
以上4 种定量降水预报客观订正方法在模式雨带位移偏差较大时仍存在一定的局限性,此时最优TS 评分和最优百分位法常常伴随着显著的湿偏差,在实际业务使用时需要注意。虽然最优百分位和概率匹配法利用集合预报信息可在一定程度上改变降水落区的形态,但对雨带的位移偏差调整幅度还是非常有限,未来可尝试借助面向对象的检验评 估 方 法( Method for Object-based Diagnostic Evaluation,简称MODE)(Davis,et al,2006,2009)来改进订正雨带的位移偏差。此外,这4 种订正方法都是基于降水量本身建模的,未来可考虑引入更多的物理量和大数据信息,探索基于机器学习的定量降水预报客观订正方法。

