不同切角方柱斜切体驰振压电能量收集研究
王军雷,张程雲,陈卫哲,2,吴义鹏,王定标,靳遵龙
(1.郑州大学 机械与动力工程学院,河南 郑州 450001; 2.许昌市质量技术监督检验测试中心,河南 许昌 461000; 3.南京航空航天大学 机械结构力学及控制国家重点实验室,江苏 南京 210016)
0 引言
近年来,由于传统能源短缺和化石能源所造成的环境污染问题,研究可替代的、环境友好的能源获取方式具有较强的实际意义[1-3]。流体能是一种清洁可再生能源,同时流体诱发振动是一种常见的工程结构破坏现象[4]。随着微能量收集技术的快速发展,如纳米摩擦发电机技术[5-7]和利用压电效应将流致振动机械能转换为电能已成为微机电领域可再生能源有效利用的重要方式[8-10]。在环境能量收集技术方面,基于风致振动效应的微型风力俘能器是研究的热点[11]。微型风力俘能装置能够将自然环境中的风能转化为电能并加以储存,同时具有体积小、可持续以及可无人操控等优势,从而能够克服传统大型风力装置的局限性,在环境保护、建筑安全以及交通系统中具有较高的实用价值[12-13]。
近年来在风能俘获利用方面,微型压电振动俘能装置具有巨大的发展潜力和广阔的应用前景,因而被学者们广泛研究[14-16]。Wang等[17]提出了一种基于CFD方法结合机电模型对压电俘能器性能进行预测的方法,并通过实验验证了该方法的有效性,得到了电压输出的时程和频率响应以及能量收集系统的流动模式。练继建等[18]进行了正方形截面振子的流致振动试验研究,分析了振子在不同来流角度下的振动响应,探讨了系统刚度和质量对振动振幅和频率的影响,其研究结果对流致振动能量收集器的设计具有一定的指导作用。为提出一种新型高性能压电式风能俘能器,Wang等[19]通过在钝体上添加“Y型”附件得到Y型驰振压电能量收集器(GPEH-Y)的理论模型,同时采用格子玻尔兹曼方法(LBM)对振动幅值和频率进行了分析,确定了涡激振动向驰振的过渡过程,并通过一系列风洞实验验证了所提出的GPEH-Y模型。进一步地,针对双压电式风能俘能器的设计,HU等[20]研究并发现在相互干扰下双俘能器之间的相对位置对其发电效率至关重要,并通过试验研究了两种俘能器串联或交错布置时的能量产生情况,确定了最佳相对位置,以提供最佳的输出功率。同时,Wang等[21]研究了具有不同顶角的三角形截面钝体GPEH,基于CFD数值模拟方法确定了其气动力响应特性,并使用实验对其进行了验证,最终得出钝角β=130°为性能最优的顶角。丁林等[22]研究了不同参数钝体形状和压电片长度对钝体风致振动响应及其能量转换特性的影响,验证了驰振理论模型。结果表明:方柱钝体相比于梯形柱、圆柱和三角柱,其起振折减速度最低,振幅响应最大,能量输出最高,系统的输出电压和功率随压电片长度的增加而增大。李恒[23]研究了不同截面形状的钝体在高雷诺数(1×104≤Re≤1.2×105)下流致振动的振幅、频率以及尾流响应,得到不同截面形状钝体的俘能效果对比。结果表明:梯形柱、三角柱、方柱和菱形柱的俘能效果依次增强,且方柱攻角、三角柱顶角的增加以及菱形柱轴比例的减小会抑制驰振的产生。梁盛平等[24]提出了一种附着在圆柱钝体上的鱼尾状仿生结构,对流致振动的控制进行实验研究。结果表明:当附加仿鱼尾结构时,圆柱的振动会被部分抑制,且随着仿鱼尾结构尾部长度的增加,抑制效果逐渐增强。
上述研究钝体外型设计对GPEH的性能提升具有决定性作用。然而,目前针对带有斜切角度的钝体作为绕流钝体进行能量采集的研究还相对较少。本文建立了光滑方柱和不同斜切角度的方柱斜切体(θ=30°、45°、60°)的原型机模型,通过一系列风洞实验,研究了具有不同斜切角度的方柱钝体对压电俘能器性能的影响,为钝体驰振压电俘能装置的设计和优化提供理论与实践基础。
1 实验参数测定
驰振通常被认为是一种准定常自激振动,在一定风速下气动力作用于具有尖锐棱角的钝体时,产生空气动力负阻尼,对结构做正功,引发一种气动弹性不稳定现象。因此,改变钝体几何特征对驰振压电俘能器的输出功率和电压具有重要影响。如图1所示,本文设计了一种“T字型”悬臂梁式压电俘能装置。将该装置置于直径为400 mm、长度为4 m的圆形风洞中,基于蜂窝状结构对来流风进行稳风。悬臂梁与钝体垂直安装在纯铝制的固定装置上,其阻塞率约为4.7%,小于临界值5%[25],对实验结果影响较小。使用导线将电阻负载接入电路。压电片(PZT-5)的尺寸为35 mm×10 mm×0.3 mm,置于悬臂梁顶部。悬臂梁为铝制金属薄片,有效长度为132 mm。通过数字示波器(ISDS220B)对钝体振动产生的简谐波进行采集。通过调频器调节风机频率,从而对风速大小进行控制。

图1 实验装置示意图Figure 1 The diagram of experimental setup
图2(a)为物理模型图。风向垂直于钝体轴线方向,当空气流过方柱钝体时,方柱后方流体会形成周期性的旋涡,旋涡的脱落会引发钝体产生周期性的升阻力。随着风速增大,当旋涡脱落的频率接近钝体的固有频率时,方柱钝体会发生剧烈振动。但由于方柱钝体安放在悬臂梁末端,方柱钝体振动所产生的位移主要发生在y轴方向,z轴方向上不发生位移,x轴方向上的位移可以忽略,因此可以将整个振动能量收集系统简化为如图2(b)所示的M-C-K单自由度振动系统,悬臂梁等效为弹簧振子。图2(c)为本文所设置的不同倾角方柱斜切体的正视图,图中侧面和斜切面之间的倾角θ分别为30°、45°和60°。同时本文设置一组光滑方柱钝体的对照实验,研究方柱斜切体不同倾角对驰振压电俘能器俘能效果的影响。

图2 钝体驰振机理示意图Figure 2 Schematic of galloping energy harvesting system
系统控制方程和机电耦合方程可以分别表示为:
(1)
(2)

其中M-C-K振动系统参数可以表示为:
Meff=(33/140)md+ml;
(3)
Ceff=2ζωnMeff;
(4)
(5)
式中:md为悬臂梁质量;ml为钝体质量;ζ为阻尼比;ωn为系统的固有圆频率。
机电耦合系数可以表示为:
(6)
式中:ωoc为开路圆频率;ωsc短路圆频率。
通过自由衰减实验得到开路和短路频率大小分别为8.72 Hz和8.715 Hz,代入式(6)得到机电耦合系数为2.228×10-5N/V。表1中列出了M-C-K振动系统的相关参数值。

表1 M-C-K系统参数Table 1 Parameters of M-C-K system
在准静态条件下,系统所受空气动力Fy(t)的表达式为:
Fy(t)=0.5ρAyU2CFy(t)。
(7)
式中:ρ为来流空气的密度;U为来流风速;Ay为方柱钝体在垂直于风向截面上的投影面积;CFy(t)为空气动力系数,可表示为:
(8)

Meffy(t)+Keffy(t)+γV(t)=0。
(9)
当i=1时,系统阻尼项为Ceff-0.5ρAyUm1。此时系统阻尼项为线性,非线性项较小,可被忽略;当i>1时,系统阻尼项则以非线性的形式存在。假设临界风速为Ucr,则当U
2 结果分析
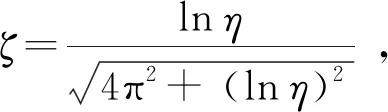

图3 自由衰减实验结果Figure 3 The result of free-decay experiment

图4 不同风速下输出功率随电阻变化Figure 4 Variation of output power with different resistance under different wind speed
本文对不同斜切角度的方柱斜截体驰振压电俘能器的俘能特性进行研究。将切面与侧面之间的夹角θ分别设为30°、45°和60°,分析对比3个不同斜切角以及光滑方柱驰振压电俘能器的俘能特性。图4为风速U=2.509 m/s和U=2.646 m/s时光滑方柱压电俘能器的输出功率随负载电阻的变化曲线。从图4中可以看出,电阻一定时,压电俘能器的输出功率随着风速的增大而增大。在相同风速下,随着电阻的增大,压电俘能器的输出功率先增大后减小。当R=0.6 MΩ时,风速U=2.509 m/s和U=2.646 m/s时的输出功率同时达到了最大值,分别为0.001 7 mW和0.002 5 mW,从而可以得到压电俘能器的最优负载为0.6 MΩ。
图5为开路电压和最优负载下的光滑方柱的输出电压均方根随风速增大的变化,可以看出,开路和最优负载下的输出电压均随风速的增大而增大,且在开路下的输出电压随风速增长的曲线的斜率远大于最优负载下的曲线斜率。当风速较小时,二者输出电压较为相近;当风速达到3.19 m/s时,二者输出电压相差较大,开路和最优负载下的输出电压分别为4.252 V和1.951 V。

图5 开路电压和最优负载下电压随风速变化Figure 5 Variation of open circuit voltage and voltage under optimal load with different wind speed
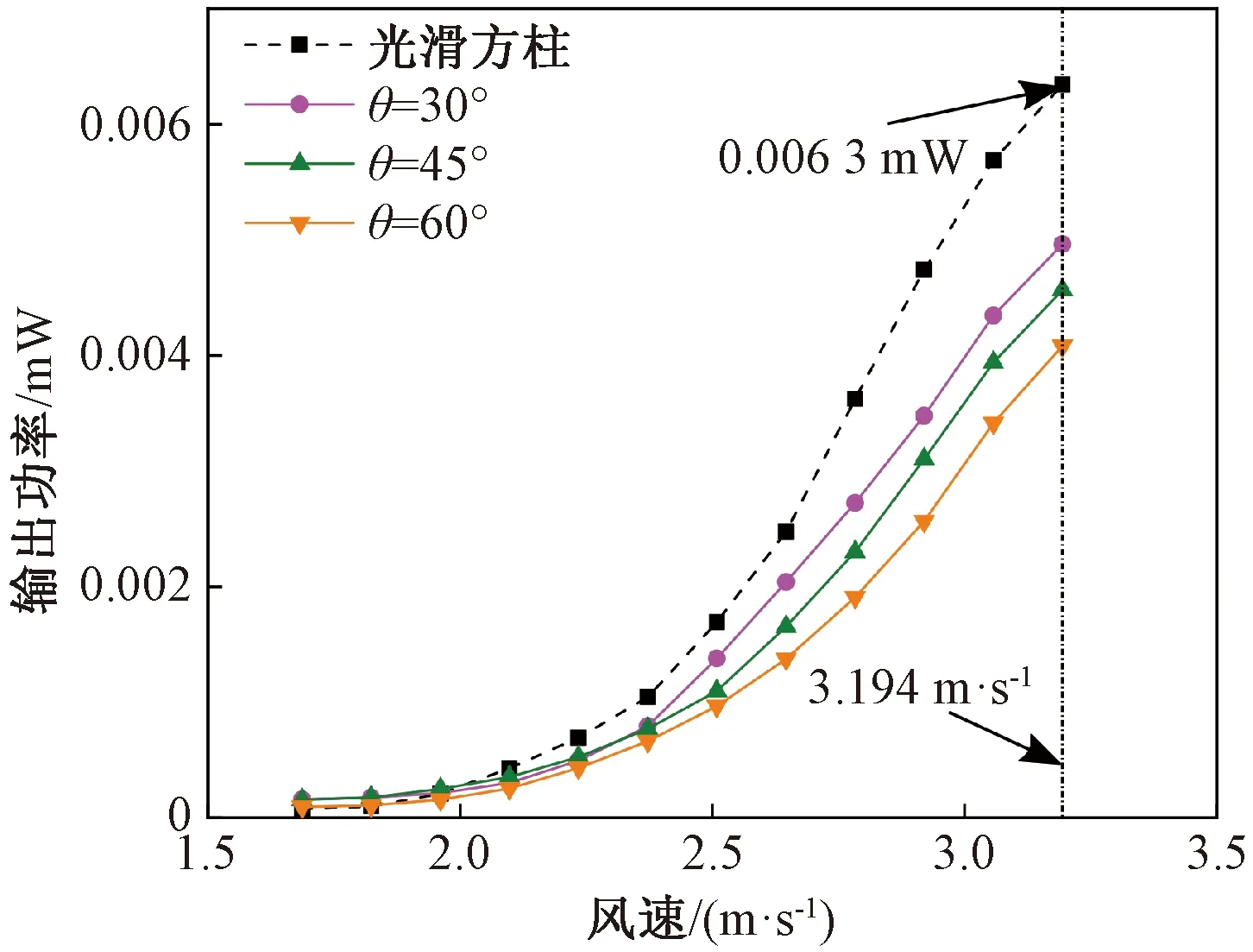
图6 不同钝体输出功率随风速变化Figure 6 Variation of output power of different bluff bodies under different wind speed
图6表示在最优负载R=0.6 MΩ时,方柱斜切体(θ=30°、45°、60°)以及光滑方柱的输出功率随风速变化的曲线。由图6可以看出,光滑方柱和方柱斜切体(θ=30°、45°、60°)的输出功率均随着风速的增大而增大,输出功率的增长率均先增大后减小。光滑方柱曲线的斜率最大,在相同风速下,光滑方柱的输出功率大于方柱斜切体的输出功率。当风速较小时,光滑方柱和方柱斜切体的输出功率相差较小;当风速达到U=3.194 m/s时,光滑方柱的输出功率为0.006 3 mW,分别是斜切角度θ为30°、45°和60°的方柱斜切体的1.28倍、1.39倍和1.55倍。相同风速下,斜切体中斜切角度θ=30°方柱斜切体输出功率最大,θ=45°时次之,θ=60°时输出功率最小。
图7为方柱斜切体(θ=30°、45°、60°)和光滑方柱的输出电压随风速变化的曲线。从图中可以看出,在标准交流接口下驰振压电俘能器的输出电压随着风速的增大而增大,且增长率随着风速的增大先增大后减小。其输出电压的变化曲线和输出功率的变化曲线趋于一致:在相同风速下,光滑方柱的输出电压大于方柱斜切体的输出电压;随着斜切角θ(30°、45°、60°)的增大,其输出电压逐渐减小。当风速达到U=3.194 m/s时,光滑方柱的输出电压为1.951 V,分别是斜切角度θ为30°、45°和60°的方柱斜切体的1.13倍、1.18倍和1.25倍。
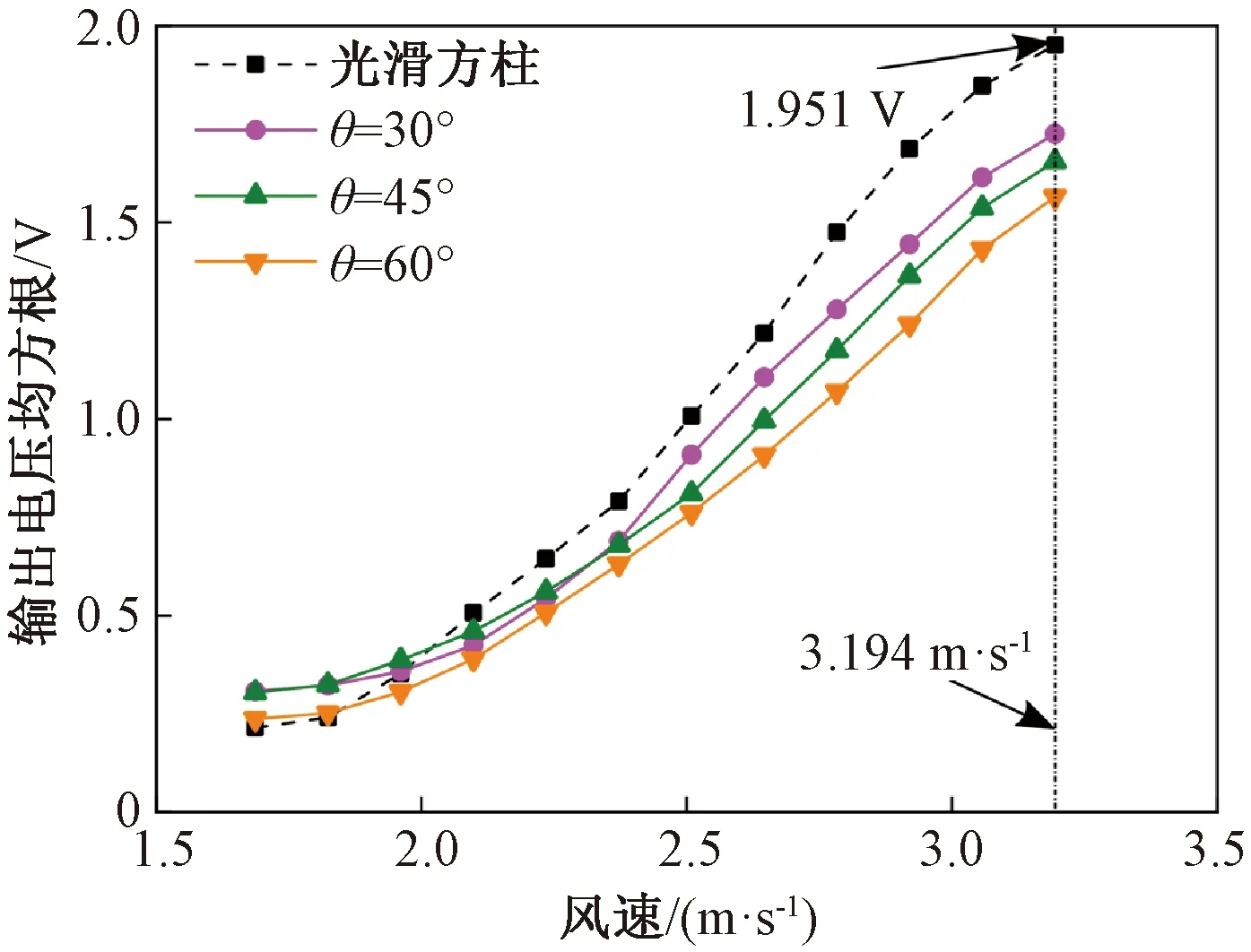
图7 不同钝体电压随风速变化Figure 7 Variation of voltage output of different bluff bodies under different wind speed
3 结论
针对不同斜切角的方柱斜切体驰振压电俘获器进行建模,借助风洞实验进行了实验研究。采用该模型对方柱斜切体切角θ分别为30°,45°和60°的驰振压电俘能器在不同风速和负载电阻下的输出电压和输出功率进行了分析,得出以下结论:
(1)基于风洞实验研究,测得最优负载为R=0.6 MΩ,在相同风速下,最优负载下的输出功率远小于开路电压下的输出功率。
(2)在最优负载R=0.6 MΩ下,光滑方柱和方柱斜切体的能量输出随风速的增大而增大,增长率先增大后减小。在相同风速下,光滑方柱的输出电压和功率大于方柱斜切体。
(3)在相同风速下,随着方柱斜切体切角θ(30°、45°、60°)的增加,方柱斜切体的输出电压和功率均减小。

