关于库存产品质量水平评估的一种快速算法
(苏州华旃航天电器有限公司,江苏苏州 215000)
质量管理几乎贯穿于人类的所有活动,当人们对事物的认识从数量的多少上升到质量的优劣,学会判断和选择“质量更好”的事物时,人类就开启了追求质量甚至创造质量的漫漫长路,可以说人类发展史在某种意义上讲也是一部质量管理的发展史。在实际生产生活中,为了达到更好的质量,人们做了大量的研究和探索,总的来说,在国际上大体的发展脉络可以分为4 个阶段:20 世纪30 年代之前,质量保证以自发检验或专职检验为主;20 世纪30 年代到60 年代开始全面引入“统计质量控制”;20 世纪60 年代到20 世纪末,TQM(全面质量管理)和质量管理体系交映生辉,发展出了直到现在依旧耳熟能详的一系列质量管理手段和方法,例如:ISO 质量体系认证,TS16949(现称为IATF16949),VDA 等汽车产品独有的质量管理体系认证,Six-Sigma(六西格玛)管理,Lean-Six-Sigma(精益六西格玛)管理,QCC 活动等等;在进入21 世纪后,质量管理又从全面质量管理上升到质量哲学时代。随着人们对质量的要求越来越高,质量管控的节点也越来越前移,当发现质量问题时,往往都会对库存产品做风险评估,但是在面对库存品或在制品做质量风险评估这样经典且常见的问题时,却一直没有行之有效的快速算法。
在我国,早在春秋时期就已经有了“物勒工名”的管理制度,从现代质量管理的角度看,“物勒工名”就是追溯制度,以便于管理者检验产品质量,甚至能更进一步追究不良产生时的人员责任。在现代,随着国家的改革开放,经济活动急剧活跃、快速发展,我国的质量管理在吸收大量的国外管理经验的同时,也在结合自身的特点不断的迭代。由于发展速度快,管理水平参差不齐,总的来说现在处于一种“混合”状态:大量的企业在申报ISO9000 系列质量管理体系,也有很多企业在推行全面质量管理,更有优秀的企业在推行自身的质量管理标准;但从另一个角度看,也存在部分企业,在基本的产品质量检验和质量把关上没有清晰的定位,在遇到问题时,没有明确的库存产品质量风险评估方法。从这个角度讲,企业的质量管理就是夹生饭,是一种“混合”的管理。在“混合”管理模式下,出现质量问题时,对库存产品的风险评估更多是靠管理员的经验或者客户的直接要求,全检还是抽样检验,抽样多少是管理员说了算还是客户说了算。
为解决这个问题,我们需要把问题回归到原点—当发现问题时,如何快速的对现有库存或在制品做风险评估。没有交付的质量没有意义,没有质量的交付同样没有意义。只有对库存和在制品快速评估,快速处置,才能争取到宝贵的时间对根因做进一步分析,并加以改善。
1 现行抽样检验方法的历史及其局限性
为了确认产品或服务的各个特性是否合格,测量、检查、测试、量测产品或服务的一种或多种特性,并且与规定要求进行比较的活动称为检验[1]。只有对产品或服务进行检验,才能发现差异,当产品或服务同规定要求的差异超过规定要求的极限时,就称之为不合格。可以说不经过检验,合格或不合格也就无从谈起。
为确认一批产品是否符合规定的要求,最保险的做法是对照规定的要求,对逐一条款的逐一产品进行100%的比对,区分合格品或不合格品。在20 世纪30 年代前,大部分质量工作都是依此进行。但随着经济活动的发展,产品的数量呈几何性上升,数量急剧膨胀,在实际生产中,尤其在出现产品质量异常,需要对库存产品和在制品的质量风险做评估时,100%检验已经难以严格遵循。而评估产品的质量风险又是在实际生产中时常要面对的环节。为了解决这个问题,人们引入了抽样检验的概念—从一批待判断质量是否合格的产品中,基于数理统计的方式随机抽取部分产品进行判断,并以抽取产品的质量情况来代表整体产品的质量状况。由此可见,抽样检验是一种以数理统计为基础的科学的检验方法,是质量监控的最重要、最基础的技术手段。
我国制造业现行的,最广泛采用的抽样方式为GB/T 2828.1-2012《计数抽样检验程序 第一部分:按接收质量限(AQL)检索的逐批检验抽样计划》,以下简称为GB/T 2828.1。此标准为我国参考ISO 2859-1:1999 Sampling procedures for inspection by attributes 制订的,即同等采用。这意味着两者在内容和结构上完全一样。而ISO 2859 的原始标准是参考了美国军标MILSTD-105D:Sampling procedures and tables for inspection by attributes.Version:D 调整型抽样标准。这份标准最初称之为JAN-STD-l05(Joint Army-Navy Standard l05),于1949年设计完成,在1950 年JAN-STD-l05 被修订为MIL-STDl05A。随后在1958 年、1961 年、1963 年和1989 年分别推出了MIL-STD-l05B、MIL-STD-l05C、MIL-STD-l05D 和MILSTD-l05E,特别注意的是E 版本和D 版本基本类似,只是在文字部分加以修订并另行编排。MIL-STD-105D 的民间版于1971年推出,美国国家标准局ANSI 随之将其列入美国国家标准,称之为ANSI/ASQCZ1.4。国际标准化组织于1974 年将ANSI/ASQCZ1.4 稍作修正,并颁布了ISO 2859。美国军方已于1996年用新的美军标MIL-STD-1916 取代MIL-STD-l05E,即MILSTD-l05E 在美军方已经废止。
可以看出,由于此标准在推出时代上有天生的局限性,其采用了接收质量限AQL,并用AQL 来规定样本中的最大不合格品率,这也就意味着接受抽样中的不合格品出现。例如:一批产品的数量为5000 只,假设AQL=0.15%(即良品率为99.85%),按照GB/T 2828.1 的要求,样本量字码为“L”,在“正常抽样一次抽样方案”表中,查询得到结果为:抽样数量=200,Ac=1,Rc=2,这意味着在200 个样品中,发现1 个不良,此批5000 个产品同样认为是合格的。这个抽样方案会带来以下两个问题。
问题1:抽样的200 个样品中,出现一个不良,也可以认为总体5000 个产品满足良率99.85%的质量水平,可是200 个样品中出现一个不良,在不考虑不良品分布的情况下(即假设不良品平均分布在总体中),不良率是不是应该为1/200=0.5%呢?
问题2:在“正常抽样一次抽样方案”表中,样本量字码为“L”,Ac=1,Rc=2,抽样方案同样满足AQL=0.25%(即良品率为99.75%)的要求,那么总体的不良率(或良率)到底是多少呢?
2 抽样的数学模型
为解决这个问题,需要重新看抽样的统计学原理。一般的抽样方法为两种,一种是不放回抽样,即完成每一次对样品的检验后,样品均不放回本体中,下一次抽样永远不会抽到已经检验过的样品,其每一次抽出的样品,每一次检验的结果,均为独立事件,不管是否合格均不会对下一次抽样带来影响;另一种是放回抽样,即完成每一次对样品的抽样后,样品均放回本体中,下一次抽样有可能还会抽到已经检验过的样品[2]。这两种抽样方式,在数学上严格遵从以下两种分布。
2.1 超几何分布
检验后的样品不放回整体母本中,这样整体N中抽样n件产品的组合数为,在所有不良品中,抽样出现k件不良品的组合数为,同样的,抽样n件产品在出现k件不良品后,剩余的应该均为良品,其出现组合数为。
综合以上,可得出发现k件不良的不合格品概率为:
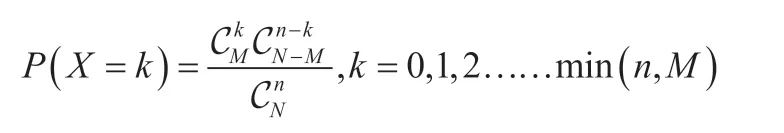
记作X~H(n,M,N)。
其中,当k=0 时,即意味着所有的抽样中没有发现不良品,由此可得[3]:
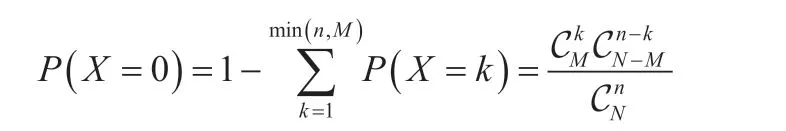
2.2 二项分布
检验后的样品需要放回整体母本中,这样抽样n件产品,出现k次不良的组合数为,由于每次抽样后,产品均放回整体母本中,这样出现k件不良品的概率为pk,同样的,剩余的良品出现的概率为(1-p)n-k。综合以上可以发现k 件不良的不合格品概率为:
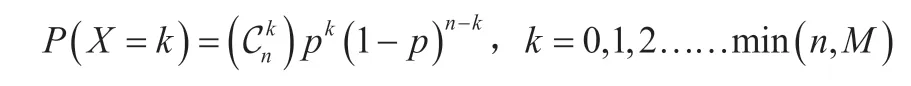
记作X~B(n,p)。
其中,当k=0 时,即意味着所有的抽样中没有发现不良品,由此可得[3]:

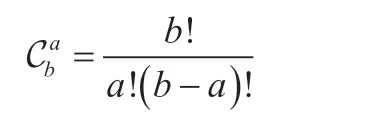
特别的,当a=0 时,=1。
由以上公式可以得出一个重要推论:
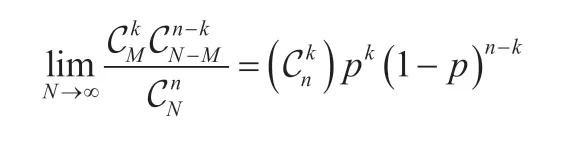
证明如下:
当N无限大时,不良品率,

由于n和k确定,所以:

利用数学我们证明了当N→∞时,超几何分布和二项分布相同;也就是说当总体数量N足够大时,无论是否为放回抽样,在抽样中出现不良品个数的概率是相同的。对于这个结论,我们也可以这样理解,当总体母本数量足够大时,从中抽选几个样品,无论是否放回,抽样出来的样品数量和原始总体母本的数量相比微乎其微,所以其抽样的结果对最终的结果影响也微乎其微了。下文借助Excel 的制表和制图,用两个具体的例子来作说明。
3 超几何分布和二项分布的比较
借助Excel 表格中的超几何分布函数HYPGEOM.DIST和二项分布函数BINOMDIST,可以非常方便的得出数据进行比较,下文只针对固定不良率和固定抽样数量这两种情况,各举一个例子来做示范。
示例一:假设母本N=1000,不良品M=10,不良率=1%,假设抽样中没有发现不良品,不同的样本数量对应的超几何分布和二项分布的数据如表1 所示。
基于这些数据,以抽样数为X 轴,以分布函数的或然率为Y 轴,可以得出如图1 所示的对比图。由图1 可以看出,在此条件下,超几何分布和二项分布的差异不大。
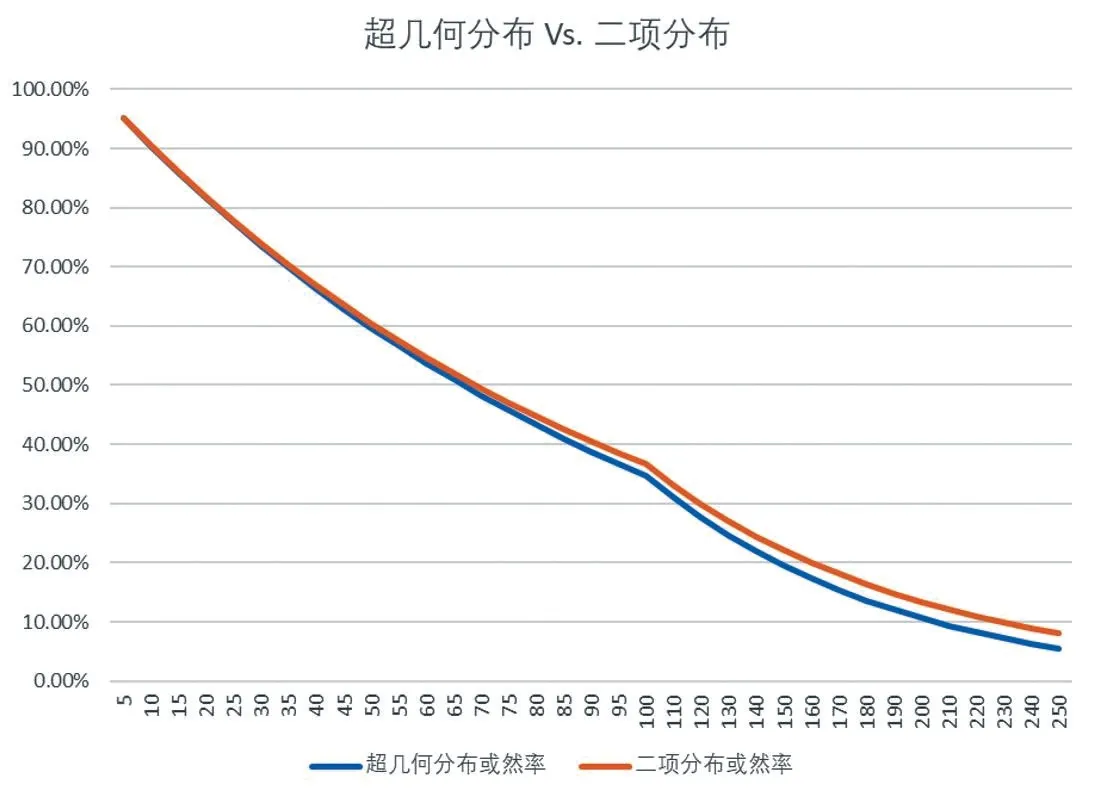
图1 固定不良率下两种概率分布的或然率对比图
示例二:假设母本N=1000,抽样数量为10,假设抽样中没有发现不良品,不同的不良率对应的超几何分布和二项分布的数据如表2 所示。
基于这些数据,以不良率为X 轴,以分布函数的或然率为Y 轴,可以得出如图2 所示的对比图。
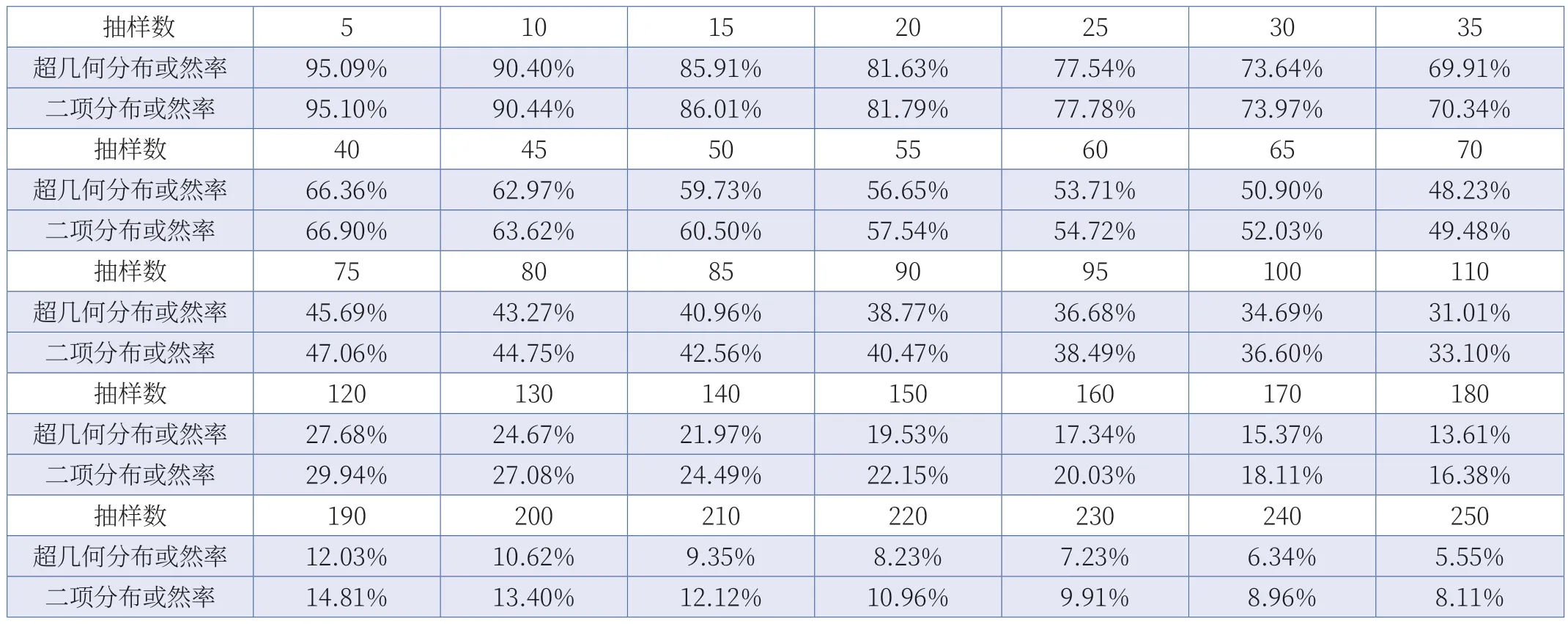
表1 固定不良率下两种概率分布的或然率
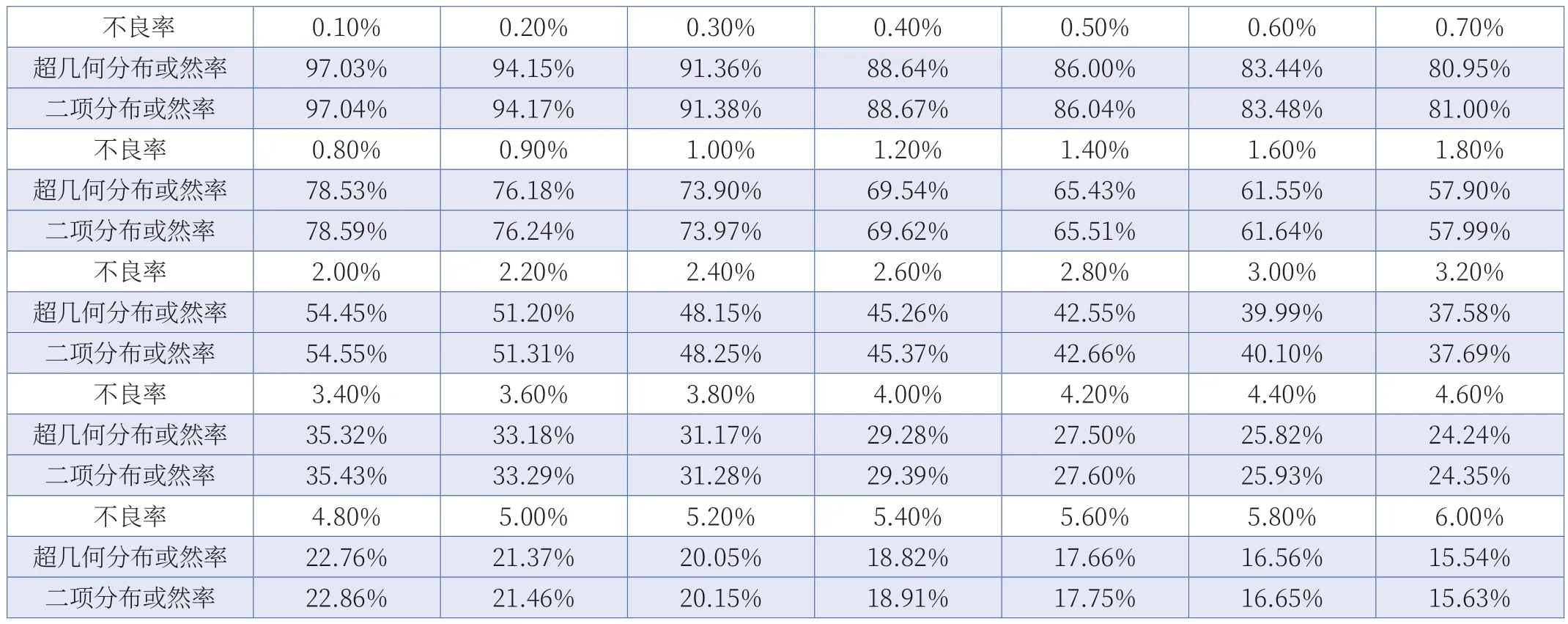
表2 固定抽样数量下两种概率分布的或然率
从上述的实例可以看出,当母本数量N远大于抽样数量M时,超几何分布和二项分布的结果可以视为在工程上无差异。在实际中,一般认为当N>100M 时,超几何分布和二项分布几乎没有差异,在满足这个条件时,一般会使用二项分布来代替超几何分布。
4 快速算法的引出
从二项分布的公式:

可以看出,二项分布在实际计算中,概率密度仅和抽样中的不良数量(或良品数量)、抽样的数量、不良率(或良率)相关,而同总体母本无关,这样就使得我们可以将母本做切分,从而给快速评估母本总体质量水平带来可能。
同时,本文做如下假定:不良品在母本中“均匀”分布。这是因为在日常生产中,库存品的管控一般都是以Lot/批量为基础的,如果不良在一个批次中以随机的形式出现,我们可以认为在同一批次中不良是平均分布的;如果出现特殊情况,我们同样可以用切分的形式,把同一Lot 切分成多个子Lot,从子Lot 的角度看,不良是均布的;或者将相邻的Lot 合拼成一个Lot 组,从Lot 组的角度看,不良品同样是均布的。

图2 固定抽样数量下两种概率分布的或然率对比图
在这样的假定下,结合上文的推导,我们使用二项分布来评估,同时由上文可知:

这意味着,抽样n个产品,出现所有k次不良的概率应为1 减去没有出现不良的概率。
一般的,当我们抽到不良时,无论不良品数量多少,我们都会对整体的质量水平产生疑问。基于此得出我们的结论:在快速计算抽样数量时,抽样方案中出现不良品的概率为:

这个公式说明,在已知不良率的情况下,在抽样中抽到不良品的概率只同不良率和抽样数量相关,同样的这也符合一般的认知:不良率越高,抽到不良品的概率越大;抽样数量越多,抽样的结果越可信。
如果不良率为10%,我们抽样10 个,其结果为多少呢?通过计算可以得出有65.13%的概率可以抽到不良品;如果不良率为1%,我们抽样100 个,其结果为多少呢?通过计算可以得出有63.40%的概率可以抽到不良品。从这两个例子中可以看出,我们能够通过不良率,在比较高的置信率下快速计算出抽样数量,而1-p的本质其实就是良率,在固定良率的基础上,抽样的数量就是良率的抽样次方,也就是一个底小于1 的指数函数。
基于以上分析,如果我们已知不良率为p,那我们的抽样数量N一般可以用以下公式快速得到:,也就是2 到5 倍的不良率的倒数。
我们同样用上边的例子来说明,当不良率为10%时,选α=2,则抽样数量为20,在这个抽样数量下我们抽到不良品的概率为1-(1-10%)20=87.84%。同样,我们也可以计算出当不良率为1%时,选取1%倒数的2 倍,则抽到不良品的概率为86.6%。
已知不良率,用不良率倒数的2 到5 倍作为抽样数,可以在一个比较高的概率下确认库存的不良率是否和已知不良率相同。当发现有不良时,即确认库存中不良情况等于或大于已知的不良率;当没有发现不良时,可以判断库存中不良情况在一个比较高的概率下小于已知的不良率。
5 结束语
在实际生活中,已知产品不良率(或由历史数据得出,或由客户处反馈),利用不良率的倒数的2 到5 倍,快速算出抽样数量,以这个抽样数量对库存做检验,可以有效的确认库存品的不良率是否大于或等于已知的不良率,灵活应用这种算法,合理划分库存品的批次,可以在降低检验成本的同时,有效的对库存的质量风险进行评估。

