基于激光三角法的内径测量不确定度分析
杜华娜,杨铁牛,胡金洲,林浩良
(五邑大学 智能制造学部,广东 江门 529020)
激光位移传感器(Laser displacement sensor,LDS)是非接触式精密测量系统,具有速度快、精度高、适应性强等特点,广泛应用于航空航天、工业自动化等领域[1-2]. 由于LDS 采用的是激光三角法原理,利用光的漫反射进行位移测量,因而在三维曲面测量中存在一定的局限性[3],除系统本身的非线性误差外,其测量精度还受到被测物面物理特性的影响,是激光三角法测量不确定度的主要来源[4-5]. 在微观激光三角测量中,被测物面特征如反射率、表面粗糙度以及划痕和毛孔等是主要影响[6];在宏观激光三角测量中,被测物面几何参数,如倾角、曲率等是主要影响. 激光三角法距离测量的不确定度之一是散斑的影响[7],因为激光散斑使得强度分布的中心位置不再与其几何中心重合;除此之外,表面反射率、光学系统的成像失真、机械振动等都会导致表面测量的不确定度.李兵等[8-9]根据物面倾角建立误差量化模型,分析其对测量精度的影响. Pablo Puerto 等[10]深入探讨激光三角测量系统中最重要的误差源的相关性并对其测量精度进行不确定度分析. 王志超等[11]提出一种基于数显高度尺的LDS 校准方法并进行不确定度评定. 何凯等[12]从LDS 结构、光斑定位及标定方法等角度分析其对测量精度的影响并提出优化方案. 黄潇苹[13]研究了曲面测量过程中影响LDS精度的主要因素,并对实际应用的测量结果进行了模糊不确定度评定. 现有研究主要针对特定机构或测量系统进行误差分析. 本文将从几何光学模型的角度分析激光三角法测量内径不确定度的来源,不考虑高斯光束形状及衍射效应等物理光学模型.
1 激光三角法测量原理
激光位移传感器由半导体激光器、准直透镜、成像透镜、电荷耦合器件(Charge Coupled Device,CCD)以及处理电路等组成. 其基本原理是激光三角法,半导体激光器发射的光束通过准直镜片聚焦到被测物体上,其反射光通过成像透镜投射到CCD 阵列上;信号处理器通过计算投射到阵列上的光点位置得到物体的距离. 图1 所示为直射式激光三角法测量原理图,被测物面上的位移Z和线阵CCD 上激光光斑位置δ的关系为[6]:

其中,θ为被测物面与接收光束的夹角,m为成像透镜的放大倍数.
考虑入射激光光束直径及光强分布,曲率不为零的LDS 内径测量光路如图2 所示. 其中,光斑在曲面上的边界点分别为B、C. 入射光束在被测物面的光斑中心为A,其法线方向为由图2光路可知,在一维位移测量过程中,入射光束的光强在截面方向服从高斯分布,被测物面测量距离的变化ΔZ引起激光光斑在光学传感器上的位置移动Δδ.

图1 激光三角法测量原理
2 内径测量实验
本文拟对某公司挤出机机筒内径(50 ~ 90 mm)的磨损进行检测. 挤出机是塑料成型加工应用最广泛的设备,使用一段时间后,挤出机机筒内壁会出现磨损,而机筒的截面直径关系到配套螺杆的适应性以及生产产品质量的稳定性. 考虑到曲率对测量精度的影响,在发射激光束直径大小不变时,半径越小,则光斑区域内激光束照射在被测物面形成的高度差越大,从而测量误差越大[14];半径越大,测量误差越小;因此,采用30 mm 的内孔零件验证激光三角法应用在机筒测量上的有效性,以确保后续基于激光三角法设计的内径测量仪可用于50 mm 内壁磨损的测量.
2.1 实验平台搭建
基于加工中心搭建如图3 所示的实验测量平台. 将标准的被测零件固定在微动平台上,调整坐标用于校准LDS 实验零点. 其中,S1、S2为基准传感器的激光束方向,用于补偿实验过程中加工中心产生的机械误差.

图3 实验平台
考虑机筒内径空间的限制,本文选用OPTEX 公司的CD22-15-485-M12 激光位移传感器(其详细参数如表1 所示),使用RS485传输信号(优点:信号传输稳定快速,可实现对半径高效率高精度的测量,成本低).

表1 LDS 主要参数表
2.2 示值误差模型
为保证采样的准确性,每次实验需校准传感器安装的高度. 如图4 所示,R为被测物面半径,L0为激光束发射平面,S0为零点位置的LDS 示值,hn为随着X轴方向移动后的理论高度值,kn为测点n所对应的物面斜率. 调节微动平台移动xn,LDS 示值为Sn;则随着物面倾角α变大,测点示值误差 Δhn为:

3 不确定度评定
不确定度作为评定测量系统与测量仪器基本特性的指标,能够衡量计量设备的测量水平,与计量科学技术紧密相关. 测量不确定度的大小可作为表征基准、检定测试和校对测量值溯源的依据,是对测量设备是否满足生产需要的一种评定.
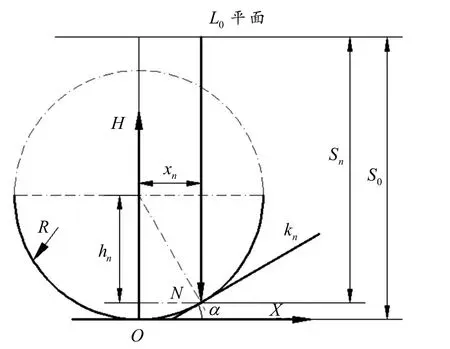
图4 测量原理图
3.1 不确定度来源分析
本方法不确定度的主要来源是系统误差,包括测量仪器本身的定值系统误差以及测量过程中随曲率变化的变值系统误差. 其中,定值系统误差包括被测零件初始零位角误差、LDS 分辨率和线性度等技术指标.
1)阿贝偏角引入的不确定度
被测件与测量轴不共线就会产生阿贝误差[15]. 在内径测量中,LDS 发射的激光束与被测件轴心不在同一直线上时,就会产生误差,该误差可表示为:
式中,σ为待测件相对初始位置倾斜角度变化量,S0为零点位置的LDS 示值.
对内径30 mm、粗糙度1.6 的被测件误差进行阿贝偏角误差分析. 考虑传感器精度在标定基点精度最高,因此实验测点高度定在14 ~16 mm. 根据实验,其在xn= 0.5 mm 时的示值误差为0.001 mm,理论高度Sn= 15.995 mm,则实验平台引入的阿贝偏角为:
故实验平台引入的最大阿贝误差为e1=16 × tan 0.0036°≈0.001 mm . 估计该误差以1μm 为半宽均匀分布,计算可得其不确定度:

2)重复性引入的不确定度
实验过程中,在相同条件下对同一测点重复测量10 次,记录误差;同一实验测点因重复引起的变化不超过1μm,部分数据如表2 所示.

表2 部分实验测点数据 mm
根据贝塞尔公式,可得单次测量的实验标准差为:

其中,n为重复测量次数;xn为间隔0.3 mm 的测点;Yi为测点对应的LDS 示值;为单个测点重复n次的示值平均值. 在实际测量中,每组数据取3 次读数的平均值,因重复性引入的不确定度:

3)实验平台引入的不确定度
实验平台在加工中心的基础上搭建,测量位置的移动依赖加工中心坐标系的校准完成. 如图4所示,LDS 是根据xn的坐标进行测量的,而加工中心反向间隙会对坐标系移动造成一定的行走精度误差,从而影响xn坐标的准确性. 因此搭建了两个基准LDS 用于精度补偿、校准实验测点.

表3 部分内径30 mm 样本的测量数据
由表3 可以看出,在法线倾角小于10°时,对数据进行校正偏移后,误差控制在0.025 mm 以内. 估计该误差以0.0125 mm 为半宽均匀分布,则由实验平台引入的不确定度:

4)测量环境引入的不确定度
偏离标准测量条件时,工件和量具的线性热变形为:

式中,H为物体厚度,mm;α为线性热膨胀系数,被测件材料为钢,厚度10 mm,其热膨胀系数α= 11.5 × 10-6/℃;Δt为温度变化,℃;环境变化主要是室温的变化,在重复N次实验测量过程中,温度变化 Δt<1℃,则:

因此,温度因素对测量的影响误差可忽略不计.
5)光斑定位不确定度
激光的高亮度和准直性便于光束光斑的聚焦及信号的处理,但由于激光的高相干性,在激光光束投射到粗糙的目标面时会形成激光散斑. 谐振腔两端的腔镜对波前的衍射使得激光源发出的光束以高斯光束的形式传播[16],当投射到目标面时,形成的光斑就会呈现出高斯分布. 散斑的存在严重影响了光斑定位的精度,假设光电探测器的精度足够高,则直入射式激光三角位移测量的光斑定位不确定度为:

式中,μ为光斑对成像系统的张角;λ为光源的波长;C为散斑对比度,与照明光源的相干度和被测物面的粗糙度有关,并且满足:

其中,σz为被测表面的粗糙度,lc为光源的相干长度. 当使用激光作为光源时,表面粗糙度远小于激光的相干长度;此时散斑的对比度C近似为1.
实验采用直入射式激光三角测量系统,光源波长655 nm,μ= 17°,由式(12)得到光斑定位不确定度为U4= 0.357 μm.
6)LDS 不确定度
由LDS 的技术指标可知,其测量不确定度主要来源于分辨率和线性度;根据《测量不确定度的表达指南》①ISO/IEC GUIDE 98-3-2008. 测量的不确定性·第3 部分:测量不确定性的表达指南(GUM-1995).,LDS 的分辨率和线性度的分布函数均可以假设为均匀分布. 由表1 技术参数,可知由LDS 分辨率和线性度引入的不确定度分别为:

综上,整个测量系统中各分量引入的标准不确定度及分布函数如表4 所示.

表4 各分量引入的标准不确定度及分布函数
3.2 合成标准不确定度和扩展不确定度
3.2.1 合成标准不确定度
其数学函数表达式为:

由于各不确定度分量之间的相关性可以忽略,则被测量Y的合成方差的数学表达式为:

被测量Y的标准不确定度为:

则合成标准不确定度为:

由表4 可知,不确定度的主要来源是实验平台分量U3,除此之外,整个系统的不确定度为:

3.2.2 扩展不确定度
取置信概率P= 95%,包含因子k= 2,则LDS 测量位移时的扩展不确定度为:U= 2Uc= 0.018 mm.
4 结论
本文采用30 mm 的内径零件分析LDS 应用于内径检测时的不确定度,在物面倾角小于10°时,其不确定度为0.009 mm,满足挤出机机筒内径磨损的测量需求;除可控制的实验平台误差外,整个测量系统引入的不确定度为0.0058 mm,验证了激光三角法测量曲面的可行性,并可广泛应用于大尺寸内径的测量. 本文仅针对LDS 测量内径的可行性展开研究,后续可根据需求设计搭载LDS 的内径测量仪,拓宽激光三角法在曲面测量中的应用.

