基于熵产的离心泵流动损失特性研究
任芸, 朱祖超, 吴登昊, 祝之兵, 李晓俊
(1.浙江工业大学 之江学院,浙江 绍兴 312030;2.浙江理工大学 机械与自动控制学院,浙江 杭州 310018;3.中国计量大学 计量测试工程学院,浙江 杭州 310018)
因其具有单级扬程高、结构紧凑、维护方便,可靠性好等特点,而被广泛应用于石化和航空航天等领域[1]。但离心泵的设计理论至今仍不完善,其在运行过程中会诱发回流漩涡、二次流、动静干涉等不稳定流现象,上述不稳定流对离心泵的性能具有较大的影响,引起离心泵内部大量的能量损失,减少离心泵的水力效率。
在工程实际中,为了达到节能和变换使用流量(扬程)的目的,常存在变转速运行情况,如通过变转速工况调节满足更宽的使用范围[2]。而改变转速后,流道内流速变化较大,且分布不均匀。同时受介质的粘性作用及湍流的无规律脉动特性影响,使得离心泵内部不可避免的存在粘性耗散能的不可逆能量损失。目前,关于离心泵常用的能量损失评估方法主要有4种:1)经验公式[3];2)涡量动力学理论[4];3)能量梯度方法[5-6];4)熵产理论[7-8]。其中,基于泵内水力损失、圆盘摩擦损失和容积损失等能量损失经验公式是以模型泵的外特性为判定依据[9-11],而后3种方法引入了内流分析结果。基于涡动力学的方法通过对泵内局部不良流动放大,研究其与水力性能的关系达到优化水力设计的目的[12-14]。能量梯度方法对计算的流场数据进行处理,获得流道内能量梯度函数分布,并基于能量梯度理论对泵内失稳进行分析[15]。熵产作为一种直观反映流体内部不可逆损失发生位置及能耗空间分布的有效工具,为离心泵性能改进及指导其水力优化提供了新的方法Li等[16]、Hou等[17-18]基于熵产理论分析了离心泵内能量损失情况及其产生的主要原因。同时,熵产理论也被广泛应用于风机内部的能量损失分析[19]、侧流道泵的内部流动损失研究[20]、低温潜液泵空化诱导流动损失研究[21]、自吸泵内部能量损失分析[22]和水轮机内流损失研究[23]。上述研究中均强调了熵产方法分析泵内流动损失比较直观且可以得到泵内流动损失的细节信息。
本文首先针对一航空航天领域应用普遍且对偏小流量下的性能要求较高的诱导轮离心泵模型进行变转速试验,然后基于熵产理论并结合数值计算结果,分析随着转速的不断变化,离心泵内部各个部件的能量损失分布规律,揭示转速对离心泵性能特性的影响规律。
1 离心泵的模型建立
1.1 熵产理论
整个系统计算域内的总熵产Spro为直接耗散熵产Spro,D、湍流耗散熵产Spro,D′和壁面熵产Spro,W之和,其计算公式为:
Spro=Spro,D+Spro,D′+Spro,W
(1)
式中Spro,D和Spro,D′定义为:
(2)
(3)
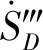
(4)
式中:α=0.09;ω是比耗散率;k是湍流强度。
由于熵产率存在较强的壁面效应,且时均项较为明显,其壁面附近熵产计算的公式为[8]:
(5)
式中τ是壁面切应力,Pa;S是面积,m2;v是近壁面速度,m/s。
1.2 实验模型与数值计算
1.2.1 实验模型
本文以带诱导轮的离心泵为研究对象,为便于开展相关实验研究,除了诱导轮采用不锈钢制造外,试验泵其他部分均采用有机玻璃制造,其几何参数为叶轮进口直径D1=88 mm,出口直径D2=148 mm,叶轮出口宽度b2=8.5 mm,蜗壳基圆直径D3=154 mm,蜗壳出口直径D4=40 mm。
由于有机玻璃材料强度的限制,模型泵的最高设计转速为3 600 r/min,该转速下对应的电机功率为7.5 kW,电机转速通过ABB变频器进行调节,实验转速分别设为3 600、2 600和1 600 r/min。基于相似定理,不同转速对应的设计流量和扬程分别为(Qd=18.8 m3/h,Hd=48 m)、(Qd=13.6 m3/h,Hd=25 m)和(Qd=8.37 m3/h,Hd=9.5 m),实验用模型泵具体结构如图1所示。

图1 实验用泵结构Fig.1 Main structure of pump model
1.2.2 数值计算
本文采用六面体结构化网格对全流道进行网格划分。图2为计算域网格。离心泵进口采用总压进口条件,出口给定出口质量流量条件,通过控制模型的质量流量来控制流体速度的大小,同时假定进口截面上的压力均匀分布。计算的流体介质为水,介质温度设为298 K。近壁面处选择可伸缩壁面函数对近壁区进行处理,计算中忽略表面粗糙度对流场的影响。
本文在ANSYS CFX的平台上对n=3 600 r/min的泵模型选用SSTk-ω湍流模型进行了网格无关性分析。表1为6组不同数量网格模型在设计工况下的计算结果,可以看出,当网格数大于400万以后,随着网格数的增加,扬程的波动较小,因此,本文在网格4的基础上进行后续的研究。

图2 计算域网格模型Fig.2 Mesh of computational domains
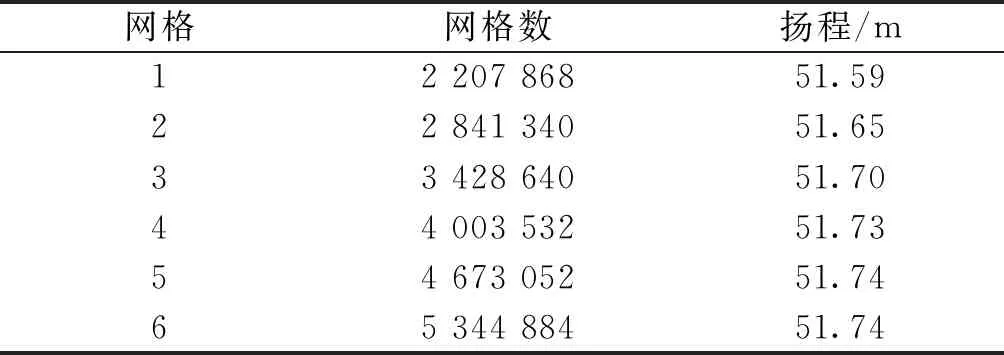
表1 网格无关性分析结果(1.0Qd)Table 1 Mesh independency analysis (1.0Qd)
2 结果与分析
2.1 外特性对比分析
通过分析实验结果,得到不同转速下离心泵外特性曲线,如图3所示。
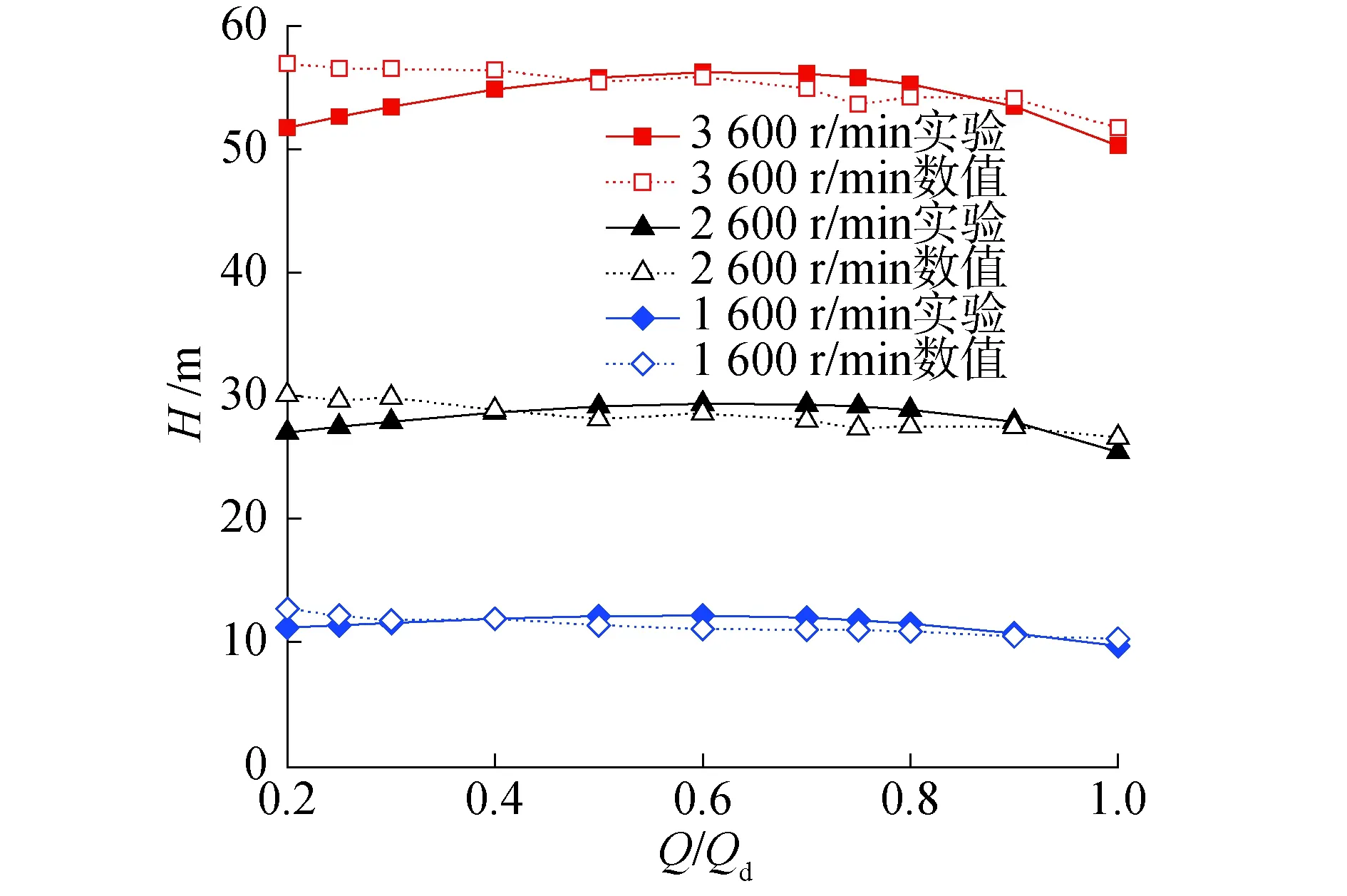
图3 不同转速下模型泵Q-H曲线Fig.3 Q-H curves of pump model under different speeds
从图3可以看出,在试验条件下该离心泵不同转速下的Q-H曲线在小流量工况均存在明显驼峰现象。以3 600 r/min为例,在设计工况下的实验扬程为50.3 m,数值计算的扬程为51.7 m,相对误差约为3%;在小于0.3Qd下的个别流量工况,数值计算的相对扬程误差超过5%,除此之外,计算值与实验值基本趋于一致。
2.2 不同转速下泵内流动损失分布特征
图4为模型泵小流量至设计流量区域内不同转速对应的局部熵产和壁面熵产分布规律,从图中可以得出:泵内局部熵产和壁面熵产值随着转速的增大而增大;在对应的转速下,直接耗散熵产Spro,D和湍流耗散熵产Spro,D′随流量的增加呈现先减小后增大的趋势,而壁面熵产Spro,W随流量的增加呈现逐渐增大的趋势。对比3种不同类型的熵产,其中壁面熵产Spro,W所占的比率最高,湍流耗散熵产Spro,D′次之,直接耗散熵产Spro,D最小;随着转速的减小,壁面熵产所占比率基本呈现逐渐增大的趋势,而湍流耗散熵产和直接耗散熵产则呈现逐渐减小的趋势;其中在3 600 r/min下,0.2Qd的壁面熵产值为2.5 W/K,所占比率为37%,1.0Qd的壁面熵产为3.07 W/K,所占比率为48%。而转速降低到1 600 r/min时,0.2Qd和1.0Qd下的壁面熵产值降低至0.42 W/K和0.47 W/K,而其所占比率上升至48%和54%。因此,对于离心泵,壁面熵产是泵内能量损失的主要来源,其值不可忽略。
图5为模型泵总熵产和不同区域所对应的熵产值,其中Spro,total代表总熵产值,Spro,imp代表叶轮内的熵产值,Spro,vol代表蜗壳内的熵产值,Spro,ind代表诱导轮内的熵产值,Spro,cav代表腔体内的熵产值,Spro,wr代表口环间隙内的熵产值。通过分析该泵总熵产值和不同区域内的熵产分布情况,可以得到:1)总熵产值随着转速的降低而逐渐减小;3种转速下,总熵产值均在0.6Qd下达到最小,其值分别是5.65、2.38和0.81 W/K;不同转速下的对应流量工况的总熵产比值与转速比值大致呈2.5倍的函数关系。2)腔体内部的熵产值最大,在3 600 r/min其所占比率最高可以达到38%,在1 600 r/min其所占比率最高可以达到58%;蜗壳内部的熵产值略小于腔体,在3 600 r/min和1 600 r/min所对应的最高比率分别为32%和25%;其后分别是叶轮和诱导轮,口环间隙的熵产值最小,其比率大致为1%~2%,基本不受转速和流量工况的影响。3)相比高转速,1 600 r/min下的叶轮和诱导轮的熵产所占比率下降明显,其原因在于转速的降低使叶轮和诱导轮内部的流动变得相对比较稳定,其对应的湍流耗散损失显著下降。
2.3 不同转速下泵内部流动特征
为了进一步分析离心泵内部流动损失的具体位置和流动损失的诱导原因,以各转速下的设计工况(1.0Qd)作为分析对象,开展内部流动特征分析。
图6为不同转速下设计工况叶轮内局部熵产和涡核分布特征,叶轮内的漩涡以Q准则表示[24],Q准则取值为6×104s-2。从图中可以得出:1)随着转速的降低,叶轮与蜗壳内部的局部熵产值(EPR)和叶轮流道内的分离涡的强度显著下降。叶轮内部的损失主要集中在叶轮进口处和叶轮出口处,其主要原因是当水流进入叶轮后,首先对叶轮叶片进口端产生冲击,且随着转速的增加水流流速也随之增加,从而加剧了水流冲击,造成较大的冲击损失。同时,叶轮与蜗壳及隔舌的动静干涉效应引起了叶轮出口处、蜗壳内部以及隔舌附近的能量损失,转速增加的同时也加剧了动静干涉效应,从而加剧了叶轮、蜗壳以及隔舌附近的能量损失;2)结合叶轮内部速度流线图可以看出,叶轮内部存在大量的涡流,这种漩涡流动导致了叶轮内部存在大面积的涡核,叶轮内部的分离流动和叶轮出口的回流是导致涡核产生的直接原因。这种不稳定涡流会引起较大的能量损失,随着转速的增加,叶轮内部的涡流强度和涡核分布面积得到显著增强,使得叶轮内部能量损失明显增加;3)从叶轮内部的流线图可以发现不稳定漩涡均出现在长叶片的工作面与短叶片的背面之间,而在短叶片的工作面与长叶片背面则流动相对比较稳定。这说明叶轮内部的流动分离易在长叶片的工作面发生,从而在长叶片与短叶片的流道中间形成明显的低速涡区,进而导致能量损失。
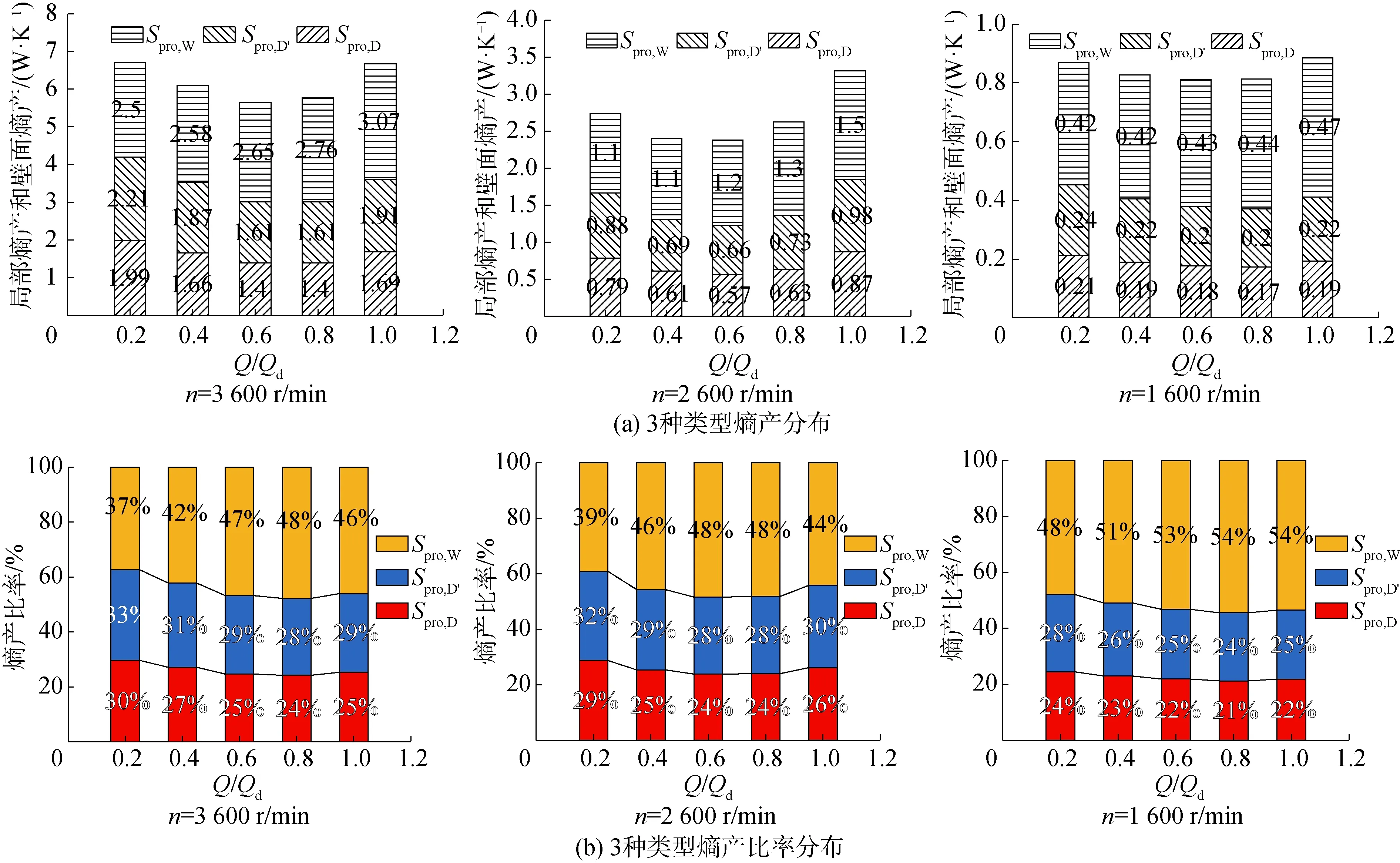
图4 不同转速和流量下模型泵3种类型熵产分布特征Fig.4 Entropy production rates of pump model under different speeds and flow rates
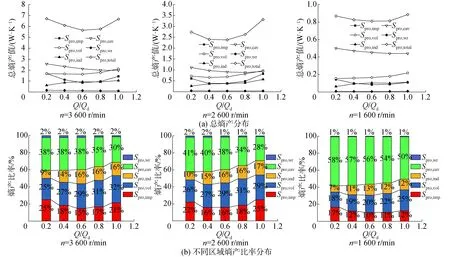
图5 不同转速和流量下模型泵总熵产分布特征Fig.5 Total entropy production rate of pump model under different speeds and flow rates
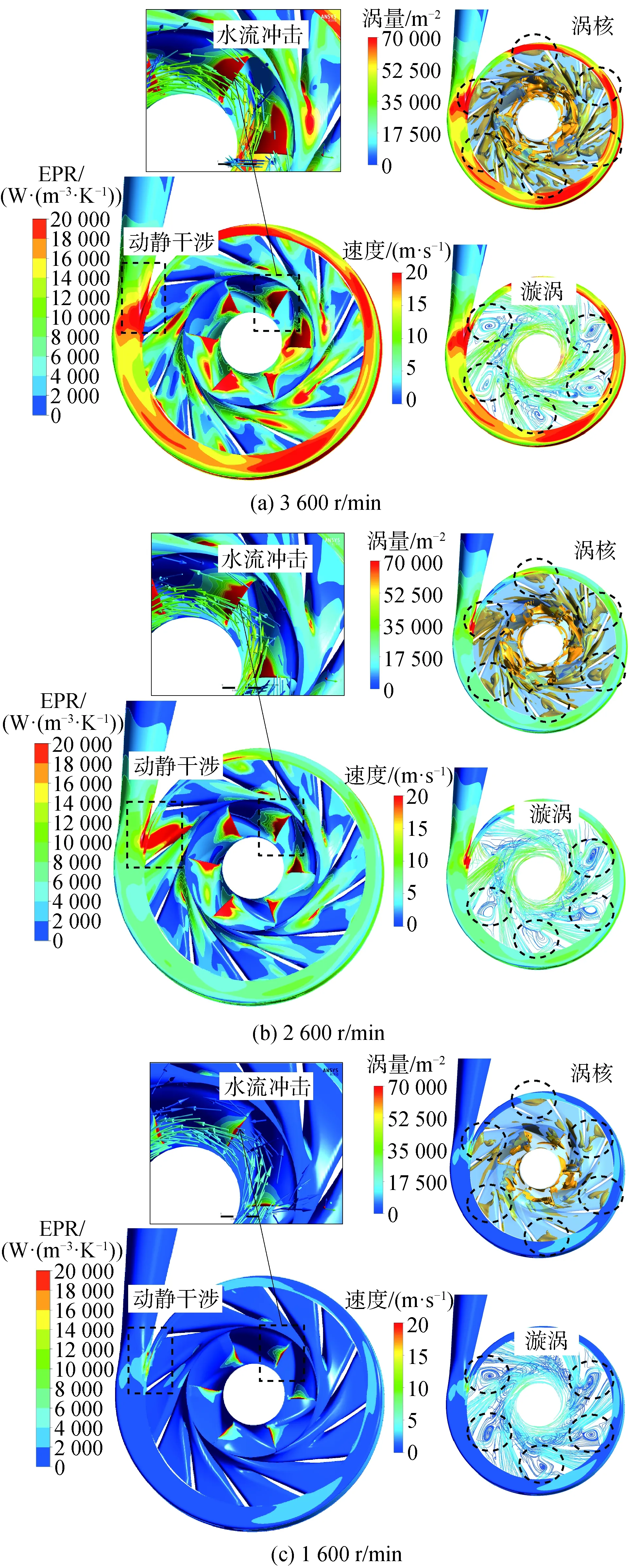
图6 设计工况下离心泵内局部熵产和涡核分布特征Fig.6 Local EPRs and vortex cores of centrifugal pump under design flow rate
2.4 不同转速下诱导轮内部流动特征
图7为不同转速下设计工况对应的诱导轮局部熵产和涡核分布特征,诱导轮的泄漏涡以Q准则表示,Q准则取值为Q=5×105s-2。

图7 不同转速下设计工况对应的诱导轮内局部熵产和涡核分布特征Fig.7 Local EPRs and vortex cores of inducer under design flow rate
从图7中可以得出:随着转速的降低,诱导轮的局部熵产值和叶顶间隙泄漏涡的强度显著下降。诱导轮内部的损失主要集中在叶顶处,其主要原因是在于叶顶泄漏涡的影响,泄漏涡引起叶顶处出现与主流方向相反的液流,该反向液流与主流液体发生干扰,严重影响诱导轮内部流态;泄漏涡导致流态恶化,降低诱导轮的做功能力和加剧叶顶处的能量损失,具体如图8所示。图8中进一步揭示了诱导轮内部的涡量分布主要集中在叶顶处和靠近叶轮进口的区域,靠近叶轮进口区域的涡量主要由叶轮进口出现局部回流导致的,这也使得该区域的涡核和能量损失显著增加。

图8 设计工况诱导轮叶顶间隙涡量分布特征(3 600 r/min)Fig.8 Vortex distribution of inducer tip under design flow rate (3 600 r/min)
3 结论
1)离心泵内局部熵产和壁面熵产值随着转速的增大而增大;同一转速下,直接耗散熵产和湍流耗散熵产随流量的增加呈现先减小后增大的趋势,而壁面熵产随流量的增加呈现逐渐增大的趋势。壁面熵产所占的比率最高,湍流耗散熵产次之,直接耗散熵产最小。
2)腔体、蜗壳和叶轮是离心泵内能量损失的主要区域,口环间隙的熵产值最小;不同转速下的对应流量工况的总熵产比值与转速比值大致呈2.5倍的函数关系;低转速的叶轮和诱导轮的熵产所占比率显著下降,其原因在于转速的降低使得叶轮和诱导轮内部的流动变得相对比较稳定,其对应的湍流耗散损失显著下降。
3)随着转速的降低,叶轮与蜗壳内部的局部熵产值和叶轮流道内的分离涡的强度显著下降。叶轮内部的损失主要集中在叶轮进口处和叶轮出口处,其主要原因在于叶轮进口的流动冲击和叶轮出口的动静干涉效应。叶轮内部的分离流动和叶轮出口的回流是导致涡核产生的直接原因,随着转速的增加,叶轮内部的涡流强度和涡核分布面积显著增强。诱导轮内部的损失主要集中在叶顶处,其主要原因是在于叶顶泄漏涡的影响。

