基于多信息数据融合滤波的坡度识别算法

付 翔， 何宗权， 黄 斌， 裴 彪， 杨凤举

(1. 武汉理工大学 汽车工程学院， 湖北 武汉 430070； 2. 武汉理工大学 现代汽车零部件技术湖北省重点实验室， 湖北 武汉 430070； 3. 武汉理工大学 汽车零部件技术湖北省协同创新中心， 湖北 武汉 430070； 4. 武汉理工大学 湖北省新能源与智能网联车工程技术研究中心， 湖北 武汉 430070)

纵向坡度是汽车底盘电控的重要路况信息和控制输入参数，对车辆动力性、安全性、舒适性和燃油经济性十分重要.随着车辆智能化、无人化的深入推进，车辆动力学控制的准确性和实时性要求不断提高，道路纵向坡度信息获取的准确度和鲁棒性需求明显增强.例如，在高级驾驶辅助系统中，道路坡度和车轮的垂向力可用于预测车辆侧翻情况，用于系统及时发出警告，甚至为了避免事故，对车辆采取及时有效的稳定性控制.因此，纵向坡度信息作为车辆底盘动力学控制的关键参数，是当前研究的热点.

针对纵向坡度的识别，主要有基于车辆动力学模型、基于加速度传感信息、基于GPS的方法.基于车辆动力学模型的识别方法较多依靠模型参数的准确性，其扰动多为高频噪声.基于加速度传感信息的识别方法容易受到传感器信号质量的影响，容易导致信噪比低的问题，其干扰主要为低频噪声.因此，为了增强在复杂噪声干扰下的坡度识别效果，目前的研究热点是采用数据融合估计方法实现坡度识别.R. WRAGGE-MORLEY等[1]采用自适应非线性观测器，实现了基于车辆动力学模型的道路坡度识别.雍文亮等[2]建立了定坡度和定坡度变化率两种道路模型，利用车辆纵向动力学和加速度传感器量测值，采用多传感器信息融合滤波算法获得准确的坡度估计值；但是由于利用了传统燃油车上多传感器信息，如发动机转矩信号、轮速信号，其动力传递路线长，导致车轮受力相对于发动机端的动力输入存在一定迟滞；且受限于传感器采样频率，信号延迟时间不同，因此需要对输入信号进行时间同步处理，这会影响车辆状态参数获取的时间一致性.R.A.CORDEIRO等[3]使用二阶非线性拓展卡尔曼滤波器进行了路面坡度和轮胎-地面附着力的联合估计，采用实车数据离线仿真的方式证明了算法有效性.S. KIM等[4]利用车载加速度计信号并结合卡尔曼滤波算法对坡度信息进行了实时识别.现有大多数研究在假设缓变的坡度基础上，提出定坡度、零坡度变化率的数学模型，鉴于实际道路坡度具有不确定性和随机性，忽略坡度的变化不仅不符合实际坡度特征还会导致坡度识别算法收敛速度缓慢[5].林楠等[6]针对目前大多数研究完全忽略道路坡度变化率特征造成时间延迟的问题，运用纵向加速度传感器数据表达了道路坡度的变化率信息，构建了坡度估计卡尔曼滤波器；其试验结果表明，考虑道路坡度变化率能有效降低道路坡度在线估计的延迟时间.

基于GPS的坡度识别方法主要通过提取导航坐标下纵向和垂向运动参数进而推导坡度值.K. JO等[7]基于GPS信息和车载传感器数据的融合处理，根据道路坡度的数学模型设计了坡度估计器.基于GPS和车载传感器的坡度识别方法需要高精度GPS作为硬件支撑，提高了传感器成本；GPS信号受到遮挡、干扰产生信号中断和失真时将会对坡度识别精度和实时性产生极大影响.

文中针对分布式驱动车辆在大坡度、大坡度变化率下的坡度识别问题，利用轮毂电动机动力参数可以直接从高速CAN上快速、准确获取的能力，以提高车轮动力学参数获取的精度.在考虑坡度变化率特征信息的基础上，采用车辆动力学坡度法、加速度传感信息坡度法、GPS识别法融合识别的方式，设计交互多模型卡尔曼滤波(interactive multi-model Kalman filter，IMM-KF)算法.通过dSPACE仿真平台验证在定坡度、连续变化坡度、驻坡工况下算法的有效性.

1 道路坡度识别模型的建立

1.1 基于车辆动力学模型的坡度量测值计算

车辆纵向动力学模型如图1所示.

图1 车辆纵向动力学模型

一般道路坡度较小，忽略滚动阻力，整车纵向动力学方程可近似表示为

(1)

式中：m为车辆质量；vx为纵向车速.车轮旋转动力学方程为

(2)

式中：Fx为各轮胎纵向力之和；下标j=1，2，3，4分别代表左前轮、右前轮、左后轮、右后轮；ωj为旋转角速度；Jwj为绕轮心的转动惯量；Tdj为驱动力矩；Tbj为制动力矩；Fxj为与地面之间的纵向力；f为轮胎的滚动阻力系数；i=tanθ,θ为坡度角，i为坡度值；Rt j为车轮滚动半径；Fzj为垂向力.

考虑车辆因纵、侧向加速度引起的轮荷转移，各车轮垂向力表达式为

(3)

(4)

式中：g为重力加速度；hg为车辆质心高度；L为前后轴距，L=a+b.

1.2 基于加速度传感信息的坡度量测值计算

从运动学方法考虑，车载加速度传感器测量值受到车辆自身纵向行驶加速度以及路面坡度的综合影响，则加速度传感信息表达式为

(5)

(6)

一般情况下，坡度作为缓变值，忽略坡度变化率信息可以为计算带来便利.但是对于较为剧烈的坡度变化工况，忽略坡度变化率会使得坡度识别响应缓慢，难以达到期望的实时性、快速性要求，因此，在基于加速度传感器观测的基础上，引入了坡度变化率信息，对式(5)做微分运算，可得

(7)

可变形得

(8)

1.3 基于GPS的坡度量测值计算

基于GPS的坡度识别方法通过提取导航坐标下纵向和垂向运动参数推导坡度值，采用GPS的速度信息v和高程信息h计算单位行进步长过程中的高程差Δh和水平位移差Δs[8]，则坡度计算式为

(9)

其中

Δs=vΔt，

(10)

Δh=hk-hk-1,

(11)

式中:hk为k时刻高程.

2 坡度识别算法

2.1 坡度识别算法架构

在车辆行驶过程中，基于动力学的坡度识别效果严重依赖于车辆模型精度，通常受高频噪声影响较大；基于加速度传感信息的坡度识别方法受加速度传感器静态偏差影响较大，通常属于低频噪声干扰；而GPS受到天气因素影响且采样频率较低，实时数据更新相对较慢，该方法受到GPS精度、更新频率制约.3种坡度识别方法的效果受到多种不同类型因素的制约，但是都有其应用的优势，因此考虑多模型混合输入的联合估计可以增强高低频段噪声下的抗干扰性、减弱环境因素对传感信息的扰动、削弱动力学模型精度对结果的影响权重，从而得到鲁棒性好、准确度高的坡度识别结果.

基于上述考虑，引入了交互式多模型(interactive multi-model，IMM)算法，同时采用卡尔曼滤波算法[9].卡尔曼滤波器的加权平均融合方法无法根据测量值优劣自适应地倚重更有利的测量信息[10]，而IMM算法可以实现不同模型的权重切换以自适应实时车辆状态，自动降低不同运行环境下的误差因素干扰，进而选取最优估计模型.因此结合卡尔曼滤波算法和IMM算法构建自适应模型权重切换算法有利于提高坡度估计精度.IMM-KF算法结构如图2所示，IMM-KF算法主要包含多个滤波器、模型概率估计、交互作用器、状态估计融合.

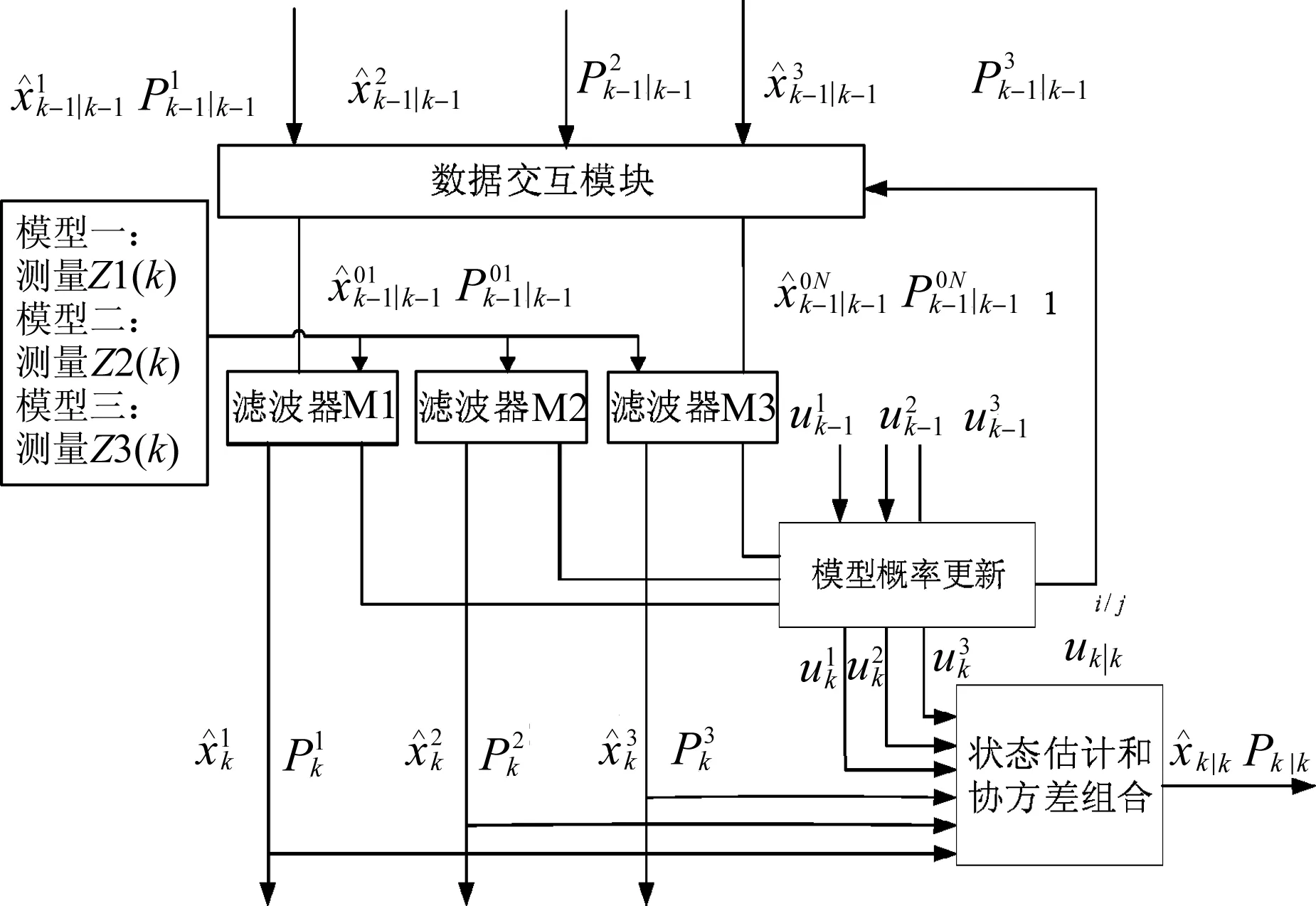
图2 IMM-KF交互多模型算法总体架构

假设系统第j个模型的状态方程为

Xj(k+1)=Φj(k)Xj(k)+Gj(k)Wj(k)，

(12)

Z(k)=H(k)X(k)+V(k).

(13)

IMM-KF算法是以迭代方式进行的，每次递推主要分为以下4个步骤：

1) 输入交互.

模型j的预测概率(量纲一化常数)为

(14)

式中：μi(k-1)为模型i在k-1时刻的概率.模型i到j的混合概率为

(15)

模型j的混合状态估计为

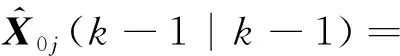
(16)

模型j的混合协方差估计为

(17)

式中：pij为模型i到j的转移概率.

2) 卡尔曼滤波(模型j).

下一状态预测为

预测误差协方差为

(19)

卡尔曼增益矩阵计算式为

Kj(k)=Pj(k|k-1)HT[HPj(k|k-1)HT+R]-1，

(20)

滤波更新后状态为

(21)

滤波协方差计算式为

Pj(k|k)=[I-Kj(k)H(k)]Pj(k|k-1).

(22)

3) 模型概率更新.

采用似然函数更新模型概率μj(k)，模型j的似然函数为

(23)

(24)

4) 输出交互.

基于模型概率，对每个滤波器的估计结果加权合并，得到总的状态估计为

(25)

总的协方差估计为

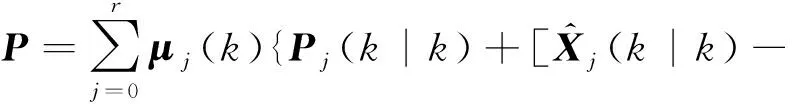
(26)

2.2 多数据融合滤波坡度识别算法

根据离散状态方程式，建立基于车辆动力学的定坡度模型(模型一).观测器的状态方程为

(27)

模型的观测量是加速度传感器采集的加速度信息，可得量测方程为

(28)

建立基于加速度传感信息的坡度变化模型(模型二)，观测器的状态方程为

(29)

模型的观测量是加速度传感器采集的加速度信息，可得量测方程为

(30)

建立基于GPS的坡度模型(模型三)，观测器的状态方程为

(31)

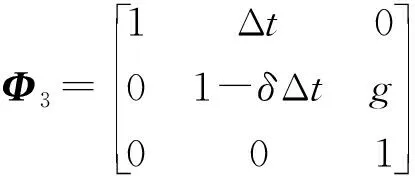
模型的观测量是加速度传感器采集的加速度信息，可得量测方程为

(32)

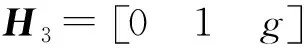
3 仿真验证

3.1 车辆参数及试验仿真平台

图3为 DSPACE仿真平台和测试方案流程图.

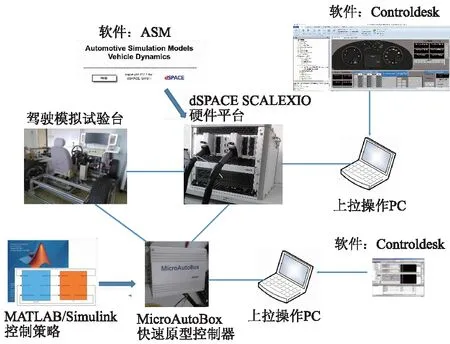
图3 DSPACE仿真平台和测试方案流程图

文中所采用的车辆参数如下：整车质量为4 000 kg；轴距为3.56 m；质心到前轴的距离为2 m；风阻系数为0.62；迎风面积为3.2 m2；车轮半径为0.475 m；电动机额定功率为35 kW；电动机额定转速为1 000 r·min-1；电动机额定转矩为350 N·m.

文中以dSPACE公司的硬件平台MicroAutoBox和SCALEXIO作为实时仿真平台，实时运行基于ASM动力学模型建立的道路交通环境和四轮独立驱动电动汽车动力学模型.以dSPACE公司的MicroAutoBox 作为快速原型控制器，实时运行基于MATLAB/Simulink 的坡度识别算法.

3.2 硬件在环仿真试验

3.2.1 定坡度爬坡试验

在路面条件较好的行驶工况下，坡度的路面较为平整且变化率平稳，常表现为类似定坡度的良好路面，因此为了模拟常规运行工况，设置了定坡度路面.仿真开始时，车辆位于坡道前的平地上，由静止加速至预定速度后，开始爬坡试验，车辆爬上坡道后，停在坡顶的平地上.考虑所用分布式驱动越野车的常用行驶工况和运行特点，设置了10%、20%、30%、40%、50%、60%的大坡度仿真试验，以证明在复杂极限工况下所用算法的性能.图4为定坡度工况、不同坡度下所用算法的坡度识别结果.

图4 定坡度工况、不同坡度下坡度识别结果

由图4可见，识别坡度与实际坡度的曲线趋势走向基本吻合，证明了所用算法的良好跟随效果.在坡度过渡路面，所用算法出现了不同程度的震荡和轻度滞后，尤其是随着坡度变化率的增加，坡度识别结果出现的震荡趋势更明显，分析认为强烈的坡度变化，一方面导致车辆运动状态受到瞬时扰动，加速度计的高频信号震荡严重，另一方面为多自由度簧上质量受悬架弹簧和减震器的阻尼作用，簧上质量出现了震荡式波动，造成原始测量信号噪声和系统噪声过大，但是从结果看，所用算法的识别结果在较短时间得以快速收敛，直至基本消除误差，证明了算法拥有良好的准确性和鲁棒性.

3.2.2 连续变化坡度试验

为了提高车辆在坡度连续变化路段的坡度快速识别响应能力，所提出的IMM-KF算法考虑了坡度变化率信息，因此，设置了连续变化坡度工况，以验证在坡度变化路段所提出算法的有效性.图5为坡度连续变化工况坡度识别结果.

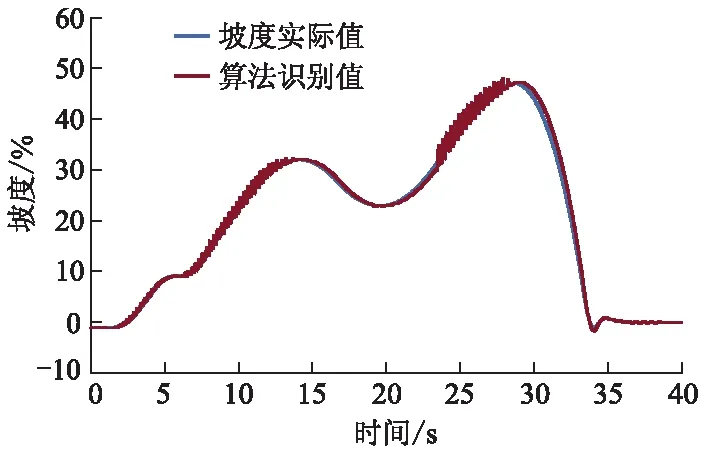
图5 坡度连续变化工况坡度识别结果

由图5可见，在连续变化坡度试验工况下，所提出的IMM-KF算法识别结果具有快速跟随实际坡度的能力，证明将坡度作为变化量，即考虑坡度变化率信息，能够提升坡度识别的快速性.由于仿真试验坡度模型模拟了越野工况下的坡度工况，试验坡度值及其变化率较大时，所用算法出现了一定小幅波动，波动误差值为±3.1%，处于合理误差范围内.仿真结果显示，所提出的坡度识别算法拥有良好的稳定性和准确性，具备快速识别坡度的能力.

3.2.3 坡道驻车试验

为了验证所用算法在车辆驻车时的可用性，以拓展所用算法的应用工况，进行了坡道驻车试验.图6为坡度起步工况坡度识别结果.

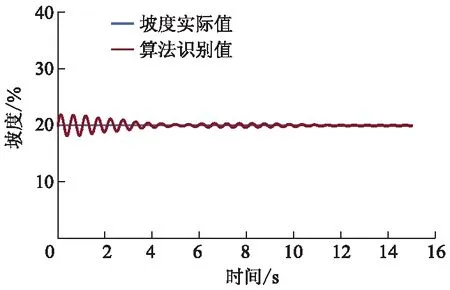
图6 坡度起步工况坡度识别结果

车辆初始位于20%的坡度上，车速在PID车速控制器作用下始终保持为0左右.由图6可见，在初始阶段，识别结果出现了一定震荡，坡度识别峰值为21.78%，峰值识别误差率为8.9%；误差原因应为车辆处于非完全静止状态，主要受PID车速控制器初始阶段的超调震荡影响，而且GPS量测值无法充分有效利用，较多依靠车辆纵向动力学模型识别坡度，导致结果出现一定的震荡波动.经历短时间小幅波动后，坡度识别结果逐渐收敛至稳态坡度实际值，最终的坡度识别结果较好地跟随实际坡度值，超调震荡小，收敛快速，效果良好.

4 结 论

1) 通过建立动力学模型、加速度传感模型和GPS识别模型，引入坡度变化率信息，基于多传感器信息融合滤波原理应用交互式多模型滤波算法(IMM-KF)，为坡度识别提供了技术支持.

2) 通过DSPACE硬件在环平台仿真测试，在定坡度爬坡工况下，随着坡度及其变化率的增加，识别结果在坡度剧烈变化初期出现一定超调，但随后得以快速抑制，能够准确识别坡度值.在连续变化坡度工况下，识别结果超调震荡小，波动误差值为±3.1%，能够良好跟随实际坡度值.在20%坡道驻坡工况下，峰值识别误差率为8.9%，震荡主要出现在识别初期，随后识别结果逐渐收敛至实际值.表明了所提出的IMM-KF坡度识别算法在各种坡度类型和驻坡工况下具有良好的坡度识别效果，证明了分布式驱动车辆坡度识别算法的准确性和鲁棒性.