光学遥感卫星平面定位精度误差分析

满益云 江志军

光学遥感卫星平面定位精度误差分析

满益云 江志军

（钱学森空间技术实验室，北京 100094）

高分辨率光学遥感敏捷成像卫星，在无地面控制点条件下，要达到米级的平面定位精度，需进行卫星系统全链路的误差分析，对系统误差进行高精度标定，对随机误差进行有效抑制。通常光学遥感卫星的几何定位分为物理几何模型和通用几何模型，物理几何模型基于共线方程，使用光学遥感器内方位元素和卫星平台姿轨外方位元素共同建立遥感图像的精确几何定位模型，其中光程差和大气折射等环境影响要素不可忽略，需要通过建模消除其偏移量。文章通过物理几何模型和通用几何模型的转换，利用WorldView-2卫星数据和参数进行了精度交叉验证，结果表明经过光程差和大气折射偏移校正之后，计算分析得到的平面精度与公布的无控制点精度优于5m（90%概率圆误差）的结果基本一致，说明了误差分析方法的正确性。

光学遥感卫星 误差分析 平面定位精度 敏捷成像 无控制点

0 引言

近年来，随着光学遥感卫星分辨率的提高，尤其是商业光学遥感卫星的快速发展，美国等国家的高精度卫星得益于先进的系统优化设计、高分辨率的遥感器、高精度定姿与定轨、高效率地面处理等技术，无地面控制点几何定位精度达到了优于3m@CE90（90%概率圆误差，本文中无特殊说明，平面定位精度均采用@CE90来表征）的水平（如图1所示），已经具有优于1∶5000全球范围大比例尺地图的测绘能力。定位精度的提高，将显著提升卫星系统的应用效能。如何实现无控制点米级定位精度，需要进行卫星系统全链路的误差分析，并对重点环节和要素采取有效的措施加以控制。对存在的系统误差进行高精度标定和校正，对存在的随机误差进行有效的抑制[1-5]。

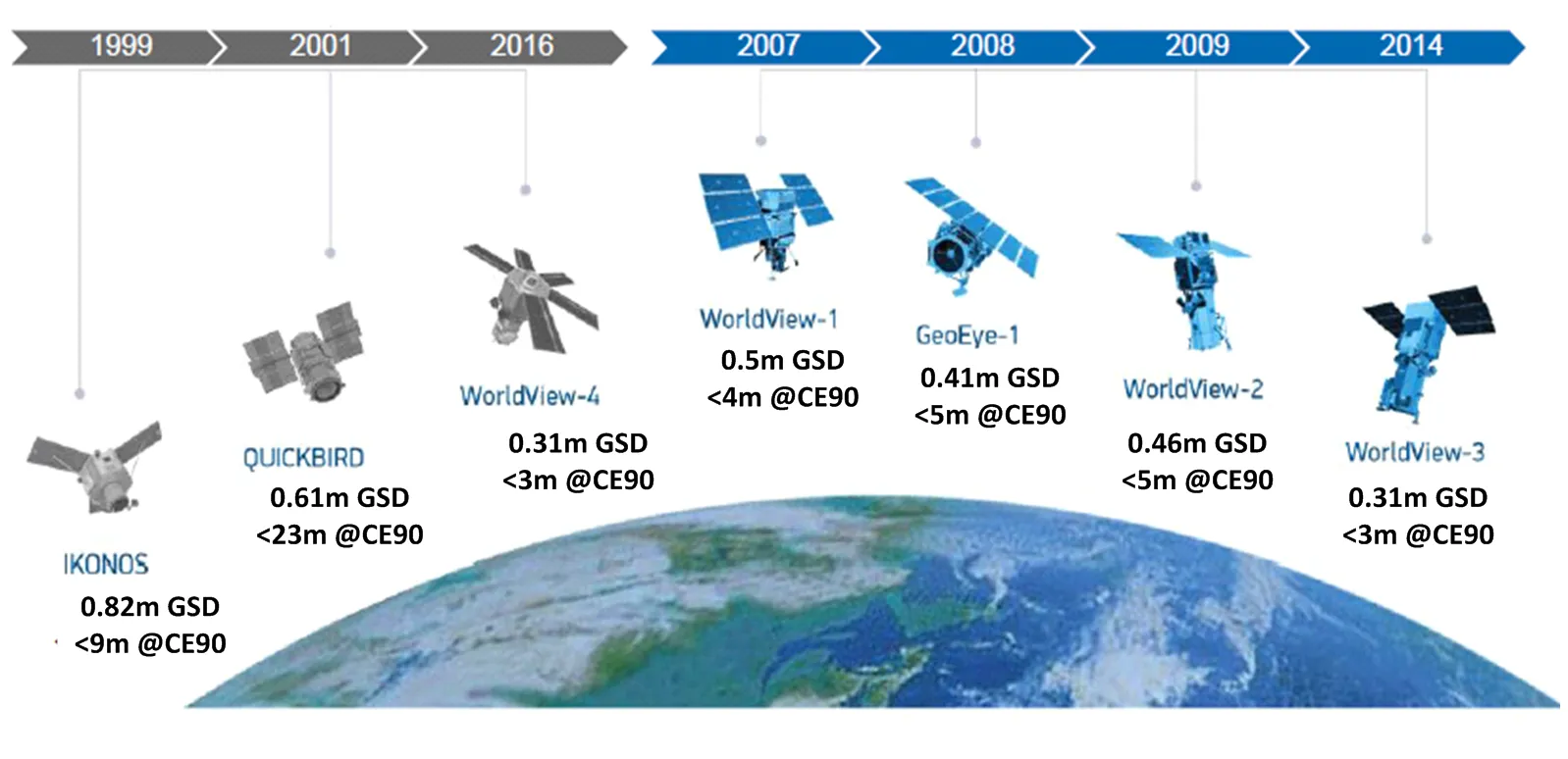
图1 美国高分商业光学遥感卫星的分辨率和平面定位精度示意

1 物理几何模型分析

高分辨率光学遥感卫星平面定位精度的物理几何模型通常都基于共线方程，重点考虑卫星自身要素的影响，使用光学遥感器内方位元素和卫星平台姿轨外方位元素共同建立物理几何模型，来实现遥感图像的精确几何定位[6-8]。光学遥感器的内方位元素包括：光学参数（如主点和主距等）、镜头光学畸变、CCD探测器像素尺寸、CCD线阵扭曲等。一幅图像的外方位元素包括6个参数，其中3个是直线元素，用于描述摄影中心的空间坐标值；另外3个是角元素，用于描述像片的空间姿态。内外方位元素的确定精度主要决定着遥感图像的平面几何定位精度。另外，对于米级定位精度而言，光程差、大气折射和地球曲率与地形等外部环境因素的影响也不能忽略，存在较大的偏置，需要通过建模予以消除。

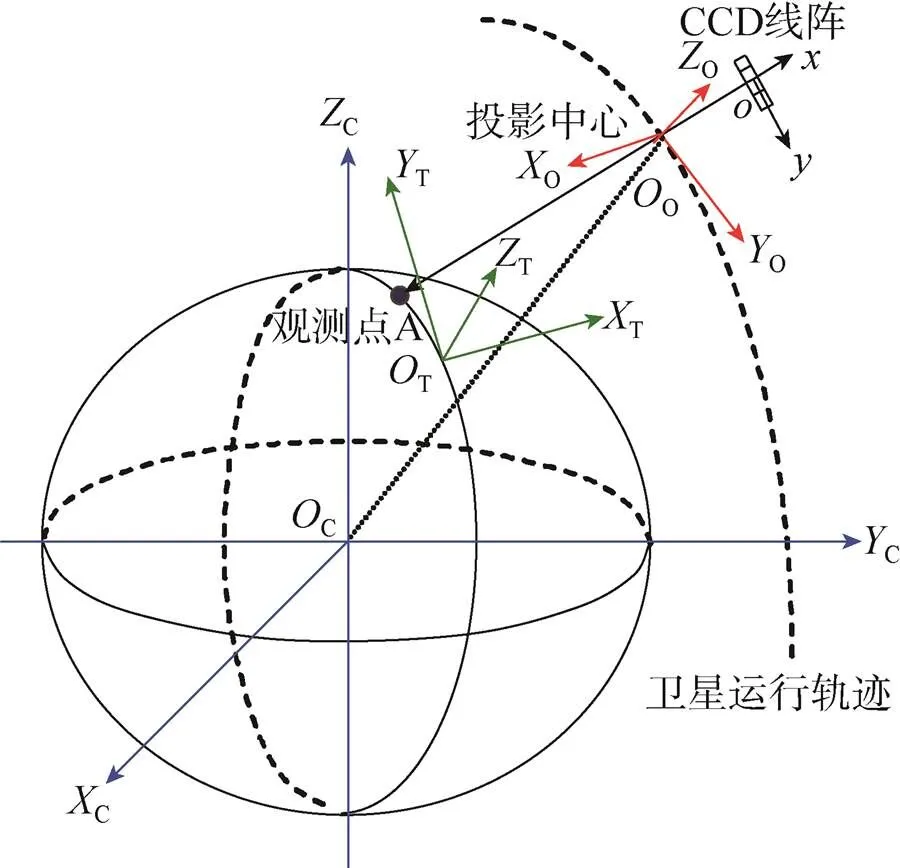
图2 光学遥感卫星几何定位的坐标关系示意

卫星物理几何模型建立过程中，物方空间坐标一般表示在地心直角坐标系C-CCC中，如图2所示，卫星几何定位就是要将某像点在线阵相机坐标系-中的坐标（,）变换为地心直角坐标系C-CCC中的坐标（A,A,A）。由于地心直角坐标数值很大，通常采用局部切平面直角坐标系T-TTT作为物空间坐标系的过渡坐标系，先确定了物点在T-TTT中的坐标之后，再将其变换到C-CCC坐标系中。对于线阵推扫式成像而言，在线阵坐标系中，设第0行第列上某个像素点的坐标为（0,y），对应的地面点物方空间坐标为（A,A,A），从相机坐标到物空间坐标需要经过一系列的正交变换，可归结为

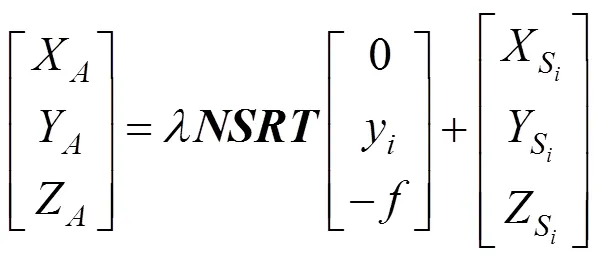
式中为尺度因子；为相机主距；为地心直角坐标系C-CCC与局部切平面坐标系T-TTT间的变换矩阵；为卫星轨道坐标系O-OOO到地心直角坐标系C-CCC的变换矩阵，由卫星平台的空间位置及速度矢量决定；为卫星本体坐标系B-BBB与轨道坐标系O-OOO间的变换矩阵，由成像姿态的俯仰、滚动和偏航角确定；为成像光束从相机坐标系-到卫星本体坐标系B-BBB的变换矩阵；（X，Y，Z）为第扫描行投影中心的物方空间坐标。

由式（1）并基于共线方程，可建立相机传感器坐标与物方空间坐标之间的关系如下

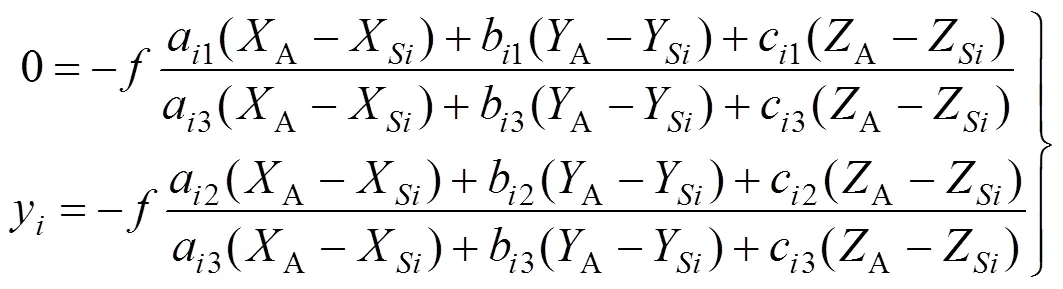
式中a，b，c（=1, 2, 3）为正交变换矩阵=的方向余弦值，具体形式为

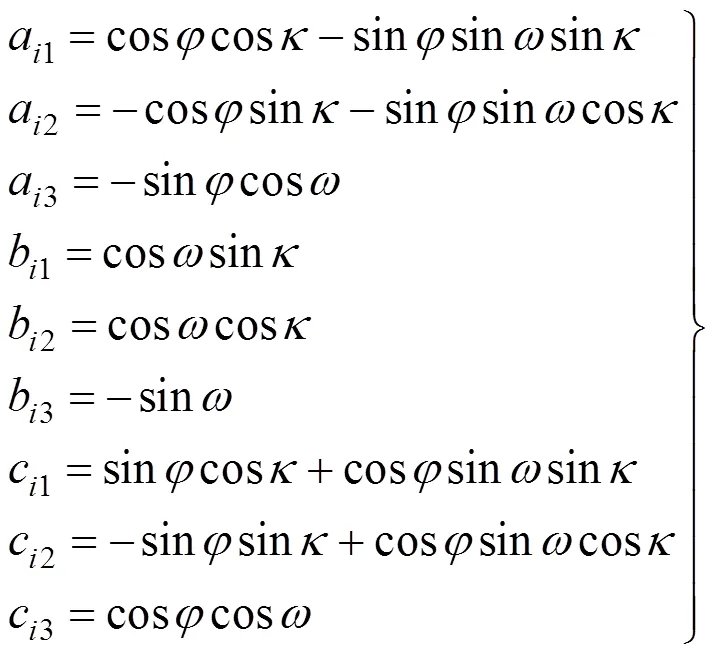
式中，，分别为卫星的俯仰角、滚动角和偏航角。

目前，高分辨率光学遥感卫星一般都安装高性能的定轨测姿系统如GPS、DORIS等，可以按照一定频率获取图像外方位位置元素，定轨系统测定的位置可达到厘米级精度；星敏感器、激光陀螺等可以按照一定频率获取图像外方位角度元素，星敏感器测定的姿态角可以达到角秒级精度。利用定轨测姿系统提供的离散外方位元素观测值，采用适当的滤波和内插算法可以获得每一扫描行图像的外方位元素，从而得到变换矩阵中的位置元素和变换矩阵中的角度元素。一般通过实验室精密的内方位标定测试得到变换矩阵中的位置元素和角元素的初始值，然后在卫星入轨之后再定期进行精确的在轨标定[9-10]。

对于平面定位精度而言，当不考虑模型误差及其他复杂畸变因素时，对地目标绝对定位精度主要取决于NSRT变换中角元素的精度，即变换中卫星的姿态角确定精度和变换中安装角度确定精度。卫星运行轨道越高影响越大，是对地目标定位的主要误差源[11-12]。综合起来的角元素主要由光轴指向角度确定精度所表征，其中沿俯仰和滚动方向的光轴指向角度对定位精度的影响较大，而偏航方向的光轴指向角度影响相对较小[13]（影响示意见图3）。以=500km轨道高度为例，对应于滚动和俯仰方向=2.0″的光轴指向确定误差，在星下点的平面定位误差估计将达到5m左右；对于幅宽=20km，偏航方向=2.0″的光轴指向确定误差，在星下点的平面定位误差估计仅为0.1m。

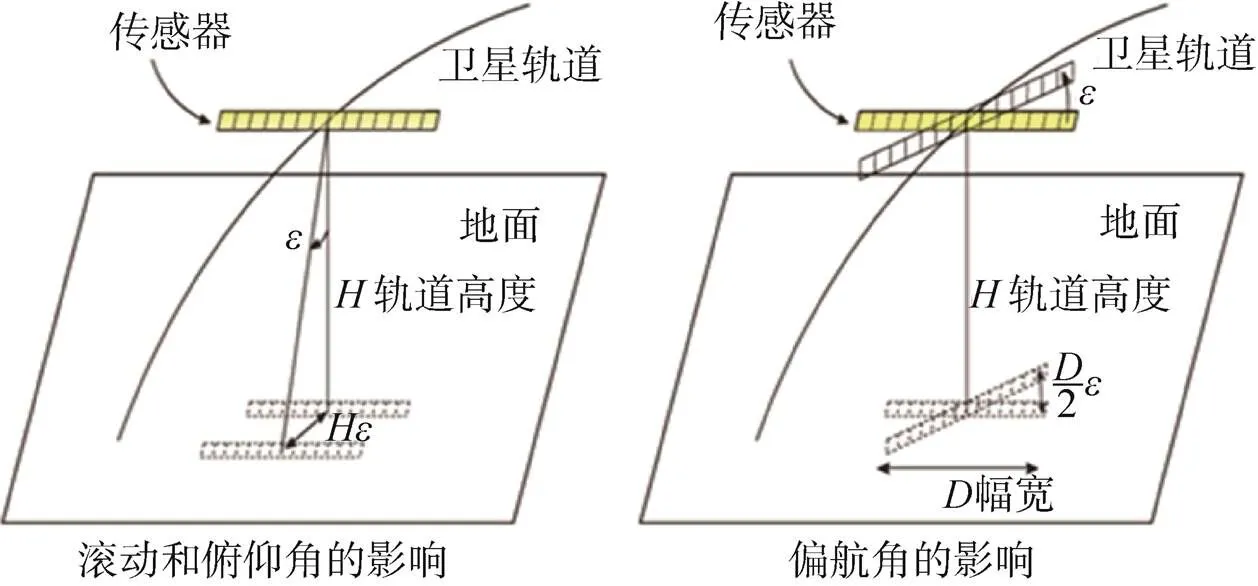
图3 光轴指向确定误差对定位精度的影响示意

另外，光程差和大气折射等要素造成物理几何定位模型的非严密，使得基于共线方程的物理几何定位存在一定的误差。尤其是高分辨率的敏捷成像卫星，有必要针对卫星非星下点对地不同角度成像的特点，进一步提升卫星成像物理几何模型的精度。卫星在轨飞行成像过程中约7.4km/s的飞行速度，相对于光速而言存在一定的相对运动，使得真实光轴和视轴之间存在大约25μrad的角度偏差（如图4所示）。光程差对于目标的平面几何定位精度有较大的影响，但通常未引起足够的重视，需要通过式（4）所示的数学模型进行分析和校正[14-16]。对于500km轨道高度星下点成像而言，在飞行方向大约会偏离25μrad×500km≈13m。

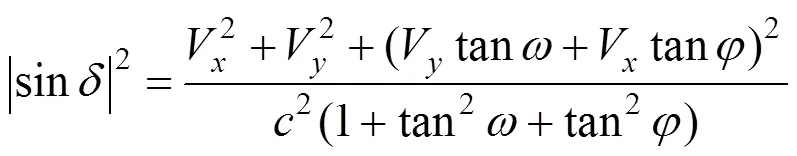
式中为角度偏差；V为方向的飞行速度；V为方向的飞行速度；为光速。

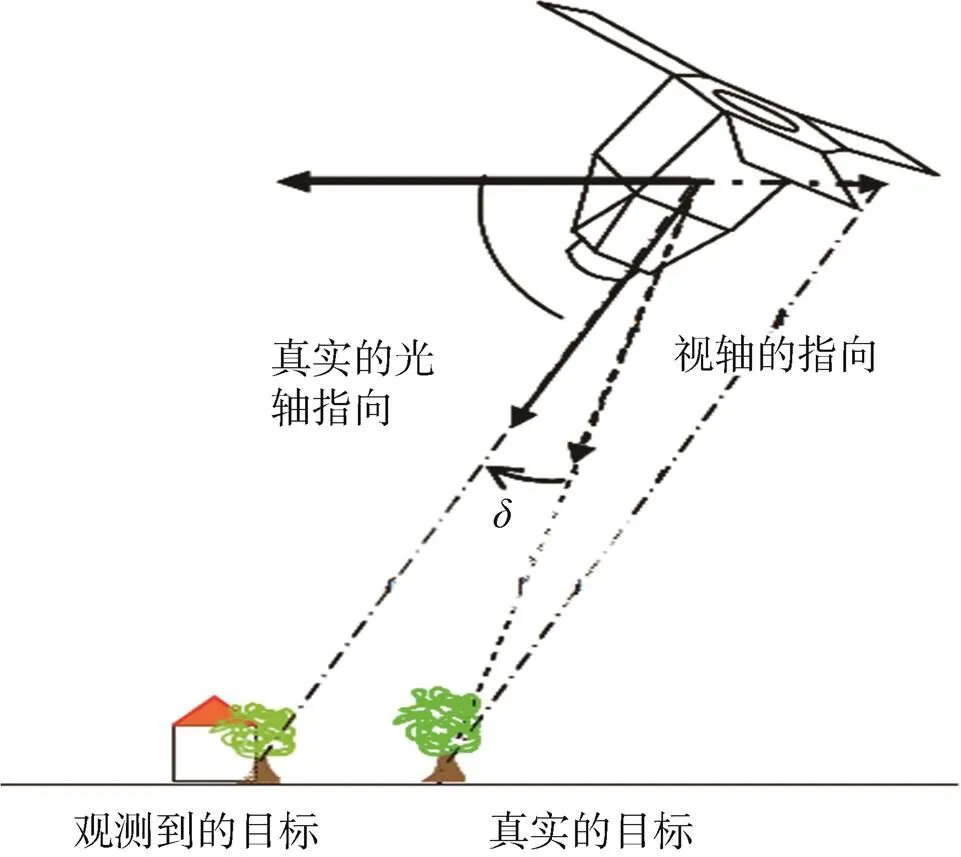
图4 光程差对定位精度的影响示意

同时，受到光轴传播路径大气折射的影响，大气折射会改变地物反射太阳光在星地间的直线传播方向（如图5所示），对于星下点成像大气折射的影响可以忽略，但对于非星下点尤其是较大角度成像而言，存在一定的大气折射误差[16-17]。

大气折射效应可以表示为

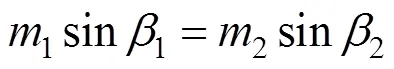
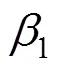
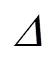
2 通用定位模型分析

物理几何模型需要精确的内外方位元素，使用起来相对比较复杂。自从1999年IKONOS-2卫星商业运营后，通用几何模型因其简便的优势得到了广泛应用。该模型可以由物理几何模型拟合求解得到，两者近似等效。但通用几何模型具有不依赖于具体的遥感器类型、拟合精度高、内插性能好的特点，表现形式简单直观，便于计算和使用[19-20]。最为常用的通用几何模型为RPC模型，图像产品一般都会自带一组与之对应的RPC参数（包括5个偏移系数，5个比例系数，4×20个多项式系数），利用有理多项式函数直接描述图像坐标（行列坐标）与地面坐标（经纬度和高程坐标）的几何关系。图像自带的PRC参数一般通过图像的内外方位元素，利用控制点对通用模型进行平差得到，由于消除了系统误差，因而具有更高的精度。有的卫星图像另外给出RPC–1函数的80个多项式系数，也可以通过RPC参数求拟得到RPC–1函数，从而描述地面坐标（，，）与图像坐标（，）的几何关系（如图6所示）。

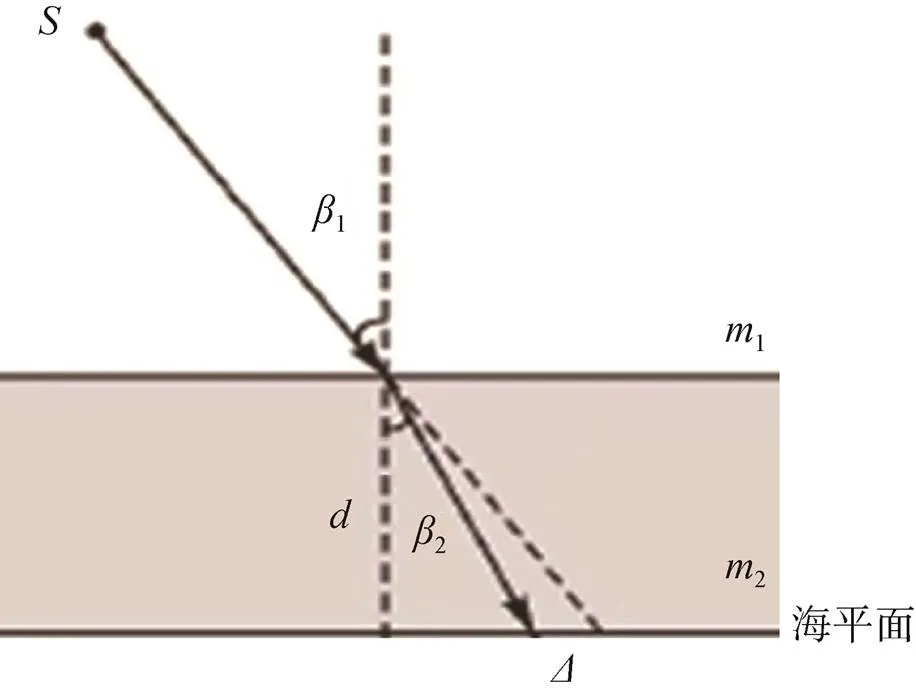
图5 大气折射对定位精度的影响示意

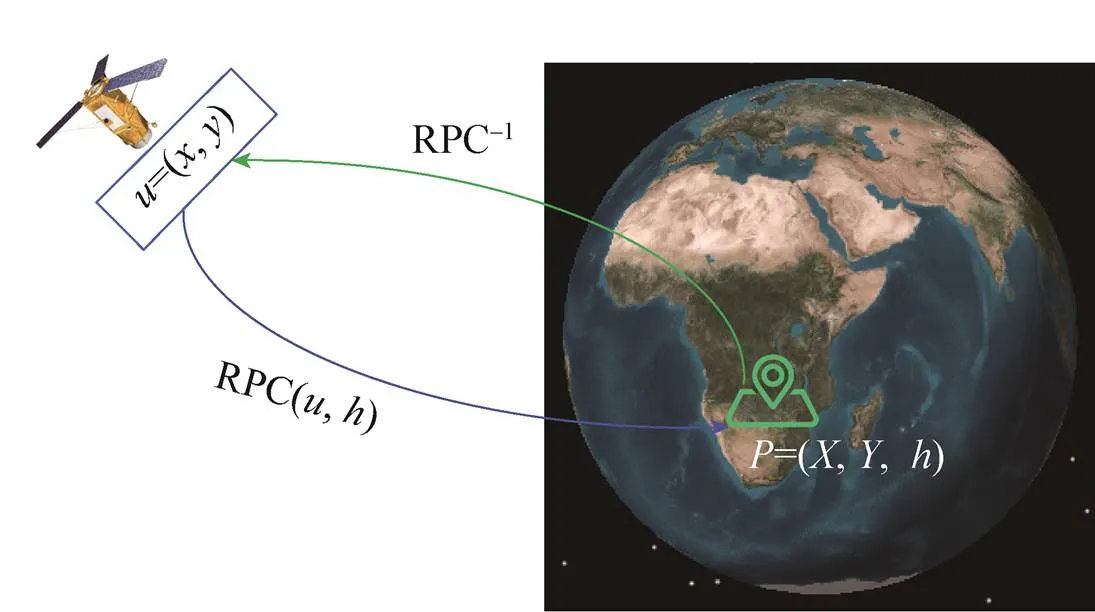
图6 通用几何定位RPC模型示意

RPC模型的一般表达形式为

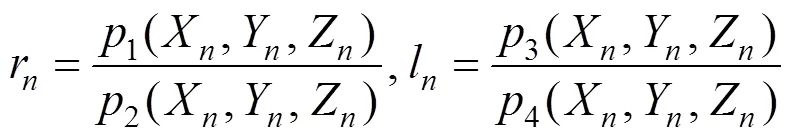
式中 （r，l）为图像上某像点的归一化行列坐标；（X，Y，Z）为该点对应的地面点的归一化位置坐标。有理多项式函数一般不高于3次，多项式的一次项的比值用来描述投影误差，二次项的比值用来描述地球曲率误差、大气折光差、镜头畸变差等；更高次项的比值用来描述其他一些未知的具有高阶分量的误差，如卫星平台的震动等。式（7）中RPC模型的1~4对应的三阶多项式展开形式为：

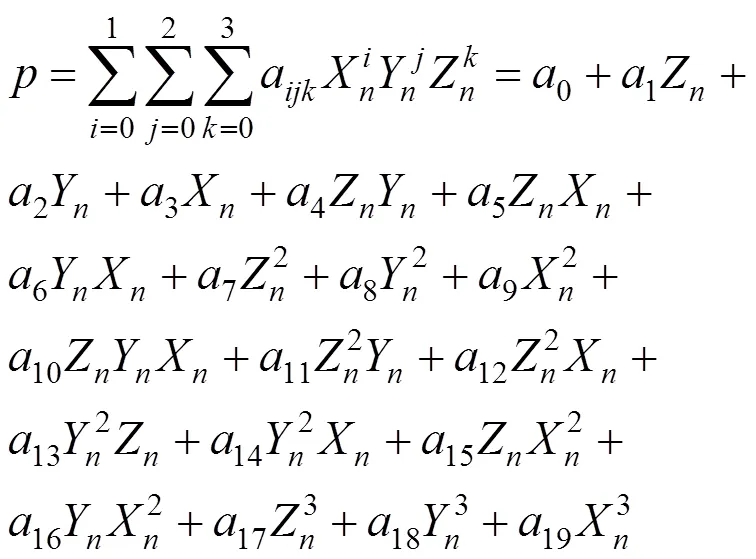
式中X，Y，Z为归一化的位置坐标；a为多项式展开通项式中的系数，其中0~19分别为具体展开后多项式各项的系数。

在无地面控制点条件下，利用“不依赖地形”方法，基于已知的物理几何模型生成虚拟控制点，通过虚拟控制点拟合求解得到RPC模型系数，求解流程如图7所示。

3 定位精度验证分析

利用美国Digital Global公司的WorldView-2卫星L1B图像产品数据，通过相应的物理几何模型生成虚拟控制点，并基于虚拟控制点求解相应的RPC参数。在没有地面控制点的情况下，以图像产品自带的RPC参数为参考基准，进行定位精度比较和验证分析，流程如图8所示。

图8 无控制点几何定位精度验证分析流程示意

测试数据如表1所示，其中D1类主要包括美国Digital Globe公司的WorldView-2卫星全色图像及辅助数据。图像分辨率为0.5m（重采样后），数据级别为L1B级（Basic），该级别数据已完成辐射校正（L1A）、传感器校正（L1B），没有进行几何纠正和正射纠正。对于Basic级图像产品，主要的图像支持数据文件包括：星历数据文件（.EPH），姿态数据文件（.ATT），几何校准文件（.GEO），图像元数据文件（.IMD）等。D2类主要为全球DEM数据（SRTM-GL1），DEM网格间距30m，公布的绝对高程精度为16m（标称精度），SRTM-GL1数据集的每个文件记录了3601×3601个采样点的高程数据。D3类数据主要是WorldView-2卫星L1B级别数据自带的RPC参数，为RPC00B文件（.RPB）和XML文件。最后，利用以上数据生成检查点格网（D4），在图像宽、图像高两个方向的格网密度均为虚拟控制点格网密度的2倍。

本文首先利用卫星的星历数据文件和姿态数据文件，通过物理几何模型建立像素坐标与地面定位坐标的单点定位转换关系，生成多个虚拟控制点网格，采用“不依赖地形”方法对RPC模型参数求解。再利用图像自带的RPC模型参数，进行几何定位精度的比较验证分析。

表1 测试数据文件

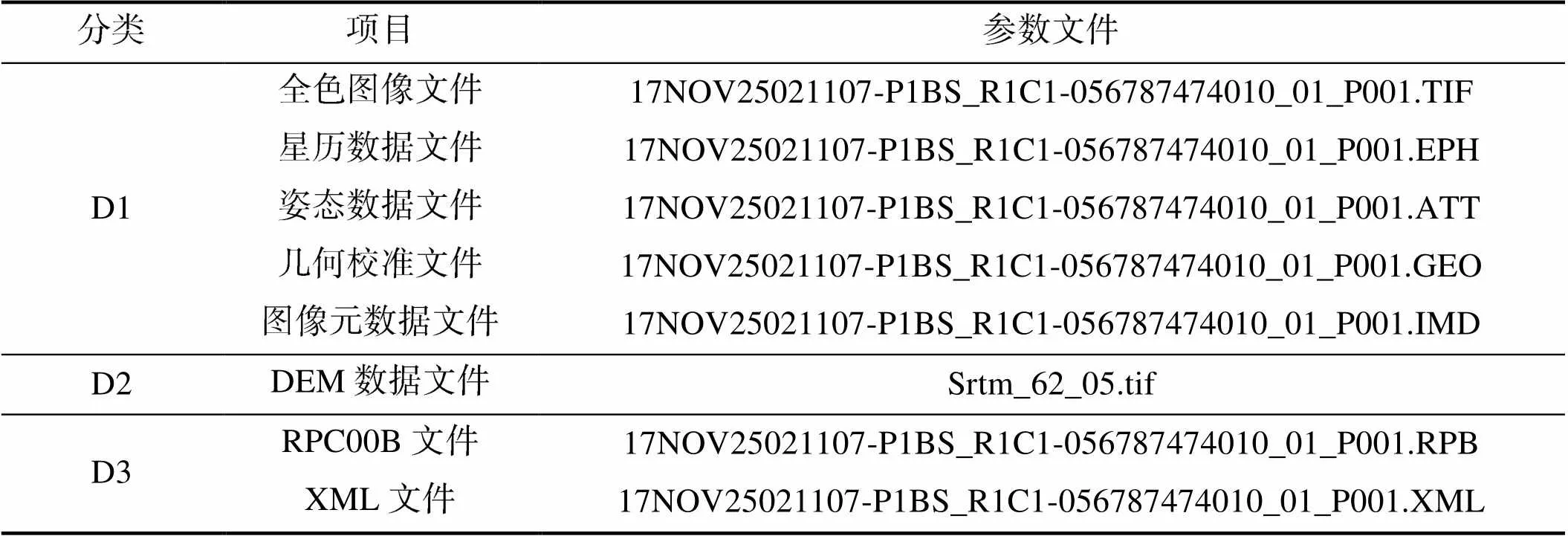
Tab.1 The data files of test

3.1 物理几何模型建立

通过以下多次坐标变换，建立物理几何定位模型，实现像素坐标到地面定位坐标的求解转换。

（1）地面坐标到飞行器坐标的转换

由.ATT和.EPH文件可以得到7个参数：S，S，S，1，2，3，4。将ATT文件中的四元数（1,2,3,4）转换为如式（9）所示的旋转矩阵1，实现从地心旋转坐标系下地面坐标（E,E,E）到飞行器坐标（S,S,S）的转换，即

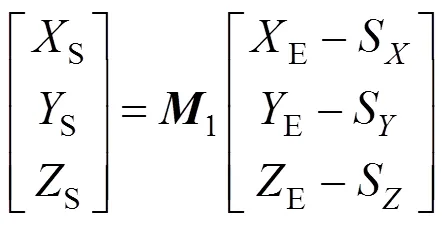
（2）飞行器坐标到相机坐标的转换

由.GEO文件可以得到7个参数，包括投影中心参数C,C,C，相机安装参数qcs1, qcs2, qcs3, qcs4。同式（9）的方式类似，分别对应到1，2，3，4，将GEO文件中的四元数（qcs1, qcs2, qcs3, qcs4）转换为旋转矩阵2，实现飞行器坐标（S,S,S）到相机坐标（C,C,C）的转换，即

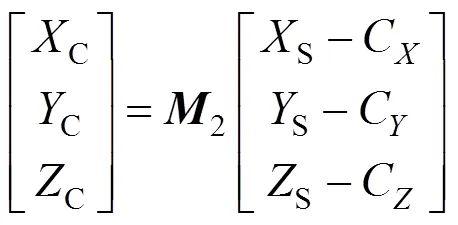
（3）相机坐标到像点坐标（，）的转换

在.GEO文件中，读取主点坐标（detOriginX，detOriginY），像元大小detPitch，主距ƒ和安装角度=detRotAngle等参数。通过坐标平移、角度旋转矩阵3（式（12））和尺度缩放变换，实现相机坐标（C,C,C）到像点坐标（,）的转换，转换公式为

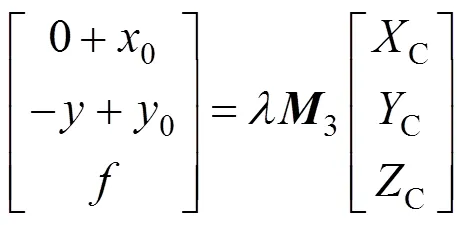
式中0=detOriginX/detPitch，0=detOriginY/detPitch；为缩放比例因子。

综合以上，得到物理几何定位方程为

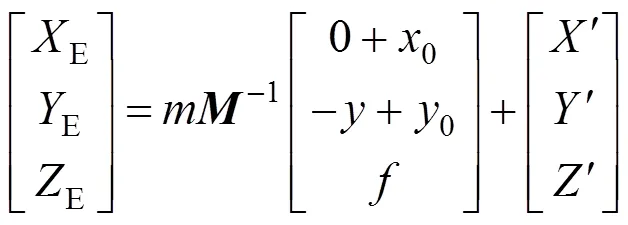
式（14）可以简化为

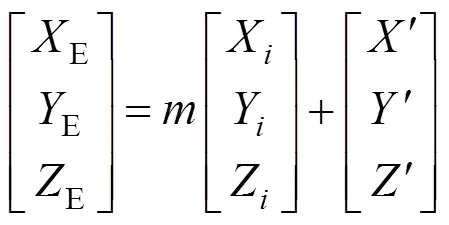
（4）物理几何模型定位方程解算

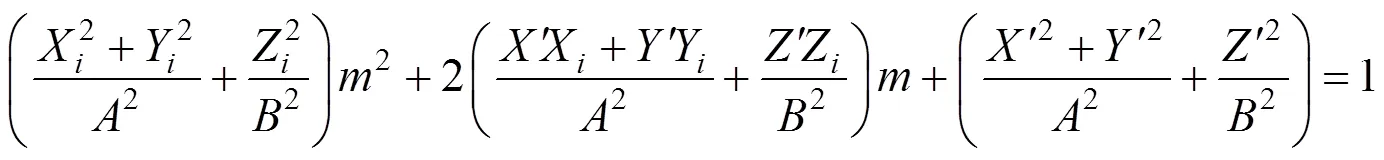
式中=+，=+，其中=6378137.0m，=6356752.3m分别为WGS84坐标系地球椭球的长半轴和短半轴；为地面点的椭球高，在SRTM数据的支持下，可通过地面坐标内插得到。

求解式（16）关于的二次方程得到两个不同的解，取较小一个作为正解；然后计算得到该点在WGS84坐标系下的三维直角坐标（X，Y，Z），进而可以转换得到经度、纬度和高程的数据（X，Y，h），完成从图像坐标（,）到地面坐标（E,E,E）的单点定位解算。

3.2 不依赖地形的RPC参数生成

基于图像当中的多个单点定位，通过虚拟控制点网格，采用“不依赖地形”方法，实现RPC参数的拟合求解。

（1）虚拟控制点网格生成

将图像划分为20×20个格网，则产生21×21个格网点。在SRTM数据的支持下，将在图像范围内获得的高程范围[36,1207]m划分为5个等距高程面。根据严密模型几何定位方程，对于每一高程面上的格网点（x，y，h），解算其对应的空间三维坐标并转化为经纬度的形式（X，Y，h），整体输出为（x，y，X，Y，h）的形式。同理，将图像划分为40×40个格网，输出这种2倍密度的虚拟控制点网格作为RPC参数精度的检查点。

（2）不依赖地形的RPC参数解算

基于虚拟控制点，采用“不依赖地形”方法对RPC模型求解。由于图像坐标和地面坐标尺度差异，容易引起数值解的不稳定性，先将像点图像坐标（x，y）、经纬度和高程坐标（X，Y，h）进行如式（17）所示的正则化处理，使坐标范围在[–1, 1]之间。

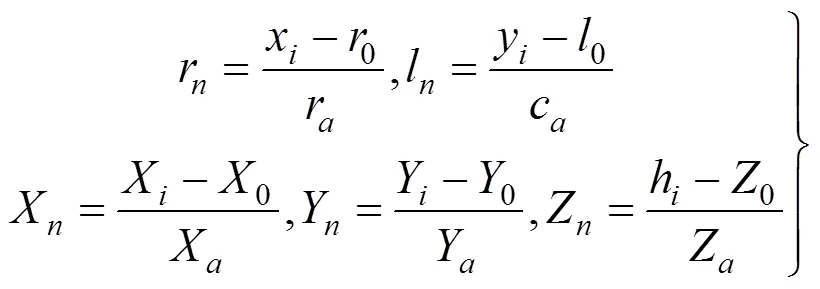
式中0，0，0，0，0是5个偏移系数；r，l，X，Y，Z是5个比例系数，通过对虚拟控制点统计计算求得。根据最小二乘法原理，构建观测误差方程与法方程，基于直接解方法获得初值，同时与上一次计算得到的残差差值进行比较，直到小于某一门限值，从而获得更加严密和精确的RPC参数值（总共90个参数）。

3.3 几何定位精度比较验证分析

利用以上物理几何模型参数求解拟合生成的RPC参数，与Digital Globe公司图像产品自带的RPC参数对比（考虑到自带RPC参数已经进行了全链路的误差标定和处理，精度较高，可以作为参考基准数据）。分别基于图像角点法、检查点法和交叉验证法，进行几何定位精度的比较验证分析。

1）基于图像角点法，验证图像数据产品自带RPC参数的绝对几何定位精度。从图像产品XML辅助文件中读取图像4角点坐标参数与RPC参数，反解4个角点的图像坐标，验证图像数据产品自带RPC参数的绝对几何定位精度（如表2所示）。结果表明，该图像产品自带的RPC参数具有较高的绝对几何定位精度，行和列两个方向的几何定位误差均不超过0.2像素，能够作为几何精度分析检验的基准数据。

2）基于检查点方法，分析验证“不依赖地形”方法生成的RPC参数的内符合精度（相对精度）。将2倍密度的虚拟控制点网格作为RPC参数精度的检查点，利用（x，y，X，Y，h）中的物方坐标，反解各检查点（共计41×41×5=8405个点）的图像坐标（xʹ，yʹ），统计“不依赖地形”方法生成的RPC参数的内符合精度（如表3所示）。结果表明，基于“不依赖地形”方法生成的RPC参数具有较高的内符合精度，行和列两个方向的中误差均不超过0.15像素，能够排除因RPC参数解算可能引入的误差。

表2 图像产品自带RPC参数精度验证结果

Tab.2 The accuracy validation result of imagery product with RPC

表3 “不依赖地形”方法生成的RPC参数精度验证结果

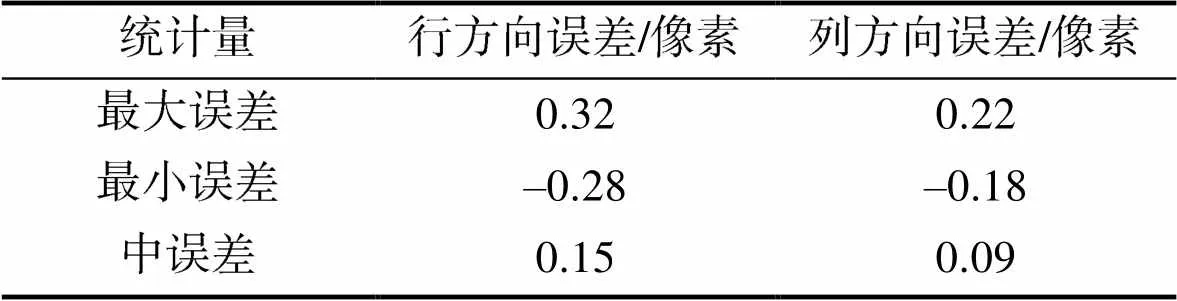
Tab.3 The accuracy validation result of produced RPC using independent of terrain

3）基于交叉验证法，分析验证两种来源RPC参数的交叉验证精度。基于2倍密度的虚拟控制点网格作为两种来源RPC参数精度的检查点，根据（x，y，X，Y，h）中的物方坐标，反解各检查点（共计41×41×5=8405个点）的图像坐标（1iʹ，1iʹ）、（2iʹ，2iʹ），统计“不依赖地形”方法生成的RPC参数、图像产品自带的RPC参数的相对精度（如表4所示）。结果表明，在仅仅考虑卫星内外方位元素的前提下，基于“不依赖地形”方法生成的RPC参数相对于图像产品自带RPC参数存在明显的系统性平移误差，行方向的中误差约39.90个像素（相当于19.95m），列方向的中误差约10.62像素（相当于5.31m）。这与美国Digital Globe公司对外公布的WorldView-2卫星无控制点定位精度优于5m（90%概率圆误差）的结果存在较大的偏差。

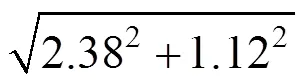
表4 两种来源RPC参数精度交叉验证结果

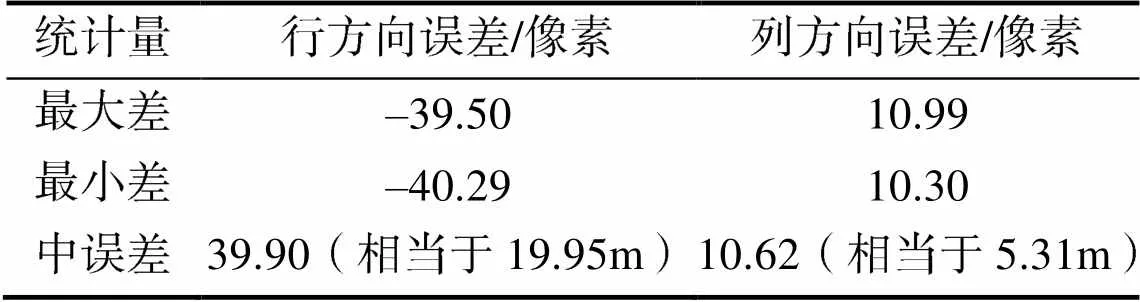
Tab.4 The accuracy cross-validation result of two RPC

表5 光程差和大气折射的定位偏移

Tab.5 the geolocation bias of light aberration and atmosphere refraction

4 结束语

本文对高分辨率敏捷卫星平面定位精度模型进行了全面的分析，通过对物理几何模型的分析，梳理出光轴指向确定精度是影响平面定位的核心要素，同时对于米级定位精度而言，在飞行方向的光程差也值得重点关注。通过卫星内外方位元素和RPC参数的拟合解算和转换，利用WorldView-2卫星数据进行了精度交叉验证，结果表明经过光程差和大气折射偏移之后，平面定位精度约为4.34m（90%概率圆误差），与公布的无控制点定位精度优于5m（90%概率圆误差）基本一致，说明了光程差和大气折射等偏差校正对米级定位误差的必要性。

[1] 王任享, 王建荣, 胡莘. 光学卫星摄影无控定位精度分析[J]. 测绘学报, 2017, 46(3): 332-337. WANG Renxiang, WANG Jianrong, HU Xin. Analysis of Location Accuracy without Ground Control Points of Optical Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 332-337. (in Chinese)

[2] 王建荣, 王任享, 胡莘. 光学摄影测量卫星发展[J]. 航天返回与遥感, 2020, 41(2): 12-16. WANG Jianrong, WANG Renxiang, HU Xin. Development of Optical Satellite Photogrammetry[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(2): 12-16. (in Chinese)

[3] 李德仁, 王密. 高分辨率光学卫星测绘技术综述[J]. 航天返回与遥感, 2020, 41(2): 1-11. LI Deren, WANG Mi. A Review of High Resolution Optical Satellite Surveying and Mapping Technology[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(2): 1-11. (in Chinese)

[4] 陈世平, 对地观测卫星遥感系统顶层设计的若干思考[J]. 航天器工程, 2013, 22(3): 1-7. CHEN Shiping. Some Considerations about Top-level Design of Satellite Remote Sensing System for Earth Observations [J]. Spacecraft Engineering, 2013, 22(3): 1-7. (in Chinese)

[5] 陈世平. 关于航天遥感的若干问题[J]. 航天返回与遥感, 2011, 32(3): 1-8.CHEN Shiping. Some Issues about Space Remote Sensing[J]. Spacecraft Recovery & Remote Sensing, 2011, 32(3): 1-8. (in Chinese)

[6] 曹海翊, 戴君, 张新伟, 等. “高分七号”高精度光学立体测绘卫星实现途径研究[J]. 航天返回与遥感, 2020, 41(2): 17-28. CAO Haiyi, DAI Jun, ZHANG Xinwei, et al. Study on the Development Approach of GF-7 High Precision Optical Stereo Mapping Satellite[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(2): 17-28. (in Chinese)

[7] CAO Haiyi , GAO Weijun , ZHANG Xinwei, et al. Overview of ZY-3 Satellite Research and Application[C]// Proceedings of the 63rd IAC (International Astronautical Congress): IAC-12-B1.3.3, Naples, Italy, Oct. 1-5, 2012.

[8] 孙立, 王长杰, 朱永红, 等. “高分七号”卫星双线阵相机高稳定性设计与分析[J]. 航天返回与遥感, 2020, 41(2): 47-57. SUN Li, WANG Changjie, ZHU Yonghong, et al. High Stability Design and Analysis for the Dual Line Array Camera of GF-7 Satellite[J]. Spacecraft Recovery & Remote Sensing, 2020, 41(2): 47-57. (in Chinese)

[9] 袁修孝, 余俊鹏. 高分辨率卫星遥感图像的姿态角常差检校[J]. 测绘学报, 2008, 37(1): 36-41. YUAN Xiuxiao, YU Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery[J].Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 36-41. (in Chinese)

[10] 范大昭, 刘楚斌, 雷蓉, 等. 资源三号卫星全色图像的姿态角常差检测[J]. 地理信息世界, 2013(4): 37-40. FAN Dazhao, LIU Chubin, LEI Rong, et al.Detection of Constant Angular Error for ZY03 Panchromatic Imagery[J]. Geomatics World, 2013(4): 37-40. (in Chinese)

[11] SAUVAGE D, GAUDIN-DELRIEU C, TOURNIER T. Model of the Lines of Sight for an Off-axis Optical Instrument Pleiades[C]//Proceedings of the 6th International Conferences on Space Optics, ESTEC. Noovdwijk, the Netherlands: [s.n.], 2006.

[12] DE FRANCHIS C, MEINHARDT-LLOPIS E, MICHEL J, et al. On Stereo-Rectification of Pushbroom Images[C]// Proceedings of the 2014 IEEE International Conference on Image Processing. [S.l.]: IEEE, 2014.

[13] DE FRANCHIS C, MEINHARDT-LLOPIS E, MICHEL J, et al. Automatic Sensor Orientation Refinement of Pleiades Stereo[EB/OL].[2020-09-01].http://dx.doi.org/10.1109/IGARSS.2014.6946762.

[14] GRESLOU D, DE LUSSY F, MONTEL J. Light Aberration Effect in HR Geometric Model[C]//Proceedings of The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences,Volume XXXVII-B1. Beijing: [s.n.], 2008: 859-864.

[15] DE LUSSY F , GRESLOU D, DECHOZ C, et al. Pleiades HR in Flight Geometrical Calibration: Location and Mapping of the Focal Plane[C]//Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XXXIX-B1. Melbourne: [s.n.], 2012: 519-523.

[16] 严明, 王智勇, 汪承义, 等. 大气折射对光学卫星遥感图像几何定位的影响分析[J]. 测绘学报, 2015, 44(9): 995-1002. YAN Ming, WANG Zhiyong, WANG Chengyi, et al．Atmosphere Refraction Effects in Object Locating for Optical Satellite Remote Sensing Images[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 995-1002. (in Chinese)

[17] TAO V. HU Y. A Comprehensive Study on the Rational Function Model for Photogrammetric Processing[J]. Photogrammetric Engineering and Remote Sensing, 2001, 67(12): 1347-1357.

[18] ASTRIUM-GEO. Pleiades Imagery User Guide V2.0[DB/OL]. (2012-02-01)[2020-09-01]. http://www.geo-airbusds.com/en/ 4572-pleiades-technical-documents.

[19] 胡安文, 张祖勋. 对高分辨率遥感图像基于仿射变换的严密几何模型的讨论[J]. 武汉大学学报(信息科学版), 2006, 31(2): 104-107. HU Anwen, ZHANG Zuxun. Discussion on Strict Geometric Model Based on Affine Transformation for Remote Sensing Image with High Resolution[J]. Geomatics and Information Science of Wuhan University, 2006, 31(2): 104-107. (in Chinese)

[20] DI K, MA R, LI R. Rational Functions and Potential for Rigorous Sensor Model Recovery[J]. Photogrammetric Engineering and Remote Sensing, 2003, 69(1): 33-41.

Error Analysis for Planar Geolocation Accuracy of Optical Remote Sensing Satellites

MAN Yiyun JIANG Zhijun

(Qian Xuesen Laboratory of Space Technology, Beijing 100094, China)

For optical remote sensing satellites with high resolution and agile imaging, in order to realize meter-level planar geolocation accuracy without ground control points, the systematical error should be calibrated with high accuracy and the random error should be effectively suppressed on the basis of error analysis of whole chains. Two geometric models are usually adopted in geolocation of the optical remote sensing satellite. The physical geometric models are based on the collinearity equation, which can establish the precision geometric models only by the interior and exterior orientation elements together. The light aberration and atmosphere refraction effects cannot be neglected and the bias must be eliminated during modeling. By the transformation between the physical geometric models and the generic geometric models, and the cross validation using WorldView-2 satellite imagery products and metadata files, the results show that after offsetting the bias of light aberration and atmosphere refraction, the planar geolocation accuracy is within 5m@CE90(90 percent circle error), showing the validity of this error analysis method.

optical remote sensing satellite; error analysis; planar geolocation accuracy; agile imaging; without ground control points

P237

A

1009-8518(2021)01-0135-10

10.3969/j.issn.1009-8518.2021.01.016

满益云，男，1978年生，2012年博士毕业于中国空间技术研究院飞行器设计专业，研究员。主要从事于全链路系统仿真分析与优化设计、高分辨率敏捷卫星成像技术、高精度测绘卫星技术等方面的基础研究工作。E-mail：man_yy@163.com。

2020-10-28

国防基础科研项目（JCKY2017203C108）

满益云, 江志军. 光学遥感卫星平面定位精度误差分析[J]. 航天返回与遥感, 2021, 42(1): 135-144.

MAN Yiyun, JIANG Zhijun. Error Analysis for Planar Geolocation Accuracy of Optical Remote Sensing Satellites[J]. Spacecraft Recovery & Remote Sensing, 2021, 42(1): 135-144. (in Chinese)

（编辑：夏淑密）