基于PCA-GA-BP的民航风险评价体系和预测模型*

（南京航空航天大学民航学院 南京 211106）

1 引言

近两年，我国民航业面临着多年少有的严峻复杂的国内外形势，仍旧处于稳步发展的阶段。根据中国民用航空局的发展统计公报，我国民航业的运输航空百万小时重大事故率十年滚动值为0.013，远低于世界平均水平0.153，安全的运行水平为行业发展提供了坚实的保障。因此，如何保持、提高民航安全水平一直是民航发展的重要问题。而与造成严重后果的各种事故相比，民航运营中出现更多的是事故征候和不安全事件。事故征候的出现是事故发生的表征［1］，若不对其采取有效的纠正与控制措施，在一定的触发因素作用下，就有可能转化为实际的事故，对其进行分析预测有助于减少潜在风险，提高安全水平。

目前对事故症候率的预测国内外也有了很多研究，杜毅［2］运用灰色理论，解决了无法精确地建立数学模型对飞行事故率和飞行事故征候率的关系进行描述的问题；王永刚，吕学梅［3］用灰色模型进行了事故征候之间的关联度分析；王永刚，郑红运［4］构建了航空运输事故征候的最优变权组合预测模型；张粉婷［5］运用Bow-tie方法对通用航空运行不安全因素进行研究，建立通用航空安全管理体系框架；于思璇，王华伟［6］运用稀疏降噪自编码算法，较为精确地通过当月的事故征候预测出当月的事故征候万架次率；孙瑞山等［7］用改进的关联度分析确定了影响民航事故征候的关键因素，并使用三角模糊数从时间序列进行了预测；Fullwood［8］等运用线性回归方法，基于事故数据预测了航空安全趋势；Abdoulaye Diamoutene［9］利用广义帕累托分布来预测未来的运营中极端通航事故的死亡人数。但是，以上方式均需要大量数据，有些不必要的指标数据收集增大了调查难度以及模型的计算速度。

本文提出了一种主成分分析法、遗传算法和神经网络相结合的算法，基于不安全事件对事故征候率进行预测。主成分分析过程中的因子分析为风险评价体系的优化提供了依据，且可以对指标进行降维，提高后续预测模型的运行速度。遗传算法对神经网络的初始权重和阈值进行了优化，提高了预测结果的稳定性，改善了神经网络模型易陷入局部最优的问题。

2 基于主成分分析法的风险评价体系

1）本文采用中国民航不安全事件统计分析报告中的分类方式，以原因对不安全事件进行分类，构建出如图1所示的初始的风险评价体系。

图1 初始风险评价体系

2）对原始数据进行标准化处理。假设进行主成分分析的指标变量有m个，分别为1，2，…，n，共有n个评价对象，第i个评价对象的第j个指标的取值 为aij。通过j=1，2，…m将各指标值转换成标准化指标值。其中 ，j=1，2，…，m，即，uj和sj为第j个指标的样本平均值和样本标准差。

3）主成分分析法计算相关系数矩阵R及风险评价体系优化。

指标间的相关系数计算结果如表1所示，从表中的数据进行分析，同一二级指标下的三级指标之间相关性较高，如雷击这一指标，与外来物击中、空中颠簸之间的相关系数高达0.908、0.962，而与其他指标的相关系数都较低或为负相关。但观察危险接近这一指标，与同为机组原因引发的重着陆指标相关性为负，而与空管原因引发的跑道入侵事件相关系数高达0.974，因此，对评价体系作出优化，如图2所示。

图2 优化后的风险评价体系

4）相关矩阵特征值和累计贡献率计算分析。其中贡献率bj计算公式为

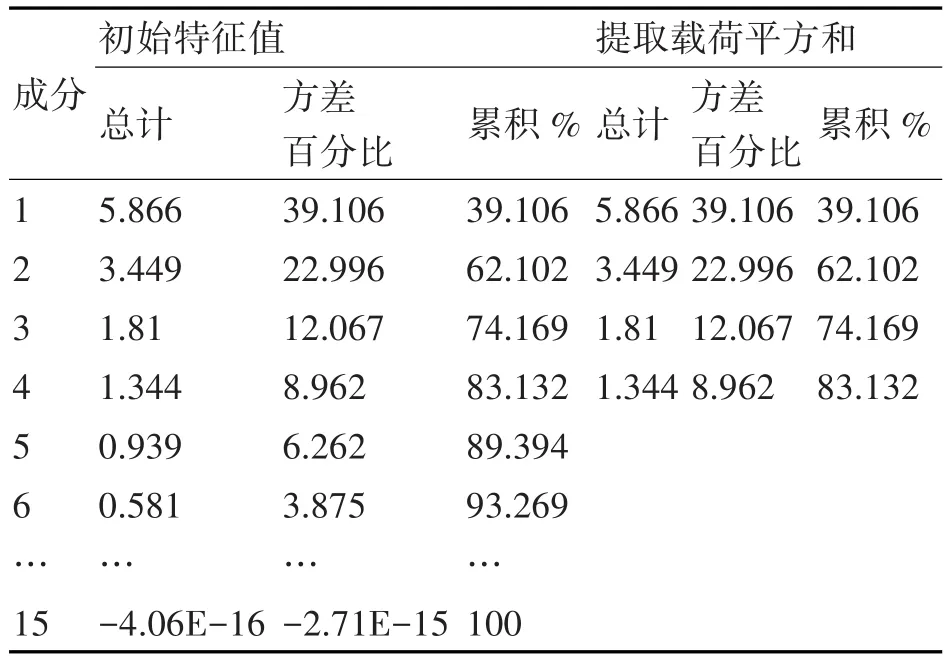
表2 主成分累计贡献率

选取初始特征值大于1的成分，从计算结果来看，这四个主成分累计贡献率达到了83.132%，已经包含了绝大部分的数据信息，因此，选取前四个成分作进一步分析。

表3 成分矩阵

根据成分矩阵和主成分贡献率结果，我们可以得出三级指标的贡献率排序：重着陆，外来物击中，机务维护、维修，空中颠簸，地面障碍物，雷击，空中失火、解体、冒烟，系统失效，燃油量低，客舱释压，通信中断，危险接近，跑道入侵，爆胎，迷航、偏航。其中，重着陆，外来物击中，机务维护、维修，跑道入侵，地面障碍物，雷击，空中失火、解体、冒烟，系统失效，燃油量低，客舱释压与主成分关联为正，因此选择这10个指标的数据进行风险预测。

3 GA-BP预测模型的构建与应用分析

3.1 BP模型

典型BP神经网络练过程分为前向传播和后向传播［10］，前向传播过程用于计算网络的输出，后向传播则是根据误差反馈调整网络权值和偏置，继续训练直到输出误差在允许范围内停止。

BP网络在初始化阶段，给每个网络权重和偏置一个很小的随机数，一般为（-1，1），祌经元的偏置可以看作是其自身的权重。记第p个样本在输出层第j个神经元节点的实际输出为ypj，期望输出为tpj，那么BP网络结构的误差指标函数为

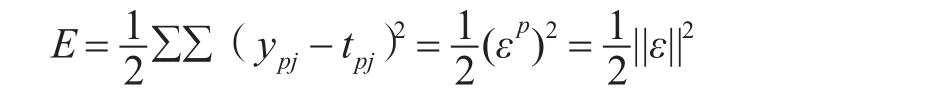
其中，ε是εp为元素的向量，其Jacabi矩阵记为J。BP网络各层神经元的连接权值用向量W表示，k表示迭代步数，则Wk表示第k次迭代的网络权值向量，下一步新的权值向量为Wk+1。已知移动量Wk+1-Wk很小，则ε的一阶泰勒级数及误差函数为

BP神经网络采用的是梯度最速下降法，沿负梯度方向迭代，使误差函数不断减小，直到取得最小误差后停止训练［11］。

梯度计算公式及梯度下降法的向量表达式，其中，参数μ的作用是控制迭代的步长［12］：

3.2 GA-BP模型

遗传算法是一种概率性的自适应迭代寻优过程，由于其适应度函数是不连续、无规则的，因此可以用来优化BP网络模型的初始权重和阈值，避免BP网络有时会陷入局部最优的问题，过程如图3所示。

图3 GA-BP算法流程图

3.3 GA-BP模型算例分析

3.3.1 GA-BP模型参数优化

1）迭代次数

将初始的迭代次数设置为50，对图4适应度曲线进行观察，可以看出在迭代次数接近10时，适应度已经趋于稳定，因此，设定模型的迭代次数为10。

图4 适应度曲线迭代次数图

2）神经网络隐含层节点数

图5 隐藏层节点数与准确率关系图

图6 预测结果图

3.3.2 模型性能对比分析

1）PCA-GA-BP与PCA-BP网络对比

如图7、图8对比图所示，PCA-GA-BP模型的10次运行准确率集中在91.5%～94.3%之间，平均准确率为93.444%，而PCA-BP模型的10次运行准确率集中在90.5%～94.1%之间，平均准确率为91.885%。两者进行对比，可以看出PCA-GA-BP模型的准确率更高，且运算准确率较为集中，模型的性能更加稳定。

图7 PCA-GA-BP与PCA-BP模型10次运行结果箱线图

图8 PCA-GA-BP与PCA-BP模型10次运行结果对比图

2）PCA-GA-BP与GA-BP网络对比

图9为PCA-GA-BP与GA-BP模型10次运行结果［13］，PCA-GA-BP 模型的平均准确率为93.444%，而GA-BP模型的平均准确率为93.445%。两个模型之间的预测准确率较为接近，证明主成分分析法筛选的指标较为完整地保留了特征信息。图10为PCA-GA-BP与GA-BP模型10次运行时间对比，可以看出相比于直接将数据输入GA-BP模型计算，PCA-GA-BP模型先对数据进行降维再进行运算，大大降低了运算时间。综合PCA-GA-BP与GA-BP模型的运算精度与运算时间结果，可以看出PCA-GA-BP模型在降低预测精确度的基础上大大提高了运行速度。

图9 PCA-GA-BP与GA-BP模型10次运行结果对比图

图10 PCA-GA-BP与GA-BP模型10次运行时间对比图

4 结语

本文构建PCA-GA-BP组合预报模型对民航事故征率进行预测，并通过主成分分析中的因子相关性分析结果得到了优化的民航风险评价体系。模型经过数次参数调试，选取了10作为迭代次数，13作为隐藏层节点数。研究结果表面，PCA-GABP模型的准确率达到93.444%，远高于BP模型91.885%的准确率，并与GA-BP模型93.445%的准确率相近，且运行速度仅为GA-BP模型的一半。PCA-GA-BP科学地对数据进行了降维，保留了记录主要特征信息的指标，提高了预测的精确度和速度，为民航事故征候率预测提供了更为科学的办法，有一定的推广价值。

本文对模型进行了多次重复实验来验证模型的稳定性。实验结果表明，PCA-GA-BP模型的10次运行准确率集中在91.5%～94.3%之间，而PCABP模型的10次运行准确率集中在90.5%～94.1%之间，PCA-GA-BP模型的预测结果更加稳定且更加精确，有效地避免了神经网络易陷入局部最优的问题。

所采集到的不安全事件数据比较有限，如果样本量增大，会进一步提高模型精度，未来可以采取数据迁移学习等方式来弥补样本量不足的问题，进一步提高模型的精度。