随机超曲面模型容积卡尔曼扩展目标跟踪算法*
(兰州理工大学电气工程与信息工程学院 兰州 730050)
1 引言
目标跟踪是指基于噪声传感器量测连续确定动态目标状态的过程。大多数目标跟踪算法是基于点目标模型的,即目标在每个采样周期内最多只生成一个量测值,这就导致对目标的状态识别较为单一,仅能依据单一量测信息对目标的运动状态进行识别。然而,随着高分辨率传感器在目标跟踪领域的广泛应用,每个目标在每个每个采样周期将对应多个传感器量测值,称这样的目标为扩展目标(Extended Target,ET)。近几年来,扩展目标跟踪(ET Tracking,ETT)[1~2]问题引起了学者们的极大关注。通过充分利用ET的多个量测信息可以对其进行更为深入的跟踪识别,即在实时跟踪目标运动状态信息的同时对目标的扩展状态信息也进行一定程度的识别。
众所周知,目标的形状(轮廓)信息是扩展目标最为典型也最为重要的特征之一。因此,实现对扩展目标形状的精确估计是提高扩展目标识别的关键所在。而完成扩展目标形状的准确建模是实现形状精确估计的前提。近些年来,对扩展目标形状估计的研究已经取得了一定的成果[3~5],提出了各种扩展目标跟踪算法。这些算法中绝大多数是基于扩展目标的形状参数化建模,而随机矩阵模型(Random Matrix Model,RMM)[6~8]是其最为典型的参数化建模方法之一。RMM在利用椭圆近似参数化表示扩展目标形状特征的基础上,利用高斯逆Wishart分布来描述目标的扩展状态密度。但是,仅仅利用椭圆近似描述扩展目标的形状较为粗略,这就导致不能准确估计出扩展目标的局部复杂轮廓特征。而Baum提出扩展目标量测源的近似非参数随机超曲面模型(Random Hypersurface Model,RHM)[9~12]较好地弥补了RMM的缺陷,RHM非参数模型的核心思想是利用星凸参数曲面估计扩展目标的形状。具体而言,RHM是在利用径向函数描述星凸形扩展目标形状的基础上,对径向函数进行有限阶的傅里叶级数展开,通过展开的系数完成扩展目标形状参数化建模,再结合尺度因子缩放扩展目标的轮廓完成对其表面量测源的建模。在这种方式建模下,选取的傅里叶级数的阶数越高也就意味着对扩展目标的形状估计越精确。但是,这种建模方式下扩展目标量测源的方程具有较强的非线性。因此,本文利用Arasaratnam提出的具有高滤波精度和数值稳定性的容积卡尔曼滤波(Cubature Kalman Filter,CKF)[13~14]算法对扩展目标 RHM 的非线性伪量测方程的高斯加权积分进行近似,进而完成对不规则形状扩展目标的跟踪估计。
本文针对不规则形状星凸形扩展目标的跟踪问题。首先利用RHM对星凸形扩展目标的形状进行建模。然后详细推导了基于RHM的CKF扩展目标跟踪算法。此外,文中分别利用均方根误差和拟Jaccard距离[15]对扩展目标的运动参数估计和形状估计进行评测。最后,通过构造多种具有不同形状的星凸形扩展目标的跟踪实验验证了本文跟踪算法的有效性。
2 随机超曲面模型星凸形扩展目标建模
本文研究的扩展目标类型为星凸形扩展目标,这种类型的目标轮廓可以完全通过径向函数描述。首先,星凸形可以定义为:如果一个形状参数向量为的扩展目标S(ek)中至少存在一个点,以至目标中其他点与连接的线段完全属于该目标,则称这样的扩展目标为星凸形扩展目标,其中目标参数向量为。
下面是利用RHM对扩展目标的形状建模过程:


3 RHM扩展目标容积卡尔曼滤波跟踪算法
RHM扩展目标容积卡尔曼滤波跟踪算法由预测步与量测更新步构成。首先,给出该算法的预测步,其预测步与传统的高斯滤波算法的预测步一样。
1)预测步


2)更新步
RHM扩展目标容积卡尔曼滤波跟踪算法量测更新步的核心是结合k时刻扩展目标的所有量测信息以及基于RHM建立的扩展目标的量测源模型完成对扩展目标运动状态和形状的估计。具体流程如下。
首先,计算基本容积点ξi以及相应的权值wi,即
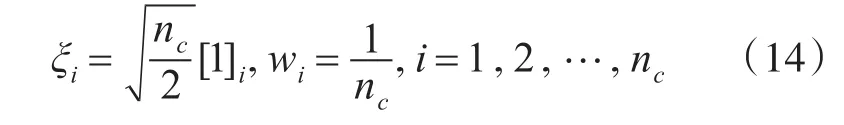
根据三阶容积规则可知容积点总数nc为扩展目标状态维数nx的2倍,即nc=2nx。完全对称点集[1]可通过对单位向量e=[1,0,…,0]T的元素进行全排列和改变元素符号的方式得到,其中单位向量e的维数与nx相等,[1]i表示完全对称点集[1]的第i个点。另外,由k时刻预测的扩展目标状态向量xk|k-1和协方差矩阵Pk|k-1根据下式计算容积点,即

最后,计算增益矩阵并结合伪量测0更新扩展目标的状态向量和协方差矩阵

4 扩展目标状态估计性能评价
不规则形状星凸形扩展目标的状态由运动状态与形状两部分构成。为了全面评估文中所提算法对扩展目标的跟踪性能。文中利用RMSE对目标质心位置估计进行评测,同时利用文献[15]提出的拟Jaccard距离对扩展目标的形状跟踪性能进行评价。
扩展目标质心位置评测指标RMSE的定义为:如果k时刻的扩展目标真实位置向量为mk,利用本文跟踪算法估计的位置为,那么RMSE的计算公式如下所示:

由拟Jaccard的计算公式可知,Jk的值越小,对扩展目标的形状估计越精确。
5 仿真实验
本文构造3种不同形状且做CV运动(匀速直线运动)的星凸形扩展目标进行跟踪仿真实验。仿真场景设定扩展目标的运动区域为[0 , 1000] m×[0 ,1000] m,扩展目标随时间的状态演化服从线性高斯模型。采样周期T=1s,采样50个时刻,扩展目标的形状参数的阶数nf=11。过程噪声标准差σw为0.03,量测噪声是协方差矩阵为R=diag(0.32,0.32)的高斯白噪声,尺度因子s~N( )2/3,1/18 。扩展目标在每个采样周期内产生的量测数服从均值λ=50的泊松分布。
场景1:设置目标的形状为十字架形,初始形状是半径为3的圆,初始状态服从均值和方差分别为

的高斯分布。在上述仿真场景下,利用RHM扩展目标容积卡尔曼滤波跟踪算法对扩展目标进行跟踪,跟踪结果如图1所示。

图1 十字架形扩展目标的跟踪效果图
由图1十字架形扩展目标的整体跟踪效果以及形状的局部放大图可知,文中所提的RHM扩展目标容积卡尔曼滤波跟踪算法能够同时实现对十字架形扩展目标质心和形状的精确估计。进一步,由图2给出的RMSE与评测形状估计效果的拟Jaccard距离的时间统计值看出,文中算法对十字架形扩展目标能够进行准确的定位,与此同时,随着量测信息的累积,对扩展目标的形状也能实现准确的估计。

图2 十字架形扩展目标RMSE与拟Jaccard距离
为了验证文中所提出的RHM扩展目标容积卡尔曼滤波跟踪算法的有效性和普适性,在上述仿真的基础上,进一步设定场景2与场景3进行仿真实验。
场景2:设定目标的真实形状为做CV运动的五角星,初始形状设置为半径为6的圆形,其他参数与场景1相同。仿真结果如下所示。
由图3和图4五角星形扩展目标的跟踪效果可得,当改变扩展目标的形状时,RHM扩展目标容积卡尔曼滤波跟踪算法也能够依据扩展目标的量测信息对扩展目标的位置和形状进行准确的估计。

图3 五角星形扩展目标的跟踪效果图

图4 五角星形扩展目标RMSE与拟Jaccard距离
场景3:设定扩展目标的真实形状为正方形,目标的初始形状为半径为4的圆形,同时改变目标的运动参数,即,其他参数与场景1和场景2相同。
由图5与图6正方形扩展目标的跟踪效果图可知,当改变扩展目标的运动速度和形状时,并不能影响文中提出的RHM扩展目标容积卡尔曼滤波跟踪算法的跟踪性能。

图5 正方形扩展目标的跟踪效果图

图6 正方形扩展目标RMSE与拟Jaccard距离
6 结语
本文针对不规则形状星凸形扩展目标的跟踪问题,首先利用RHM对扩展目标的量测源进行建模,其次利用径向函数对扩展目标的形状进行参数化表示。然后详细推导了基于RHM的容积卡尔曼扩展目标跟踪算法。最后,构造多种形状的星凸形扩展目标跟踪仿真,验证了本文所提算法的有效性。

