基于负熵最大化判据的ICA算法研究与应用*
(中国人民解放军92785部队 葫芦岛 125208)
1 引言
在传统的信号处理中,通常认为随机变量具有高斯分布特性。但在实际处理过程中,信号却具有非高斯分布特性,例如自然景物图像,声音,脑电信号等,满足高斯分布特性的信号少之又少,通过独立分量分析方法对信号进行处理不需要其满足高斯分布,是一种新的盲源分离(Blind Source Separation,BSS)技术[1~2],在一定条件下,其可以通过多通道信号观测有效分离出源信号,因此独立分量分析方法的研究具有广泛的应用前景。核心是以独立统计为依据,通过建立目标函数实现对信号源的分解、优化,进而实现对观测信号的分析。在独立分量分析过程中,一般建立不同的目标函数对信号的非高斯特征进行分析,为使其非高斯性达到最大,还需通过不同的优化算法对函数进行处理,最终达到ICA各分量尽可能相互统计独立的效果。本文简要介绍了独立分量分析问题的描述和预处理方法,分析了基于负熵最大化判据的FastICA算法,并将其应用于人脸特征提取,在人脸识别中得到了满意的结果。
2 基于负熵最大化判据的独立分量分析算法
2.1 ICA问题的描述和处理方法[3]
ICA问题可以描述为假设在m个通道中获取到m个信号xi=(i=1,2,…,m),则每个观测信号即是由n个独立源信号si=(i=1,2,…,n)的线性混合而成。即

其中,观测信号矢量矩阵为X=[x1,x2,…,xm]T,源信号矢量矩阵为S=[s1,s2,…,sn]T;A是尺寸为m×n的未知混合矩阵,也是ICA问题需要解决的方面。ICA解决的基本问题就是仅通过观测数据xi估计未知独立源si,或估计混合矩阵A。对于具有非高斯分布特证的信号而言,具体方法是寻找一个矩阵WI,使得

要求输出信号yi相互独立,则Y=[y1,y2,…,yn]T就是S的估计量。
首先对原始数据一般先进行预处理,可使ICA的工作量大大减少。在数据预处理中,数据的“白化”过程在其中起到至关重要的作用,实质上是利用线性变换得到各分量互不相关的新向量Z,并使Z的各个分量间互不相关,且必须满足E(ZZT)=I。利用奇异值分解(AVD)方法对X施加线性变换,假设一白化矩阵WP,可使Z=WPX。由矩阵分析理论知,Cx的协方差矩阵Cx=E(XXT)可分解为

其中WI=WWP,由E(YYT)=WE(zzT)WT=WWT=I可知,ICA的变换矩阵W是一个正交阵。由此可见,白化过程对ICA并不产生影响,且分离矩阵对原先估计矩阵而言,自由度大大减少,使得计算的复杂度有了显著降低。
2.2 基于负熵最大化判据的目标函数
熵往往用来衡量信息的不确定性。在所有等方差随机变量中,高斯分布的随机变量熵最大。基于这一特点需要引入负熵概念(Negentropy),区别非高特性的信号,建立函数实现对其度量。对任一随机变量x,其负熵[4~5]定义为

其中xG是具有和x相同方差的高斯变量,H(·)为随机变量的信息熵:

根据公式可知,当且仅当x满足高斯分布特征时,负熵值为零,当x服从其它非高斯分布特征时,由公式可知负熵的值始终大于零。当满足可逆的线性变换时,负熵的值保持不变因而,负熵可以用来对非高斯信号进行分析处理。但在负熵的计算中需估计随机变量的概率密度,计算量较大,为方便计算,对负熵进行合理有效近似,其中一种较好的负熵近似[6]:

其中,E(·)为均值计算,G(·)是一种非线性、非二次的函数,通常选择如下形式的G(·)函数:

由中心极限定理可得,随机信号在度量中可以通过非高斯性实现相互依赖,x的非高斯性越强,J(x)值越大,可以得知最大化负熵即为最大化非高斯特性。
2.3 基于负熵最大化判据的FastICA算法
FastICA算法分如下两步实现[7]:1)白化处理观测信号;2)提取独立分量。其中,步骤1)在上面已经分析过,下面着重分析独立分量的提取。白化过程解决了信号之间的相关性问题,将信号分解成为互相独立的信号,但并没有实现对图像的分离。需要寻找一个分离矩阵W实现对白化信号Z中的独立分量的提取。(注:此处提及的W是针对白化以后的信号Z而言的),分离矩阵W由迭代法不断逼近,假设变量n表示迭代步数,si为S中的某一分量,wi(n)为分离矩阵W(n)中,与si对应的某一行向量,即

利用定义目标函数度量si的非高斯性,每一次迭代过程对wi(n)进行优化,使其不断逼近分离矩阵。FastICA算法的调整公式为[8]

当相邻两次的wi(n)变化值较小或无变化时,可认为找到si,迭代完成。通过对时间平均获得式(12)中的均值。在迭代过程时要注意每次迭代后都要对wi(n)进行归一化处理(wi(n)=wi(n)/||wi(n)||)。对于多独立分量也可以采用此方法,需要注意的是需要在观测信号中减去提取出的独立分量,以此得到混合矩阵A和分离矩阵W。
3 FastICA算法在人脸特征提取中的应用
人脸特征提取及识别目前是国内外研究的一个重要方向,研究过程中发现,人脸的图像细节与高阶统计特征密切相关。ICA方法便是基于高阶统计特征,实现对多通道数据信息的处理分析,提取出图像内部的独立特征。
3.1 独立分量处理的人脸图像描述方法
本文对ICA标准人脸库进行分析,以此得到人脸识别统计的基本图像。如图1所示,源图像S经过线性混合后得到X,其中A为未知混合矩阵,满足X=AS。根据前文所述的方法,利用ICA方法估计分离矩阵WI,将原图像用分离矩阵从观测图像中分离,得到满足统计独立的输出矩阵Y。
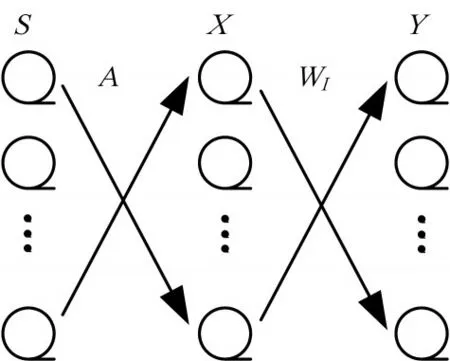
图1 基本ICA模型
输出矩阵Y=WIX的行向量是分离后的人脸基图像。
如图2所示,人脸图像是由独立基图像经过线性组合构成的,混合矩阵A由每张图人脸线性组合的系数构成,A同样可通过计算分离矩阵WI得到,。设xm为待识别人脸,在人脸空间中有

图2 ICA独立基图像描述

其中,(a1,a2,…,an)即为投影系数。
3.2 实验与分析
本实验采用CAS-PEAL标准人脸数据库[9]进行ICA识别测试。本文从该数据库中挑出400幅人脸图像,包括40个不同的测试者,每人10幅在不同姿态、表情、装饰和光照条件下的人脸图片。其中图片内容包括了不同时期、光照和表情变化,所有图像均为黑色背景。

图3 ORL人脸库中的部分人脸图像
首先将图像进行标准化处理,得到65×65像素的脸图,保证实验时人脸尺度的一致性;通过低通滤波手段,降低光照等对图片影响,将人脸特征突出。具体方法是,将每一幅65×65人脸按行展开为1×4225行向量,n幅人脸构成n×4225输入矩阵X。
按照3:2的要求组成训练集和测试集,其中训练集随机选择了70个测试者的照片。每人前6幅65×65图像构成,得到420×4225的原始矩阵X,后4幅图像构成测试集。将首先运用PCA方法[10~12]降低原始矩阵X维度。在该实验中,我们对数据进行降维50%,保留了96%的原始数据,将降维后的矩阵进行ICA处理,输出矩阵Y的每一行向量便是每份训练集人脸的基图像。由于每行向量之间互不相关,故其人脸图像的投影系数唯一代表着该图像,得到的系数构成混合矩阵A。此时,识别问题变成了系数的识别问题,可以利用分类器实现对人脸图像的识别。
4 结语
本文分析了基于负熵最大化判据的独立分量分析算法,并将其应用于人脸特征提取,在人脸识别中得到了满意的结果。由于ICA理论、算法仍不断在优化,后续许多问题的分析、处理方法都可以随之进行完善,包括对大量数据的人脸识别也成为后续该方法的研究重点。

