基于Copula函数的头道拐水沙关系频率分析研究

李弘瑞 李新杰 张红涛

摘 要：為了掌握黄河中游水沙关系的变化特点和变化趋势，基于黄河头道拐站1958—1990年33 a和1998—2017年20 a的水沙资料，通过P-Ⅲ型曲线分别建立年径流量与年输沙量的频率曲线，对年径流量和年输沙量进行丰平枯划分;基于Copula函数对水沙关系进行变异诊断，构建年径流量-年输沙量联合分布模型并通过拟合优度检验选取最合适的Copula函数，计算水沙丰平枯组合遭遇频率。结果表明：头道拐水文站在1958—1990年和1998—2017年的年径流量和年输沙量呈下降趋势，1990年水沙关系发生变异;1958—1990年水沙关系存在一个变异点（1965年），1998—2017年水沙关系不存在明显的变异点，整体水沙关系存在一定的平稳性;1966—1990年和1998—2017年两个时期的水沙丰平枯组合遭遇频率中丰枯同频高于丰枯异频，1966—1990年的年径流量和年输沙量在较大值处相关性较强，1998—2017年年径流量和年输沙量整体相关性较强，水量和沙量的丰平枯变化趋势基本一致。

关键词：水沙关系;联合分布;变异诊断;遭遇频率;头道拐水文站;黄河

Abstract： In order to grasp the characteristics and trends of the relationship between runoff and sediment at the upper and middle reaches of the Yellow River， based on the water and sediment volume data of the Yellow River Toudaoguai Station in the 33 years from 1958 to 1990 and the past 20 years from 1998 to 2017， the P-Ⅲ curve was adopted to establish the runoff and sediment discharge frequency and divide annual runoff and annual sediment transport into hight， medium and low flow. It carried out mutation diagnosis of runoff and sediment relationship， and joint distribution model of annual runoff and annual sediment transport was constructed based on copula function by the goodness of fit test. Finally， it calculated the encounter frequency of wet-normal-dry runoff and sediment combination. The results show that the annual runoff and sediment discharge of Toudaoguai Hydrological Station in 1958-1990 and 1998-2017 show a downward trend and the relationship between runoff and sediment is remarkable especially after 1990; There is a variation point （1965） in the relationship between water and sediment during 1958-1990. There is no obvious variability point in the water and sediment relationship between 1998 and 2017 and there is a certain stability in the overall runoff and sediment relationship; the synchronous frequency in the frequency of the combination of wet-normal-dry runoff and sediment is greater than that the asynchronous frequency during 1966-1990 and 1998-2017， the annual runoff and annual sediment transport in the previous period have a strong correlation at the annual sediment load is larger. The correlation between annual runoff and annual sediment transport in the latter period is stronger and the variation trend of annual runoff volume has similar variation tendency to the annual sediment.

Key words： runoff and sediment relationship; joint distribution; mutation diagnosis; encounter frequency; Toudaoguai Hydrological Station; Yellow River

1 引 言

随着黄河上游水利工程的运行和中游宁蒙河段灌区取用水等人类活动的影响，进入黄河中游的水沙过程发生了很大变化，对黄河中下游河道及水库冲淤、流域生态环境等产生了重要影响[1]。因此，科学揭示水沙关系变化规律对黄河中下游水资源管理和高效利用具有重要意义。

针对黄河流域水沙关系，有关学者开展了相关研究[2-4]。金鑫等基于水沙序列的理论频率曲线提出了黄河中游不同水文站的水沙频率组合划分标准[5];李新杰等从保证率的角度建立了潼关站1961—2018年58 a的年径流量和输沙量的频率曲线，并确定了潼关站来水来沙丰平枯的划分标准[6];马雁等基于黄河上游兰州站2014—2018年的水沙数据，总结了年径流量和年输沙量的关系和演变规律[7];考虑到环境变化和人类活动对流域来水来沙量的影响，李艳玲等结合滑动窗口和Copula函数，提出基于滑动Copula函数的降水和径流关系变异诊断法[8];郭爱军等提出滑动相关系数法用于泾河流域水沙关系的变异诊断，并基于Copula函数分析了径河流域的水沙关系演变特征[9];姚曼飞等基于泾河干支流8个水文站实测水沙数据，采用Copula函数构建了水沙联合分布模型，并计算了各个水文站的水沙丰平枯遭遇频率[10]。

鉴于头道拐站水沙关系对黄河中下游水沙调控的重要作用，以及已有研究多集中于径流量和输沙量特点或水沙关系单方面性质变化，对水沙组合遭遇情况分析稍有不足，笔者统计头道拐站1958—1990年和1998—2017年共计53 a的年径流量和年输沙量原始数据，通过建立水沙频率曲线，诊断水沙关系的变异特性，计算水沙丰平枯组合的遭遇频率，基于二维Copula函数建立二维水沙联合分布函数，分析黄河头道拐站水沙关系整体的变化情况及丰平枯遭遇规律，以期为流域水沙调控提供技术支撑。

2 研究数据与方法

2.1 研究数据

头道拐水文站位于内蒙古托克托县双河镇，是黄河上游的出口站，也是中游万家寨水库的入口站，其径流主要来自兰州站以上，泥沙主要来自兰州至头道拐区间支流，其水沙变化直接影响万家寨水库的水沙调度情况[11-12]。本研究选取头道拐水文站1958—1990年和1998—2017年两个时期的年径流量和年输沙量数据，资料来源于黄河流域水文年鉴。

2.2 研究方法

2.2.1 频率曲线

通过对年径流量和年输沙量序列的计算得到基本参数、CV、CS，进而确定参数α、β和b的值，即确定P-Ⅲ型分布函数。

本文运用适线法对频率曲线进行寻优，通过P-Ⅲ型频率分布建立年径流量和年输沙量的理论频率曲线，应用数学期望公式计算年径流量和年输沙量的经验频率，计算理论频率和经验频率拟合时的确定性系数R2，其计算公式如下[15]：

2.2.2 Copula函数

Copula函数是把随机变量X1、X2、…、XN的联合分布函数与各自的边缘分布函数U1、U2、…、UN相连接的连接函数，即函数C（u1，u2，…，uN）[16]。

2.2.3 Copula函数类型及参数估计

Copula函数在将边缘分布进行联合分布时包含了变量所有的相依信息，在建立联合分布函数的过程中保持信息的真实度[17]，更好地反映出水沙序列边缘分布之间的关系变化。Copula函数在总体上大致分为3种：正态型、t型和Archimedean型。在水文统计中，主要使用Archimedean型Copula函数对水沙序列进行联合分布，具体的表达式及参数范围见表1[17]。

2.2.4 Copula函数拟合优度检验

为了检验Copula函数对于水沙序列联合分布的拟合优度，引入经验Copula函数，比较经验累计频率与理论累计频率的拟合度。将样本值代入Copula频率公式计算出经验累计频率，同样将样本值代入3类Archimedean型Copula函数计算理论累计频率。计算确定性系数R2并进行比较，再根据离差平方和OLS最小准则与AIC信息准则做进一步的拟合优度检验[18]。

通过拟合优度检验选取最合适的Copula函数建立水沙序列的联合分布，从而得到接近实际值的理论分布。

2.2.5 变异诊断

本文基于Copula函数对水沙序列中水沙关系在时间分布上的变异情况进行诊断[21]。构造基于Copula函数的极大似然对数统计量公式如下：

原序列经过一次诊断后，若发现变异点则依据变异点划分为两个子序列，对子序列进行二次诊断，重复以上操作直至子序列的长度小于25。若原序列长度小于25，一次诊断即可。

对原水沙序列进行变异诊断是为了发现水沙序列在时间分布上是否存在平稳性，若存在，对原序列的水沙关系进行整体分析;若不存在，则根据变异点将原序列划分为若干个子序列，对每个子序列的水沙关系独立分析。

2.2.6 水沙丰平枯组合遭遇频率划分

在《水文基本术语和符号标准》[23]中，将河流的丰平枯年频率划分为5个级别，通过不同的保证率确定丰平枯年的频率划分标准，见表2[24]。

由于径流量和输沙量之间相依度高、相关性强，一般认为输沙量频率分布与径流量频率分布类似，因此输沙量的丰平枯年的频率划分也可以采用表2的标准[25]。通过建立满足P-Ⅲ型分布的年径流量和年输沙量频率分布，依据频率划分标准确定丰平枯年年径流量和年输沙量的划分标准，把年径流量和年输沙量均划分为5个级别，水沙丰平枯组合具体划分标准见表3。

3 数据分析

3.1 确定水沙频率曲线

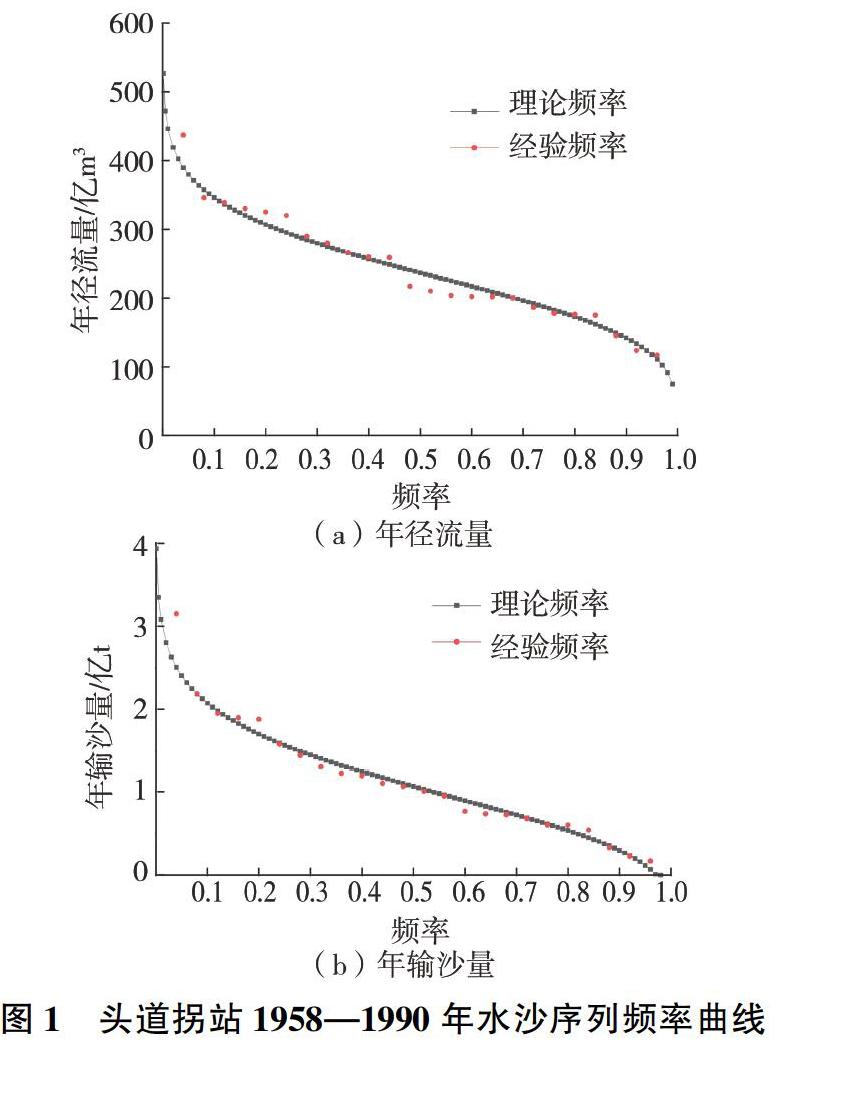
本文选取头道拐站1958—1990年和1998—2017年两个时段的年径流量和年输沙量序列，通过P-Ⅲ型分布函数建立年径流量和年输沙量序列的理论频率分布，同经验频率分布进行拟合，在满足确定性系数R2≥0.95的前提下，得到擬合度较高的年径流量和年输沙量的理论频率曲线，见图1和图2。两个时段年径流量和年输沙量频率变化情况见图3。

3.2 水沙联合分布及拟合优度检验

在确定合适的边缘分布后，作为变量输入Clayton、Gumbel和Frank Copula函数以及经验Copula函数，分别建立年径流量和年输沙量的联合分布与经验联合分布并进行拟合，根据确定性系数R2、OLS和AIC信息准则3个拟合优度检验指标选取最合适的Copula函数，3类Archimedean型Copula函数的参数及拟合优度检验值的计算结果见表4。

根据表4的检验值可知：1958—1990年的联合分布Clayton Copula的R2值最大、OLS和AIC的值均最小，即Clayton Copula的拟合优度最佳，表明Clayton Copula函数是用于头道拐站1958—1990年水沙联合分布最合适的Copula函数;1998—2017年的联合分布中Frank Copula的R2值最大、OLS和AIC的值均最小，说明Frank Copula的拟合优度最佳，明显优于其他两类，Frank Copula函数是用于头道拐站1998—2017年水沙联合分布最合适的Copula函数。

3.3 水沙关系的变异诊断

基于Gumbel Copula函数对1958—1990年和1998—2017年水沙关系进行变异诊断（一次诊断），见图4。

从图4中可知，两时段水沙关系的一次诊断中统计量Zn最大值（41.174 4）出现在1990年，在显著水平α为0.05时Zn远大于阈值（3.2），故存在变异点（1990年）。说明1958—1990年和1998—2017年两时段水沙关系存在差异。

分别基于Clayton Copula函数和Frank Copula函数对1958—1990年和1998—2017年年径流量和年输沙量关系进行变异诊断，见图5。

从图5中可知，在1958—1990年的一次诊断中统计量Zn最大值（5.933 7）出现在1965年，大于显著水平α=0.05时阈值（3.2），故1965年为变异点。在二次诊断中统计量Zn最大值（1.695 2）小于阈值，故1966—1990年水沙关系不存在变异点，具有一定的平稳性;在1998—2017年的一次诊断中统计量Zn最大值（0.203 9）小于阈值，因此认为在1998—2017年水沙关系不存在变异点，具有一定的平稳性。

头道拐1998—2017年水沙边缘分布的基于Frank Copula的联合分布如图8所示。从图8（a）中可见，1998—2017年水沙规律性较强，服从固定分布，年径流量和输沙量概率密度函数呈现尾部相关的特点，上尾部和下尾部相关性最强且具有对称性，表明年径流量的极大或极小值处对年输沙量有较大影响;从图8（b）中可见，Frank Copula的分布函数具有对称性，则水沙联合分布的累计频率具有对称性。

3.4 计算遭遇频率

根据建立的头道拐站年径流量和年输沙量的P-Ⅲ型频率分布，确定头道拐站水沙丰平枯组合中年径流量（X）和年输沙量（Y）的划分标准。选取1966—1990年和1998—2017年两段时期计算，这两段时期已被验证水沙关系存在一定的平稳性，见表5～表8。

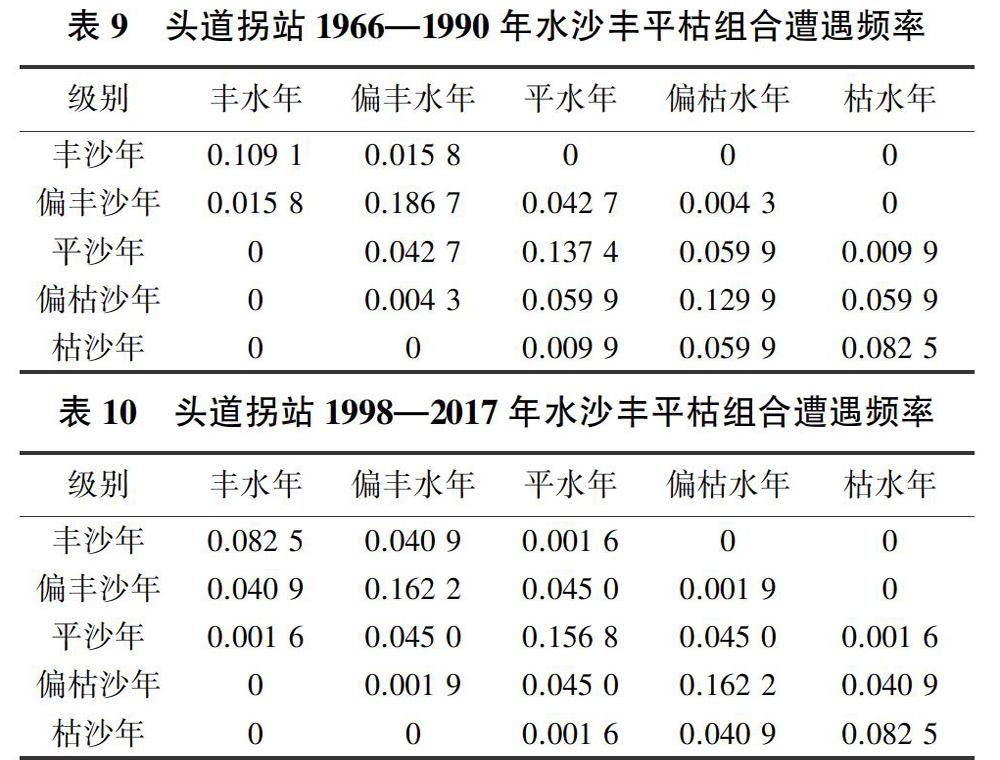
通过Clayton Copula建立水沙联合分布计算头道拐站1966—1990年水沙丰平枯组合遭遇频率，见表9。

由表9可知，头道拐站1966—1990年水沙丰平枯组合遭遇频率中，水沙同频组合（同丰、同偏丰、同平、同偏枯和同枯）频率总和为0.645 6，水沙异频组合频率为0.354 4，同频组合频率明显高于异频组合;水沙异频频率的高频部分主要集中于偏丰水平沙组合、平水偏丰沙组合、平水偏枯沙组合和偏枯水平沙组合，其频率均大于0.04;总体而言，同偏丰组合（0.186 7）最大，同平组合（0.137 4）次之，水沙丰枯相反组合的频率最小，说明头道拐站1966—1990年年径流量和年输沙量频率的关联性强，且在年径流量和年输沙量偏丰时关联性最强。

通过Frank Copula建立水沙联合分布计算头道拐站1998—2017年水沙丰平枯组合遭遇频率，见表10。由表10可知，头道拐站1998—2017年水沙丰平枯组合遭遇频率中，同频组合频率总和为0.646 1，异频组合频率总和为0.353 9，则同频组合频率明显高于异频频率;异频频率的高频部分主要集中于丰水偏丰沙组合、偏丰水丰沙组合、偏丰水平沙组合、平水偏丰沙组合、平水偏枯沙组合、偏枯水平沙组合、偏枯水枯沙组合和枯水偏枯沙组合，其频率均大于0.04;总体而言，同偏丰（同偏枯）组合（0.162 2）最大，同平组合（0.156 8）次之，水沙同丰（水沙同枯组）组合（0.082 5）第三，而枯水丰沙组合（丰水枯沙组合）最小，说明头道拐站1998—2017年年径流量和年输沙量频率的关联性强，水沙状态完全相反的组合的遭遇频率极小。

4 结 论

以头道拐站1958—1990年和1998—2017年两个时期的年径流量和年输沙量序列为研究对象，利用P-Ⅲ频率曲线探究水沙丰平枯组合遭遇频率，基于Copula函数构建二维水沙联合分布，分析水沙联合分布的累计频率，得到以下结论。

（1）头道拐站年径流量和年输沙量呈下降趋势，在1990年水沙关系发生变异。1958—1990年水沙序列中存在一个变异点（1965年），1966—1990年和1998—2017年序列水沙关系未发生明显变异，具有一定平稳性。

（2）由基于Copula建立的水沙联合分布的概率密度函数和分布函数可知，1958—1965年和1966—1990年水沙子序列概率密度函数上尾部相关性较强，即水沙序列中年径流量的较大值处变化趋势同年输沙量变化趋势关联性较强;1998—2017年水沙子序列的概率密度函數上尾部和下尾部相关性较强，即水沙序列中年径流量的高低变化趋势同年输沙量高低变化趋势关联性较强。

（3）由水沙丰平枯组合遭遇频率分析可得，在1966—1990年和1998—2017两个时段的水沙组合中水沙同频明显高于水沙异频，其中水沙异频组合发生的概率较小，头道拐站1966—1990年年径流量和年输沙量在平丰时相关性强，1998—2017年年径流量和年输沙量整体相关性较强，水沙丰平枯变化趋势基本一致。

参考文献：

[1] 胡春宏.黄河水沙变化与治理方略研究[J].水力发电学报，2016，35（10）：1-11.

[2] 赵阳，胡春宏，张晓明，等.近70年黄河流域水沙情势及其成因分析[J].农业工程学报，2018，34（21）：112-119.

[3] 高宗军，冯国平.黄河水沙变化趋势及成因分析[J].地下水，2020，42（1）：147-151.

[4] 高航，姚文艺，张晓华.黄河上中游近期水沙变化分析[J].华北水利水电学院学报，2009，30（5）：8-12.

[5] 金鑫，郝振纯，张金良.黄河中游水沙频率关系研究[J].泥沙研究，2006，31（3）：6-13.

[6] 李新杰，郜国明，朱亮，等.黄河潼关站水沙关系频率及协调度分析研究[J].人民黄河，2020，42（5）：47-51.

[7] 马雁，贾生海，张彦洪.黄河上游兰州水文站2004—2018年水沙特性分析[J].水利规划与设计，2020（4）：52-54，89.

[8] 李艳玲，畅建霞，黄强，等.基于滑动Copula函数的降水和径流关系变异诊断[J].水力发电学报，2014，33（6）：20-24，60.

[9] 郭爱军，黄强，畅建霞，等.基于Copula函数的泾河流域水沙关系演变特征分析[J].自然资源学报，2015，30（4）：673-683.

[10] 姚曼飞，党素珍，孟美丽，等.基于Copula函数的泾河流域水沙丰枯遭遇频率分析[J].水土保持研究，2019，26（1）：192-196，202.

[11] 冉大川，姚文艺，张攀，等.黄河头道拐站水沙来源空间分布及其影响因素[J].泥沙研究，2015，40（1）：42-48.

[12] 任智慧，王婷，曲少军.万家寨水库库区冲淤特点分析[C]//中国大坝工程学会.水库大坝高质量建设与绿色发展中国大坝工程学会2018学术年会论文集.北京：中国大坝工程学会，2018：172-177.

[13] 雷冠军，王文川，殷峻暹，等.P-Ⅲ型曲线参数估计方法研究综述[J].人民黄河，2017，39（10）：1-7.

[14] 黄继文.P-Ⅲ型分布频率分析在Excel中的实现及应用[J].水资源研究，2006，27（4）：7-9.

[15] 郭生练，叶守泽.论水文计算中的经验频率公式[J].武汉水利电力学院学报，1992，25（2）：38-45.

[16] PATTON A J. A Review of Copula Models for Economic Time Series[J].Journal of Multivariate Analysis，2012，110：4-18.

[17] 杜懿，麻荣永.不同Copula函数在洪水峰量联合分布中的应用比较[J].水力发电，2018，44（12）：24-26，58.

[18] 李天元，郭生练，罗启华，等.双参数Copula函数在洪水联合分布中的应用研究[J].水文，2011，31（5）：24-28，46.

[19] 贾玉红，宋松柏.陕北地区年降水量频率分布参数估算研究[J].水资源与水工程学报，2012，23（5）：48-50.

[20] 宋喜芳，李建平，胡希远.模型选择信息量准则AIC及其在方差分析中的应用[J].西北农林科技大学学报（自然科学版），2009，37（2）：88-92.

[21] HUANG S Z， LI P， HUANG Q， et al. Copula-Based Identification of the Non-Stationarity of the Relation Between Runoff and Sediment Load[J].International Journal of Sediment Research， 2017，32（2）：221-230.

[22] COSTA D A D. Copula Inference for Finance and Insurance[D].Zurich，Switzer-Land：ETH，2004：123-141.

[23] 中華人民共和国水利部.水文基本术语和符号标准：GB/T 50095—2014[S].北京：中国计划出版社，2014：2-51.

[24] 徐宇程，朱首贤，张文静，等.长江大通站径流量的丰平枯水年划分探讨[J].长江科学院院报，2018，35（6）：19-23.

[25] 林沫，刘颖，丛远飞，等.松辽流域主要河流水沙规律分析[J].东北水利水电，2009，27（12）：40-42，72.

【责任编辑 张 帅】