几何化在相对论解题中的应用

冯晓明，程敏熙

(华南师范大学 物理与电信工程学院 物理国家级实验教学示范中心， 广东 广州 510006)

在解答相对论题目的时候，往往需要进行大量的计算.尤其是关于参考系变换的题目，更为棘手，因为既要反复地运用洛伦兹变换，又要理顺思路，时刻区分清楚到底是“谁相对于谁在做什么”.并且很多计算得到的结论往往让人难以理解，似乎是“反直觉”的，违反人们的常识.

为简化计算的繁杂度，同时也为了更直观地解释结论，通常会设法把计算问题转化为闵可夫斯基空间中的几何问题，通过讨论几何图形的几何行为，求解题目的答案和结论.常见的几何化方法是二惯性系映射法[1]，其突出特点是无需移动事件点，仅通过映射的方法就能确定原事件点在新参考系中的坐标，快速而清晰，通常应用于快速解题；本文将提出另一种几何化方法，虽然相较于前者要移动事件点，但移动的依据即是时空间隔的不变性，能向初学者直观反映洛伦兹变换的动态过程以及时空间隔的不变性，传递物理学在变化中追求不变性的价值观.

以一道题目为例，一列车以速度V匀速向右运动，以地面为参考系，当列车头尾分别对准A、B时，A、B同时开枪，则同时死亡；若以列车为参考系，情况如何？

1 闵可夫斯基空间

在闵可夫斯基空间中，物理学中的事件概念就是实际事件的模型化，即认为每一事件发生在空间的一点和时间的一瞬，可用一个坐标(x,ct)表示.狭义相对性原理对时空变换的基本要求是保证时空间隔不变[2]，即

s′2=ct′2-x′2=

c2γ2(t-βx/c)2-γ2(x-βct)2=

(ct)2-x2=s2

(1)

这体现了物理学在变化中追求不变性的价值观.反映在空时图中，即要求事件点沿时空间隔等于常量的曲线上移动，这些曲线是以对角线为渐近线的两个双曲线族[3].其中，渐近线也被称为光锥，表示光相对于原点所有可能的位置的集合.当s2>0，称为类时间隔，当s2=0称为类光间隔，当s2<0，称为类空间隔.在类光与类时间隔中，均可以有因果关系，在变换后不能颠倒；而在类空间隔中，则不存在任何因果关系[4]，在变换后可以颠倒.由以上3种时空间隔可以划分为如图1所示的3种时空区.

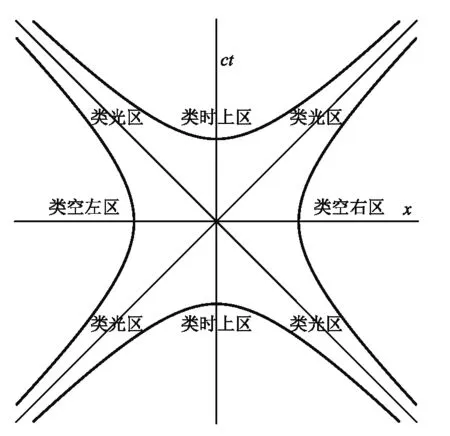
图1 时空区的划分

因为在空时图中，纵坐标是ct，横坐标是x，所以某两个事件点之间组成的直线斜率的绝对值表示速度大小的倒数[5]，这个速度的物理意义是两个事件点建立联系、进行信息交流的速度.而光速的斜率就是双曲线渐近线的斜率.

如果某两个事件点之间组成的斜率小于渐近线的速率，说明这两个事件点之间是超光速交流，因为狭义相对论要求实物粒子的速度不能大于真空中的光速[6]，所以这是不允许的.如果某两个事件点之间组成的斜率等于渐近线的速率，说明这两个事件点之间是等光速交流，除非它们之间是靠光信号交流，否则也是不允许的.如果某两个事件点之间组成的斜率大于渐近线的速率，说明这两个事件点之间是低光速交流，这是允许的.

2 二惯性系映射法

2.1 几何表示

以地面为参考系，如图2所示，点C为事件的中点，则A、B同时开枪、同时死亡.

图2 地面参考系

设A、B中点C为原点(0，0)，以地面为参考系建立ct-x空时图，追踪列车的中心，则列车初始事件也为(0，0)，再设其末事件为M(xM，tM).设A开枪为事件A1(xA1，tA1)，A死亡为事件A2(xA2，tA2)，B开枪为事件B1(xB1，tB1)，B死亡为事件B2(xB2，tB2)；在ct-x空时图中，因为直线斜率的绝对值表示速度倒数的大小，在一般情况下，列车的速度小于子弹的速度，则事件M的斜率大于事件B1与事件A2构成的斜率；经过一段时间后，如图3所示，其中，线段OM表示列车向右跑，线段A1B2表示A向左开枪打中B，线段B1A2表示B向右开枪打中A.

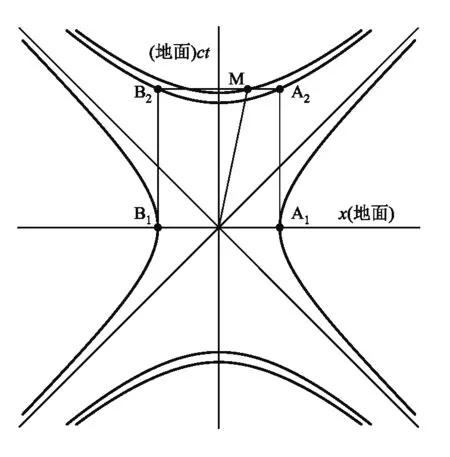
图3 地面ct-x空时图

若以列车为参考系，如图4所示，因为A开枪发出子弹的运动方向与列车的运动方向相反，而B开枪发出子弹的运动方向与列车的运动方向相同，说明A开枪发出的子弹与列车的相对速度大于B开枪发出的子弹与列车的相对速度，即前者的子弹比后者的子弹要先到达列车参考系下的事件中点C’则易知A比B先开枪，但不知A、B谁先死.

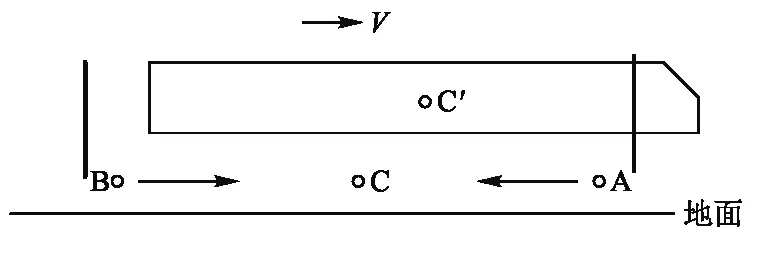
图4 列车参考系

对图3进行参考系变换，即从地面参考系变换到列车参考系，建立列车ct′-x′空时图，在列车参考系，则列车中心为原点(0，0)，设其末事件为M′(x′M，t′M)(因为此时列车相对于自己是静止的，没有发生位移)，设A开枪为事件A′1(x′A1，t′A1)，A死亡为事件A′2(x′A2，t′A2)，B开枪为事件B′1(x′B1，t′B1)，B死亡为事件B2′(x′B2，t′B2).因ct′轴与x′轴是关于光锥对称的，由此可确定x′轴的摆向，如图5所示.

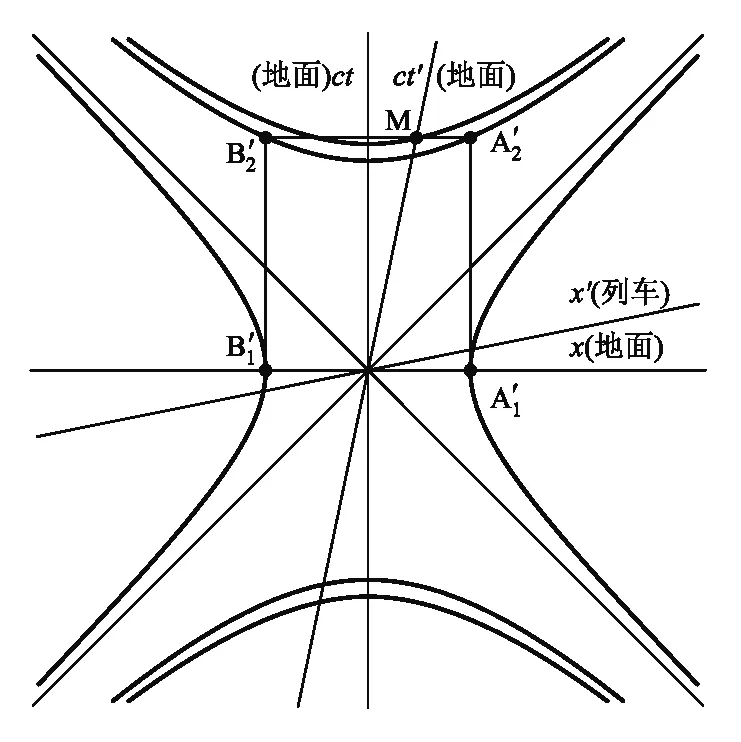
图5 时空轴关于光锥对称

2.2 映射规则

空时图中的映射规则是：从原事件点射出一条平行于x′轴的直线，其与ct′轴的交点即为这个事件点在新参考系中的时间坐标ct；同理，若从原事件点射出一条平行于ct′轴的直线，其与x′轴的交点即为这个事件点在新参考系中的空间坐标x.根据这一映射规则，所有事件点在新参考系中的时间坐标如图6所示，其直观而清晰地反映了4个事件发生的先后顺序，即依次为A开枪，B开枪，A死亡，B死亡.

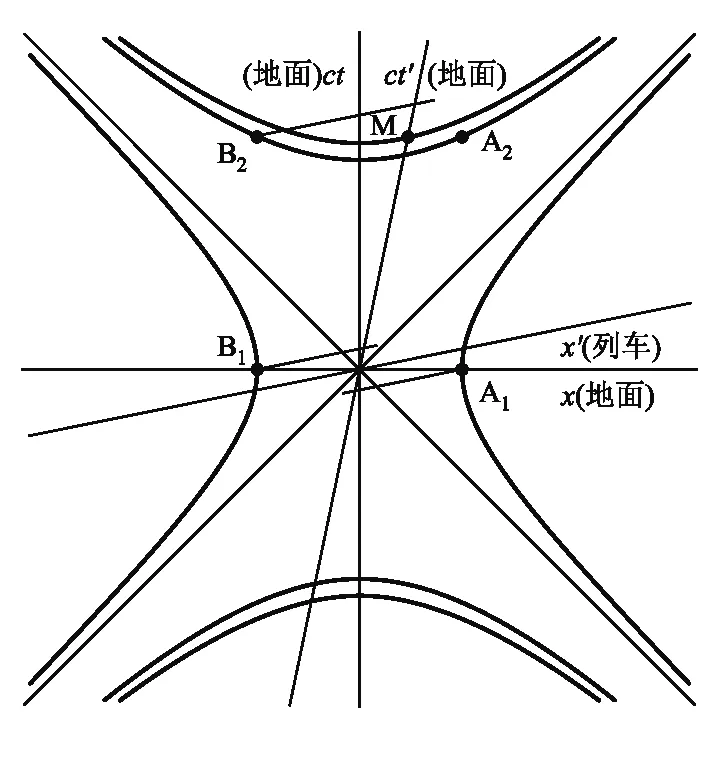
图6 映射

综上所述，二惯性系映射法具有步骤简单、快速直观的特点，非常适合于熟练者使用.然而，相对于初学者而言，可能存在以下两个困难.1) 不理解映射规则，仍然受制于定势思维，即认为原事件点分别在ct′轴与x′轴上的投影点才是其在新参考系中的时空坐标，则可能在映射过程中出错，若事件点的数量越多，则映射的难度就越大；2) 由于该方法不需要移动事件点，则较难体现洛伦兹变换的“动态”过程，也体现不出时空间隔的不变性，感受不到物理学在变化中追求不变性的价值观.而双曲旋转法能较好地照顾初学者的水平，有助于初学者解决上述两个困难.

3 双曲旋转法

3.1 旋转依据

双曲旋转法在变换前的步骤与二惯性系映射法完全一致，区别在于对图5的后续处理.因为在画图时总要先选一个惯性系作为标准，即把ct轴与x轴分别画成竖直与水平方向，而选哪个系作标准则完全任意[7]. 因此，若把列车参考系作为标准，则图5可以等效为图7.

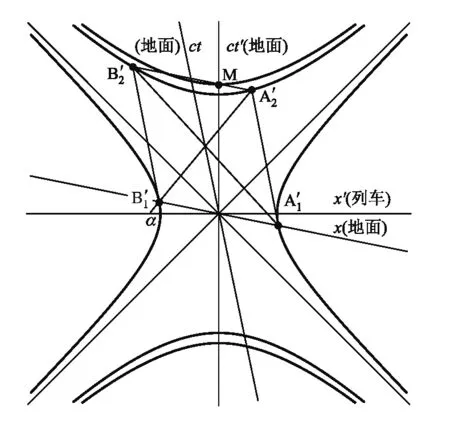
图7 双曲旋转

因为将两坐标轴的摆向仍旧转换为熟悉的正交关系，所以此举能较好地照顾了初学者的水平.此外，根据时空间隔不变性，所有事件点均沿其上的双曲线进行唯一方向的移动，此举既有利于初学者观察洛伦兹变换的动态过程，也有利于传递物理学追求不变性的价值观.这一价值观让物理学家格外关注不变性，在伽利略变换中，时间是不变的，所以体现了绝对时间的观念；而在洛伦兹变换中，时间却是可变的，所以体现了相对时间的观念；但在变化中却隐含着不变性，即时空间隔的不变性，从而构筑起四维时空.根据这一不变性，洛伦兹变换就能形象地描述为事件点沿双曲线的移动，把计算问题转化为几何问题.

设线段B′1A′2与x′轴正方向所成的角为α，因为这是定性分析，无法得知旋转角的具体大小，则事件B′1和事件A′2的时间先后关系有三种可能：1) 当旋转角度较小，即角α为锐角，则B′1早于A′2发生；2) 当旋转角度恰好，即角α等于0，则B′1和A′2同时发生；3) 当旋转角度较大，即角α为钝角，则B′1迟于A′2发生.

3.2 因果律制约

若想完全确定事件点，就必须考虑事件点之间的因果关系.

一开始，事件B′1的时间坐标小于事件A′2的时间坐标.经过参考系变换之后，虽然B开枪(即事件B′1)是沿着类空左区向左上移动，而A死亡(即事件A′2)是沿着类时上区向左下移动，此时事件B′1的时间坐标看似有可能大于事件A′2的时间坐标，但这是不可能的.因为还要考虑两个事件之间的交流速度是否超越了光速.

线段B′1A′2组成的斜率的绝对值表示子弹速度的倒数，因子弹的速度小于光速，所以线段B′1A′2组成的斜率应大于渐近线的斜率，即线段B′1A′2与x′轴正方向只能成锐角.所以事件B′1和事件A′2之间的时间关系只能是第一种可能，即B′1早于A′2发生.

这就意味着，在列车参考系中，A比B先开枪，A比B先死亡，且B开枪早于A死亡(因果律制约).这看起来似乎违反常识——先开枪的人怎么会先死亡呢？实际上，其中的因果关系并没有发生混乱.

虽然A先开枪，B后开枪，但这并不能保证B一定要先死亡，A一定要后死亡.因为在A开枪、B死亡、B开枪、A死亡这4个事件中，前两者有因果联系，后两者也有因果联系，其余的两两之间并无因果联系.即A开枪必然早于B死亡，B开枪必然早于A死亡，但B死亡与A死亡之间没有因果联系，不受因果律的制约，它们之间具体的先后发生顺序要由参考系变换后的图7决定，即B死亡迟于A死亡.由此可见，B死亡与A死亡所对应的事件点并不需要经过精确计算才能确定，而是能直接根据双曲线的走向来定性确定.

此外，A先开枪却先死亡，B后开枪却后死亡，可以推断出这么一个事实：从A发出的子弹速度是比从B发出的子弹速度要慢的.虽然是相同的子弹，但因为变换了参考系，所以速度大小会有所不同，并且可以肯定的是两者均不会超越光速.反映在图7上，则线段A′1B′2、线段B′1A′2、渐近线这三者的斜率绝对值必须是依次递减的，进一步定性确定4个事件点的相对位置.由此可见，对几何化结果的解读也能反过来调整事件点相对位置之间的合理性.

3.3 小结

对比参考系变换前后的图3和图7，可知4个事件点所构成的图形由矩形经过旋转拉伸后变为了平行四边形.根据双曲线的走向，先分别确定了B死亡与A先死亡的相对位置、B开枪与A开枪的相对位置；再根据线段A′1B′2、线段B′1A′2、渐近线之间斜率绝对值的大小关系，就能定性确定4个事件点之间的相对位置.几何化的结果十分直观地表达了4个事件之间发生的先后顺序，所以在列车参考系中，它们发生的先后顺序为A开枪，B开枪，A先死亡，B死亡.

4 拓展

几何化的方法还有助于对题目进行拓展，加深认识.例如，从图形的几何行为出发，除了旋转拉伸，还有对称.如果平行四边形在图7中关于ct′轴对称，所对应的情况即是在一列向左行驶的列车参考系中依次观察到B开枪，A开枪，B先死亡，A死亡，也得到了“谁先开枪谁先死”的结论.这说明在不同的参考系中，事件先后顺序在不违反因果律的前提下会发生不同的改变，这就是相对论时空观的神奇之处.此外，二惯性系映射法也能进行如上拓展.

5 结语

通过几何化方法，能将原本复杂的手动计算过程转化为简单直观的几何图形变形过程.常见的几何化方法是二惯性系映射法，其特点是只要根据对称性画出新参考系时空轴的摆向，就可无需移动事件点，仅在其原来的位置上通过映射规则确定在新参考系中的坐标，十分方便与快捷.

而双曲旋转法的特点是直观反映洛伦兹变换动态过程以及时空间隔的不变性，传递物理学在变化中追求不变性的价值观；通过对因果律的分析，能粗略确定参考系变换后事件点之间的相对位置；而对图形的解读既能反过来细调事件点之间的相对位置，互相牵制、互相印证；又能利用对称等几何性质对原题目进行适当拓展，加深理解.

综上所述，两种方法均有各自的特点，前者适合于熟练者快速地解题，后者适合于初学者的学习，共同目的均是把文本信息转化为图像信息，既提高了解题效率，又提升了“看图说话”的空间想象与几何分析能力.