致密砾岩储层岩石力学参数及地应力测井评价方法研究

王英伟,王林生,覃建华,李晓山,高阳,王硕

(1.中国石油新疆油田公司勘探开发研究院,新疆克拉玛依834000;2.中国石油新疆油田公司,新疆克拉玛依834000)

0 引 言

随着油田地质工程一体化勘探开发思想的普及,对油田地下储层岩石的评价工作已不仅仅局限于孔隙度、渗透率和饱和度等传统地质参数,而更多地关注到岩石弹性模量、强度和地应力等工程参数。储层岩石力学参数和地应力参数评价是油田经济高效开发的基础,也是井壁稳定分析、井眼轨迹优化、工程甜点评价与优选等油田勘探开发重要环节的关键[1-4]。

岩石力学参数主要包括岩石强度参数和弹性模量参数[5-6]。从参数的获取方式来说主要包括静态法和动态法2种。静态法是在实验室依据加载荷并测试加载过程中岩石应力、应变的变化来获取岩石力学参数,动态法是依据弹性波在岩石中的传播特性获取岩石力学参数[7-8],通常认为静态法更可靠。动态法的优势在于不损坏岩心且易与声波测井资料相结合,实现岩石力学参数连续评价。获取地应力的方法主要有水力压裂法、岩石声发射(凯瑟尔效应)[9-10]。这2种方法都可获取可靠的地应力,但都只能提供单点或者某一小段井眼的地应力,不适用于整个井段地应力剖面的建立[11-18]。

在实际油田储层岩石力学特性评价中,通常是基于测井资料中的纵波速度、横波速度和密度测井值,依据理论公式,计算目的层段岩石的力学参数和地应力[19-20]。对岩石结构较复杂、非均质性较强的致密砾岩储层,理论方法或仅依据实验数据的经验方法适用性有限[21-23]。本文将测井、岩石力学实验与水力压裂资料相结合,形成了一种有效的致密砾岩储层岩石力学参数和地应力参数评价方法。

1 致密砾岩储层岩石特征

1.1 致密砾岩储层岩石特征

研究区致密砾岩储层岩石的主要岩性为泥质含量较低的砂质细(小)砾岩和含砾中、粗砂岩。研究区岩石矿物种类主要为石英、钾长石、斜长石、方解石和黏土矿物,各矿物含量相对稳定,石英含量40%～50%、钾长石含量1%～4%、斜长石15%～22%、方解石含量0～13%、黏土矿物含量30%～40%。可见研究区致密砾岩储层岩石在岩石矿物成分上无明显差异。

从薄片分析资料可见,储层岩石颗粒粒径变化较大,大颗粒粒径可达小颗粒粒径数倍,储层岩石表现出较强的非均质性。镜下主要为砾状结构、砂砾状结构、含砾不等粒砂质结构,大颗粒形状以圆状、次圆状为主,中小颗粒形状以次棱角状、棱角状为主。胶结类型以压嵌型为主,分选性普遍较差。致密砾岩储层岩石孔隙分布相对均匀,储集空间以剩余粒间孔为主,粒内溶孔次之。部分岩心因粒间胶结物填充和大颗粒的影响,岩心较致密、孔隙体积较小。

采用气测法获取研究区致密砾岩储层基础物性参数,其密度变化范围为2.38～2.52 g/cm3,气测孔隙度变化范围为2%～12%,基础物性参数变化相对较大,反映出致密砾岩储层岩石物性较复杂。从岩心薄片观察和岩心基本物性参数分析可知,研究区砾岩储层表现出明显的致密特征,属于致密砾岩储层。

1.2 与其他致密油区块差异性分析

美国Bakken组和Eagle Ford组、中国延长7段、松辽白垩系等层组都发育有典型的致密油储层,这些储层普遍以砂岩、泥灰岩和粉细砂岩为主,物性普遍较差,多在15%以下,但表现出高含油特性,埋深相对较浅,普遍在3 300 m以上(见表1)。玛湖凹陷MD2井区致密砾岩储层与前述致密油储层相比,物性和含油性类似,埋深略深于前述储层,多在3 500 m以下。此外,研究区致密砾岩储层岩石中含有大量砾石且粒径差异较大,导致岩石的物理和力学性质受砾石含量、性质和分布等因素的影响,常规致密油储层中的岩石力学和地应力计算模型或经验公式不适用于该研究区。

表1 国内外典型致密油储层特征

2 岩石力学及地应力参数测井评价方法

2.1 岩石力学参数

测井岩石力学参数评价的理论依据来源于弹性波动理论,岩石弹性波速度与岩石的动态弹性参数相关,可由岩石波速获取其动态弹性参数。泊松比vd和动态弹性模量Ed分别为

(1)

(2)

式中,ρ为体积密度,g/cm3;Δts为纵波时差,μs/m;Δtp为横波时差,μs/m;d为动态参数;Ed为动态弹性模量,GPa。

岩石弹性参数计算主要是弹性模量和泊松比,其余参数可以基于这2个参数计算出来。考虑到部分井没有横波时差测井资料,在实际评价之前需建立纵波速度与横波速度之间的转换关系(见图1)。弹性波的传播特征与岩石的动力学特性有关,根据纵、横波速度与岩石动力学参数之间的理论关系,应用纵、横波时差及密度曲线计算岩石力学弹性参数。用声波测井资料计算的弹性模量是动态的,与岩石的静态力学性质之间有一定的差距,需要用实验室数据将动态参数转换成静态参数[23](见图2)。

图1 致密砾岩纵波速度和横波速度交会图

图2 致密砾岩泊松比、弹性模量动静态参数交会图

2.2 岩石强度参数

岩石强度参数指单轴抗压强度、抗拉强度、抗剪强度(内聚力和内摩擦角)等。单轴抗压强度是指岩石试件在单向受压至破坏时,单位面积上所能承受的荷载,简称抗压强度[24-25]。岩石的抗压强度可以通过单轴或三轴压缩试验得到,也可以根据测井资料计算得到

σc=Ed[0.008Vsh+0.0045(1-Vsh)]

(3)

C0=3.326×10-6σcKd

(4)

式中,σc为单轴抗压强度,MPa;C0为内聚力(岩石固有抗切强度)[26];Vsh为泥质含量,小数;Kd为动态体积模量,GPa。通过式(3)和式(4)计算的参数结果见图3。其中UCS为三轴压缩试验分析得到的单轴抗压强度,图3第2、第3道静态弹性模量和静态泊松比是基于动态弹性模量和动态泊松比,采用图2所示实验关系转换得到。岩石抗压强度和内聚力依据式(3)和式(4)得到,与岩心岩石力学实验分析结果对比可见计算结果可信。

2.3 孔隙压力

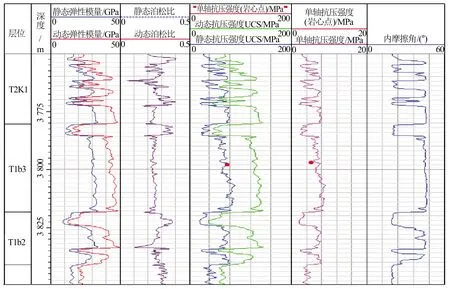
图3 M2井岩石强度参数计算结果

孔隙压力在岩石力学建模中占据非常重要的地位。上覆应力通过对地层密度进行积分计算得到[23]。孔隙压力与地应力大小是相互关联的,当深部存在异常高压地层时,3个主应力之间的差值会变小。区域构造应力为正断层和走滑断层机制时,最小水平主应力随孔隙压力的增加而增加。在走滑断层和逆断层机制下,由于高压,最大水平主应力的上限急剧减小。因此,不论是在正断层、走滑断层还是逆断层机制中,当孔隙压力接近上覆应力时,2个水平应力也一定会接近上覆地层压力[24]。计算出可靠的孔隙压力对于地应力大小计算至关重要。伊顿法是目前比较常用的一种预测地层压力的经验关系法,其原理是观察参数的实际值和正常压实趋势值的比率与地层孔隙压力的关系是由上覆压力梯度的变化决定的。该方法综合考虑了除压实作用以外其他高压形成机制作用,并总结和参考了钻井实测压力与各种测井信息之间的关系,其公式中的系数包含了压力形成的机制、超压保存的条件和砂泥岩之间的水动力学关系。其压力估算的基本形式为

pp=p0-(p0-pw)(Δtn/Δt)c

(5)

式中,pp为孔隙压力,MPa;p0为上覆地层压力,MPa;pw为地层水静液柱压力,MPa;Δt为观察点声波时差测井值,μs/ft[注]非法定计量单位,1 ft=12 in=0.304 8 m,下同;Δtn为正常压实趋势上的声波时差值,μs/ft;c为压实指数。实际计算中通过实验建立拟合规律来获取压实指数c等参数。

MD2区块中深部地层存在异常高压(地层压力系数1.58～1.66),异常高压的主要成因是快速沉积欠压实作用,导致生烃增压作用贡献小[27],所以采取适用于欠压实机理的伊顿方法进行MD2区块区域地层的孔隙压力预测。通过伊顿公式,按相同的伊顿指数,调整各井声波时差的正常压实趋势线(工区有统一的趋势线),多口井的趋势线与声波时差的相对关系保持一致,得到了多井的储层段地层孔隙压力剖面。用试油获得的地层压力数据进行标定,验证了孔隙压力剖面合理可靠。

通过试油测试得到了12口井的地层压力数据,与预测结果进行对比(见图4),平均相对误差仅为3.51%。由此可见,伊顿方法建立的地层孔隙压力模型预测结果精度较高,并且各井伊顿指数与趋势线保持一致,能够满足后续三维孔隙压力建模需求以及工程要求。

图4 孔隙压力实测值与计算值对比

2.4 地应力

给定深度处的最小水平主应力可以通过扩展的漏失试验、小型压裂或利用MDT、RFT工具直接测量得到,也可以通过差应变地应力实验获得[28]。但差应变测试只能通过岩心重复加载过程中的应变变化和弹性力学原理初步反映地应力大小,其结果的精确性受岩心保存状态等因素影响。通过测井资料可以计算出连续的地应力剖面数据,但是需要其中一种直接的方法进行标定,并结合成像测井等数据进行校核,多种方法综合分析地应力大小,有助于提高分析精度。最大、最小水平主应力可表示为

(6)

(7)

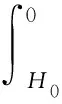
(8)

式中,Sh,min为最小水平主应力,MPa;SH,max为最大水平主应力,MPa;α为Biot系数;v为静态泊松比;E为静态弹性模量,MPa;εx、εy分别为最小、最大构造应力系数;Sv为垂向主应力,MPa;H0为测井起始点深度,m;ρ0(h)为未测井段深度为h点的密度;ρ(h)为深度为h点的测井密度;g为重力加速度,m/s2。采用前述公式实现测井地应力计算时,关键问题之一在于如何对计算结果进行标定。

方法1为利用实验室差应变岩心实验数据,来标定最大、最小水平主应力值;方法2为通过压裂分析得到的闭合应力,来标定最小水平主应力值。

方法1计算所得最大最小水平主应力值(见图5第3道),根据该实验测试结果对式(6)～式(8)计算的结果进行标定,可调整得到相应的构造应力系数(见表2)。

图5 利用测井资料计算得到M217井地应力剖面

表2 差应变试验测试点数据及对应构造应力系数

方法2利用研究区内9口井压裂施工数据得到的闭合压力来标定最小水平主应力值,对于最大水平主应力,则通过井眼稳定性分析,调整最大水平主应力,使计算得到的井眼破坏与井径观察基本一致,调整得到相应的构造应力系数(见表3)。由图5第3道可见,对地应力计算岩心标定方法的效果相对较差,与实际地层闭合应力不相符,导致这一现象的原因为致密砾岩地层岩石结构复杂,岩心分析与测井分析可能存在尺寸效应的影响。因此,方法2将测井资料直接与压裂施工数据相对应,更适用于致密砾岩地层。

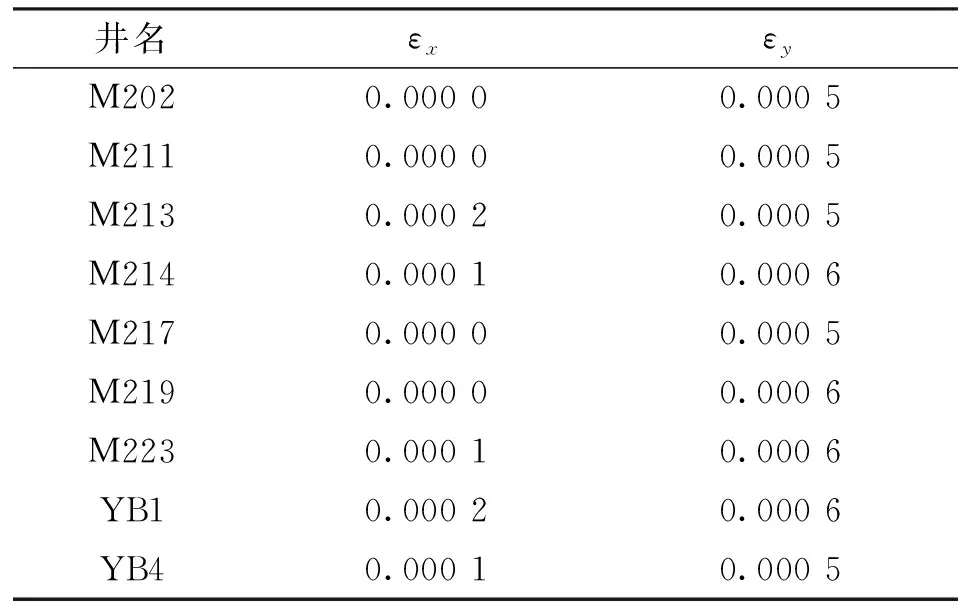
表3 方法2对应的构造应力系数

从地应力计算结果可见目的层的断层机制为正断层,与研究区地质认识基本一致。将计算得到的最小水平主应力与部分井压裂施工分析的闭合压力进行对比分析(见图6),平均相对误差率仅为1.38%,说明利用此模型能获取可信的最小水平主应力。

图6 计算最小水平主应力与闭合压力对比图

综上所述,该区块岩石力学实验室差应变实验获得的最大、最小水平主应力在实际应用中存在一定局限性,可能与岩心的储存条件和地层条件有差异等原因相关,如果采用此岩心试验点进行地应力的标定,存在一定不可靠风险,可能会导致计算结果出现偏差,甚至不符合区域地质背景。而压裂数据里获得的闭合压力相对更可靠,因此,有实测压裂数据时,应优先选取实测数据进行成果数据的标定,保证计算结果的可靠性。通过多种标定方法对比,最终获得了适用于研究区的可靠的最大、最小水平主应力计算模型。

3 结 论

(1)基于测井、实验、压裂施工资料形成了一套适用于致密砂砾储层的岩石力学参数和地应力计算模型,并通过实际井应用验证了模型的有效性。

(2)致密砾岩储层岩石孔隙度普遍较低,多小于10%,其动态弹性模量在15～40 GPa、动态泊松比在0.1～0.4。利用伊顿公式,通过多井声波时差趋势线对比以及部分井测试地层压力的标定,可获取可靠的致密砾岩储层岩石孔隙压力。

(3)受砾岩强非均质性的影响,依据岩心实验数据的常规地应力计算方法不适用于砾岩储层。通过将原有地应力计算模型与差应变实验、压裂分析相结合,实现了地应力大小定量标定,在此基础形成了可靠的地应力计算模型,较岩心标定方法更准确。