应用T-S模糊神经网络进行风电机组设备状态劣化分析的研究
国电电力河北新能源开发有限公司 张光军 孙立志
现阶段风电行业蓬勃发展,发展高峰期建设的大量风电场现已进入运维高压期,风力发电机造价高昂,维护工作重要性不言而喻。各发电企业深刻认识到风机运维工作紧急性,一方面采取定检定修运维方式保障常规维护,另一方面积极借助信息技术发展东风,采取智能化手段,向状态检修靠近,取得了一定成果。如王斐斐在《基于状态监测信息的风电机组齿轮箱故障预测研究》一文中阐述了应用改进灰色算法和时间序列法获取齿轮箱故障信息,取得预期效果。
T-S 模糊神经网络已广泛应用于各个行业故障预测类业务,本研究课题在各行业应用T-S 模糊神经网络算法的经验和总结基础上,结合风力发电特点,应用T-S 模糊神经网络算法进行风电机组设备状态劣化分析。
1 模糊控制基本原理
风机结构复杂,各大部件自成一体又相互影响,不同运行数据所占权重也很分散,造成评价结果水平不一。要在错综复杂的海量数据中准确识别个别数据在状态评判中所起作用和影响,应用模糊评判进行预测。应用多层评价的方法对风机劣化状态进行评价,该方法的算法思想是,首先对运行数据做低层次模糊综合评价,再对评价结果进行再评价,然后形成评价矩阵,再对评价矩阵做二次模糊综合评价,评价结果即为多层次评价结果。
以二级模糊综合评判为例,多级模糊综合评判分为几个步骤:首先将目标变量的影响因素按层级依次结构化,如将引起风机状态劣化因素集的风机大部件--齿轮箱类故障因素运行数据层级分为齿轮箱入口油温、齿轮箱轴承温度等更小的子影响因素;对子影响因素进行一级模糊评判,结合子因素集权重和隶属度矩阵得到单因素评判结果,再将单因素权重集和隶属度举证结合得到二级模糊评判结果。模糊神经网络算法核心在于权重系数和隶属函数的确定。
本研究课题状态劣化程度具有实时性,对应单一故障子影响因素出现程度和不同故障子因素在不同时间的隶属度由权重系数决定,这个系数不应该是固定的,故障因素间的相互影响关系也绝不是简单的线性关系,而根据故障影响因素分布关系的不同,其权重计算方式也不同。如呈指数分布权重计算ci=f(t)×ai=(1-e-kt)×ai,将由影响因素集合组成的矩阵做归一化处理,满足的ci即为最终所求权值向量。
对于模型隶属度的确定采取以下方法:首先采用专家知识并根据专家间水平和经验调整权重,解决隶属度计算的定性,再使用指派法确定隶属函数。根据故障影响因素自身属性的不同,模糊分布呈不同表现形式,如风机齿轮箱油温因素,其分布形式即为梯形分布,对质变现象做定性,当温度超出阈值上限将会出现故障。
神经网络和模糊控制的结合。神经网络算法具备优秀的学习能力,基于神经网络结构进行模糊推理可优化模糊推理的参数,方法的实现需先简化模糊推理形式。如多输入单输出模糊推理神经网络需三步实现:首先选取输入量并将输入量模糊化,再构造模糊规则表确定输出量对应的模糊关系[1],最后进行模糊判定,反模糊化输出量并输出最终结果。其中简化模糊推理形式构造神经网络实质上是实现输入变量到输出结果的非线性映射,映射过程采取多层前馈网络,应用误差反传算法,属于局部逼近网络。
2 具体实施方式
2.1 模糊变权部分
2.1.1 数据的获取
本文的数据获取,均通过实际的风机测点提取。数据结构如下:风力发电机组运行状态评价包括齿轮箱R1(齿轮箱油温R11、齿轮箱输入轴shaft1油温R12、齿轮箱输入轴shaft2油温R13、齿轮箱入口油温R14)、发电机系统R2(发电机组U 相绕组温度R21、发电机V 相绕组温度R22、发电机W 相绕组温度R23、发电机轴承a 温度R24、发电机轴承b 温度R25)、控制因素R3(发动机转速R31、有功功率R32、无功功率R33、电网电压R34)、机舱系统R4(偏航位置R41、机舱外温度R42、机舱温度R43)。
通过收集某风机上述相关数据,每个Rij标签还包括其二级子标签,例如有齿轮箱轴承温度、齿轮箱入口油温、齿轮箱油温、发电机轴承温度、发电机绕组温度、发电机冷却风温度等78个子标签,数据集大小为56G。以下列出齿轮箱和发电机系统1~20测点:齿轮箱轴承温度R111、齿轮箱入口油温R112、齿轮箱油温R113、发电机轴承温度R121、发电机绕组温度R122、发电机冷却风温度R123、发电机转速R124、电容器温度R131、变流器温度R132、塔顶控制柜温度R133、塔底柜温度R134、机舱位置R141、机舱震动R142、风速R211、环境温度R212、相电压R221、相电流R222、无功功率R223、有功功率R224、电网频率R225。
2.1.2 数据处理
由于每个测点海量数据存在参差不齐的问题,需将每个标签的数据量整理到相同的范围之内。对于缺值、少值问题本文采用平均值替代的方法进行数据的补充,对于某些元素的数据值范围过大的情况,选择采用min-max 标准化函数对数据进行归一化的处理。该函数输出值都在[0,1]之间。表达式 如 下:指标集R11=[]、R12=[]、R13=[]、R14=[],采 用matlab 中 的mapminmax 的数学公式为y=(ymax-ymin)×(x-xmin)/(xmax-xmin)+ymin,其中ymax及ymin分别为归一化区间,本程序中为[0,1]。
[xmin,xmax]为参数的最大值和最小值。目的是通过对数据的每一个维度的值进行重新调节(这些维度可能是相互独立的),这对后续工作十分重要,因为很多默认参数(如PCA-白化中的epsilon)都假定数据已被缩放到合理区间[2]。对此步骤输出数据数据计算劣化度。如发电机轴承温度数据分布符合梯形分布,计算方法如1和0分别表示劣化和正常。其中x 为实测值,[xmin,xmax]为参数的正常范围。评估指标常权值,以表1说明。
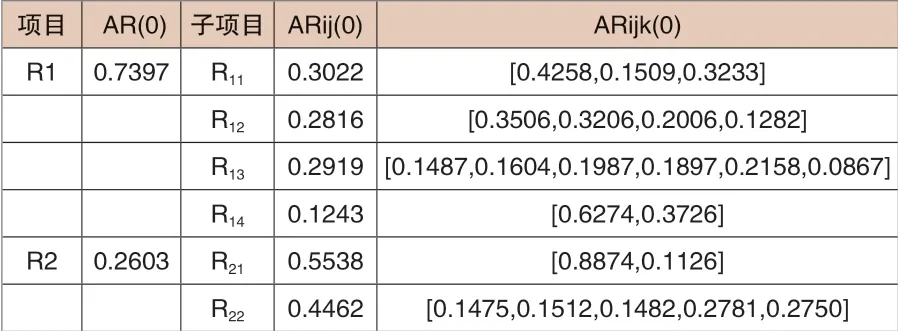
表1 齿轮箱和发电机部分评估结果
2.1.3 模型方法具体实现
应用上步实现的劣化度结果,结合专家知识,做隶属度计算。

用r11(g)、r12(g)、r13(g)、r14(g)依次表示当劣化度为g 时隶属度状态,分别为正常、良好、注意以及严重劣化。通过隶属度函数计算得到模糊关系矩阵R1,其中n 为单一评判单元个数,本研究课题中n=4,评判集矩阵为式(1),m 为评价指标数量。
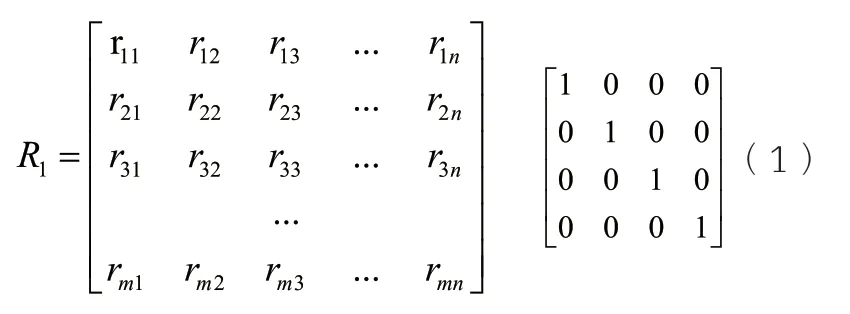
齿轮箱变权处理后权重为:AR11=[0.5656,0.0804,0.3540]、AR12=[0.3792,0.2426,0.16 61,0.2121]、AR13=[0.2448,0.1015,0.1692,0.2 609,0.1357,0.0879]、AR14=[0.7758,0.2242]、AR21=[0.9290,0.0710]、AR22=[0.1138,0.1314,0.124 9,0.4042,0.2258]。对齿轮箱R11运行状态进行评估:B11=AR1×VR11=[0.1267,0.7146,0.1588,0]。同 理可得其他评估指标评估结果,经整理得:

为增强多项指标发生严重偏移时变权算法的稳定性,当劣化度g>0.9时判定劣化状态为“严重”,停止后续计算;当劣化度<0.9时继续后续算法变权。只需要在第一级模糊评判时采用变权算法,之后的第二级和第三级直接应用给出的权重值。由一级模糊综合评判得到的各评估指标的评估结果,进行二级模糊综合评判,相应的权重为:
AR1(0)=[0.3022 0.2816 0.2919 0.1243]、AR2(0)=[0.3188 0.3806 0.1153 0.1923]。结合权重分配可得B1=AR1(0)×VR1=[0.4527 0.4649 0.0777 0]、B2=AR2(0)×VR2=[1.0000 0 0 0]。
采用二级模糊综合评判得到的各评估结果,进而得到三级模糊综合评估矩阵,相应权重为AR(0)=[0.7397 0.2603],结合权重分配可得[3]:B=AR
(0)×VR=[0.5952 0.3473 0.0575 0],基于最大隶属度原则,由bmax=b1=0.5952,可知状态评定为处于“良好”。
2.2 神经网络部分
采用四层神经网络结构,首末为输入输出层,中间层计算隶属度和变权值。
2.2.1 设计网络结构
每层都含有一个一维X 特征矩阵即为输入数据,一个二维W 权值矩阵,一个一维的误差矩阵error,同时该神经网络中还包含了一个一维的目标矩阵target,记录样本的真实类标。
X 特征矩阵:第一层隐含层特征矩阵长度比输入层输入数据的特征个数多1,隐含层的X 矩阵的长度比上一层多1,x[0]=1;W 权值矩阵:第一维长度设计为节点个数,第二维的长度比上一层节点多1;w[0][0]为该节点的偏置量;error 误差矩阵:数组长度设计为该层的节点个数;目标矩阵target:输出层的节点个数与其一致;激活函数:采用sigmoid 函数1/1+e-x。
2.2.2 神经网络的计算过程
按照以上的设计,向前传播得到下一层的输出结果如图1;求误差过程如图2;反向传播过程,调整权值,如图3。
向前传播得到下一层数据:向前传播的过程,即数据从输入层输入,经过隐含层,最后输出层的计算得到Y 值,Y 值为输出层的输出结果。输出矩阵即该层中所有节点(神经元)的输出值的集合。
求误差过程:根据样本的真实因变量,计算模型预测的结果与真实因变量的误差。然后将该误差反向传播到各个隐含层。误差从后往前传播。
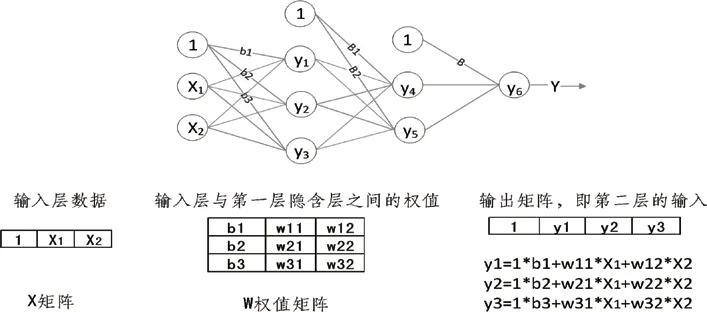
图1 下一层输出结果

图2 求误差过程
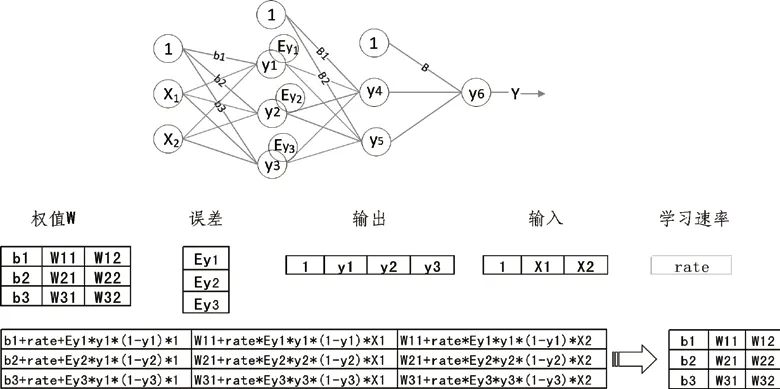
图3 反向传播过程,调整权值
反向传播过程调整权值:计算出各层的误差,再根据各层的误差,更新权重。新的权值计算方式如图3,依次更新输入层与第一层隐含层直接的权值、第一层隐含层与第二层隐含层之间的权值、第二层隐含层与输出层之间的权值。最终通过向前传播得到预测值。
评价模型结构:对单一评价指标进行劣化度和隶属度计算,将数据进行模糊化处理,对子影响因素进行一级模糊评判,结合子因素集权重和隶属度矩阵得到单一指标评判结果,再将单因素权重集和隶属度举证结合得到指标集综合评价结果。
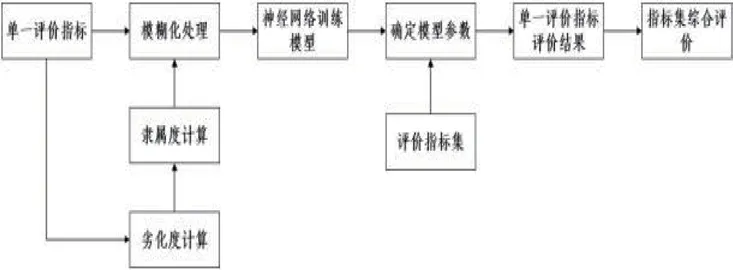
图4 T-S 模糊神经网络的综合评价模型
3 结果
此实验结果是结合子因素集权重和隶属度矩阵得到单因素评判结果,是为一级评判结果。以时间为轴表示出单因素状态优劣变化趋势。再将单因素权重集和隶属度矩阵结合得到二级模糊评判结果。根据二级模糊评判得分即可得出风机状态评语结果,实际应用时,可采取以时间维度根据得分用不同颜色柱状图表示风机状态变化过程。
综上,通过应用T-S 模糊神经网络算法对风机重要部件进行状态劣化评价,并用可视化方式展示,直观了解风机部件健康状态;应用部件运行状态数据,对风机整机运行状态进行指标集综合评价,用量化结果进行评价,以可视化方式展示,用以指导工作人员安排检修。

图5 风机部件评价具体实现结果

